Polarkoordinaten

Ein Polargitter verschiedener Winkel mit Grad-Angaben

In der Mathematik und Geodäsie versteht man unter einem Polarkoordinatensystem (auch: Kreiskoordinatensystem) ein zweidimensionales Koordinatensystem, in dem jeder Punkt in einer Ebene durch den Abstand von einem vorgegebenen festen Punkt und den Winkel zu einer festen Richtung festgelegt wird.

Der feste Punkt wird als Pol bezeichnet; er entspricht dem Ursprung bei einem kartesischen Koordinatensystem. Der vom Pol in der festgelegten Richtung ausgehende Strahl heißt Polarachse. Der Abstand vom Pol wird meist mit oder $\rho$ bezeichnet und heißt Radius oder Radialkoordinate, der Winkel wird mit $\varphi$ oder $\theta$ bezeichnet und heißt Winkelkoordinate, Polarwinkel, Azimut oder Argument.

Polarkoordinaten bilden einen Spezialfall von orthogonalen krummlinigen Koordinaten. Sie sind hilfreich, wenn sich das Verhältnis zwischen zwei Punkten leichter durch Winkel und Abstände beschreiben lässt, als dies mit - und -Koordinaten der Fall wäre. In der Geodäsie sind Polarkoordinaten die häufigste Methode zur Einmessung von Punkten (Polarmethode). In der Funknavigation wird das Prinzip oft als „Rho-Theta“ (für Distanz- und Richtungsmessung) bezeichnet.

In der Mathematik wird die Winkelkoordinate im mathematisch positiven Drehsinn (Gegenuhrzeigersinn) gemessen. Wird gleichzeitig ein kartesisches Koordinatensystem benutzt, so dient in der Regel dessen Koordinatenursprung als Pol und die -Achse als Polarachse. Die Winkelkoordinate wird also von der -Achse aus in Richtung der -Achse gemessen. In der Geodäsie und in der Navigation wird das Azimut von der Nordrichtung aus im Uhrzeigersinn gemessen.

Geschichte

Die Begriffe Winkel und Radius wurden bereits von den Menschen des Altertums im ersten Jahrtausend vor Christus verwendet. Der griechische Astronom Hipparchos (190–120 v. Chr.) erstellte eine Tafel von trigonometrischen Sehnenfunktionen, um die Länge der Sehne für die einzelnen Winkel zu finden. Mit Hilfe dieser Grundlage war es ihm möglich, die Polarkoordinaten zu nutzen, um damit die Position bestimmter Sterne festlegen zu können. Sein Werk umfasste jedoch nur einen Teil des Koordinatensystems.

In seiner Abhandlung Über Spiralen beschreibt Archimedes eine Spirallinie mit einer Funktion, deren Radius sich abhängig von seinem Winkel ändert. Die Arbeit des Griechen umfasste jedoch noch kein volles Koordinatensystem.

Es gibt verschiedene Beschreibungen, um das Polarkoordinatensystem als Teil eines formalen Koordinatensystems zu definieren. Die gesamte Historie zu diesem Thema wird in dem Buch Origin of Polar Coordinates (Ursprung der Polarkoordinaten) des Harvard-Professors Julian Coolidge zusammengefasst und erläutert. Demnach führten Grégoire de Saint-Vincent und Bonaventura Cavalieri diese Konzeption unabhängig voneinander in der Mitte des 17. Jahrhunderts ein. Saint-Vincent schrieb im Jahre 1625 auf privater Basis über dieses Thema und veröffentlichte seine Arbeit 1647, während Cavalieri seine Ausarbeitung 1635 veröffentlichte, wobei eine korrigierte Fassung 1653 erschien. Cavalieri benutzte Polarkoordinaten anfangs, um ein Problem in Bezug auf die Fläche der Archimedischen Spirale zu lösen. Etwas später verwendete Blaise Pascal Polarkoordinaten, um die Länge von parabolischen Winkeln zu berechnen.

In dem Werk Method of Fluxions (Fluxionsmethode) (geschrieben 1671, veröffentlicht 1736) betrachtet Sir Isaac Newton die Transformation zwischen Polarkoordinaten, auf die er sich als „Seventh Manner; For Spirals“, (Siebte Methode; Für Spiralen) bezog, und neun anderen Koordinatensystemen.

Es folgte Jacob Bernoulli, der in der Fachzeitschrift Acta Eruditorum (1691) ein System verwendete, das aus einer Geraden und einem Punkt auf dieser Geraden bestand, die er Polarachse bzw. Pol nannte. Die Koordinaten wurden darin durch den Abstand von dem Pol und dem Winkel zu der Polarachse festgelegt. Bernoullis Arbeit reichte bis zu der Formulierung des Krümmungskreises von Kurven, die er durch die genannten Koordinaten ausdrückte.

Der heute gebräuchliche Begriff Polarkoordinaten wurde von Gregorio Fontana schließlich eingeführt und in italienischen Schriften des 18. Jahrhunderts verwendet. Im Folgenden übernahm George Peacock im Jahre 1816 diese Bezeichnung in die englische Sprache, als er die Arbeit von Sylvestre Lacroix Differential and Integral Calculus (Differential und Integralberechnung) in seine Sprache übersetzte.

Alexis-Claude Clairaut hingegen war der erste, der über Polarkoordinaten in drei Dimensionen nachdachte, deren Entwicklung jedoch erst dem Schweizer Mathematiker Leonhard Euler gelang.

Polarkoordinaten in der Ebene: Kreiskoordinaten

Definition

Die Polarkoordinaten eines Punktes in der euklidischen Ebene (ebene Polarkoordinaten) werden in Bezug auf einen Koordinatenursprung (einen Punkt der Ebene) und eine Richtung (einen im Koordinatenursprung beginnenden Strahl) angegeben.

Das Polarkoordinatensystem ist dadurch eindeutig festgelegt, dass ein ausgezeichneter Punkt, auch Pol genannt, den Ursprung/Nullpunkt des Koordinatensystems bildet. Ferner wird ein von ihm ausgehender Strahl als sogenannte Polachse ausgezeichnet. Letztlich muss noch eine Richtung (von zwei möglichen), die senkrecht zu dieser Polachse ist, als positiv definiert werden, um den Drehsinn / die Drehrichtung / die Orientierung festzulegen. Nun lässt sich ein Winkel, der Polarwinkel, zwischen einem beliebigen Strahl, der durch den Pol geht, und dieser ausgezeichneten Polachse definieren. Er ist nur bis auf ganzzahlige Umdrehungen um den Pol eindeutig, unabhängig davon, was als Winkelmaß für ihn gewählt wird. Auf der Polachse selbst erfolgt noch eine beliebige, aber feste Skalierung, um die radiale Einheitslänge zu definieren. Nun kann jedem Paar $(r,\phi )\in \mathbb {R} _{0}^{+}\times \mathbb {R}$ ein Punkt der Ebene eindeutig zugeordnet werden, wobei man die erste Komponente als radiale Länge und die zweite als polaren Winkel ansieht. Solch ein Zahlenpaar bezeichnet man als (nicht notwendigerweise eindeutige) Polarkoordinaten eines Punktes in dieser Ebene.

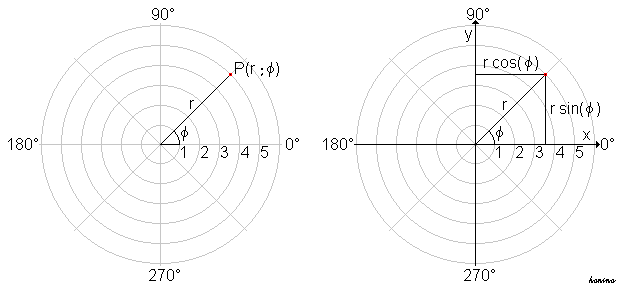
Ebene Polarkoordinaten (mit Winkelangaben in Grad) und ihre Transformation in kartesische Koordinaten

Die Koordinate , eine Länge, wird als Radius (in der Praxis auch als Abstand) und die Koordinate $\phi$ als (Polar)winkel oder, in der Praxis (gelegentlich) auch als Azimut bezeichnet.

In der Mathematik wird meistens der Winkel im Gegenuhrzeigersinn als positiv definiert, wenn man senkrecht von oben auf die Ebene (Uhr) schaut. Also geht die Drehrichtung von rechts nach oben (und weiter nach links). Als Winkelmaß wird dabei der Radiant als Winkeleinheit bevorzugt, weil es dann analytisch am elegantesten zu handhaben ist. Die Polarachse zeigt in grafischen Darstellungen des Koordinatensystems typischerweise nach rechts.

Umrechnung zwischen Polarkoordinaten und kartesischen Koordinaten

Umrechnung von Polarkoordinaten in kartesische Koordinaten

Wenn man ein kartesisches Koordinatensystem mit gleichem Ursprung wie das Polarkoordinatensystem, dabei die -Achse in der Richtung der Polarachse, und schließlich die positive -Achse in Richtung des positiven Drehsinnes wählt – wie in der Abbildung oben rechts dargestellt –, so ergibt sich für die kartesischen Koordinaten und eines Punktes:

$x=r\cos \varphi$

$y=r\sin \varphi$

Umrechnung von kartesischen Koordinaten in Polarkoordinaten

Die Umrechnung von kartesischen Koordinaten in Polarkoordinaten ist etwas schwieriger, weil man mathematisch gesehen dabei immer auf eine (nicht den gesamten Wertebereich des Vollwinkels umfassende) trigonometrische Umkehrfunktion angewiesen ist. Zunächst kann aber der Radius mit dem Satz des Pythagoras einfach wie folgt berechnet werden:

$r=\sqrt{x^2 + y^2}$

Bei der Bestimmung des Winkels $\varphi$ müssen zwei Besonderheiten der Polarkoordinaten berücksichtigt werden:

Für ist der Winkel $\varphi$ nicht eindeutig bestimmt, sondern könnte jeden beliebigen reellen Wert annehmen. Für eine eindeutige Transformationsvorschrift wird er häufig zu 0 definiert. Die nachfolgenden Formeln sind zur Vereinfachung ihrer Herleitung und Darstellung unter der Voraussetzung $r \ne 0$ angegeben.
Für $r \ne 0$ ist der Winkel $\varphi$ nur bis auf ganzzahlige Vielfache von $2\pi$ bestimmt, da die Winkel $\varphi$ und $\varphi + 2\pi k$ (für $k \in \Z$ ) den gleichen Punkt beschreiben. Zum Zwecke einer einfachen und eindeutigen Transformationsvorschrift wird der Winkel $\varphi$ auf ein halboffenes Intervall der Länge $2\pi$ beschränkt. Üblicherweise werden dazu je nach Anwendungsgebiet die Intervalle $(-\pi ,\pi ]$ oder $[0,2\pi)$ gewählt.

Für die Berechnung von $\varphi$ kann jede der Gleichungen

$\cos \varphi = \frac x r; \quad \sin \varphi = \frac y r; \quad \tan \varphi = \frac y x$

benutzt werden. Allerdings ist der Winkel dadurch nicht eindeutig bestimmt, auch nicht im Intervall $(-\pi ,\pi ]$ oder $[0,2\pi)$ , weil keine der drei Funktionen $\sin$ , $\cos$ und $\tan$ in diesen Intervallen injektiv ist. Die letzte Gleichung ist außerdem für x=0 nicht definiert. Deshalb ist eine Fallunterscheidung nötig, die davon abhängt, in welchem Quadranten sich der Punkt (x,y) befindet, das heißt von den Vorzeichen von und .

Berechnung des Winkels im Intervall (−π, π] bzw. (−180°,180°]

Mit Hilfe des Arkustangens kann $\varphi$ wie folgt im Intervall $(-\pi ,\pi ]$ bzw. $(-180^{\circ },180^{\circ }]$ bestimmt werden:

$\varphi ={\begin{cases}\arctan {\frac {y}{x}}&\mathrm {f{\ddot {u}}r} \ x>0\\\left(\arctan {\frac {y}{x}}\right)+\pi &\mathrm {f{\ddot {u}}r} \ x<0,\ y\geq 0\\\left(\arctan {\frac {y}{x}}\right)-\pi &\mathrm {f{\ddot {u}}r} \ x<0,\ y<0\\+\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y>0\\-\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y<0\\\end{cases}}$

Einige Programmiersprachen (so zuerst Fortran 77) und Anwendungsprogramme (etwa Microsoft Excel) bieten eine Arkustangens-Funktion $\operatorname {arctan2} (x,y)$ mit zwei Argumenten an, welche die dargestellten Fallunterscheidungen intern berücksichtigt und $\varphi$ für beliebige Werte von und berechnet.

Zum selben Ergebnis kommt man, wenn man den Punkt (x,y) in der kartesischen Ebene als komplexe Zahl $z=x+\mathrm {i} y$ auffasst und den Winkel

$\varphi =\arg(z)$

mittels der Argument-Funktion $\arg$ berechnet.

Mit Hilfe des Arkuskosinus kommt man mit nur zwei Fallunterscheidungen aus:

$\varphi = \begin{cases} +\arccos\frac{x}{r} & \mathrm{f\ddot ur}\ y\geq 0\\ -\arccos\frac{x}{r} & \mathrm{f\ddot ur}\ y<0 \end{cases}$

Durch Ausnutzen der Tatsache, dass in einem Kreis ein Mittelpunktswinkel stets doppelt so groß ist wie der zugehörige Umfangswinkel, kann das Argument $\varphi$ auch mit Hilfe der Arkustangens-Funktion mit weniger Fallunterscheidungen berechnet werden:

$\varphi ={\begin{cases}2\arctan {\frac {y}{r+x}}&{\mathrm {f{\ddot u}r}}\ r+x\neq 0\\\pi &{\mathrm {f{\ddot u}r}}\ r+x=0\end{cases}}$

Berechnung des Winkels im Intervall [0, 2π) bzw. [0, 360°)

Die Berechnung des Winkels $\varphi'$ im Intervall $[0,2\pi)$ bzw. $[0^\circ,360^\circ)$ kann im Prinzip so durchgeführt werden, dass der Winkel zunächst wie vorstehend beschrieben im Intervall $(-\pi ,\pi ]$ berechnet wird und, nur falls er negativ ist, noch um $2\pi$ vergrößert wird:

$\varphi' = \begin{cases} \varphi + 2\pi & \mathrm{falls}\ \varphi < 0\\ \varphi & \mathrm{sonst} \end{cases}$

Durch Abwandlung der ersten obenstehenden Formel kann $\varphi'$ wie folgt direkt im Intervall $[0,2\pi)$ bestimmt werden:

$\varphi '={\begin{cases}\arctan {\frac {y}{x}}&\mathrm {f{\ddot {u}}r} \ x>0,\ y\geq 0\\\arctan {\frac {y}{x}}+2\pi &\mathrm {f{\ddot {u}}r} \ x>0,\ y<0\\\arctan {\frac {y}{x}}+\pi &\mathrm {f{\ddot {u}}r} \ x<0\\\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y>0\\3\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y<0\\\end{cases}}$

Die Formel mit dem Arkuskosinus kommt auch in diesem Fall mit nur zwei Fallunterscheidungen aus:

$\varphi '={\begin{cases}\arccos {\frac {x}{r}}&\mathrm {f{\ddot {u}}r} \ y\geq 0\\2\pi -\arccos {\frac {x}{r}}&\mathrm {f{\ddot {u}}r} \ y<0\end{cases}}$

Verschiebung des Winkels

Bei geodätischen oder anderen Berechnungen können sich Azimute $\varphi$ mit Werten außerhalb des üblichen Intervalls $\varphi _{\text{min}}\leq \varphi <\varphi _{\text{min}}+2\pi$ mit der unteren Grenze $\varphi _{\text{min}}=0$ (oder auch $\varphi _{\text{min}}=-\pi$ ) ergeben. Die Gleichung

$\phi =\varphi -2\pi \cdot {\bigl \lfloor }{\frac {\varphi -\varphi _{\text{min}}}{2\pi }}{\bigr \rfloor }$

verschiebt $\varphi$ in das gewünschte Intervall, sodass also $\phi \in \left[\varphi _{\text{min}},\,\varphi _{\text{min}}+2\pi \right)$ gilt. Dabei ist $x\mapsto \lfloor x\rfloor$ die zur nächsten Ganzzahl abrundende Floor-Funktion, $\lfloor x\rfloor$ also für jedes reelle die größte ganze Zahl, die nicht größer als ist.

Funktionaldeterminante

Aus den Umrechnungsformeln von Polarkoordinaten in kartesische Koordinaten erhält man für die Funktionaldeterminante als Determinante der Jacobi-Matrix:

$\det J=\det {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \varphi }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2}\varphi +r\sin ^{2}\varphi =r$

Flächenelement

Flächenelement der Breite $r\cdot \mathrm {d} \varphi$ und der Höhe $\mathrm {d} r$ in Polarkoordinaten

Mit der Funktionaldeterminante ergibt sich für das Flächenelement in Polarkoordinaten:

$\mathrm dA = \mathrm dx\,\mathrm dy=|J|\,\mathrm dr\,\mathrm d\varphi = r\,\mathrm dr\,\mathrm d\varphi$

Wie das nebenstehende Bild zeigt, lässt sich das Flächenelement als ein differentielles Rechteck mit der Breite $r\cdot \mathrm {d} \varphi$ und der Höhe $\mathrm {d} r$ interpretieren.

Linienelement

Aus den obigen Transformationsgleichungen

$x=r \cos\varphi$

$y=r \sin\varphi$

folgen

$\mathrm dx= \cos\varphi \, \mathrm dr - r \, \sin\varphi \, \mathrm d\varphi$

$\mathrm dy= \sin\varphi \, \mathrm dr + r \, \cos\varphi \, \mathrm d\varphi$

Für das kartesische Linienelement gilt

$\mathrm ds^2=\mathrm dx^2+\mathrm dy^2\,$

wofür in Polarkoordinaten folgt:

$\mathrm ds^2=\mathrm dr^2+ r^2 \, \mathrm d\varphi^2$

Geschwindigkeit und Beschleunigung in Polarkoordinaten

Hierzu zerlegt man die Bewegung in eine radiale und eine dazu senkrechte „transversale“ Komponente. Für den Geschwindigkeitsvektor $\dot {\vec r}$ gilt

$\dot{\vec r}=\dot{r}\,\vec e_r + r\dot{\varphi}\,\vec e_\varphi$

mit den Einheitsvektoren $\vec e_r=(\cos(\varphi),\sin(\varphi))$ und $\vec e_\varphi=({-\sin(\varphi)},\cos(\varphi))$ .

Für die Beschleunigung $\ddot {\vec r}$ gilt

$\ddot{\vec r}=(\ddot r - r\dot\varphi^2) \,\vec e_r+(2\dot r \dot \varphi + r \ddot \varphi) \,\vec e_{\varphi}.$

Räumliche Polarkoordinaten: Zylinderkoordinaten und Kugelkoordinaten

Zylinderkoordinaten

Zylinderkoordinaten

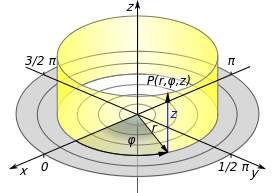
Zylinderkoordinaten oder zylindrische Koordinaten sind im Wesentlichen ebene Polarkoordinaten, die um eine dritte Koordinate ergänzt sind. Diese dritte Koordinate beschreibt die Höhe eines Punktes senkrecht über (oder unter) der Ebene des Polarkoordinatensystems und wird im Allgemeinen mit bezeichnet. Die Koordinate $\mathbf{\rho}$ beschreibt jetzt nicht mehr den Abstand eines Punktes vom Koordinatenursprung, sondern von der -Achse.

Umrechnung zwischen Zylinderkoordinaten und kartesischen Koordinaten

Wenn man ein kartesisches Koordinatensystem so ausrichtet, dass die -Achsen zusammenfallen, die -Achse in Richtung $\varphi =0$ zeigt und der Winkel $\varphi$ von der -Achse zur -Achse wächst (rechtsgerichtet ist), dann ergeben sich die folgenden Umrechnungsformeln:

$x=\rho\,\cos\varphi$

$y=\rho\,\sin\varphi$

$z=z$

Für die Umrechnung von kartesischen Koordinaten in Zylinderkoordinaten ergeben sich für $\rho$ und $\varphi$ die gleichen Formeln wie bei den Polarkoordinaten.

Basisvektoren

$\vec e_\rho = \frac{\frac{\partial \vec r}{\partial \rho}}{\left|\frac{\partial \vec r}{\partial \rho}\right|} = \begin{pmatrix} \cos\varphi \\ \sin\varphi \\ 0 \end{pmatrix},\quad \vec e_\varphi = \frac{\frac{\partial \vec r}{\partial \varphi}}{\left|\frac{\partial \vec r}{\partial \varphi}\right|} = \begin{pmatrix} -\sin\varphi \\ \cos\varphi \\ 0 \end{pmatrix},\quad \vec e_z = \frac{\frac{\partial \vec r}{\partial z}}{\left|\frac{\partial \vec r}{\partial z}\right|} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$

Die Basisvektoren $\vec e_\rho$ , $\vec e_\varphi$ und ${\vec {e}}_{z}$ sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.

Funktionaldeterminante

Die Hinzunahme der geradlinigen Koordinaten hat keinen Einfluss auf die Funktionaldeterminante:

$\det {\frac {\partial (x,y,z)}{\partial (\rho ,\varphi ,z)}}={\begin{vmatrix}\cos \varphi &-\rho \sin \varphi &0\\\sin \varphi &\rho \cos \varphi &0\\0&0&1\end{vmatrix}}=\rho$

Folglich ergibt sich für das Volumenelement $\mathrm {d} V$ :

$\mathrm{d}V=\rho \,\mathrm{d}\rho\, \mathrm{d}\varphi \, \mathrm{d}z$

Das entspricht auch der Quadratwurzel des Betrags der Determinante des metrischen Tensors, mit dessen Hilfe die Koordinatentransformation berechnet werden kann (siehe dazu Laplace-Beltrami-Operator).

${\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}={\begin{pmatrix}\cos \varphi &-\rho \sin \varphi &0\\\sin \varphi &\rho \cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}\mathrm {d} \rho \\\mathrm {d} \varphi \\\mathrm {d} z\end{pmatrix}}$

${\begin{pmatrix}\mathrm {d} \rho \\\mathrm {d} \varphi \\\mathrm {d} z\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}$

Vektoranalysis

Die folgenden Darstellungen des Nabla-Operators können in der gegebenen Form direkt auf skalare oder vektorwertige Felder in Zylinderkoordinaten angewendet werden. Man verfährt hierbei analog zur Vektoranalysis in kartesischen Koordinaten.

Gradient

Die Darstellung des Gradienten überträgt sich wie folgt von kartesischen in Zylinderkoordinaten:

$\nabla f={\frac {\partial f}{\partial \rho }}{\vec {e}}_{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\vec {e}}_{\varphi }+{\frac {\partial f}{\partial z}}{\vec {e}}_{z}$

Divergenz

Bei der Divergenz kommen noch weitere Terme hinzu, die sich aus den Ableitungen der von $\rho$ , $\varphi$ und abhängigen Einheitsvektoren ergeben:

$\nabla \cdot {\vec {A}}={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}(\rho A_{\rho })+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}$

Rotation

Die Darstellung der Rotation ist wie folgt:

$\nabla \times {\vec {A}}=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\vec {e}}_{\rho }+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\vec {e}}_{\varphi }+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}(\rho A_{\varphi })-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\vec {e}}_{z}$

Kugelkoordinaten

Kugelkoordinaten

→ Hauptartikel: Kugelkoordinaten

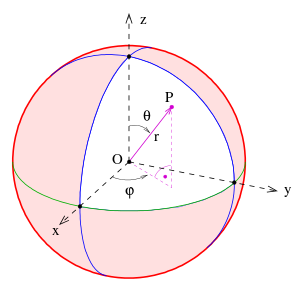
Kugelkoordinaten sind im Wesentlichen ebene Polarkoordinaten, die um eine dritte Koordinate ergänzt sind. Dies geschieht, indem man einen Winkel $\theta \in [0,\pi ]$ für die dritte Achse spezifiziert. Diese dritte Koordinate beschreibt den Winkel zwischen dem Vektor ${\vec {r}}$ zum Punkt und der -Achse. $\theta$ ist genau dann null, wenn in der -Achse liegt.

n-dimensionale Polarkoordinaten

Es lässt sich auch eine Verallgemeinerung der Polarkoordinaten mit $n \ge 3$ für einen -dimensionalen Raum mit kartesischen Koordinaten $x_{i}\in \mathbb {R}$ für $i=1,\dotsc ,n$ angeben. Dazu führt man für jede neue Dimension (induktiver Aufbau über selbige) einen weiteren Winkel $\vartheta_{n-2}\in [0,\pi]$ ein, der den Winkel zwischen dem Vektor $x\in \R^n$ und der neuen, positiven Koordinatenachse für $x_{n}$ angibt. Mit demselben Vorgehen kann in konsistenter Weise die Winkelkoordinate des 2-dimensionalen Raumes mittels $\varphi =\vartheta _{0}\in [0,\pi ]$ induktiv aus dem Zahlenstrahl konstruiert werden, sofern für die radiale Koordinate auch negative Werte, also somit ganz $\mathbb {R}$ , zugelassen wären.

Umrechnung in kartesische Koordinaten

Eine Umrechnungsvorschrift von diesen Koordinaten in kartesische Koordinaten wäre dann:

${\begin{array}{lcr}x_{1}&=&r\ \cos \varphi \ \sin \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{2}&=&r\ \sin \varphi \ \sin \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{3}&=&r\ \cos \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{4}&=&r\ \cos \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\\vdots &\vdots &\vdots \qquad \qquad \qquad \quad \\x_{n-1}&=&r\ \cos \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{n}&=&r\ \cos \vartheta _{n-2}\end{array}}$

Wie man nachweisen kann, gehen diese Polarkoordinaten für den Fall n=2 in die gewöhnlichen Polarkoordinaten und für n=3 in die Kugelkoordinaten über.

Funktionaldeterminante

Die Funktionaldeterminante der Transformation von Kugelkoordinaten in kartesische Koordinaten beträgt:

$\det {\frac {\partial (x_{1},\dotsc ,x_{n})}{\partial (r,\vartheta _{1},\dotsc ,\vartheta _{n-2},\varphi )}}=r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}$

Damit beträgt das -dimensionale Volumenelement:

${\begin{matrix}\mathrm {d} V&=&r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}\mathrm {d} r\ \mathrm {d} \varphi \ \mathrm {d} \vartheta _{1}\dotsm \mathrm {d} \vartheta _{n-2}\\&=&r^{n-1}\ \mathrm {d} r\ \mathrm {d} \varphi \ \prod \limits _{j=1}^{n-2}(\sin \vartheta _{j})^{j}\ \mathrm {d} \vartheta _{j}\end{matrix}}.$

Anmerkung: -dimensionale Zylinderkoordinaten sind einfach ein Produkt / eine Zusammensetzung -dimensionaler Kugelkoordinaten und (n-k) -dimensionaler kartesischer Koordinaten mit $k\geq 2$ und $n-k\geq 1$ .

Basierend auf einem Artikel in:

Wikipedia.de