
Spirale

Eine Spirale oder Schneckenlinie ist eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Betrachterperspektive von diesem Zentrum entfernt oder sich ihm annähert.
Spirale oder Schraube
Die Spirale wird manchmal mit der Schraube verwechselt. Während die prototypische Spirale ein Gebilde in der Ebene ist, wie zum Beispiel die Rille einer Schallplatte oder die Arme einer Spiralgalaxie, ist sowohl die Schraube als auch der Wendelbohrer ein räumliches Gebilde entlang des Hofes eines Zylinders. Auch die Abgrenzung zu einem Wirbelrad ist letztlich unklar.
Ebene Spiralen
Beschreibungen

Man kann Spiralen mathematisch am besten als Koordinatengleichungen im ebenen
Polarkoordinatensystem
beschreiben, wobei
als Funktion
von
dargestellt wird;
läuft im Allgemeinen bis unendlich anstatt nur bis 2π. Auch negative Winkel sind
möglich.
Polardarstellung einer Spirale:
In -
-Koordinaten
werden dadurch Punkte mit der Parameterdarstellung
beschrieben.
Ersetzt man in der Polardarstellung
durch
,
so wird die Spirale um den Winkel
gedreht. (Eventuell muss der Definitionsbereich angepasst werden.)
Beispiele
- Archimedische
Spirale:
- Hyperbolische
Spirale:
- Fermatsche
Spirale:
- Lituus-Spirale:
- Logarithmische
Spirale:
Die archimedische Spirale entsteht z.B. beim Aufwickeln eines
gleichmäßig dicken Teppichs. Sie wird in der -
-Ebene
durch eine Gerade beschrieben.
Die hyperbolische Spirale wird in der -
-Ebene
durch eine Hyperbel beschrieben. Sie entsteht bei der Zentralprojektion einer Schraubenlinie
auf eine zur Schraubachse senkrechte Ebene (siehe Bild). Man sieht sie
z.B. beim senkrechten
Blick durch eine Wendeltreppe
. Sie ist auch das Bild einer archimedischen
Spirale bei einer Kreisspiegelung
(Inversion).
Die Fermatsche Spirale heißt auch parabolische Spirale, da ihre Polargleichung eine Parabel beschreibt.
Die Lituus-Spirale ist das Bild einer fermatschen Spirale bei einer Kreisspiegelung.
Die logarithmische Spirale entsteht z.B. beim Wachstum von
Schneckenhäusern. Ihr Name rührt von der Auflösung ihrer Polargleichung
her:
.
-
 Hyperbolische Spirale:
Hyperbolische Spirale: -
 Fermatsche Spirale:
Fermatsche Spirale: -
 Lituus-Spirale:
Lituus-Spirale: -
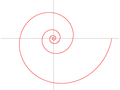 Logarithmische Spirale:
Logarithmische Spirale:
Neben diesen Spiralen gibt es noch welche, die nicht in dieses Konzept passen:
- Spirale des Theodorus. Sie ist keine glatte Kurve, sondern ein Polygon mit den Seitenlängen 1.
- Klothoide (Cornu-Spirale). Sie besitzt zwei asymptotische Punkte.
-
 Spirale des Theodorus
Spirale des Theodorus -
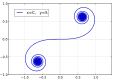 Cornu-Spirale
Cornu-Spirale
Eigenschaften
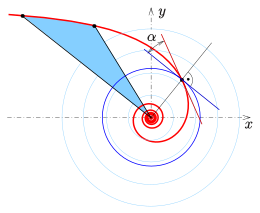
- Polarer Steigungswinkel
Der Winkel ,
unter dem die Spiraltangente den zugehörigen Polarkreis schneidet, heißt
polarer Steigungswinkel und
die polare Steigung. Aus der Formel
für den Tangentenvektor ergibt sich
Für eine Spirale mit der Gleichung
ist die polare Steigung
Für die archimedische Spirale ist
und damit
Für die logarithmische Spirale ist
konstant.
- Krümmung
Die Krümmung
einer Kurve in Polardarstellung ist
Für eine Spirale mit der Gleichung
ergibt sich
Z. B. ist für
(archimedische Spirale)
.
Die Spirale hat also keinen Wendepunkt.
Die Krümmung einer logarithmischen Spirale
ist
- Sektorfläche
Die Fläche eines Kurvensektors einer Kurve in Polardarstellung ist
Für eine Spirale mit der Gleichung
ergibt sich
Die Sektorfläche einer logarithmischen Spirale
ist
- Bogenlänge
Die Länge eines Bogens einer Kurve in Polardarstellung ist
Für eine Spirale mit der Gleichung
ergibt sich
Diese Integrale sind nicht mehr für alle
geschlossen lösbar. Im Fall der fermatschen Spirale ergibt sich ein elliptisches
Integral.
Die Bogenlänge einer logarithmischen Spirale
ist
Beschränkte Spiralen

Die Funktion
einer Spirale ist üblicherweise eine streng monotone, stetige Funktion und
unbeschränkt.
In den Standardbeispielen ist
eine Potenzfunktion oder eine Exponentialfunktion. Man kann allerdings für
auch eine beschränkte streng monotone Funktion wählen und erhält damit
dann eine beschränkte Spirale. Eine hierfür geeignete Funktion ist der Arkustangens:
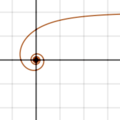
- Beispiel 1
Setzt man
und wählt
,
erhält man eine Spirale, die im Ursprung beginnt (wie die archimedische
Spirale) und sich dem Kreis mit Radius
annähert (im Bild links).
- Beispiel 2
Setzt man
und wählt
,
erhält man eine Spirale, die sich dem Ursprung nähert (wie die
hyperbolische Spirale) und sich dem Kreis mit Radius
annähert (im Bild rechts).
Räumliche Spiralen

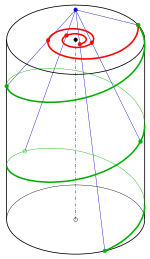
Konische Spiralen
Ist in der -
-Ebene
durch die Parameterdarstellung
eine ebene Spirale gegeben, so kann man eine dritte Koordinate
so anfügen, dass die dadurch entstehende räumliche Kurve auf dem senkrechten Kreiskegel
mit der Gleichung
liegt:
Spiralen dieser Art nennt man konische Spiralen. Sie waren auch schon Pappos bekannt.
- Beispiel
Geht man von einer archimedischen Spirale
aus, erhält man die konische Spirale (siehe Bild)
In diesem Fall kann man die konische Spirale auch als Schnittkurve eines Kegels und einer Wendelfläche auffassen.

Kugelspiralen
Stellt man eine Kugel mit Radius
in Kugelkoordinaten dar:
und gibt eine lineare Abhängigkeit der Winkel
vor, so erhält man eine Kugelspirale mit der
Parameterdarstellung
Auch Kugelspiralen wurden schon von Pappus untersucht. Sie sind spezielle Clelia-Kurven.
Lässt man
also
zu, erhält man eine vivianische
Kurve.
Man beachte: Eine Loxodrome ist keine Kugelspirale in dem hier erklärten Sinne.
-
 Kugelspirale
Kugelspirale -
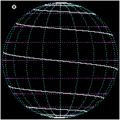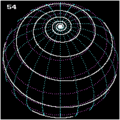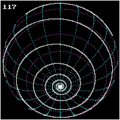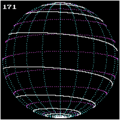 Loxodrome
Loxodrome
In der Natur


Viele Pflanzen und manche Tiere weisen in ihrem Bauplan spiralige Strukturen auf wie zum Beispiel das Schneckenhaus. Fossile Beispiele sind die Ammoniten. Die „Anordnung“ dieser biologisch erzeugten Spiralen, die meistens auf logarithmischen Spiralen beruhen, erfolgt wiederum in den allermeisten Fällen als Fibonacci-Folge.
In der Physik vollführt ein elektrisch geladenes Teilchen, das sich in einem Magnetfeld bewegt, eine Spiralbahn. Voraussetzung ist, dass sich das Teilchen nicht parallel, antiparallel oder quer zur Nord-Süd-Ausrichtung des Magnetfeldes bewegt. Die Kraft, die das Teilchen auf eine spiralförmige Bahn zwingt, heißt Lorentzkraft. Streng genommen ist diese Flugbahn aber eine Schraubenlinie. Bei der Bewegung parallel oder antiparallel zur Nord-Süd-Ausrichtung des Magnetfeldes entsteht eine gerade Flugbahn, und bei der Bewegung quer zur Nord-Süd-Ausrichtung des Magnetfeldes entsteht eine Kreisbahn. Wenn ein elektrisch geladenes Teilchen auf einer solchen Kreisbahn Energie durch elektromagnetische Strahlung abgibt, dann bewegt es sich auf einer immer enger werdenden Spiralbahn. Die schraubenförmige Flugbahn des elektrisch geladenen Teilchens ist eine Überlagerung einer geraden Flugbahn, und einer Kreisbahn. Bei Energieverlusten durch elektromagnetische Strahlung, und auch in inhomogenen Magnetfeldern, entstehen konische Spiralen aus der Überlagerung von Schraube und Spirale.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.01. 2023