
Monotone reelle Funktion
.png)
Eine monotone reelle Funktion ist eine reellwertige
Funktion einer reellen Variablen, bei der der Funktionswert
entweder immer wächst oder immer fällt, wenn das Argument
erhöht wird. Steigt der Funktionswert immer, wenn das Argument erhöht wird, so
heißt die Funktion streng monoton steigend, steigt der Funktionswert
immer oder bleibt er gleich, heißt sie monoton steigend. Analog heißt
eine Funktion streng monoton fallend, wenn ihr Funktionswert immer fällt,
wenn das Argument erhöht wird, und monoton fallend, wenn er immer fällt
oder gleich bleibt. Reelle monotone Funktionen sind klassische Beispiele für monotone
Abbildungen.
Definition
Eine Funktion ,
wobei
eine Teilmenge von
ist, heißt
- monoton steigend, wenn für alle
mit
gilt, dass
.
- streng monoton steigend, wenn für alle
mit
gilt, dass
.
- monoton fallend, wenn für alle
mit
gilt, dass
.
- streng monoton fallend, wenn für alle
mit
gilt, dass
.
- monoton, wenn sie entweder monoton steigt oder monoton fällt.
- streng monoton, wenn sie entweder streng monoton steigt oder streng monoton fällt.
Manchmal werden die nicht strengen Monotoniebegriffe auch für
definiert. Die beiden Definitionen sind gleichwertig. Synonym für „streng“
findet man auch „strikt“, monoton fallend wird gelegentlich auch antiton
genannt, genauso wie monoton wachsend auch isoton genannt wird. Es findet
sich auch die Bezeichnung „wachsend“ anstelle von „steigend“.
Beispiele
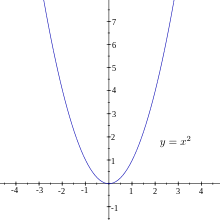
- Die Funktion
ist auf
streng monoton fallend. Ist nämlich
, so ist
und
. Die Bedingung, dass
sein soll, ist äquivalent zu
. Es ist aber mit der dritten binomischen Formel
,
- also ist
streng monoton fallend auf
. Der Nachweis, dass
streng monoton wachsend auf
ist, funktioniert analog, aber mit dem Argument, dass
wenn
ist. Damit ist die Funktion aber nicht monoton auf
, da sie auf diesem Intervall kein festes Monotonieverhalten besitzt.
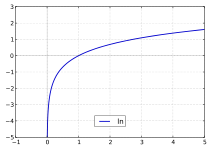
- Der Logarithmus
ist streng monoton wachsend auf
.
ist wieder äquivalent zu
. Dann ist
,
- wenn
, da dann
ist und dementsprechend
. Also ist
. Somit ist der Logarithmus streng monoton wachsend und demnach auch streng monoton.
- Die Funktion
- ist monoton fallend auf dem Intervall
, aber nicht streng monoton fallend. Der Nachweis der Monotonie in der linken Hälfte des Intervalls folgt dem ersten Beispiel, auf dem Intervall
ist jedoch
und damit kann keine strikte Monotonie gelten. Somit ist die Funktion monoton fallend und damit auch monoton.
Eigenschaften
Für eine reelle monotone Funktion
mit
gilt:
- Streng monotone Funktionen sind stets injektiv,
sie nehmen also jeden Wert nur höchstens einmal an. Ist
streng monoton und
ein Intervall und
die Bildmenge, so ist
bijektiv. Daher existiert für streng monotone Funktionen auch immer die Umkehrfunktion. Beispielsweise ist die Sinusfunktion auf dem Intervall
streng monoton wachsend. Schränkt man die Bildmenge auf das Intervall
ein, so ist sie bijektiv und damit invertierbar. Die Umkehrfunktion ist dann der Arkussinus
.
- Sie hat in jedem Häufungspunkt
ihres Definitionsbereichs
einen linksseitigen und rechtsseitigen Grenzwert.
- Sie kann nur Sprungstellen als Unstetigkeitsstellen haben.
- Die Menge der Sprungstellen in ihrem Definitionsbereich ist abzählbar, muss aber nicht notwendigerweise endlich sein.
- Sie ist fast überall
differenzierbar,
d.h. die Menge der Stellen, an denen
nicht differenzierbar ist, bildet eine lebesguesche Nullmenge.
- Eine im Intervall
definierte monotone Funktion ist dort Riemann-integrierbar.
- Für jede monoton wachsende Funktion gilt
für beliebige
. Diese Eigenschaft nutzt man teilweise, um die Monotonie zu verallgemeinern, siehe letzter Abschnitt.
- Die Monotonie reeller Funktionen ist ein Spezialfall einer monotonen
Abbildung. Im Falle einer monoton fallenden Funktion sind die sind beiden
geordneten Mengen dann
und
, die Abbildung ist die Funktion
.
Ableitungen als Monotoniekriterium
Kriterien
Ist die Funktion
differenzierbar, so lässt sich die Ableitung als Monotoniekriterium verwenden.
Die Kriterien für strenge Monotonie lauten:
- Ist
für alle
, so wächst
in
streng monoton.
- Ist
für alle
, so fällt
in
streng monoton.
Zu beachten ist, dass dieses Kriterium nur hinreichend, aber nicht notwendig ist. Es gibt auch streng monotone Funktionen, deren Ableitung null wird, ein Beispiel ist weiter unten aufgeführt. Es lässt sich mit zusätzlichen Forderungen noch eine Verschärfung dieser Kriterien formulieren:
- Es ist
(
) für alle
und die Ableitung ist auf keinem echten Teilintervall konstant gleich null (wobei ein echtes Intervall ein Intervall mit mehr als einem Element ist) genau dann, wenn
streng monoton wachsend (streng monoton fallend) ist.
Die Kriterien für Monotonie lauten:
für alle
genau dann, wenn
in
monoton wächst.
für alle
genau dann, wenn
in
monoton fällt.
Bei diesen Kriterien handelt es sich um Äquivalenzen.
Alle genannten Kriterien lassen sich noch erweitern: Ist zusätzlich
stetig auf
(bzw.
oder
),
so gilt die Aussage über die Monotonie auch für das Intervall
(bzw.
oder
).
Beispiele
- Für die Exponentialfunktion
ist
für alle
. Also ist sie streng monoton wachsend.
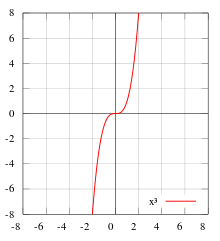
- Die Funktion
besitzt die Ableitung
, diese wird bei
null. Aber die Funktion ist streng monoton wachsend. Ist nämlich
und haben
dasselbe Vorzeichen, so ist
.
- Haben beide unterschiedliches Vorzeichen, so ist direkt
. Somit ist dies ein Beispiel dafür, dass die ersten beiden Kriterien nur hinreichend, aber nicht notwendig sind. Das dritte Kriterium greift hier aber: Die Ableitung der Funktion verschwindet bloß im Punkt
und ist sonst größergleich null. Dies ist äquivalent zum monotonen Wachstum von
.
Umkehrfunktion
Sei
ein Intervall und
sei streng monoton wachsend/fallend und stetig. Dann ist:
- die Bildmenge
ein Intervall,
bijektiv,
- die Umkehrfunktion
streng monoton wachsend/fallend und stetig,
, wenn wachsend und
, wenn fallend.
Verallgemeinerungen
K-monotone Funktionen
Verallgemeinert man den Monotoniebegriff für Funktionen ,
so definiert man auf dem
einen echten
Kegel
und betrachtet die von ihm definierte verallgemeinerte
Ungleichung
und die strikte verallgemeinerte Ungleichung
sowie eine konvexe Menge
.
Dann heißt eine Funktion
- K-monoton wachsend (K-monoton fallend) wenn für alle
mit
gilt, dass
(bzw.
)
- strikt K-monoton wachsend (strikt K-monoton fallend) wenn
für alle
gilt, dass
(bzw.
) ist.
Wählt man als Vektorraum den
(den Raum aller reellen symmetrischen Matrizen) und als Kegel den semidefiniten Kegel
(bzw. als verallgemeinerte Ungleichung die Loewner-Halbordnung),
so erhält man die Matrix-monotonen
Funktionen.
Monotone Funktionen zwischen Vektorräumen gleicher Dimension
Eine Möglichkeit, Monotonie für Funktionen
zu verallgemeinern ist, für
zu fordern, dass wenn
für
ist, dass dann für eine monoton wachsende Funktion gelten soll, dass
ist. Die Formulierung monoton fallender Funktionen und der strikten Versionen
folgt analog. Dieses Vorgehen entspricht der Verallgemeinerung der Ordnung auf
auf die komponentenweise Halbordnung auf
.
Alternativ kann man die Eigenschaft von monoton wachsenden reellen
Funktionen, dass für beliebige
gilt, dass
ist verallgemeinern. Dies führt dann zu dem folgenden Monotoniebegriff: gegeben
sei
und eine Funktion
.
Die Funktion heißt
- Monoton auf
, wenn
für alle
gilt.
- Strikt monoton auf
, wenn
für alle
gilt.
- Gleichmäßig monoton auf
, wenn
für alle
mit
gilt.
Verallgemeinert man dies weiter, so erhält man den Begriff eines monotonen Operators.
Monotonie über den Differenz-Operator (Rechtecksmonotone Funktion)
Die Monotonie für Funktionen
kann auch über den Differenz-Operator
definiert werden. Funktion wird dann eine rechtecksmonotone Funktion genannt, wenn
gilt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.03. 2020