Riemannsches Integral
Das Riemannsche Integral (auch Riemann-Integral) ist eine nach
dem deutschen Mathematiker
Bernhard
Riemann benannte Methode zur Präzisierung der anschaulichen Vorstellung des
Flächeninhaltes zwischen der -Achse
und dem Graphen
einer Funktion.
Der riemannsche Integralbegriff gehört neben dem allgemeineren lebesgueschen zu den
beiden klassischen der Analysis. In vielen Anwendungen werden nur Integrale von stetigen
oder stückweise stetigen Funktionen benötigt. Dann genügt der etwas einfachere,
aber weniger allgemeine Begriff des Integrals von Regelfunktionen.
Das dem Riemannschen Integral zu Grunde liegende Konzept besteht darin, den
gesuchten Flächeninhalt mit Hilfe des leicht zu berechnenden Flächeninhalts von
Rechtecken anzunähern. Man geht dabei so vor, dass man in jedem Schritt zwei
Familien von Rechtecken so wählt, dass der Graph der Funktion „zwischen“ ihnen
liegt. Indem man sukzessive die Anzahl der Rechtecke erhöht, erhält man mit der
Zeit eine immer genauere Annäherung des Funktionsgraphen durch die zu den
Rechtecken gehörenden Treppenfunktionen.
Entsprechend lässt sich der Flächeninhalt zwischen dem Graphen und der
-Achse
durch die Flächeninhalte der Rechtecke approximieren.
Definitionen
Es gibt im Wesentlichen zwei gängige Verfahren zur Definition des Riemann-Integrals:
- das Jean Gaston Darboux zugeschriebene Verfahren mittels Ober- und Untersummen und
- Riemanns ursprüngliches Verfahren mittels Riemann-Summen.
Die beiden Definitionen sind äquivalent: Jede Funktion ist genau dann im darbouxschen Sinne integrierbar, wenn sie im riemannschen Sinne integrierbar ist; in diesem Fall stimmen die Werte der beiden Integrale überein. In typischen Analysis-Einführungen, vor allem in der Schule, wird heute weitgehend die Darbouxsche Formulierung zur Definition benutzt. Riemannsche Summen treten oft als weiteres Hilfsmittel hinzu, etwa zum Beweis des Hauptsatzes der Integral- und Differenzialrechnung.
Ober- und Untersummen
Dieser Zugang wird meist Jean Gaston Darboux zugeschrieben.
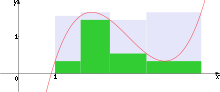
Das Integrationsintervall wird hierbei in kleinere Stücke zerlegt, der
gesuchte Flächeninhalt zerfällt dabei in senkrechte Streifen. Für jeden dieser
Streifen wird nun einerseits das größte Rechteck betrachtet, das von der
-Achse
ausgehend den Graphen nicht schneidet (im Bild grün), und andererseits das
kleinste Rechteck, das von der
-Achse
ausgehend den Graphen ganz umfasst (im Bild jeweils das grüne Rechteck zusammen
mit der grauen Ergänzung darüber). Die Summe der Flächeninhalte der großen
Rechtecke wird als Obersumme, die der kleinen als Untersumme
bezeichnet. Kann man durch geeignete, ausreichend feine Unterteilung des
Integrationsintervalles den Unterschied zwischen Ober- und Untersumme beliebig
klein machen, so gibt es nur eine Zahl, die kleiner oder gleich jeder Obersumme
und größer oder gleich jeder Untersumme ist, und diese Zahl ist der gesuchte
Flächeninhalt, das Riemannsche Integral.
Für die mathematische Präzisierung seien im Folgenden
ein Intervall
und
eine beschränkte
Funktion.
Unter einer Zerlegung
von
in
Teile versteht man eine endliche Folge
mit
.
Dann werden die zu dieser Zerlegung gehörende Ober- und Untersumme definiert
als
.
Die Funktion wird dabei durch die Treppenfunktion ersetzt, die auf jedem Teilintervall konstant gleich dem Supremum beziehungsweise Infimum der Funktion auf diesem Intervall ist.
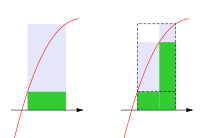
Bei einer Verfeinerung der Zerlegung wird die Obersumme kleiner, die
Untersumme größer (oder sie bleiben gleich). Einer „unendlich feinen“ Zerlegung
entsprechen also Infimum der Obersummen sowie Supremum der Untersummen; diese
werden als oberes beziehungsweise unteres darbouxsches Integral von
bezeichnet:
.
Es werden also jeweils alle möglichen Zerlegungen
des Intervalls in eine beliebige endliche Anzahl von Teilintervallen
betrachtet.
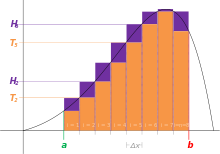
Es gilt stets
Gilt Gleichheit, so heißt
Riemann-integrierbar (oder Darboux-integrierbar), und der
gemeinsame Wert
heißt das Riemannsche Integral (oder Darboux-Integral) von
über dem Intervall
.
Riemann-Summen
Der obige Zugang zum Riemann-Integral über Ober- und Untersummen stammt, wie
dort beschrieben, nicht von Riemann selbst, sondern von Jean Gaston
Darboux. Riemann untersuchte zu einer Zerlegung
des Intervalls
und zu
gehörigen Zwischenstellen
Summen der Form
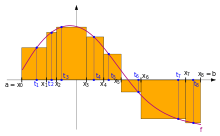
auch als Riemann-Summen oder Riemannsche Zwischensummen bezüglich der
Zerlegung
und den Zwischenstellen
bezeichnet. Riemann nannte eine Funktion
über dem Intervall
integrierbar, wenn sich die Riemann-Summen bezüglich beliebiger Zerlegungen
unabhängig von den gewählten Zwischenstellen einer festen Zahl
beliebig nähern, sofern man die Zerlegungen
nur hinreichend fein wählt. Die Feinheit einer Zerlegung Z wird dabei
über die Länge des größten Teilintervalls
,
das durch Z gegeben ist, gemessen, also durch die Zahl:
Die Zahl
ist dann das Riemann-Integral von
über
.
Ersetzt man die Veranschaulichungen „hinreichend fein“ und „beliebig nähern“
durch eine präzise Formulierung, so lässt sich diese Idee wie folgt
formalisieren.
Eine Funktion
heißt über dem Intervall
Riemann-integrierbar, wenn es zu einer festen Zahl
und zu jedem
ein
gibt, so dass für jede Zerlegung
mit
und für beliebige zu
gehörige Zwischenstellen
gilt. Die Zahl
heißt dann das Riemann-Integral von
über
und man schreibt dafür
oder
.
Riemann-Integrierbarkeit
Lebesgue-Kriterium
Eine Funktion
ist nach dem Lebesgue'schen Kriterium für Riemann-Integrierbarkeit genau
dann auf dem kompakten Intervall
Riemann-integrierbar, falls sie auf dem Intervall beschränkt und fast
überall stetig
ist. Falls die Funktion Riemann-integrierbar ist, so ist sie auch Lebesgue-integrierbar
und beide Integrale sind identisch.
Insbesondere ist über einem kompakten Intervall jede Regelfunktion, jede monoton wachsende oder monoton abnehmende Funktion und jede stetige Funktion Riemann-integrierbar.
Beispiele
Die Funktion
mit
ist stetig in allen irrationalen Zahlen und unstetig in allen rationalen Zahlen. Die Menge der Unstetigkeitsstellen liegt zwar dicht im Definitionsbereich, da diese Menge aber abzählbar ist, ist sie eine Nullmenge. Die Funktion ist damit Riemann-integrierbar.
Die Dirichlet-Funktion
mit
ist nirgendwo stetig, sie ist also nicht Riemann-integrierbar. Sie ist aber Lebesgue-integrierbar, da sie fast überall Null ist.
Die Funktion
mit
hat abzählbar viele Unstetigkeitsstellen, ist also Riemann-integrierbar. Bei Null existieren die rechts- und linksseitigen Grenzwerte nicht. Die Funktion hat dort daher eine Unstetigkeitsstelle der zweiten Art. Die Funktion ist somit keine Regelfunktion, das heißt, sie lässt sich nicht gleichmäßig durch Treppenfunktionen approximieren. Das Riemann-Integral erweitert also das Integral, das über den Grenzwert von Treppenfunktionen von Regelfunktionen definiert ist.
Uneigentliche Riemann-Integrale
Als uneigentliche Riemann-Integrale bezeichnet man:
- Integrale mit den Intervallgrenzen
oder
; dabei ist
-
,
und
mit beliebigem
- Integrale mit unbeschränkten Funktionen in einer der Intervallgrenzen; dabei ist
-
bzw.
Mehrdimensionales Riemannsches Integral
Das mehrdimensionale Riemann-Integral basiert auf dem Jordan-Maß. Sei
das n-dimensionale Jordan-Maß und sei
eine jordan-messbare Teilmenge. Außerdem sei
eine endliche Folge von Teilmengen von
mit
und
für
und sei weiter
die Funktion, welche die maximale Distanz in einer Menge
zurückgibt. Setze nun
.
Sei
eine Funktion, dann heißt die Summe
Riemannsche Zerlegung der Funktion .
Existiert der Grenzwert
,
so ist die Funktion
riemann-integrierbar und man setzt
.
Dieser Integralbegriff hat die gewöhnlichen Eigenschaften eines Integrals, die Integralfunktion ist linear und es gilt der Satz von Fubini.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.02. 2021