Lebesgue-Integral

Abbildung 1: Illustration der Grenzwertbildung beim Riemann-Integral (blau) und beim Lebesgue-Integral (rot)

Das Lebesgue-Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Integration von Funktionen ermöglicht, die auf beliebigen Maßräumen definiert sind. Im Fall der reellen Zahlen mit dem Lebesgue-Maß stellt das Lebesgue-Integral eine echte Verallgemeinerung des Riemann-Integrals dar.

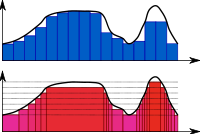
Anschaulich gesprochen bedeutet dies: Zur Annäherung des Riemann-Integrals (Abb. 1 blau) wird die Abszissenachse in Intervalle unterteilt (Partitionen) und Rechtecke gemäß dem Funktionswert an einer Stützstelle innerhalb der betreffenden Intervalle konstruiert und diese Flächen addiert. Dagegen wird zur Annäherung des Lebesgue-Integrals (Abb. 1 rot) die Ordinatenachse in Intervalle unterteilt und die Flächen zur Approximation ergeben sich aus einer Stützstelle des jeweiligen Ordinatenintervalls multipliziert mit der Gesamtlänge der Vereinigung der Urbilder des Ordinatenintervalls (gleiche Rottöne). Die Summe der so gebildeten Flächen ergibt eine Approximation des Lebesgue-Integrals. Die Gesamtlänge der Urbild-Menge wird auch als ihr Maß bezeichnet. Man vergleiche dazu auch das Zitat von Henri Lebesgue im untersten Abschnitt dieses Artikels.

So wie ein Riemann-Integral durch die Konvergenz des Flächeninhaltes einer Folge von Treppenfunktionen definiert ist, so ist das Lebesgue-Integral durch die Konvergenz einer Folge von sog. einfachen Funktionen definiert.

Geschichtliches zum Lebesgue-Integral

Die Begründung der Differential- und Integralrechnung beginnt bereits im 17. Jahrhundert mit Isaac Newton und Gottfried Wilhelm Leibniz (1687 erscheint Newtons „Philosophiae Naturalis Principia Mathematica“). Sie stellt einen Meilenstein in der Wissenschaftsgeschichte dar, besaß man doch nun zum ersten Mal ein mathematisches Konzept zur Beschreibung kontinuierlicher, dynamischer Prozesse in der Natur und – dadurch motiviert – zur Berechnung krummlinig berandeter Flächen. Es sollten aber noch viele Jahrzehnte vergehen, bis die Integralrechnung gegen Mitte des 19. Jahrhunderts durch Augustin Louis Cauchy und Bernhard Riemann auf ein solides theoretisches Fundament gestellt wurde.

Die Verallgemeinerung des so genannten Riemann-Integrals auf höherdimensionale Räume, zum Beispiel zur Berechnung der Volumina beliebiger Körper im Raum, erwies sich jedoch als schwierig. Die Entwicklung eines moderneren und leistungsfähigeren Integralbegriffes ist untrennbar mit der Entwicklung der Maßtheorie verknüpft. Tatsächlich begannen die Mathematiker erst reichlich spät systematisch zu untersuchen, wie sich beliebigen Teilmengen des $\mathbb {R} ^{n}$ in sinnvoller Weise ein Volumen zuordnen lässt. Unverzichtbare Voraussetzung für diese Arbeiten war die strenge axiomatische Begründung der reellen Zahlen durch Richard Dedekind und Georg Cantor und die Begründung der Mengenlehre durch Cantor, Ende des 19. Jahrhunderts.

Erste Antworten auf die Frage nach dem Volumen beliebiger Teilmengen des $\mathbb {R} ^{n}$ gaben zum Beispiel Giuseppe Peano und Marie Ennemond Camille Jordan. Eine befriedigende Lösung dieses Problems gelang aber erst Émile Borel und Henri Lebesgue durch die Konstruktion des Lebesgue-Maßes. 1902 formulierte Lebesgue in seiner Pariser Thèse zum ersten Mal das moderne Maßproblem und wies explizit darauf hin, es nicht in voller Allgemeinheit lösen zu können, sondern nur für eine ganz bestimmte Klasse von Mengen, die er messbare Mengen nannte. Tatsächlich sollte sich herausstellen, dass das Maßproblem nicht allgemein lösbar ist, d. h. tatsächlich Mengen existieren, denen man kein sinnvolles Maß zuordnen kann (sieheSatz von Vitali, Banach-Tarski-Paradoxon). Durch die Konstruktion des Lebesgue-Maßes stand nun der Weg für einen neuen, verallgemeinerbaren Integralbegriff offen. Die erste Definition des Lebesgue-Integrals gab denn auch Henri Lebesgue in seiner Thèse gleich selbst. Weitere bedeutende Definitionen des Lebesgue-Integrals stammten wenig später von William Henry Young (1905) und Frigyes Riesz (1910). Die nachfolgend vorgestellte Definition, die mittlerweile in der Fachliteratur am üblichsten ist, folgt der Konstruktion Youngs.

Heutzutage ist das Lebesgue-Integral der Integralbegriff der modernen Mathematik. Seine Verallgemeinerbarkeit und seine – aus mathematischer Sicht – schönen Eigenschaften machen ihn auch zu einem unverzichtbaren Werkzeug in der Funktionalanalysis, der Physik und der Wahrscheinlichkeitstheorie.

Zur Konstruktion des Lebesgue-Integrals

Maßraum und messbare Mengen

Das Lebesgue-Integral wird für Funktionen auf einem beliebigen Maßraum definiert. Vereinfacht gesagt ist ein Maßraum eine Menge $\Omega$ mit einer zusätzlichen Struktur, die es erlaubt, bestimmten Teilmengen ein Maß zuzuordnen, z.B. ihre geometrische Länge (bzw. ihr Volumen). Das Maß, das dieses leistet, heißt Lebesgue-Maß. Eine Teilmenge von $\Omega$ , der man ein Maß zuordnen kann, heißt messbar. Ist eine messbare Menge, so bezeichnet man mit ${\mathcal {\mu }}(A)$ das Maß von . Das Maß einer messbaren Menge ist eine nichtnegative reelle Zahl oder $+\infty$ . Für das Lebesgue-Maß einer Teilmenge des $\mathbb {R} ^{n}$ schreibt man stattdessen üblicherweise ${\mathcal {\lambda }}(A)$ .

Integration einfacher Funktionen

So wie das Riemann-Integral mittels Approximation durch Treppenfunktionen konstruiert wird, konstruiert man das Lebesgue-Integral mit Hilfe sogenannter einfacher Funktionen. Diese Vorgehensweise wird manchmal auch als „algebraische Induktion“ bezeichnet und findet in vielen Beweisen für messbare Funktionen Verwendung. Eine einfache Funktion, auch Elementarfunktion genannt, ist eine nicht-negative messbare Funktion, die nur endlich viele Funktionswerte $\alpha _{i}$ annimmt. Somit lässt sich jede einfache Funktion $\phi$ schreiben als

$\phi =\sum _{i=1}^{n}\alpha _{i}\chi _{A_{i}}$ .

Dabei ist $\alpha _{i}$ eine positive reelle Zahl, $A_{i}$ die (messbare) Menge, auf der die Funktion den Wert $\alpha _{i}$ annimmt, und $\chi _{A_{i}}$ die charakteristische Funktion zu $A_{i}$ .

Nun lässt sich auf sehr natürliche Weise das Integral einer einfachen Funktion definieren:

$\int _{\Omega }\phi \ \mathrm {d} \mu =\sum _{i=1}^{n}\alpha _{i}\mu (A_{i})$

Das Integral von $\phi$ über $\Omega$ ist also einfach die Summe der Produkte aus Funktionswert von $\phi$ und Maß der Menge, auf der die Funktion den jeweiligen Wert annimmt.

Integration nicht-negativer Funktionen

Nun definiert man zunächst das Integral für nicht-negative Funktionen, d.h. für Funktionen, die keine negativen Werte annehmen. Voraussetzung für die Integrierbarkeit einer Funktion ist ihre Messbarkeit.

Eine nicht-negative Funktion $f\colon \left(\Omega ,\Sigma ,\mu \right)\rightarrow ({\overline {\mathbb {R} }},B)$ , Borelsche σ-Algebra, ist genau dann messbar, wenn es eine Folge $(f_{n})_{n\in \mathbb {N} }$ von einfachen Funktionen gibt, die punktweise und monoton wachsend gegen konvergiert. Man definiert nun das Integral einer nicht-negativen, messbaren Funktion durch

$\int _{\Omega }f\mathrm {d} \mu =\lim _{n\rightarrow \infty }\int _{\Omega }f_{n}\mathrm {d} \mu$ ,

wobei die $f_{n}$ einfach sind und punktweise und monoton wachsend gegen konvergieren. Der Limes ist von der speziellen Wahl der Folge $f_{n}$ unabhängig. Das Integral kann auch den Wert $+\infty$ annehmen.

Häufig findet man in der Literatur auch folgende äquivalente Definition:

$\int _{\Omega }f\mathrm {d} \mu =\sup \left\lbrace \int _{\Omega }\phi \,\mathrm {d} \mu \,\vert \,\phi \ {\text{einfach}},0\leq \phi \leq f\right\rbrace$

Man definiert also das Integral einer nicht-negativen messbaren Funktion, indem man die Funktion „von unten“ beliebig genau durch einfache Funktionen approximiert.

Integration beliebiger messbarer Funktionen und Integrierbarkeit

Um das Integral einer beliebigen messbaren Funktion zu definieren, zerlegt man diese in ihren positiven und negativen Anteil, integriert diese beiden einzeln und zieht die Integrale voneinander ab. Das ergibt aber nur dann einen Sinn, wenn die Werte dieser beiden Integrale endlich sind (zumindest der Wert eines der beiden Integrale).

Der Positivteil $f^{+}$ einer Funktion ist (punktweise) definiert als $f^{+}=\max\{f,0\}$ .

Der Negativteil $f^{-}$ wird entsprechend (punktweise) durch $f^{-}=\max\{-f,0\}$ definiert.

Es gilt dann (punktweise) $f^{+}\geq 0$ , $f^{-}\geq 0$ , $f=f^{+}-f^{-}$ und $f^{+}+f^{-}=|f|$ .

Eine Funktion heißt µ-quasiintegrierbar oder quasiintegrierbar bezüglich des Maßes µ, wenn mindestens eines der beiden Integrale

$\int _{\Omega }f^{+}\ \mathrm {d} \mu$ und $\displaystyle \int _{\Omega }f^{-}\ \mathrm {d} \mu$

endlich ist.

In diesem Falle heißt

$\int _{\Omega }f\ \mathrm {d} \mu =\int _{\Omega }f^{+}\ \mathrm {d} \mu -\int _{\Omega }f^{-}\mathrm {d} \mu$ .

das $\mu$ -Integral von über $\Omega$ .

Für alle messbaren Teilmengen $A\subseteq \Omega$ ist dann

$\int _{A}f\mathrm {d} \mu =\int _{\Omega }f\cdot \chi _{A}\ \mathrm {d} \mu$

das $\mu$ -Integral von über .

Eine Funktion heißt µ-integrierbar oder integrierbar bezüglich des Maßes µ, wenn beide Integrale

$\int _{\Omega }f^{+}\ \mathrm {d} \mu$ und $\displaystyle \int _{\Omega }f^{-}\ \mathrm {d} \mu$

endlich sind. Äquivalent dazu ist die Bedingung

$\int _{\Omega }|f|\,\mathrm {d} \mu <\infty$ .

Offensichtlich ist jede integrierbare Funktion quasiintegrierbar.

Schreibweisen

Für das Lebesgue-Integral werden zahlreiche Schreibweisen verwendet: Im Folgenden sei $A\subseteq \Omega$ eine messbare Menge. Will man bei der Integration die Integrationsvariable angeben, so schreibt man

$\int _{A}f(x)\,\mathrm {d} \mu (x)$ oder $\int _{A}f(x)\,\mu (\mathrm {d} x)$ oder auch $\int _{A}\mu (\mathrm {d} x)\,f(x)$ .

Ist $\mu$ das Lebesgue-Maß, so schreibt man statt $\mathrm {d} \mu (x)$ einfach $\mathrm {d} x$ , im eindimensionalen Fall $\Omega =\mathbb {R}$ schreibt man auch

$\int _{a}^{b}f(x)\,\mathrm {d} x$

für das Integral über das Intervall [a,b] oder ]a,b[ .

Wenn das Maß $\mu$ eine Radon-Nikodým-Dichte bezüglich des Lebesgue-Maßes besitzt, gilt

$\int _{A}f(x)\,\mathrm {d} \mu (x)=\int _{A}f(x)\,h(x)\mathrm {d} x$ .

In Anwendungsgebieten wird die Schreibweise

$\int _{A}f(x)\,h(x)\,\mathrm {d} x$

häufig auch dann verwendet, wenn $\mu$ formal keine Dichte besitzt. Dies ist jedoch nur dann sinnvoll, wenn man nicht als Funktion, sondern als Distribution auffasst.

Ist das Maß $\mu$ im Fall $\Omega =\mathbb {R}$ durch eine Verteilungsfunktion definiert, so schreibt man auch

$\int _{A}f(x)\,\mathrm {d} F(x)$ oder $\int _{A}f\,\mathrm {d} F$

(Lebesgue-Stieltjes-Integral).

Ist $\mu$ ein Wahrscheinlichkeitsmaß, so schreibt man auch $\mathbb {E} (f)$ für

$\int _{\Omega }f\,\mathrm {d} \mu \,$

(Erwartungswert). In der theoretischen Physik wird die Schreibweise $\langle f\rangle$ verwendet, in der Funktionalanalysis manchmal die Schreibweise $\ \mu (f)\$ .

Nullmengen und fast überall bestehende Eigenschaften

Eine Menge $N\subset \Omega$ , die das Maß 0 besitzt, heißt Nullmenge, im Falle des Lebesgue-Maßes auch speziell Lebesgue-Nullmenge. Ist also $N\subset \Omega$ mit $\ \mu (N)=0\$ und eine integrierbare Funktion, so gilt:

$\int _{\Omega }f\,\mathrm {d} \mu =\int _{\Omega \setminus N}f\,\mathrm {d} \mu +\int _{N}f\,\mathrm {d} \mu =\int _{\Omega \setminus N}f\,\mathrm {d} \mu$

da das Integral über die Nullmenge den Wert 0 annimmt. ( $\Omega \setminus N$ bezeichnet die Menge $\Omega$ ohne die Menge )

Folglich ändert sich der Wert des Integrals nicht, wenn man die Funktion auf einer Nullmenge ändert. Besitzt eine Funktion eine Eigenschaft (Stetigkeit, punktweise Konvergenz etc.) auf dem gesamten Definitionsbereich mit Ausnahme einer Menge vom Maß 0, so sagt man, diese Eigenschaft bestehe fast überall. In der Lebesgue’schen Integrationstheorie ist es folglich oft sinnvoll, zwei Funktionen, die fast überall übereinstimmen, auch als gleich anzusehen – man fasst sie zu einer Äquivalenzklasse zusammen (siehe hierzu auch L^p).

Es ist sogar oft so, dass man Funktionen, die nur fast überall definiert sind (z.B. der punktweise Limes einer Funktionenfolge, die nur fast überall konvergiert), als Funktionen auf dem ganzen Raum auffasst und ohne Bedenken

$\int _{\Omega }f\,d\mu$

schreibt, auch wenn gar nicht auf ganz $\Omega$ definiert ist. Dieses Vorgehen ist dadurch gerechtfertigt, dass jede Fortsetzung von sich nur auf einer Nullmenge von unterscheidet und somit das Integral der Fortsetzung über ganz $\Omega$ den gleichen Wert hat wie das Integral über $\Omega \setminus N$ .

Man muss beachten, dass eine Nullmenge nur im Sinne des Maßes vernachlässigbar „klein“ ist. Sie kann aber auch durchaus unendlich viele Elemente enthalten. So ist zum Beispiel die Menge $\mathbb {Q} \subset \mathbb {R}$ , also die Menge der rationalen Zahlen als Teilmenge der reellen Zahlen eine Lebesgue-Nullmenge. Die Dirichlet-Funktion

$f(x)={\begin{cases}1&x\in \mathbb {Q} \\0&{\text{sonst}}\end{cases}}$

ist also im oben genannten Sinne gleich der Funktion, die konstant den Wert Null annimmt (Nullfunktion), obwohl es keine noch so kleine Umgebung gibt, in der ihre Werte übereinstimmen. Eine bekannte überabzählbare (zu $\mathbb {R}$ gleichmächtige) Lebesgue-Nullmenge ist die Cantor-Menge.

Wichtige Eigenschaften des Lebesgue-Integrals

Das Integral ist linear in ${\mathcal {L}}^{1}$ (Raum der integrierbaren Funktionen), d. h. für integrierbare Funktionen $\ f\$ und $\ g\$ und beliebige $\alpha ,\beta \in \mathbb {R}$ ist auch $\ \alpha f+\beta g\$ integrierbar und es gilt:

$\int _{\Omega }(\alpha f+\beta g)\,\mathrm {d} \mu =\alpha \cdot \int _{\Omega }f\,\mathrm {d} \mu +\beta \cdot \int _{\Omega }g\,\mathrm {d} \mu$

Das Integral ist monoton, d. h. sind $\ f\$ und $\ g\$ zwei messbare Funktionen mit $f\leq g$ , so gilt

$\int _{\Omega }f\ \mathrm {d} \mu \leq \int _{\Omega }g\ \mathrm {d} \mu$ .

Das Integral kann getrennt werden

$\int _{\Omega }f\ \mathrm {d} \mu =\int _{\Omega \backslash N}f\ \mathrm {d} \mu +\int _{N}f\ \mathrm {d} \mu$

$\int _{\Omega \cup N}f\ \mathrm {d} \mu =\int _{\Omega }f\ \mathrm {d} \mu +\int _{N}f\ \mathrm {d} \mu -\int _{\Omega \cap N}f\ \mathrm {d} \mu$

Ist $A\in {\mathcal {P}}(\Omega )$ messbar mit $\ \mu (A)=0\$ , so gilt

$\ \int _{A}f\mathrm {d} \mu =0\$

Konvergenzsätze

Einer der wichtigsten Vorzüge des Lebesgue-Integrals sind die aus mathematischer Sicht sehr schönen Konvergenzsätze. Dies betrifft die Vertauschbarkeit von Grenzwert und Integral bei Funktionenfolgen der Form $\ (f_{n})_{n\in \mathbb {N} }\$ . Die wichtigsten Konvergenzsätze sind:

Satz von der monotonen Konvergenz (Beppo Levi, 1906)

Ist $f_{n}\colon (\Omega ,\Sigma ,\mu )\rightarrow ({\overline {\mathbb {R} }},B),n\in \mathbb {N}$ eine monoton wachsende Folge von nichtnegativen, messbaren Funktionen, so gilt:

$\int _{\Omega }\sup _{n\in \mathbb {N} }f_{n}\ \mathrm {d} \mu =\int _{\Omega }\lim _{n\rightarrow \infty }f_{n}\ \mathrm {d} \mu =\lim _{n\rightarrow \infty }\int _{\Omega }f_{n}\ \mathrm {d} \mu$ .

Satz von der majorisierten (dominierten) Konvergenz (Henri Léon Lebesgue, 1910): Konvergiert die Folge der messbaren Funktionen $f_{n}\colon (\Omega ,\Sigma ,\mu )\rightarrow ({\overline {\mathbb {R} }},B)$ $\mu$ -fast überall gegen die messbare Funktion $f\colon (\Omega ,\Sigma ,\mu )\rightarrow ({\overline {\mathbb {R} }},B)$ und sind die Funktionen $f_{n}$ , $n\in \mathbb {N}$ , betragsmäßig $\mu$ -fast überall durch eine integrierbare Funktion $g\colon (\Omega ,\Sigma ,\mu )\rightarrow ({\overline {\mathbb {R} }},B)$ beschränkt, dann gilt:

ist integrierbar,
$\lim _{n\rightarrow \infty }\int _{\Omega }f_{n}\ \mathrm {d} \mu =\int _{\Omega }f\ \mathrm {d} \mu$ und
$\lim _{n\rightarrow \infty }\int _{\Omega }|f-f_{n}|\ \mathrm {d} \mu =0.$

Lemma von Fatou (Pierre Fatou, 1906)

Sind $f_{n}\colon (\Omega ,\Sigma ,\mu )\rightarrow ({\overline {\mathbb {R} }},B)$ , $n\in \mathbb {N}$ , nichtnegative messbare Funktionen, dann gilt:

$\int _{\Omega }\liminf _{n\rightarrow \infty }f_{n}\ \mathrm {d} \mu \leq \liminf _{n\rightarrow \infty }\int _{\Omega }f_{n}\ \mathrm {d} \mu$

Riemann- und Lebesgue-Integral

Im Fall $\Omega =\mathbb {R}$ mit dem Lebesgue-Maß gilt: Ist eine Funktion auf einem kompakten Intervall Riemann-integrierbar, so ist sie auch Lebesgue-integrierbar und die Werte beider Integrale stimmen überein. Hingegen ist nicht jede Lebesgue-integrierbare Funktion auch Riemann-integrierbar.

Allerdings muss eine uneigentlich Riemann-integrierbare Funktion nicht als Ganzes Lebesgue-integrierbar sein; der entsprechende Grenzwert von Lebesgue-Integralen existiert jedoch nach den obigen Bemerkungen und liefert denselben Wert wie für die Riemann-Integrale. Ist aber |f| uneigentlich Riemann-integrierbar, dann ist sogar als Ganzes Lebesgue-integrierbar.

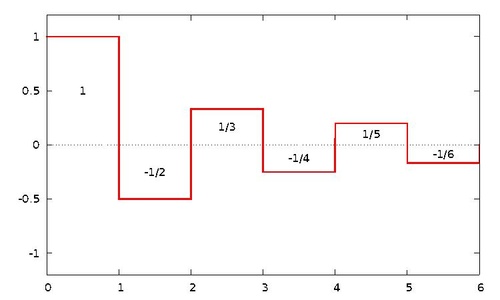
Man kann leicht ein Beispiel einer uneigentlich Riemann-integrierbaren Funktion angeben, die nicht Lebesgue-integrierbar ist: Ist nämlich f eine Treppenfunktion mit den Flächen 1, -1/2, 1/3 usw., dann ist f uneigentlich Riemann-integrierbar. Denn das Integral entspricht gerade der alternierenden harmonischen Reihe. Wäre f Lebesgue-integrierbar, so würde $\textstyle \int _{\mathbb {R} ^{+}}|f|\,\mathrm {d} \lambda <\infty$ gelten. Dies ist jedoch nicht der Fall, da die harmonische Reihe divergent ist. Folglich existiert das entsprechende Lebesgue-Integral nicht. Die Situation ist in Abbildung 2 wiedergegeben.

Abbildung 2

Wichtiger ist der umgekehrte Fall einer Lebesgue-integrierbaren Funktion, die nicht Riemann-integrierbar ist.

Das bekannteste Beispiel dafür ist die Dirichlet-Funktion:

$f\colon [0,1]\rightarrow [0,1]$

$x\mapsto {\begin{cases}1&,x\in \mathbb {Q} \\0&,{\text{sonst}}.\end{cases}}$

f ist nicht Riemann-integrierbar, da alle Untersummen stets 0 und alle Obersummen stets 1 sind. Da aber $\mathbb {Q} \,,$ die Menge der rationalen Zahlen, in der Menge der reellen Zahlen eine Lebesgue-Nullmenge ist, ist die Funktion fast überall 0. Also existiert das Lebesgue-Integral und besitzt den Wert 0.

Der wesentliche Unterschied im Vorgehen bei der Integration nach Riemann bzw. Lebesgue besteht darin, dass beim Riemann-Integral der Definitionsbereich (Abszisse), beim Lebesgue-Integral jedoch die Bildmenge (Ordinate) der Funktion unterteilt wird. An obigen Beispielen lässt sich bereits erkennen, dass sich dieser Unterschied durchaus als entscheidend herausstellen kann.

Henri Lebesgue über den Vergleich zwischen Riemann- und Lebesgue-Integral

„Man kann sagen, dass man sich bei dem Vorgehen von Riemann verhält wie ein Kaufmann ohne System, der Geldstücke und Banknoten zählt in der Reihenfolge, wie er sie in die Hand bekommt; während wir vorgehen wie ein umsichtiger Kaufmann, der sagt:

Ich habe $m(E_{1})$ Münzen zu einer Krone, macht $1\cdot m(E_{1})$ ,

ich habe $m(E_{2})$ Münzen zu zwei Kronen, macht $2\cdot m(E_{2})$ ,

ich habe $m(E_{3})$ Münzen zu fünf Kronen, macht $5\cdot m(E_{3})$ ,

usw., ich habe also insgesamt $S=1\cdot m(E_{1})+2\cdot m(E_{2})+5\cdot m(E_{3})+\ldots$ .
Die beiden Verfahren führen sicher den Kaufmann zum gleichen Resultat, weil er – wie reich er auch sei – nur eine endliche Zahl von Banknoten zu zählen hat; aber für uns, die wir unendlich viele Indivisiblen zu addieren haben, ist der Unterschied zwischen beiden Vorgehensweisen wesentlich.“

– Henri Lebesgue, 1926: nach Jürgen Elstrodt

Bochner-Integral

→ Hauptartikel: Bochner-Integral

Eine direkte Verallgemeinerung des Lebesgue-Integrals für Banachraum-wertige Funktionen stellt das Bochner-Integral dar. Es erbt fast alle Eigenschaften des Lebesgue-Integrals, wie zum Beispiel den Satz von der majorisierten Konvergenz.

Basierend auf einem Artikel in:

Wikipedia.de