
Stieltjesintegral
In der Integralrechnung bezeichnet das Stieltjesintegral eine wesentliche Verallgemeinerung des Riemannintegrals oder eine Konkretisierung des Integralbegriffs von Lebesgue. Benannt wurde es nach dem niederländischen Mathematiker Thomas Jean Stieltjes (1856–1894). Das Stieltjesintegral, für den der Begriff des Integrators grundlegend ist, findet in vielen Gebieten Anwendung, insbesondere in der Physik und der Stochastik.
Das Riemann-Stieltjes-Integral für monotone Integratoren
Es seien
mit
und
zwei Funktionen.
Dabei wird vorausgesetzt, dass
,
der Integrand, beschränkt ist und
,
der Integrator, (nicht notwendigerweise streng) monoton
wächst. Das dazugehörige Riemann-Stieltjes-Integral von
bezüglich
auf dem Intervall
wird wie das Riemannintegral
über feine Zerlegungen des Intervalls oder über Ober- und Untersummen (siehe
dort) definiert. Jedoch lauten die Formeln für die Ober- und Untersumme bei
Stieltjes-Integralen statt
(Obersumme) und
(Untersumme)
nun
(Stieltjes-Obersumme) und
(Stieltjes-Untersumme).
Konvergieren Ober- und Untersumme für hinreichend feine Zerlegungen gegen
denselben Wert, so heißt
bezüglich
auf
Riemann-Stieltjes-integrierbar und der gemeinsame Grenzwert wird als
Wert des Integrals bezeichnet. Die Schreibweise hierfür ist
Der Integrator
regelt also, wie stark
an verschiedenen Stellen gewichtet wird. Statt Integrator ist deshalb
auch die Bezeichnung Gewichtsfunktion üblich. Offensichtlich kann das
gewöhnliche Riemannintegral als Spezialfall des Riemann-Stieltjes-Integrals mit
für alle
(Identität)
aufgefasst werden. Im Unterschied zum Riemann-Integral setzt man zwar
standardmäßig voraus, dass die Integrandenfunktion
stetig ist, die Integratorfunktion
kann aber komplizierter sein:
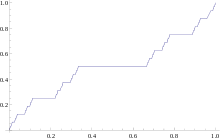

Das Riemann-Stieltjes-Integral existiert z. B. bei stetiger Funktion
selbst mit der Cantor-Funktion
als Integrator
(das ist eine monoton von 0 auf 1 wachsende stetige Funktion, deren Ableitung
fast überall 0 ist, nämlich bis auf eine überabzählbare Nullmenge). Es existiert
sogar mit einer unstetigen, aber monotonen Sprungfunktion
etwa für
für alle
,
aber
für
(Heaviside-Funktion).
Das Lebesgue-Stieltjes-Integral
Das Lebesgue-Stieltjes-Integral ist ein Spezialfall des Lebesgue-Integrals.
Hierbei wird über ein Borel-Maß
integriert, das im Fall des Lebesgue-Stieltjes-Integrals durch die monotone
Funktion
definiert wird und im Folgenden mit
bezeichnet wird. Das Maß
ist festgelegt durch seine Werte auf Intervallen:
Hier bezeichnet
den linksseitigen und
den rechtsseitigen Grenzwert
der Funktion
an der Stelle
.
Ist
die Identität, so handelt es sich um das Lebesgue-Maß.
Ist
bezüglich dieses Maßes
Lebesgue-integrierbar, so definiert man das zugehörige
Lebesgue-Stieltjes-Integral als
wobei die rechte Seite als gewöhnliches Lebesgue-Integral aufzufassen ist.
Nicht-monotone Integratoren
Für eine eingeschränkte Menge nicht monoton wachsender Integratoren kann das
Stieltjes-Integral ebenfalls sinnvoll definiert werden, nämlich für solche mit
endlicher Variation
auf .
Funktionen endlicher Variation können nämlich stets als Differenz zweier monoton
wachsender Funktionen dargestellt werden, also
wobei
monoton wachsend sind. Das zugehörige Stieltjes-Integral (wahlweise im
Riemannschen oder Lebesgueschen Sinne) ist dann definiert als
Es kann gezeigt werden, dass diese Definition sinnvoll, d.h. wohldefiniert (also unabhängig von der speziellen Wahl der Zerlegung) ist.
Eigenschaften
- Wie das Riemann- und das Lebesgue-Integral ist auch das Stieltjes-Integral
linear im Integranden:
- für Konstanten
, falls die betrachteten Integrale existieren.
- Weiterhin ist das Stieltjes-Integral auch linear im Integrator, also
- für Konstanten
und Funktionen
> endlicher Variation.
- Das Integral ist invariant unter Translationen
des Integrators, also
- für Konstanten
.
- Treppenfunktionen
als Integratoren: Ist
stetig und
eine Treppenfunktion, die in den Punkten
Sprünge der Höhe
besitzt, so gilt
- Ist
stetig differenzierbar, so gilt
- (Im Lebesgueschen Sinne:
ist die Dichte von
.)
- Ist
absolut stetig, so ist
fast überall differenzierbar, die Ableitung
ist integrierbar und es gilt auch hier:
- Für das Riemann-Stieltjes-Integral gilt folgende Regel zur partiellen
Integration:
Literatur
- Isidor P. Natanson: Theorie der Funktionen einer reellen Veränderlichen. Unveränderter Nachdruck der 4. Auflage. Harri Deutsch, Thun u. a. 1981, ISBN 3-87-144-217-8.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.11. 2020