Heaviside-Funktion

Die Heaviside-Funktion, auch Theta-, Treppen-, Schwellenwert-, Stufen-, Sprung- oder Einheitssprungfunktion genannt, ist eine in der Mathematik und Physik oft verwendete Funktion. Sie ist nach dem britischen Mathematiker und Physiker Oliver Heaviside (1850–1925) benannt.

Allgemeines

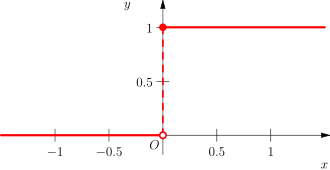
Die Heaviside-Funktion hat für jede beliebige negative Zahl den Wert null, andernfalls den Wert eins. Die Heaviside-Funktion ist mit Ausnahme der Stelle x=0 überall stetig. In Formeln geschrieben heißt das:

Heaviside-Funktion

${\begin{aligned}\Theta \colon &\mathbb {R} \to \{0,1\}\\\ &x\mapsto {\begin{cases}0:&x<0\\1:&x\geq 0\end{cases}}\end{aligned}}$

Sie ist also die charakteristische Funktion des Intervalls $[0,+\infty)$ der nichtnegativen reellen Zahlen.

In der Fachliteratur ist statt $\Theta(x)$ auch eine davon abweichende Nomenklatur geläufig:

, welche sich am Namen von Oliver Heaviside orientiert.
> und $\sigma(x)$ nach der Bezeichnung Sprungfunktion.
nach der Bezeichnung englisch unit step function.
Auch $\epsilon(x)$ wird häufig verwendet.
In der Systemtheorie verwendet man auch das Symbol .

Die Funktion findet zahlreiche Anwendungen, etwa in der Nachrichtentechnik oder als mathematisches Filter: Multipliziert man punktweise jeden Wert einer beliebigen stetigen Funktion mit dem entsprechenden Wert der Heaviside-Funktion, ergibt sich eine Funktion, die links von x=0 den Wert Null hat (deterministische Funktion), rechts davon aber mit der ursprünglichen Funktion übereinstimmt.

Alternative Darstellungen

Den Wert der Heaviside-Funktion an der Stelle x=0 kann man auch folgendermaßen festlegen. Zur Kennzeichnung der Definition schreibt man

${\begin{aligned}\Theta _{c}\colon &\mathbb {R} \to \mathbb {K} \\\,&x\mapsto {\begin{cases}0:&x<0\\c:&x=0\\1:&x>0\end{cases}}\end{aligned}}$

mit $0,1,c\in\mathbb{K}$ . Es kann $\mathbb {K}$ also eine beliebige Menge darstellen, solange sie 0 und 1 enthält. Üblicherweise wird jedoch $\mathbb{K} = [0,1] \subset \R$ verwendet.

Diese Definition ist charakterisiert durch die Eigenschaft, dass dann $\Theta_c(0) = c$ ist.

Durch die Wahl $c := \tfrac{1}{2}$ und folglich $\Theta_\frac{1}{2}(0) = \textstyle\frac{1}{2}$ erreicht man, dass die Gleichungen

$\Theta_\frac{1}{2}(x) = \tfrac{1}{2}(\sgn{(x)} + 1)$ und damit auch

$\Theta_\frac{1}{2}( -x ) = 1 - \Theta_\frac{1}{2}(x)$

für alle reellen gültig sind.

Eine Integralrepräsentation der Heaviside-Sprungfunktion lautet wie folgt:

$\Theta(x)=\lim_{ \varepsilon \to 0} -{1\over 2\pi i}\int_{-\infty}^\infty {1 \over \tau+i\varepsilon} e^{-i x \tau} \, \mathrm d \tau$

Eine weitere Repräsentation ist gegeben durch:

$\Theta(x)=\lim_{\varepsilon\to 0}{1\over\pi}\left[ \arctan \left( {x\over\varepsilon} \right)+{\pi\over 2} \right]$

Eigenschaften

Differenzierbarkeit

Die Heaviside-Funktion ist weder im klassischen Sinne differenzierbar noch ist sie schwach differenzierbar. Dennoch kann man über die Theorie der Distributionen eine Ableitung definieren. Die Ableitung der Heaviside-Funktion in diesem Sinne ist die diracsche Delta-Distribution, die in der Physik zur Beschreibung von punktförmigen Quellen von Feldern Verwendung findet.

$\frac{\mathrm d}{\mathrm dx}\Theta(x) = \delta(x)$