Antiprisma
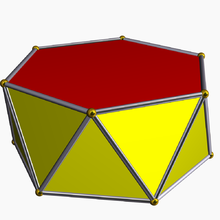
Ein Antiprisma (Mehrzahl: Antiprismen) ist ein geometrischer Körper, der ein Vieleck als Grundfläche und ein gleichartiges Vieleck als Deckfläche hat, die zueinander parallel, aber verdreht sind. Diese beiden Flächen sind durch ein umlaufendes Band von Dreiecksflächen verbunden, deren Spitzen abwechselnd zur Grund- und zur Deckfläche weisen.
Antiprismen sind spezielle Polyeder. Sie ähneln Prismen und gehören ebenso wie diese zu den Prismatoiden. Im Unterschied zu Prismen haben sie jedoch doppelt so viele Mantelflächen (bei gleicher Eckenzahl) und die Mantelflächen sind Dreiecke anstatt Parallelogramme.
Besondere Antiprismen
Bei geraden Antiprismen ist die Grund- und Deckfläche ein regelmäßiges
n-Eck und 2n gleichschenklige
Dreiecke bilden den Mantel. Die Mittelpunkte der Grund- und Deckflächen
liegen genau übereinander und die Deckfläche ist um den Winkel
gegenüber der Grundfläche gedreht. Bei geraden Antiprismen sind alle Ecken
gleichartig. Die dualen
Polyeder zu geraden Antiprismen sind Trapezoeder.
Ein uniformes Antiprisma hat zusätzlich die Bedingung, dass seine Mantelflächen gleichseitige Dreiecke sind. Ein Beispiel dafür ist das Oktaeder, das sich (auch) als ein uniformes Antiprisma mit dreieckiger Grundfläche beschreiben lässt.
Das diagonale Antiprisma, auch Disphenoid genannt, ist ein entarteter Sonderfall, bei dem die Grund- und Deckfläche zu einem Zweieck reduziert ist. Ein uniformes diagonales Antiprisma ist ein regelmäßiges Tetraeder.
Beispiele für uniforme Antiprismen:
-
 Diagonales (zweieckiges) Antiprisma: Tetraeder
Diagonales (zweieckiges) Antiprisma: Tetraeder -
 Trigonales (dreieckiges) Antiprisma: Oktaeder
Trigonales (dreieckiges) Antiprisma: Oktaeder -
 Tetragonales (quadratisches) Antiprisma
Tetragonales (quadratisches) Antiprisma -
 Pentagonales (fünfeckiges) Antiprisma
Pentagonales (fünfeckiges) Antiprisma
s.a. Ikosaeder -
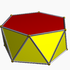 Hexagonales (sechseckiges) Antiprisma
Hexagonales (sechseckiges) Antiprisma -
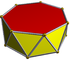 Heptagonales (siebeneckiges) Antiprisma
Heptagonales (siebeneckiges) Antiprisma -
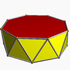 Oktogonales (achteckiges) Antiprisma
Oktogonales (achteckiges) Antiprisma -
 Nonagonales (neuneckiges) Antiprisma
Nonagonales (neuneckiges) Antiprisma -
 Dekagonales (zehneckiges) Antiprisma
Dekagonales (zehneckiges) Antiprisma -
 Hendekagonales (elfeckiges) Antiprisma
Hendekagonales (elfeckiges) Antiprisma -
 Dodekagonales (zwölfeckiges) Antiprisma
Dodekagonales (zwölfeckiges) Antiprisma
Symmetrie
Besitzt ein Antiprisma ein regelmäßiges -Eck
als Grundseite und ist die Deckfläche um den Winkel
gegenüber der Grundfläche gedreht, dann und nur dann ist das Antiprisma punktsymmetrisch wenn
ungerade ist.
Beispiele:
- Das Oktaeder mit einer ungeraden Anzahl von Eckpunkten der Grundseite (Dreieck) ist punktsymmetrisch.
- Das Tetraeder mit einer geraden Anzahl von Eckpunkten der Grundseite (Zweieck) ist nicht punktsymmetrisch.
Kartesische Koordinaten
Kartesische Koordinaten für die Ecken eines geraden Antiprismas mit n-eckiger Grundfläche und gleichschenkligen Dreiecken sind
wobei k Werte von 0 bis 2n−1 annimmt; wenn die Dreiecke gleichseitig sind, ist
Volumen und Oberfläche
Die Kantenlänge eines uniformen n-eckigen Antiprismas sei mit a gegeben. Dann ist sein Volumen
und seine Oberfläche
Umkugel
Der Radius
der Umkugel bei gegebener Höhe
und gegebenem Umkreisradius
der Grundfläche berechnet sich nach dem Satz
des Pythagoras zu:
(Wegen seiner vier Ecken besitzt auch jedes unregelmäßige Tetraeder eine Umkugel. Dieses pathologische Prisma wird hier aber ignoriert.)
Kantenkugel
Nur uniforme Antiprismen haben eine Kantenkugel.
Der Radius
der Kantenkugel bei gegebener Höhe
und gegebenem Inkreisradius
berechnet sich nach dem Satz des Pythagoras zu:
Inkugel
Wegen seiner vier Flächen besitzt jeder Vierflächner eine Inkugel.
Ansonsten besitzen nur gerade Antiprismen, deren Höhe das Doppelte des
Inkugelradius beträgt, eine Inkugel. Für diese Körper ergibt sich der Radius
der Inkugel bei gegebenem Umkreisradius
und gegebenem Inkreisradius
der Grund- beziehungsweise Deckfläche zu:
Ein Antiprisma mit einer Inkugel besteht i.a. aus gleichschenkligen Dreiecken als Mantelflächen. Lediglich das Oktaeder (neben dem regelmäßigen Tetraeder) ist das einzige Antiprisma mit gleichseitigen Dreiecken als Mantelflächen.
Netz
Für das Netz von Antiprismen gibt es verschiedene Möglichkeiten. Eine ist, zunächst ein Band von Dreiecken für den Mantel zu definieren und an dieses Band dann die Grund- und Deckfläche anzufügen. Zwei andere Möglichkeiten zeigen die folgenden Grafiken.
-
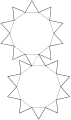 Netz eines geraden/uniformen Antiprismas
Netz eines geraden/uniformen Antiprismas -
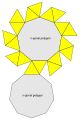 Eine andere Art, das Netz zu bilden
Eine andere Art, das Netz zu bilden -
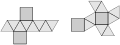 Zwei Netzdarstellungen eines quadratischen Antiprismas
Zwei Netzdarstellungen eines quadratischen Antiprismas
Vorkommen
Antiprismen finden sich unter anderem als Koordinationspolyeder in Kristallstrukturen und Komplexverbindungen, als Kapside von Viren, und in Walzenwürfeln.
Gerüste aus Stäben oder Rohren, die die Kanten von Antiprismen bilden, sind um die Hauptachse um vieles torsionssteifer und knickfester als entsprechende Prismen, weshalb sie gerne als Podeste im Zirkus verwendet werden.
In der Architektur wird das Antiprisma gelegentlich eingesetzt. Das One World Trade Center in New York City hat hauptsächlich die Form eines langgezogenen quadratischen Antiprismas, wobei allerdings das obere Quadrat kleiner als das untere ist. Der Diagonal Tower in Seoul besteht aus drei aufeinandergestellten quadratischen Antiprismen. Sein Design soll die entstehenden Windkräfte reduzieren und zugleich Materialersparnis einbringen.
-

8-seitiger Antiprisma-Spielwürfel
-
 Das One World Trade Center
Das One World Trade Center


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.04. 2024