Diagonale (Geometrie)

Diagonale (von altgriech. διά dia: „durch“ und γωνία gonia: „Ecke, Winkel“) ist ein Begriff aus der Geometrie. Allgemein bezeichnet der Begriff Strecken, die Ecken von Flächen oder Körpern miteinander verbinden, ohne selbst eine Seite bzw. Kante der Figur zu sein. Für die genaue Definition siehe unten.

Diagonalen in der ebenen Geometrie

Siebzehneck mit 14 Diagonalen aus einem Eckpunkt
z. B. bedeutet $d_{3}$ : Diagonale über drei Seiten

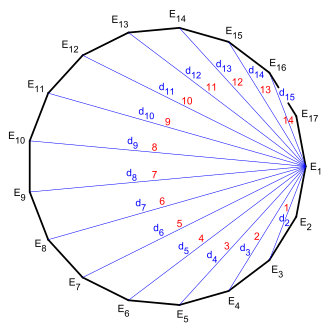
In der ebenen Geometrie bezeichnet man als Diagonalen die Verbindungsstrecken von nicht nebeneinander liegenden Ecken in einem Polygon (Vieleck), welches daher mindestens vier Ecken haben muss.

Anzahl der Diagonalen

Die Anzahl d(n) der Diagonalen in einem -Eck, also in einem Vieleck mit der Eckenzahl , beträgt

$d(n)={\frac {n(n-3)}{2}}$ ,

denn jede der Ecken wird mit n-3 Ecken durch eine Diagonale verbunden (nicht mit sich selbst und nicht mit den beiden Nachbarecken). Durch den Nenner (Divisor) 2 in der Formel wird berücksichtigt, dass mit dieser Betrachtung bei einem vollständigen Umlauf über alle Eckpunkte jede Diagonale zweimal erzeugt würde.

Daraus ergibt sich für die Eckenzahl 3 bis 25:

	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
	0	2	5	9	14	20	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275

Bei einem konvexen Polygon liegen alle Diagonalen vollständig innerhalb des Polygons, bei einem konkaven Polygon mindestens eine Diagonale komplett außerhalb.

Längen von Diagonalen

Allgemein

Die Diagonallänge von einer Ecke zur übernächsten Ecke berechnet sich aus der Länge der beiden dazwischenliegenden Seiten $s_{0}$ und $s_{1}$ und dem dazwischenliegenden Winkel $\varphi_1$ nach dem Kosinussatz:

$d = \sqrt{s_0^2+s_1^2-2s_0s_1\cos\varphi_1}$

Sind bei einer Diagonale für einen Teilumfang zwischen den Enden der Diagonale die Seiten und die Innenwinkel der dazwischenliegenden Ecken bekannt, so lässt sich die Diagonallänge daraus berechnen.

Bezeichnet man, von einem Diagonalenende ausgehend, die Seiten mit $s_{i}$ und den jeweils davor liegenden Innenwinkel mit $\varphi _{i}$ so gilt:

Für die Diagonale über drei Seiten:

$d_3 = \sqrt{(s_0-s_1 \cdot \cos(\varphi_1) + s_2 \cdot \cos(\varphi_1+\varphi_2))^2 + (s_1 \cdot \sin(\varphi_1) - s_2\cdot \sin((\varphi_1+\varphi_2))^2}$

Für die Diagonale über vier Seiten gilt:

${\begin{aligned}d_{4}^{2}&=(s_{0}-&s_{1}\cdot \cos(\varphi _{1})+s_{2}\cdot \cos(\varphi _{1}+\varphi _{2})-s_{3}\cdot \cos(\varphi _{1}+\varphi _{2}+\varphi _{3}))^{2}\\&+(&s_{1}\cdot \sin(\varphi _{1})-s_{2}\cdot \sin(\varphi _{1}+\varphi _{2})+s_{3}\cdot \sin(\varphi _{1}+\varphi _{2}+\varphi _{3}))^{2}\end{aligned}}$

Allgemein für eine Diagonale über Seiten:

$d_{n}={\sqrt {\left(s_{0}+\sum _{i=1}^{n-1}(-1)^{i}\cdot s_{i}\cdot \cos \left(\sum _{k=1}^{i}\varphi _{k}\right)\right)^{2}+\left(\sum _{i=1}^{n-1}-(-1)^{i}\cdot s_{i}\cdot \sin \left(\sum _{k=1}^{i}\varphi _{k}\right)\right)^{2}}}$

Spezialfälle

Für einige Spezialfälle existieren einfache Formeln für die Diagonalenlänge:

Die Diagonalenlängen eines Parallelogramms mit den Seitenlängen und sowie dem Innenwinkel $\alpha$ sind:

$e = \sqrt{a^2+b^2+2ab\cos\alpha}$

und

$f = \sqrt{a^2+b^2-2ab\cos\alpha}$

Für die Diagonalenlänge eines Rechtecks ( $\alpha =90^{\circ }$ ) mit den Seitenlängen und gilt daher nach dem Satz des Pythagoras:

$d = \sqrt{a^2+b^2}$ .

Regelmäßige Polygone

Die Diagonalenlänge eines Quadrats mit Seitenlänge lässt sich berechnen gemäß

$d = a\sqrt{2}$ .

Für die Diagonalenlänge eines regelmäßigen Fünfecks mit Seitenlänge gilt

$d = \frac{a}{2} \left(1+\sqrt{5}\right)$

Für die Diagonalen über zwei bzw. drei Seiten im regelmäßigen Sechseck mit Seitenlänge gilt

$d_2 = a \frac{\sqrt{3}}{2}$ sowie d_3 = 2 a

Allgemein ergibt sich in einem regelmäßigen Polygon mit Seitenlänge die Länge der Diagonale über Seiten als

$d_{k}=a\cdot \sin \left({\frac {k\pi }{n}}\right)\cdot \csc \left({\frac {\pi }{n}}\right)$ .

Diagonalen in der Raumgeometrie

In der Stereometrie versteht man unter der Diagonale eines Polyeders eine solche Strecke, die zwei Ecken des Körpers miteinander verbindet, aber weder mit einer Kante noch mit einer Diagonale einer Seitenfläche zusammenfällt (Raum- oder Körperdiagonale).

Anzahl der Diagonalen

Um die Anzahl der Diagonalen eines Polyeders zu finden, zieht man von der Zahl der Ecken den Wert 1 ab, multipliziert den Rest mit der Anzahl der Ecken und halbiert das Produkt. Von der so erhaltenen Zahl zieht man zunächst die Anzahl sämtlicher Kanten und dann die Anzahl der Diagonalen sämtlicher Seitenflächen ab.

Bezeichnet man die Eckenzahl mit , die Anzahl der Flächen mit die Anzahl der Kanten mit und die Anzahl der Ecken der Fläche Nr. mit $N_{i}$ einer so ergibt sich

$Z={\frac {E(E-1)}{2}}-K-\sum _{i=1}^{F}{\frac {N_{i}(N_{i}-3)}{2}}$

Für alle Parallelepipede, z.B. Quader, ergibt sich mit

$E = 8 , \quad F = 6 , \quad K = 12 , \quad N_i = 4 \quad \forall i$ :

$Z={\frac {8(8-1)}{2}}-12-\sum _{i=1}^{6}{\frac {4(4-3)}{2}}$

$Z = 28 - 12- 6 \cdot 2$

Längen von Diagonalen

Die Länge der Raumdiagonale eines Quaders (Seitenlängen , , ) beträgt $d = \sqrt{a^2+b^2+c^2}$ .

Für den Spezialfall des Würfels ergibt sich daraus $d = a\sqrt{3}$ .

Diagonalmethode

Anwendung in der Kunst

In der bildenden Kunst werden Diagonalen als Kompositionselement zur formalen Gestaltung von Werken genutzt. Insbesondere die Diagonalmethode teilt ein rechteckiges Format in zwei Quadrate und nutzt dann deren Diagonalen zur Bildanordnung.

Wahrnehmung

Diagonalen im weiteren Sinn der Kunst und (foto)grafischen Gestaltung werden unterschiedlich wahrgenommen: Jene, die im Verlauf nach rechts nach oben ansteigen werden als positiv und dynamisch rezipiert und daher als positive Diagonale bezeichnet. Den Gegenpol bildet die negative Diagonale die von links oben kommend im Bild nach rechts unten läuft – Symbol für bremsen, stoppen, negative Gefühle. Merkmal guter Gestaltung kann es sein, eine Diagonale oder diagonale Struktur die Bildaussage unterstützender Richtung aufzuweisen, eventuell gegenübergestellt mit einer kleinen Ausführung ihres Gegenstücks, einer Gegendiagonale. Erklärbar wird der Effekt wahrnehmungspsychologisch aus der Schreib- und Leserichtung nach rechts, der nach rechts oben verlaufenden Orientierung von schnell von Hand geschriebenen Buchstaben, kursiven Drucklettern, entsprechend der Unterarmbewegung nach rechts oben ansteigenden Zeilen von Handschrift und weiters Grafiken von Wissenschaft bis Börsenkurs, wenn sich über der nach rechts laufenden Zeitachse sich ein nach oben aufgetragener Wert positiv entwickelt.

Basierend auf einem Artikel in:

Wikipedia.de

	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
	0	2	5	9	14	20	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275

	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
	0	2	5	9	14	20	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275

	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
	0	2	5	9	14	20	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275