Schläfli-Symbol
Das Schläfli-Symbol, benannt nach dem Schweizer
Mathematiker Ludwig Schläfli,
wird in der Form
benutzt, um reguläre Polygone,
Polyeder
und andere Vielflächner, auch in höheren Dimensionen,
zu beschreiben.
Wenn
eine natürliche
Zahl ist, beschreibt das Symbol
ein regelmäßiges
Polygon (
-Eck).
Ist
ein nicht notwendig gekürzter
Bruch, dann beschreibt es
einen Stern.
Das Symbol
beschreibt eine Pflasterung
mittels regelmäßiger
-Ecke,
wobei
angibt, wie viele solcher Polygone an jeder Ecke
zusammenstoßen.
Die Inversion eines Schläfli-Symbols liefert das dazu duale Polygon.
Beispiele
Regelmäßige Polygone
bezeichnet ein
-Eck
Sterne
oder
bezeichnet das Pentagramm
vom Fünfeck
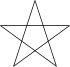
oder
und
oder
bezeichnen die zwei möglichen Heptagramme
vom Siebeneck
 und
und 
oder
bezeichnet das Oktogramm
vom Achteck

oder
und
oder
bezeichnen die zwei möglichen Enneagramme
vom Neuneck
 und
und 
oder
bezeichnet das Dekagramm vom Zehneck

oder
oder
oder
oder
bezeichnen die vier möglichen Hendekagramme vom Elfeck


 und
und 
oder
oder
oder
oder
oder
bezeichnen die fünf möglichen Tridekagramme vom Dreizehneck



 und
und 
oder
und
oder
bezeichnen die zwei möglichen Tetradekagramme vom Vierzehneck
 und
und 
oder
oder
sowie
oder
bezeichnen die drei möglichen Pentadekagramme vom Fünfzehneck

 und
und 
oder
oder
sowie
oder
bezeichnen die drei möglichen Hexadekagramme vom Sechzehneck

 und
und 
oder
oder
oder
oder
oder
oder
oder
bezeichnen die sieben möglichen Heptadekagramme vom Siebzehneck





 und
und 
oder
oder
oder
oder
oder
oder
oder
oder
bezeichnen die acht möglichen Enneadekagramme vom Neunzehneck






 und
und 
oder
oder
sowie
oder
bezeichnen die drei möglichen Ikosagramme vom Zwanzigeck

 und
und 
Platonische Körper
:
p ist die Zahl der Ecken des verwendeten Polygons; q ist die Zahl der an einer
Ecke zusammenstoßender Polygone
bezeichnet das selbstduale
Tetraeder.
bezeichnet das Oktaeder, die Inversion
den zum Oktaeder dualen Würfel.
bezeichnet das Ikosaeder,
die Inversion
das zum Ikosaeder duale Dodekaeder.
Platonische Parkette
bezeichnet die Dreieckparkettierung, die Inversion
die zur Dreieckparkettierung duale Sechseckparkettierung.
bezeichnet die selbstduale Quadratparkettierung.
- Das entscheidende Merkmal, worin sich das Schläfli-Symbol eines
Platonischen Körpers
von dem eines Platonischen Parketts
unterscheidet, ist, dass für einen Körper
gilt, für ein Parkett hingegen
.
Kepler-Poinsot-Körper
bezeichnet das Große
Ikosaeder, die Inversion
das zum Großen Ikosaeder duale Große
Sterndodekaeder.
bezeichnet das Große
Dodekaeder, die Inversion
das zum Großen Dodekaeder duale Kleine
Sterndodekaeder.
Vierdimensionale Körper
bezeichnet das Pentachoron,
den vierdimensionalen Würfel (Tesserakt),
das Duale
dazu den regulären
16-Zeller (Hexadekachor),
den regulären
24-Zeller (Ikositetrachor),
den regulären
120-Zeller, das Duale
dazu den regulären
600-Zeller.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.06. 2022