Würfel (Geometrie)
| Würfel | |
|---|---|

| |
| Art der Seitenflächen | Quadrate |
| Anzahl der Flächen | 6 |
| Anzahl der Ecken | 8 |
| Anzahl der Kanten | 12 |
| Schläfli-Symbol | {4,3} |
| dual zu | Oktaeder |
| Körpernetz | 
|
| Anzahl verschiedener Netze | 11 |
| Anzahl Kanten in einer Ecke | 3 |
| Anzahl Ecken einer Fläche | 4 |
Der Würfel (von deutsch werfen, weil er in Würfelspielen geworfen wird; auch regelmäßiges Hexaeder [hɛksaˈeːdər], von griech. hexáedron ‚Sechsflächner‘, oder Kubus, von altgriechisch κύβος kybos bzw. lat. cubus ‚Würfel‘) ist einer der fünf platonischen Körper, genauer ein dreidimensionales Polyeder (Vielflächner) mit
- 6 kongruenten Quadraten als Seitenflächen
- 12 gleich langen Kanten und
- 8 Ecken, in denen jeweils drei Seitenflächen zusammentreffen.
Der Würfel ist ein spezielles dreidimensionales Parallelepiped, ein spezieller, nämlich gleichseitiger Quader sowie ein spezielles gerades quadratisches Prisma. Die Größen eines Würfels werden bereits durch die Angabe eines Wertes, Kantenlänge, Flächendiagonale, Raumdiagonale, Oberflächeninhalt oder Volumen, festgelegt.
Symmetrie

mit Beispielen der Drehachsen
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Seiten sind untereinander gleichartig – ist der Würfel ein reguläres Polyeder. Er hat
- 3 vierzählige Drehachsen
(durch die Mittelpunkte zweier gegenüberliegender Flächen),
- 4 dreizählige Drehachsen
(durch zwei diagonal gegenüberliegende Ecken),
- 6 zweizählige Drehachsen
(durch die Mittelpunkte zweier diagonal gegenüberliegender Kanten),
- 9 Spiegelebenen (6 Ebenen durch jeweils vier Ecken (z.B. grün), 3 Ebenen durch je vier Kantenmittelpunkte (z.B. rot)),
- 14 Drehspiegelungen (6 um 90° mit den Ebenen durch je vier Kantenmittelpunkte und 8 um 60° mit Ebenen durch je sechs Kantenmitten)
und ist
- punktsymmetrisch zum Mittelpunkt M.
Für eine vierzählige Drehachse gibt es 3
Symmetrieoperationen
(Drehung um 90°, 180° und 270°), für eine dreizählige Drehachse dementsprechend 2 Symmetrieoperationen.
Insgesamt hat die Symmetriegruppe des Würfels 48 Elemente. Man bezeichnet sie in der
Notation von Schoenflies als
,
in der Notation von Hermann /
Mauguin als
oder allgemein aber etwas ungenau als Oktaedergruppe bzw.
Würfelgruppe.
Konstruktion

Euklid beschreibt und beweist im dreizehnten Buch seines Werkes Elemente, unter Proposition 15, die Konstruktion des Würfels.
„Einen Würfel einer Kugel mit gegebenem Durchmesser einbeschreiben.
Das Quadrat über dem Durchmesser der Kugel ist dann gleich dem dreifachen
Quadrat über der Kante des Würfels.“
„Rudolf Haller“
Um den Aufwand zu minimieren, enthält die folgende sphärischen Darstellung nur die Schritte, die für den Würfel vonnöten sind. Von Vorteil ist hierzu die Anwendung einer sogenannten Dynamische-Geometrie-Software (DGS).
Gegeben sei eine Umkugel mit dem Radius gleich
.
Beim Bestimmen der
und
Achsen eines kartesischen Koordinatensystems ergeben sich die
Punkte
und
auf der Oberfläche der Umkugel.
Vorab ist aus einem rechtwinkligen Dreieck die Kantenlänge
des Würfels zu ermitteln. Hierzu wird zuerst der Umkreisbogen
eingezeichnet.
Das anschließend konstruierte rechtwinklige Dreieck
liefert mit der Kathete
als Hypotenuse die Kantenlänge
des Würfels.
Die eigentliche Konstruktion des Würfels beginnt mit dem Einzeichnen des Inkreises
des Würfels um Mittelpunkt
mit Radius
und Richtung
Achse. Die Schnittpunkte sind
und
.
Eine Parallele zur
Achse durch Punkt
und eine Parallele zur
Achse durch Punkt
schneiden sich in
.
Es folgt der Kreis
um
mit Richtung parallel zur
Achse. Die sich anschließende Parallele zur
Achse durch
erzeugt die beiden ersten Eckpunkte
und
.
Mit der Verbindung dieser beiden Punkte ergibt sich die erste Kante
des Würfels.
Es geht weiter mit dem Kreis
um
mit Richtung parallel zur
Achse und der darauffolgenden Parallelen zur
Achse durch
entsteht die nächste Kante
.
Eine Parallele zu
durch
und eine weitere Parallele zu
durch
vervollständigt die Vorderseite
des entstehenden Würfels.
Zieht man nun eine Parallele zur
Achse durch
ergibt sich mit dem Schnittpunkt
die Kante
.
Mithilfe sechs weiterer Parallelen zu den betreffenden Kanten erhält man die noch fehlenden drei Eckpunkte
und
für den fertigen Würfel
.
Beziehungen zu anderen Polyedern

Der Würfel ist das zum Oktaeder duale Polyeder und umgekehrt. Außerdem beschreiben die Eckpunkte des Würfels zwei punktsymmetrische reguläre Tetraeder, welche zusammen das Sterntetraeder als weiteres reguläres Polyeder bilden.
Mithilfe von Würfel und Oktaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Würfelgruppe als Symmetriegruppe haben. So erhält man zum Beispiel
- den Hexaederstumpf bzw. den abgestumpften Würfel mit 6 Achtecken und 8 Dreiecken
- das Kuboktaeder mit 6 Quadraten und 8 Dreiecken, also 14 Seiten, und 12 Ecken
- den Oktaederstumpf bzw. das abgestumpfte Oktaeder mit 6 Quadraten und 8 Sechsecken
als Durchschnitte eines Würfels mit einem Oktaeder (siehe archimedische Körper) und
- das Rhombendodekaeder mit 6 + 8 = 14 Ecken und 12 Rauten als Seiten
als konvexe Hülle einer Vereinigung eines Würfels mit einem Oktaeder.
Der Würfel ist Baustein der regulären Würfelparkettierung.
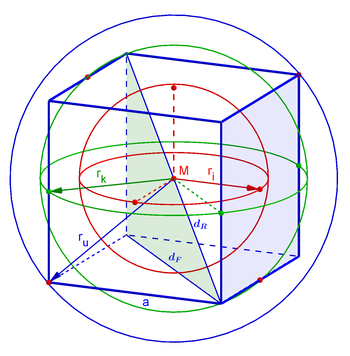
Formeln
| Größen eines Würfels mit Kantenlänge a | ||
|---|---|---|
| Volumen |
| |
| Mantelfläche | ||
| Oberflächeninhalt | ||
| Umkugelradius | ||
| Kantenkugelradius | ||
| Inkugelradius | ||
| Raumdiagonale | ||
| Flächendiagonale | ||
| Verhältnis von Volumen zu Umkugelvolumen |
||
| Winkel zwischen benachbarten Flächen/Kanten |
||
| Raumwinkel in den Ecken | ||
| Sphärizität | ||
Raumwinkel in den Ecken
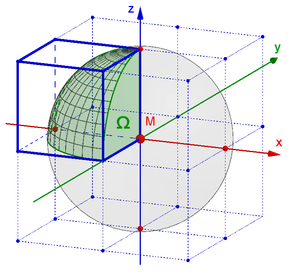
Dieser Raumwinkel
ergibt sich sehr einfach aus der Betrachtung folgender Gegebenheit.
Für den dreidimensionalen Raum wird ein kartesisches Koordinatensystem verwendet, das den Raum in 8 Oktanten einteilt. Darin ist der 0-Punkt der drei Koordinatenebenen (x, y, z) der Treffpunkt 8 virtueller Würfel. Mit dem 0-Punkt als Mittelpunkt der
Einheitskugel, hat der Raumwinkel (Vollwinkel) den Wert
Betrachtet man vom 0-Punkt ausgehend nur 1 Würfel, so ist folglich sein Raumwinkel
Umgeformt und mit einer Maßeinheit bezeichnet gilt
Definition als Menge von Punkten
Der Würfel kann als Menge von Punkten
im dreidimensionalen euklidischen Raum definiert werden, wo die absoluten Beträge der 3 Koordinaten im
kartesischen Koordinatensystem höchstens so groß ist wie der
Inkugelradius
. Formal lässt sich diese Menge aufschreiben als
Dabei ist die Maximumsnorm oder Unendlich-Norm des
Vektors
.
Für das Innere des Würfels gilt
und für die Oberfläche gilt
. Nach dieser Definition ist der Mittelpunkt
des Würfels der Koordinatenursprung und seine Kanten und Seitenflächen verlaufen parallel zu den 3 Achsen des kartesischen Koordinatensystems.
Allgemeiner kann ein Würfel, der eine beliebige Lage im dreidimensionalen
euklidischen Raum hat, mithilfe von Vektoren
definiert werden. Ist
der Ortsvektor des
Mittelpunkts und sind
,
,
orthogonale Richtungsvektoren, die den Mittelpunkt
des Würfel mit den Mittelpunkten von 3 Seitenflächen verbinden, also
Normalenvektoren der 3 Seitenflächen sind und ein
Orthogonalsystem des dreidimensionalen Vektorraums
bilden, dann lässt sich die Menge der Punkte des Würfels definieren als die Menge der Vektoren
Verallgemeinerung
Auch die Verallgemeinerungen des Würfels in beliebiger Dimension
werden als
-dimensionale
Würfel oder Hyperwürfel bezeichnet und sind ebenfalls reguläre
Polytope. Der
-dimensionale
Würfel hat
begrenzende Seiten der Dimension k. Spezialfälle:
- Der nulldimensionale Würfel (Punkt) hat 1 Ecke.
- Der eindimensionale Würfel (Strecke) hat 2 Ecken.
- Der zweidimensionale Würfel (Quadrat) hat 4 Ecken und 4 Kanten
- Der vierdimensionale Hyperwürfel (Tesserakt) hat 16 Ecken, 32 Kanten, 24 Seitenquadrate und 8 Seitenwürfel.
- Der
-dimensionale Hyperwürfel hat
Ecken (
)
Kanten (
)
Quadrate als Flächen (
)
Würfel als Volumen (
)
Hyperwürfel der Dimension
als Facetten (
).
Ein Modell für den -dimensionalen Würfel ist der Einheitswürfel
im Vektorraum
. Und zwar ist der abgeschlossene Einheitswürfel
, das
-fache kartesische Produkt des Einheitsintervalls
- die konvexe Hülle der
Eckpunkte mit den Koordinaten
und
- der Durchschnitt der
Halbräume
und
Der Einheitswürfel ist ein achsenparalleler Würfel mit der Kantenlänge
und einer Ecke im
Koordinatenursprung. Eine Verallgemeinerung dieses Konzepts sind
Quader im
,
die in der mehrdimensionalen Analysis eine Rolle spielen.
Netze des Würfels
Der Würfel hat elf Netze (siehe Abbildung). Diese sind bestimmte Hexominos. Das heißt, es gibt elf Möglichkeiten, einen hohlen Würfel durch Aufschneiden von 7 Kanten aufzuklappen und in der Ebene auszubreiten. Die anderen 5 Kanten verbinden jeweils die 6 Quadrate des Netzes. Um einen Würfel so zu färben, dass keine benachbarten Flächen dieselbe Farbe haben, braucht man mindestens 3 Farben.


Graphen, duale Graphen, Zyklen, Färbungen
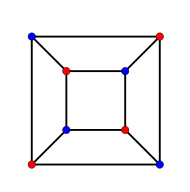
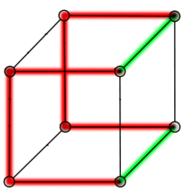
Der Würfel hat einen ihm zugeordneten ungerichteten planaren Graphen mit 8 Knoten, 12 Kanten und 6 Gebieten, der 3-regulär ist, d.h. von jedem Knoten gehen 3 Kanten aus, sodass der Grad für alle Knoten gleich 3 ist. Bei planaren Graphen ist die genaue geometrische Anordnung der Knoten unwesentlich. Wichtig ist allerdings, dass sich die Kanten nicht schneiden müssen. Die Knoten dieses Würfelgraphen entsprechen den Ecken des Würfel.

Würfel umschreibt dualen Oktaeder
Die Knoten des Würfelgraphen können mit 2 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind. Bei dieser alternierenden Knotenfärbung wechselt die Farbe hin und her, wenn von einem Knoten zu einem benachbarten gegangen wird. Dies bedeutet, dass die chromatische Zahl dieses Graphen gleich 2 ist. Außerdem können die Kanten mit 3 Farben so gefärbt werden, dass benachbarte Kanten immer unterschiedlich gefärbt sind (siehe Abbildung). Mit 2 Farben ist das nicht möglich, sodass der chromatische Index für die Kantenfärbung gleich 3 ist (das nebenstehende Bild veranschaulicht diese Färbungen).
Um die entsprechende nötige Anzahl der Farben für die Flächen oder Gebiete zu bestimmen, ist der duale Graph (Oktadergraph) mit 6 Knoten, 12 Kanten und 8 Gebieten hilfreich. Die Knoten dieses Graphen werden dabei den Gebieten des Würfelgraphen eineindeutig (bijektiv) zugeordnet und umgekehrt (siehe bijektive Funktion und Abbildung oben). Die Knoten des Oktadergraphen können mit 3 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind, aber nicht mit 2 Farben, sodass die chromatische Zahl des Oktadergraphen gleich 3 ist. Daraus lässt sich indirekt schließen: Weil die chromatische Zahl gleich 3 ist, sind 3 Farben für eine solche Flächenfärbung des Würfels oder eine Färbung der Gebiete des Würfelgraphen nötig.

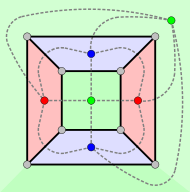
Die 7 aufgeschnittenen Kanten jedes Netzes (siehe oben) bilden zusammen mit den Ecken (Knoten) einen Spannbaum des Würfelgraphen. Jedes Netz entspricht genau einem Spannbaum und umgekehrt, sodass hier eine eineindeutige (bijektive) Zuordnung zwischen Netzen und Spannbäumen besteht. Wenn man ein Würfelnetz ohne das äußere Gebiet als Graphen betrachtet, erhält man als dualen Graphen jeweils einem Baum mit 6 Knoten und 5 Kanten und dem maximalen Knotengrad 4. Jede Fläche des Würfels wird dabei einem Knoten des Baums zugeordnet. Dabei kommt jede graphentheoretische Konstellation (siehe Isomorphie von Graphen) solcher Bäume vor, einige auch mehrfach.
Der Würfelgraph besitzt 12 Hamiltonkreise, aber keine Eulerkreise.
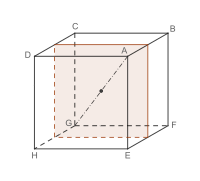
Schnittflächen des Würfels
Wenn ein Würfel von einer Ebene geschnitten wird, kann als Schnittfläche ein Dreieck, Viereck, (unregelmäßiges) Fünfeck oder Sechseck entstehen. Als Schnittfläche ist auch ein gleichseitiges Dreieck, ein Quadrat oder ein regelmäßiges Sechseck möglich.
Eine Schnittfläche in der Form eines regelmäßigen Fünfecks – keine parallele Seiten – ist nicht machbar, da im Würfel jeweils zwei Flächen parallel zueinander stehen.
-
 Gleichseitiges Dreieck als Schnittfläche
Gleichseitiges Dreieck als Schnittfläche -
 Quadrat als Schnittfläche
Quadrat als Schnittfläche -
 Regelmäßiges Sechseck als Schnittfläche
Regelmäßiges Sechseck als Schnittfläche -
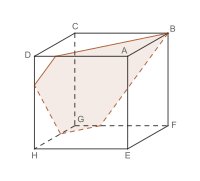 Unregelmäßiges Fünfeck als Schnittfläche
Unregelmäßiges Fünfeck als Schnittfläche
Würfelgitter

Das Würfelgitter ist eine Anordnung von unendlich vielen Punkten im dreidimensionalen euklidischen Raum. Diese Punkte können als alle Punkte im dreidimensionalen kartesischen Koordinatensystem aufgefasst werden, wo alle 3 Koordinaten ganze Zahlen sind. Diese Punktmenge kann formal als die Menge
geschrieben werden.
Dieses Würfelgitter ist achsensymmetrisch,
drehsymmetrisch und
punktsymmetrisch, besitzt also alle
Symmetrien der Oktaedergruppe bzw. Würfelgruppe. Außerdem ist es translationsymmetrisch
für alle Vektoren mit ganzzahliger Länge,
die parallel zu den 3 Koordinatenachsen verlaufen, also die unendlich vielen Vektoren
,
,
,
wobei
,
,
ganze Zahlen sind und
,
,
die 3
Einheitsvektoren im dreidimensionalen eudklidischen Vektorraum.
Solche Betrachtungen spielen in der Kristallographie eine wichtige Rolle. Das Würfelgitter entspricht dem kubischen Kristallsystem.
Werden unendlich viele parallele Ebenen, die jeweils den Abstand 1 haben, orthogonal zu den 3 Koordinatenachsen durch dieses kubische Punktgitter gelegt, dann entsteht ein kubisches Flächengitter (siehe Abbildung). Diese Ebenen können formal als die Menge
geschrieben werden.
Wird zusätzlich der dreidimensionale Raum vollständig ausgefüllt, dann entsteht eine dreidimensionale Parkettierung (Raumfüllung) aus kongruenten Würfeln mit gleicher Kantenlänge (siehe Raumfüllungen mit Würfeln).
Würfelverdoppelung
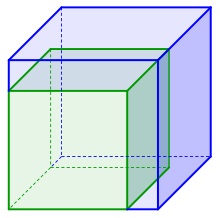
Die Würfelverdoppelung, auch bekannt als Delisches Problem, bezeichnet die geometrische Aufgabe, für einen gegebenen Würfel einen zweiten Würfel zu konstruieren, der im Vergleich zum ersten Würfel das doppelte Volumen aufweist. Das Problem gehört zu den drei „klassischen Problemen der antiken Mathematik“ und wurde bereits im 5. Jahrhundert v. Chr. im Antiken Griechenland formuliert.
Versucht man das Problem ausschließlich mit den Hilfsmitteln zu bearbeiten, die Euklid in seinen Elementen nutzt, nämlich mit Zirkel und unmarkiertem Lineal, ist es nicht lösbar. Dies bewies der französische Mathematiker Pierre Wantzel im Jahr 1837. Schwächt man diese Einschränkung ab und lässt ein zusätzliches Hilfsmittel zu, wie zum Beispiel eine entsprechende Markierung auf dem Lineal oder spezielle Kurven, ist die Konstruktion eines Würfels mit doppeltem Volumen möglich. An solchen Lösungsmöglichkeiten war bereits in der Antike eine gewisse Zahl bekannt.
Raumfüllungen mit Würfeln
Der dreidimensionale euklidische Raum kann lückenlos mit platonischen Körpern oder in Kombination mit archimedischen Körpern (und Prismen) gleicher Kantenlänge ausgefüllt werden kann. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt. Die folgenden Raumfüllungen enthalten Würfel:
-
 Raumfüllung mit Würfel
Raumfüllung mit Würfel -
 Raumfüllung mit Rhombenkuboktaeder, Kuboktaeder und Würfel
Raumfüllung mit Rhombenkuboktaeder, Kuboktaeder und Würfel -
 Raumfüllung mit Rhombenkuboktaeder, Würfel und Tetraeder
Raumfüllung mit Rhombenkuboktaeder, Würfel und Tetraeder -
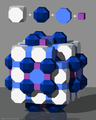 Raumfüllung mit Hexaederstumpf, Rhombenkuboktaeder, Achteckprisma und Würfel
Raumfüllung mit Hexaederstumpf, Rhombenkuboktaeder, Achteckprisma und Würfel -
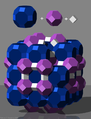 Raumfüllung mit Großem Rhombenkuboktaeder, Oktaederstumpf und Würfel
Raumfüllung mit Großem Rhombenkuboktaeder, Oktaederstumpf und Würfel
Beziehungen zu anderen Raumfüllungen
Der Würfel bzw. das regelmäßige Hexaeder ist der einzige platonische Körper, mit dem eine Raumfüllung aus ausschließlich kongruenten Polyedern möglich ist. Die Ecken dieser gleich großen Würfel bilden dann ein Würfelgitter. Diese Raumfüllung steht in Zusammenhang mit zwei anderen Raumfüllungen, die nur aus einer Art von kongruenten Polyedern bestehen: Die Raumfüllung aus Oktaederstümpfen und die Raumfüllung aus Rhombendodekaedern.
Wird eine alternierende halbe Raumfüllung mit Würfeln der Kantenlänge
genommen,
also jeder 2. Würfel der Raumfüllung, und jeweils eine quadratische Pyramide mit einem
Quadrat der Seitenlänge
und der
Höhe
nach außen auf alle quadratischen Seitenflächen der Würfel gesetzt, dann entstehen
kongruente Rhombendodekaeder,
die den Raum vollständig ausfüllen. Der Diederwinkel an der Grundfläche der
quadratische Pyramiden beträgt
, der gesamte an den 12 Kanten der Würfel entstehende
Winkel also
. Daher bilden die an den Kanten des Würfels liegenden 24
gleichschenkligen Dreiecke 12 Rauten und ein Rhombendodekaeder
entsteht. Nach dem Satz des Pythagoras haben diese Rhombendodekaeder
die Kantenlänge
und offensichtlich das Volumen
. Mit Hilfe der Formel für das Volumen der
quadratischen Pyramide ergibt sich ebenfalls
.
Werden stattdessen aus der alternierenden halben Raumfüllung nur die Würfel aus alternierenden Reihen –
egal entlang welcher der 3 Dimensionen – genommen, also jeder 4. Würfel der ursprünglichen Raumfüllung,
jeweils ein im Winkel von 45° auf der Spitze stehendes Quadrat mit halbem Flächeninhalt in der Mitte zwischen zwei
benachbarten Würfeln derselben Schicht platziert, und die Ecken dieser Quadrate, die jeweils den kleinsten
Abstand zueinander haben, mit Kanten verbunden, dann entstehen
kongruente
Oktaederstümpfe mit jeweils 6 Quadraten
und 8 regelmäßigen
Sechsecken als Seitenflächen,
die den Raum vollständig ausfüllen. Die Mittelpunkte der entstandenen regelmäßigen Sechsecke sind die Ecken der ursprünglichen Würfel. Die Ecken der
quadratischen Seitenflächen der
Oktaederstümpfe sind Seitenmitten von "unsichtbaren" Quadraten mit der Seitenlänge
.
Die Oktaederstümpfe haben also die Kantenlänge
und offensichtlich das Volumen
. Mit Hilfe der Formel für das Volumen der quadratischen Pyramide
ergibt sich ebenfalls
.
-
 Raumfüllung mit Würfeln
Raumfüllung mit Würfeln -
 Aus der alternierenden halben Raumfüllung mit Würfeln entsteht eine Raumfüllung aus kongruenten Rhombendodekaedern
Aus der alternierenden halben Raumfüllung mit Würfeln entsteht eine Raumfüllung aus kongruenten Rhombendodekaedern -
 Aus der alternierenden geviertelten Raumfüllung mit Würfeln entsteht eine Raumfüllung aus kongruenten Oktaederstümpfen
Aus der alternierenden geviertelten Raumfüllung mit Würfeln entsteht eine Raumfüllung aus kongruenten Oktaederstümpfen
Handwerkliches
Gesteckter Würfel
Aus über hundert Zündhölzern lassen sich rein durch Klemmen und Reibung zusammenhaltende Würfel fertigen.
-
Streichholzwürfel
-
 Origami-Würfel
Origami-Würfel
Origami
Mit Hilfe der Origami-Technik lässt sich aus einzelnen Papierblättern ohne Klebstoff ein Würfel basteln.
Drehmaschine
Auf einer Drehbank zur spanabhebenden Metallbearbeitung lässt sich mittels 4-Backen-Futter oder einer schonenden rohrförmigen Halterung auch im 3-Backen-Futter ein Würfel herstellen. Das Drehen einer Kombination von bis zu vier losen, doch unverlierbar ineinander liegenden Würfeln ist eine Geschicklichkeitsaufgabe. Dieses Werkstück wird im Englischen als turner’s cube, also ‚Würfel des Drehers‘ bezeichnet. Die drei äußeren Würfel haben dabei in jeder Seitenfläche eine große Bohrung, die als Fenster die Sicht auf die oder den innen nächst folgenden erlaubt. Die Größen der drei inneren Würfel sind abgestuft genau so gestaltet, dass schon die Flächendiagonale nicht durch diese Bohrung des jeweils nächstgrößeren passt. Nötig ist das Hinterschneiden bei der Bearbeitung von jeder Seite der innenliegenden Würfel und das temporäre Fixieren mit Klebstoff oder Wachs, wenn zuletzt die sechsten Seiten bearbeitet werden.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.08. 2023