
Regulärer Graph
In der Graphentheorie heißt ein Graph regulär, falls alle seine Knoten gleich viele Nachbarn haben, also den gleichen Grad besitzen. Bei einem regulären gerichteten Graphen muss weiter die stärkere Bedingung gelten, dass alle Knoten den gleichen Eingangs- und Ausgangsgrad besitzen. Ein regulärer Graph mit Knoten vom Grad k wird k-regulär oder regulärer Graph vom Grad k genannt.
Reguläre Graphen mit einem Grad von höchstens 2 lassen sich leicht klassifizieren: Ein 0-regulärer Graph besteht aus unzusammenhängenden Knoten, ein 1-regulärer Graph besteht aus unzusammenhängenden Kanten, und ein 2-regulärer Graph besteht aus unzusammenhängenden Kreisen.
Ein 3-regulärer Graph wird auch als kubischer Graph bezeichnet.
Ein stark regulärer Graph ist ein regulärer Graph, bei dem je 2 benachbarte Knoten genau a gemeinsame Nachbarn, und je zwei nicht benachbarte Knoten genau b gemeinsame Nachbarn haben. Der kleinste reguläre, aber nicht stark reguläre Graph ist der Kreisgraph und der zirkuläre Graph mit je 6 Knoten.
Der vollständige
Graph
ist für jedes
stark regulär.
Nach einem Satz von Nash-Williams
hat jeder k-reguläre Graph mit
Knoten einen Hamiltonkreis.
-
 0-regulärer Graph
0-regulärer Graph -
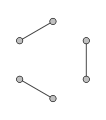 1-regulärer Graph
1-regulärer Graph -
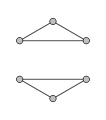 2-regulärer Graph
2-regulärer Graph -
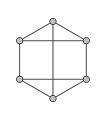 3-regulärer Graph
3-regulärer Graph
Algebraische Eigenschaften
Sei A die Adjazenzmatrix
eines Graphen. Der Graph ist genau dann regulär, wenn
ein Eigenvektor
von A ist.
Der Eigenwert
dieses Vektors ist gleichbedeutend mit dem Grad des Graphen. Eigenvektoren mit
anderen Eigenwerten sind orthogonal
zu
,
d.h. für solche Eigenvektoren
gilt:
.
Ein regulärer Graph vom Grad k ist genau dann zusammenhängend, wenn der Eigenwert k die Vielfachheit eins hat.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.10. 2020