Rhombenkuboktaeder

3D-Ansicht eines Rhombenkuboktaeders

Körpernetz eines Rhombenkuboktaeders

Älteste gedruckte Darstellung eines Rhombenkuboktaeders aus Leonardo da Vincis Divina Proportione

Straßenbeleuchtung vor dem Mainzer Dom

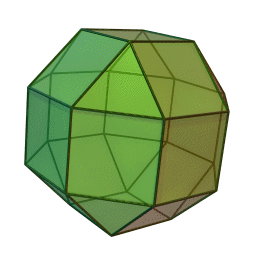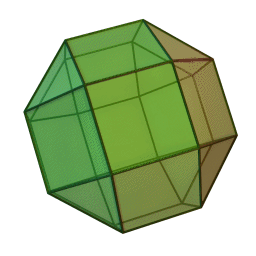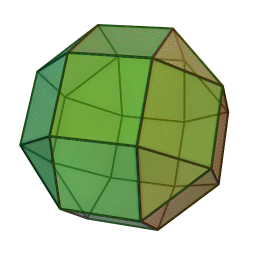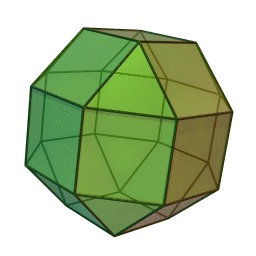
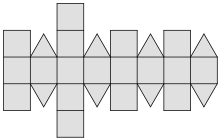
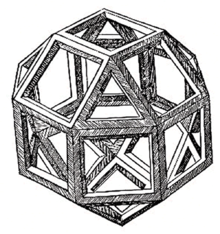
Das (kleine) Rhombenkuboktaeder ist ein Polyeder (Vielflächner), das zu den archimedischen Körpern zählt. Es setzt sich aus 8 gleichseitigen Dreiecken und 18 Quadraten zusammen. Dabei bilden jeweils drei Quadrate und ein Dreieck eine Raumecke.

Jeweils 8 Kanten des Rhombenkuboktaeders bilden die Kanten eines regelmäßigen Achtecks. Insgesamt gibt es sechs solcher unabhängiger, gleichseitiger Achtecke in diesem Polyeder.

Der Name des Rhombenkuboktaeders beruht u.a. auf der Tatsache, dass 12 der 18 Quadrate deckungsgleich zu den 12 Rhomben eines umbeschriebenen Rhombendodekaeders sind. Der zum Rhombenkuboktaeder duale Körper ist das Deltoidalikositetraeder.

Formeln

Größen eines Rhombenkuboktaeders mit Kantenlänge a
Volumen ≈ 8,71 a³	$V={\frac {2}{3}}\,a^{3}\left(6+5{\sqrt {2}}\right)$
Oberflächeninhalt ≈ 21,46 a²	$A_{O}=2\,a^{2}\left(9+{\sqrt {3}}\right)$
Umkugelradius ≈ 1,4 a	$R={\frac {a}{2}}{\sqrt {5+2{\sqrt {2}}}}$
Kantenkugelradius ≈ 1,31 a	$r={\frac {a}{2}}{\sqrt {4+2{\sqrt {2}}}}$
Flächenwinkel (Quadrat–Quadrat) = 135°	$\cos \,\alpha _{1}=-{\frac {1}{2}}{\sqrt {2}}$
Flächenwinkel (Quadrat–Dreieck) ≈ 144° 44′ 8″	$\cos \,\alpha _{2}=-{\sqrt {{\frac {2}{3}}}}$
Eckenraumwinkel ≈ 1,108 π	$\Omega =2\pi -\arccos \left(-{\frac {2}{3}}{\sqrt {2}}\right)$
Sphärizität ≈ 0,95408	$\Psi ={\frac {\sqrt[{3}]{32\,\pi \left(43+30{\sqrt {2}}\right)}}{2\left(9+{\sqrt {3}}\right)}}$

Trivia

In der Technik wird die Form bei Bauteilen verwendet, die als Knoten zum Aufbau von metallenem Raumfachwerk dienen.

Das Rhombenkuboktaeder bildet den Grundkörper des als Advents- und Weihnachtsstern weit verbreiteten Herrnhuter Sterns.

Die Nationalbibliothek von Belarus ist in Form eines Rhombenkuboktaeders erbaut.

Siehe auch

Pseudo-Rhombenkuboktaeder

Basierend auf einem Artikel in:

Wikipedia.de