Diederwinkel

Der Dieder- oder Torsionswinkel beschreibt in der Geometrie den Winkel zwischen zwei Flächen; dies gilt insbesondere innerhalb einer chemischen Verbindung für den Winkel zwischen zwei gedachten Flächen. Dabei wird der Diederwinkel α durch vier Atome und ihre Positionen zueinander definiert; er entspricht im Beispiel der organischen Verbindung Ethan dem Winkel, den die beiden durch $RCC$ und $CCR^{\prime }$ aufgespannten Ebenen zueinander einnehmen, wie in nachstehender Abbildung dargestellt ( und sind die beiden Kohlenstoffatome, und $R^{\prime }$ zwei beliebige Wasserstoffatome):

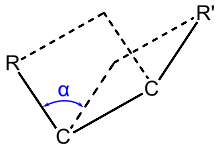
Graphische Darstellung des Diederwinkels $\alpha$ im Ethan; analog ist die Situation etwa bei Wasserstoffperoxid $H_{2}O_{2}$ , hier wäre die Bindungsachse O–O, R und R' wieder je ein Wasserstoffatom, der Diederwinkel $\alpha =111,5^{o}$

Sind die beiden Kohlenstoffatome durch eine Einfachbindung (σ-Bindung) verbunden und nicht in einem cyclischen Molekül arretiert, kann der Diederwinkel kontinuierlich alle Werte von 0° bis 180° annehmen. Aufgrund von abstoßenden Wechselwirkungen der Substituenten und $R^{\prime }$ ist in der Regel ein Winkel von $\alpha =180^{o}$ (trans, s.u.) am günstigsten.

Die Tatsache, dass viele Zucker unerwarteterweise eine Konformation einnehmen, in der einige Substituenten einen Diederwinkel von $\alpha =120^{o}$ bevorzugen, wird dem anomeren Effekt zugeschrieben.

Die mit der Drehung um die Bindung variierende Enthalpie des Moleküls kann durch eine spezielle Funktion angenähert berechnet werden:

$E = A \left(1 + \cos \alpha \right) + B \left(1 - \cos 2\alpha \right) + C \left(1 + \cos 3\alpha \right)$

mit E: Torsionsenergie; A, B, C: Skalierungsfaktoren; α: Diederwinkel

Die sich aus dieser Funktion ergebende Potentialkurve (angenähert mit Werten für A,B und wie bei n-Butan) sei zur Illustration unten abgebildet.

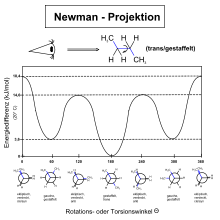
Energieunterschiede im Butan in Abhängigkeit vom Diederwinkel

Im Falle des Ethans werden A und B Null, wodurch die Gleichung in das Pitzer-Potential übergeht. Die Rotationsbarrieren liegen in der Regel bei wenigen kJ/mol. Dies bedeutet, dass immer ein kleiner Teil (< 20 %) der Moleküle einen Diederwinkel von $\alpha =0^{o}$ aufweisen. Dabei muss noch berücksichtigt werden, dass die gauche-Formen einen Entropie-Vorteil von 1,7 kJ/mol haben, da sie in zwei Rotationsisomeren (+/− synklinal) auftreten. Die für bestimmte Werte des Diederwinkels entstehenden Konformere haben eigene Bezeichnungen:

Winkel	Form	Explizite Beschreibung	Kurzbezeichnung
α = 0°	ekliptisch, verdeckt	syn-periplanar	cis/syn
α = 60°	gestaffelt	(+)-synklinal	gauche
α = 120°	ekliptisch, verdeckt	(+)-antiklinal	–
α = 180°	gestaffelt	antiperiplanar	trans/anti
α = 240°	ekliptisch, verdeckt	(−)-antiklinal	–
α = 300°	gestaffelt	(−)-synklinal	gauche
α = 360°	ekliptisch, verdeckt	syn-periplanar	cis/syn

Die Formen mit $\alpha =60^{o}$ respektive $300^{o}$ sind Enantiomere. Ist die Rotationsbarriere zu hoch, sind die beiden sich ergebenden Formen nicht in der Lage, durch Rotation ineinander überzugehen. Sie können dann unter Umständen einzeln isoliert werden. Dies wird im Fall von speziellen Binaphthylderivaten genutzt, um außerordentlich selektive Reagenzien zu gewinnen.

Falls zwischen den Kohlenstoffatomen eine Doppelbindung existiert, ist die Rotation stark eingeschränkt, da hierfür ein Bindungsbruch erfolgen müsste. Es sind nur zwei Winkel möglich: $\alpha =180^{o}$ (trans/anti) und $\alpha =0^{o}$ (cis). Sind die Substituenten sehr voluminös, kann es in letzterem Fall aber zu Abweichungen von dem 0°-Winkel kommen.

Zur Bestimmung der Diederwinkel realer Verbindungen stehen verschiedene Methoden zur Verfügung. Dazu gehören die Messung des Dipolmomentes, die Aufnahme von Elektronenbeugungsspektren, die Messung von Kopplungskonstanten mittels NMR oder die Berechnung der optimalen Molekülgeometrie mittels spezieller Computerprogramme.

Torsionswinkel in Proteinen

Die Torsionswinkel ω, φ und ψ des Backbones von Proteinen

Die Torsionswinkel des Backbones von Proteinen werden

ω (zwischen C^α − C' − N − C^α)
φ (zwischen C' − N − C^α − C')
ψ (zwischen N − C^α − C' − N) und

genannt. Dadurch kontrolliert der φ-Winkel den Abstand zweier Carbonyl-Kohlenstoffatomen, ψ den Abstand zweier Amid-Stickstoffe und ω den Abstand zweier α-Kohlenstoffe.

Die Planarität der Peptidbindung zwingt den ω-Winkel normalerweise auf 180° (die häufige trans-Konformation) oder 0° (die seltene cis-Konformation). Der Abstand zwischen den α-Kohlenstoffatomen beträgt in der trans- und cis-Konformation etwa 3,8 bzw. 2,8 Å. Die cis-Konformation ist hauptsächlich in der X-Pro-Peptidbindung zu beobachten (X ist eine beliebige Aminosäure), daher gilt Prolin neben dem achiralen Glycin als Strukturbrecher. Die Diederwinkel φ und ψ eines Proteins werden im Ramachandran-Plot dargestellt und sollten zu über 80 % in den Kernbereichen und höchstens vereinzelt in den verbotenen Bereichen der Karte liegen. Bei den besonders günstigen α-Helices z.B. liegt der φ-Winkel etwa bei −60°, der ψ-Winkel etwa bei −30°, wobei beide Winkel eine Toleranz von etwa ±30° zulassen.

Die Torsionswinkel der Seitenketten werden mit χ₁ bis χ₅ bezeichnet, abhängig vom Abstand zum Backbone. χ₁ ist der Torsionswinkel zwischen den Atomen N − C^α − C^β − C^γ, χ₂ zwischen C^α − C^β − C^γ − C^δ etc.

Die Seitenkettentorsionswinkel scheinen sich um die 180°, 60° und −60° zu häufen. Diese Konformationen werden als anti (oder trans), (+)-gauche und (−)-gauche (oder (+)- bzw. (−)-synklinal) bezeichnet. Welcher Torsionswinkel in einer Seitenkette vorliegt, wird durch Dieder benachbarter Seitenketten und des Backbones bestimmt; so folgt der (+)-gauche-Konformation selten eine weitere (+)-gauche-Konformation (genauso bei (−)-gauche), weil dies die Wahrscheinlichkeit einer Atomkollision erhöht. Die Diederwinkel der Aminosäureseitenketten (χ¹ und χ²) können in einem Janin-Plot abgebildet werden.

Siehe auch

Tetraederwinkel

Basierend auf einem Artikel in:

Wikipedia.de