Färbung (Graphentheorie)

Eine Färbung eines ungerichteten Graphen ordnet jedem Knoten bzw. jeder Kante im Graphen eine Farbe zu.

In der Graphentheorie beschäftigt man sich meist nur mit sogenannten „zulässigen“ oder „gültigen“ Färbungen (siehe unten), und versucht, Algorithmen zu entwickeln, die für einen vorgegebenen Graphen eine gültige Färbung mit möglichst wenigen Farben finden. Probleme aus der diskreten Mathematik, aber auch außermathematische Fragestellungen lassen sich manchmal in ein Färbungsproblem übersetzen, daher ist die Existenz oder Nichtexistenz solcher Algorithmen auch außerhalb der Graphentheorie von Interesse.

Knotenfärbungen

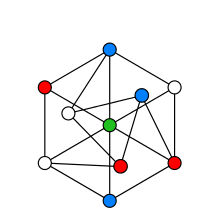
Eine gültige 4-Knotenfärbung eines Graphen. Mathematisch werden die unterschiedlichen Farben durch verschiedene natürliche Zahlen dargestellt

Ist G=(V,E) ein ungerichteter Graph ohne Mehrfachkanten und $f\colon V \rightarrow C \subseteq \mathbb{N}_0$ eine Abbildung der Knotenmenge in die Menge der natürlichen Zahlen, so nennt man eine Knotenfärbung von . Die Elemente aus werden die Farben genannt (Teils werden auch Abbildungen in beliebige abzählbare Mengen und nicht in die natürlichen Zahlen betrachtet. Dies ist aber nicht wichtig, notwendig ist bloß die Unterscheidbarkeit der Farben). Man nennt gültig oder zulässig, falls je zwei beliebige benachbarte Knoten nicht dieselbe Farbe besitzen:

$\forall v \in V: \forall w \in \Gamma (v): f(v)\ne f(w)\,,$

wobei $\Gamma(v)$ die Menge der Nachbarn von bezeichnet.

In diesem Fall heißt k-knotenfärbbar, falls es eine gültige Knotenfärbung von gibt, so dass nur Farben verwendet werden, also $\left|C\right|=k$ .

Eine zulässige Knotenfärbung eines Graphen ist eine Partition seiner Knotenmenge in unabhängige Mengen (eine Teilmenge der Knotenmenge eines Graphen heißt unabhängig, falls sie keine zwei benachbarten Knoten enthält).

Bei einer vollständigen Knotenfärbung existiert für jedes Paar $\{i,j\}$ von Farben eine Kante $\{x,y\}\in E(G)$ , sodass mit und mit gefärbt ist. Das heißt für jedes Farbenpaar existieren benachbarte Knoten, die mit diesen Farben gefärbt sind.

Anzahl der Färbungen

Wenn ein Graph färbbar ist, gibt es eine kleinste Zahl , sodass der Graph -knotenfärbbar ist. Diese Zahl wird die chromatische Zahl oder Knotenfärbungszahl des Graphen genannt und meist mit $\chi$ (G) bezeichnet. Existiert für noch so viele Farben keine Färbung setzt man symbolisch $\chi(G)=\infty$ .

Das chromatische Polynom eines Graphen gibt für jede Zahl die Anzahl der zulässigen -Färbungen an.

Bandbreite

Ist (V,E) ein einfacher Graph mit Knoten und $f \colon V \to\{1,\ldots,n\}$ eine eineindeutige Färbung der Knoten, dann bezeichnet

$\max_{\{x,y\}\in E} |f(x)-f(y)|$

die Bandbreite (englisch bandwidth) des Graphen bezüglich und

$\min_f \max_{\{x,y\}\in E} |f(x)-f(y)|$

die Bandbreite des Graphen. Die Ermittlung der Bandbreite ist eines der wenigen graphentheoretischen Probleme, das auch für Bäume NP-vollständig ist.

Eigenschaften

Jeder -partite Graph ist -knotenfärbbar, die Partitionsklassen entsprechen hier genau den Farben. Insbesondere sind alle bipartiten Graphen 2-färbbar. Jeder 2-färbbare Graph ist jedoch auch bipartit. Da man einen Graph in polynomieller Zeit auf Bipartitheit testen kann, ist demnach auch das 2-Färbbarkeitsproblem in polynomieller Zeit lösbar.
Ist ein Graph mit Kanten, so gilt $\chi (G) \leq \frac{1}{2} + \sqrt{2m+ \frac{1}{4}}$ .
Ein Greedy-Algorithmus liefert als obere Schranke für die chromatische Zahl eines Graphen den Maximalgrad des Graphen plus 1. Beispiele, die zeigen, dass diese Abschätzung bestmöglich ist, sind Kreise ungerader Länge und vollständige Graphen. Der -->Satz von Brooks zeigt, dass dies auch die einzigen Beispiele sind: Für jeden zusammenhängenden Graphen, der weder vollständig noch ein Kreis ungerader Länge ist, ist seine chromatische Zahl stets kleiner oder gleich dem Maximalgrad des Graphen.

Knotenfärbungen planarer Graphen

Darstellung einer kartographischen Färbung als Graph. Jedem Land wird ein Knoten zugewiesen, die Knoten werden durch Kanten verbunden genau dann wenn die beiden Länder benachbart sind.

Eines der klassischen Probleme der Graphentheorie ist die Frage, wie viele Farben man maximal braucht, um eine Landkarte so zu färben, dass je zwei aneinandergrenzende Länder nicht dieselbe Farbe haben. Dieses Problem lässt sich leicht in ein Knotenfärbungsproblem überführen (vgl. Bild rechts). Die graphentheoretisch äquivalente Frage lautet also: Was ist die chromatische Zahl eines planaren Graphen? Der Vier-Farben-Satz besagt, dass die chromatische Zahl eines planaren Graphen höchstens 4 ist. Enthält der Graph kein Dreieck, so ist er sogar 3-Knoten-färbbar. Trotzdem ist auch für planare Graphen das Bestimmen der chromatischen Zahl NP-schwer.

Algorithmen

Die Bestimmung der chromatischen Zahl eines Graphen ist NP-schwer, das heißt, dass es – aus Sicht der Komplexitätstheorie – vermutlich keinen Algorithmus gibt, der dieses Problem effizient löst. Die Bestimmung der chromatischen Zahl ist auch eines der Probleme von Karps 21 NP-vollständigen Problemen und damit eines der ersten Probleme, für die die NP-vollständigkeit gezeigt wurde. Ausnahmen sind bipartite Graphen (Das Entscheidungsproblem, ob ein gegebener Graph bipartit ist, besitzt lineare Zeitkomplexität, und ist zum Beispiel mit Tiefensuche lösbar) und perfekte Graphen (bei perfekten Graphen existieren Polynomialzeitalgorithmen zur Berechnung der chromatischen Zahl).

Das Knotenfärbungsproblem ist NP-vollständig.

Der zurzeit praktisch beste Algorithmus zur Bestimmung einer Knotenfärbung beruht auf einem Spalten-Generierungs-Ansatz (siehe Literatur). Weiterhin gibt es viele Färbungsheuristiken, die nach bestimmten Methoden gute Färbungen suchen und somit im Erfolgsfall eine obere Schranke für die chromatische Zahl liefern.

Anwendungen

Stundenplanprobleme lassen sich als Graphfärbungsprobleme formulieren: Die Knoten des Graphen sind dabei die zu platzierenden Veranstaltungen, und eine Kante wird zwischen zwei Veranstaltungen eingefügt, die nicht gleichzeitig stattfinden können. In der Schule wären das z.B. Stunden, die von demselben Lehrer unterrichtet werden sowie Stunden in derselben Klasse. Die möglichen Farben entsprechen den zuteilbaren Zeitfenstern.

Der Rot-Schwarz-Baum wird durch Knotenfärbung balanciert.

In gleicher Weise können beispielsweise Register-Zuweisungsprobleme in Prozessoren, Bandbreiten-Zuweisungsprobleme und auch viele Probleme aus der Mathematik als Graphenfärbungsprobleme formuliert werden.

Verallgemeinerungen

Eine Verallgemeinerung der Knotenfärbung ist der Begriff der Listenfärbung. Hierbei wird jedem Knoten eine „Liste“ von verfügbaren Farben zugeteilt und der Graph soll nun eine gültige Färbung aus diesen Listen erhalten. Des Weiteren gibt es die Totalfärbung, bei der sowohl Knoten als auch Kanten gefärbt werden sollen.

Basierend auf einem Artikel in:

Wikipedia.de