Baum (Graphentheorie)

Ein Baum ist in der Graphentheorie ein spezieller Typ von Graph, der zusammenhängend ist und keine geschlossenen Pfade enthält, d.h. damit lässt sich eine Monohierarchie modellieren. Je nachdem, ob die Kanten des Baums eine ausgezeichnete (und einheitliche) Richtung besitzen, lassen sich graphentheoretische Bäume unterteilen in ungerichtete Bäume und gewurzelte Bäume, und für gewurzelte Bäume in Out-Trees, bei denen die Kanten von der Wurzel ausgehen, und In-Trees, bei denen Kanten in Richtung Wurzel zeigen.

Darstellung aller Bäume^{[Anm.
1]} mit einer, zwei oder drei Kanten bei der ersten mathematischen Modellierung von Bäumen durch Arthur Cayley (1857)

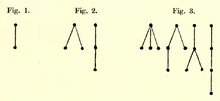
Durch Entfernen einer Kante zerfällt ein Baum in zwei Teilbäume und bildet damit einen so genannten Wald.

Definitionen

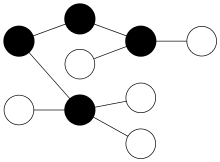
Ungerichteter Baum mit vier inneren Knoten (schwarz) und fünf Blättern (weiß)

Ein (ungerichteter) Baum ist ein zusammenhängender kreisfreier ungerichteter Graph. Die Knoten mit Grad 1 heißen Blätter die übrigen Knoten heißen innere Knoten.

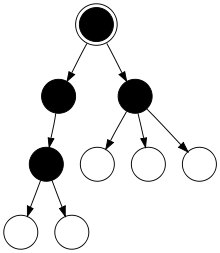
Gewurzelter Baum (hier: Out-Tree) mit einer Wurzel (umrandet), vier inneren Knoten (schwarz) und fünf Blättern (weiß)

Ein gerichteter Baum ist ein gerichteter Graph, der ein (ungerichteter) Baum ist, wenn man die Richtungen der Kanten ignoriert. Er ist also ein gerichteter schwach zusammenhängender kreisfreier Graph. Bei vielen Autoren müssen die Richtungen einheitlich von einem Knoten weg oder auf einen Knoten zu orientiert sein. Dafür gibt es aber auch den (schärferen) Begriff des gewurzelten Baums.

Ein gewurzelter Baum ist ein gerichteter von einem Knoten aus stark zusammenhängender kreisfreier Graph. Der den starken Zusammenhang definierende Knoten wird Wurzel genannt. Er hat Eingangsgrad 0 und ist der einzige Knoten mit dieser Eigenschaft. Alle Knoten mit Ausgangsgrad 0 heißen Blätter. Alle Knoten mit positivem Ausgangsgrad heißen innere Knoten. So geht die Definition eines Out-Trees.

Werden die Richtungen aller Kanten eines solchen Graphen invertiert, so wird er zu einem In-Tree. Dieser wird ebenfalls als gewurzelter Baum angesehen.

Man kann jeden ungerichteten Baum an einem beliebigen Knoten fassen und schütteln – die Schwerkraft gibt allen Kanten eine definierte Richtung von weg, die aus dem ursprünglich ungerichteten Baum einen gewurzelten macht mit als Wurzel.

Den m Kanten eines ungerichteten Baums kann man 2^m verschiedene Richtungen geben und so 2^m gerichtete Bäume ableiten. Genau n=m+1 davon sind Out-Trees und ebenso viele sind In-Trees. Entfernt man umgekehrt bei einem gerichteten Baum die Orientierung der Kanten, so erhält man einen (ungerichteten) Baum.

Spezielle Bäume

Es existiert eine Vielzahl von Begriffen, die Bäume näher spezifizieren. So gibt es zum Beispiel

leere Bäume (diese enthalten keine Knoten und Kanten),
Binärbäume,
Binomialbäume,
balancierte Bäume und
vollständige Binärbäume.

Äquivalente Charakterisierungen von Bäumen

Ein endlicher Graph G=(V,E) mit |V|=n Knoten und |E|=m Kanten kann durch folgende äquivalente Aussagen als Baum definiert werden:

Zwischen je zwei Knoten von gibt es genau einen Pfad.
ist zusammenhängend und enthält keinen Kreis
ist leer oder ist zusammenhängend und es gilt . (Es gibt immer eine Kante weniger als Knoten.)
ist leer oder enthält keinen Kreis und es gilt .
ist minimal zusammenhängend, das heißt ist zusammenhängend, aber nicht mehr zusammenhängend, sobald man eine beliebige Kante daraus entfernt.
ist maximal azyklisch, das heißt ist kreisfrei, aber jede weitere Kante zwischen zwei beliebigen Knoten erzeugt einen Kreis.

Im Falle unendlicher Graphen müssen hier die dritte und vierte Bedingung aus der Äquivalenz ausgenommen werden.

Zeichnen von Bäumen

Die grafische Ausgabe eines Baums ist ein nicht triviales Problem. Allgemein gilt, dass jeder Baum planar, das heißt ohne Überschneidungen der Kanten gezeichnet werden kann. Je nach Anwendungszweck gibt es weitere Wünsche an die Art der Ausgabe:

alle Kanten sind gerade Linien
alle Knoten haben ganzzahlige Koordinaten
möglichst kleiner Platzbedarf bei möglichst ästhetischem Ergebnis
alle Kanten vom Elternelement zum Kind streng monoton fallend

Es gibt verschiedene Algorithmen, deren Ergebnisse recht verschieden aussehen. Meist lösen sie nur einige, aber nicht alle Wünsche an die Ausgabe. Bekannte Algorithmen sind die HV-Bäume (Horizontal-Vertikal) und der Algorithmus von Walker.

Kombinatorik

Es gibt $n^{n-2}$ verschiedene bezeichnete Bäume mit Knoten. Diese Aussage ist als Cayley-Formel bekannt. Einen einfachen Beweis liefert der Prüfer-Code, der eine Bijektion zwischen allen möglichen Codes der Länge n-2 und allen bezeichneten Bäumen auf Knoten ermöglicht.

Wenn die Knoten nicht nummeriert sind, isomorphe Bäume (siehe Isomorphie von Graphen) also nicht mitgezählt werden, verhält sich diese Anzahl asymptotisch wie $C\cdot \alpha ^{n}\cdot n^{-{\tfrac {5}{2}}}$ mit $C\approx 0,534949606$ und $\alpha \approx 2,95576528565$ , wie Richard Otter im Jahr 1948 bewies. Eine genaue mathematische Formel ist nicht bekannt.

Die folgende Tabelle zeigt die mit Hilfe eines Computers bestimmten Anzahlen für $n\leq 12$ :

Anzahl der Bäume
n	mit nummerierten Knoten	ohne nummerierte Knoten
1	1	1
2	1	1
3	3	1
4	16	2
5	125	3
6	1.296	6
7	16.807	11
8	262.144	23
9	4.782.969	47
10	100.000.000	106
11	2.357.947.691	235
12	61.917.364.224	551

Spannbäume

→ Hauptartikel: Spannbaum

Jeder ungerichtete, zusammenhängende Graph enthält einen ihn aufspannenden Baum als Teilgraphen. Minimale Spannbäume haben eine möglichst kleine Anzahl von Kanten oder eine möglichst kleine Summe der Kantengewichte. Die Berechnung minimaler Spannbäume findet direkte Anwendung in der Praxis, beispielsweise für die Erstellung von kostengünstigen zusammenhängenden Netzwerken, wie beispielsweise Telefonnetzen oder elektrischen Netzen.

Verallgemeinerungen

Wald

→ Hauptartikel: Wald (Graphentheorie)

Ein Wald ist ein ungerichteter Graph, dessen Zusammenhangskomponenten Bäume sind.

k-Baum

Ein ungerichteter Graph heißt -Baum, wenn er wie folgt rekursiv erzeugbar ist:

Der vollständige Graph $K_{k}$ ist ein -Baum.
Fügt man zu einem -Baum einen neuen Knoten hinzu, indem man mit allen Knoten einer Clique der Größe aus verbindet, so ist dieser neue Graph ebenfalls ein -Baum.

Ein partieller -Baum entsteht durch die Entfernung von Kanten aus einem -Baum: Ist G = (V, E) ein -Baum, so ist H=(V,F) mit $F \subseteq E$ ein partieller -Baum.

Durch die angegebene Definition haben partielle k-Bäume immer mindestens k Knoten, was nicht immer wünschenswert ist. Darum gibt es auch die folgende Definition:

Ein partieller k-Baum ist ein Teilgraph eines k-Baumes.

Eine weitere Eigenschaft ist, dass die Menge der partiellen k-Bäume gleich der Menge der Graphen mit Baumweite höchstens k ist.

Siehe auch

Anmerkungen

↑ Einige der dargestellten Bäume sind isomorph zueinander; nämlich beide Bäume in Fig. 2 sowie in Fig. 3 (von links gezählt) die Bäume 1 und 3 sowie 2 und 4.

Basierend auf einem Artikel in:

Wikipedia.de