Website durchsuchen

Clique (Graphentheorie)


Eine Clique bezeichnet in der Graphentheorie eine Teilmenge von Knoten in einem ungerichteten Graphen, bei der jedes Knotenpaar durch eine Kante verbunden ist. Zu entscheiden, ob ein Graph eine Clique einer bestimmten Mindestgröße enthält, wird Cliquenproblem genannt und gilt, wie das Finden von größten Cliquen, als algorithmisch schwierig (NP-vollständig).

Definitionen

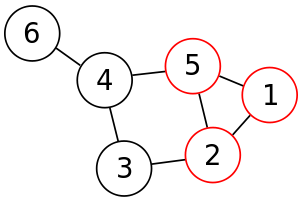
Ein Graph mit einer Clique der Größe 3.

Sei G=(V,E) ein ungerichteter Graph ohne Mehrfachkanten und U eine Teilmenge von V. Eine Clique ist eine Teilmenge U von V, die einen vollständigen Teilgraphen induziert. Ist U eine Clique, so gilt also für den Teilgraph {\displaystyle H=(U,F)}, wobei F alle Kanten aus E enthält, die zwei Knoten in U verbinden, dass je zwei beliebige verschiedene Knoten v und w aus U durch eine Kante miteinander verbunden sind.

Eine Clique U von G nennt man maximal, wenn man keinen weiteren Knoten v aus V zu U hinzufügen kann, so dass U zusammen mit v eine Clique ist. Gibt es in G keine Clique, die mehr Elemente als U enthält, so nennt man U größte Clique. Die Anzahl der Elemente einer größten Clique nennt man Cliquenzahl.

Als Cliquenüberdeckung von G der Größe k bezeichnet man eine Partition der Knotenmenge V(G) in k paarweise disjunkte Cliquen {\displaystyle V_{1},V_{2},\ldots ,V_{k}}. Aus den Cliquen eines Graphen ergibt sich dessen Cliquen-Graph.

Gerichtete Graphen oder solche mit Mehrfachkanten sind nicht Gegenstand derartiger Betrachtungen, da es nicht auf die Richtung oder Vielfachheit der Kanten ankommt.

Eigenschaften

Zu jeder Clique eines Graphen gibt es eine stabile Menge im Komplementgraphen.

Probleme und Komplexität

Das Entscheidungsproblem zu einem Graphen G und einer natürlichen Zahl k zu entscheiden, ob G eine Clique der Größe mindestens k enthält, wird Cliquenproblem (CLIQUE) genannt. Das zugehörige Optimierungsproblem fragt nach der Cliquenzahl eines Graphen. Das zugehörige Suchproblem fragt nach einer größten Clique. Diese drei Probleme sind polynomiell äquivalent.

Das Cliquenproblem ist eines von Karps 21 NP-vollständigen Problemen. Die zugehörigen Optimierungs- und Suchprobleme sind NP-äquivalent. Für den Nachweis der NP-Schwere des Cliquenproblems existiert eine Reduktion von 3-SAT auf das Cliquenproblem.

Eine größte Clique lässt sich jedoch in polynomieller Zeit berechnen, wenn der Komplementgraph bipartit ist. Tatsächlich gilt sogar etwas stärker, dass die Cliquenzahl in perfekten Graphen in polynomieller Zeit berechnet werden kann. Da die chromatische Zahl und die Cliquenzahl in solchen Graphen identisch sind, ist auch ihre chromatische Zahl in polynomieller Zeit berechenbar. Die Berechnung einer maximalen Clique gelingt bereits mit einem einfachen Greedy-Algorithmus.

Software

Algorithmen zum Finden und Manipulieren von Cliquen sind in der freien Python-Bibliothek NetworkX implementiert.

Trenner
Basierend auf einem Artikel in: Extern Wikipedia.de
Seitenende
Seite zurück
©  biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.11. 2020