
Umfang (Geometrie)
Umfang
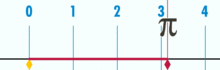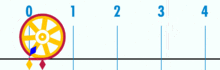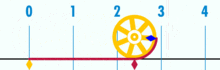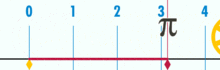
des Kreises:
U = d·π (hier ist d = 1)
U = d·π (hier ist d = 1)
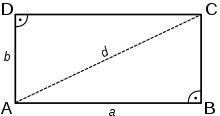
Umfang des Rechtecks:
U = 2·a + 2·b = 2·(a + b)
U = 2·a + 2·b = 2·(a + b)
Der Umfang einer ebenen Figur, die durch eine Linie begrenzt ist, bezeichnet die Länge ihrer Begrenzungslinie.
Die Formel für den Kreisumfang lautet:
steht dabei für den Umfang,
für den Radius des Kreises,
für die Kreiszahl mit dem Wert 3,14159265… und
für den Kreisdurchmesser.
Der Umfang eines Vielecks ist die Summe seiner Seitenlängen.

Herzkurve
![{\displaystyle \gamma \colon [0,2\pi ]\rightarrow \mathbb {R} ^{2}}](/svg/63900262a960d64137e54e681e881ab7ae9d2b7d.svg)
(Zeichnung mit )
)



(Zeichnung mit
Wird die Begrenzungslinie der Figur durch eine geschlossene stückweise glatte
Parameterkurve
beschrieben mit
,
so lässt sich der Umfang
über das folgende Integral
berechnen:
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.01. 2022