Zyklische Gruppe
In der Gruppentheorie
ist eine zyklische Gruppe eine Gruppe,
die von einem einzelnen Element
erzeugt
wird. Sie besteht nur aus Potenzen des Erzeugers
:
Eine Gruppe
ist also zyklisch, wenn sie ein Element
enthält, sodass jedes Element von
eine Potenz von
ist. Gleichbedeutend damit ist, dass es ein Element
gibt, sodass
selbst die einzige Untergruppe
von
ist, die
enthält. In diesem Fall wird
ein erzeugendes Element oder kurz ein Erzeuger von
genannt.
Zyklische Gruppen sind die einfachsten Gruppen und können vollständig
klassifiziert werden: Für jede natürliche
Zahl
(für diese Aussage betrachten wir 0 nicht als natürliche Zahl) gibt es eine
zyklische Gruppe
mit genau
Elementen, und es gibt die unendliche zyklische Gruppe, die additive Gruppe der
ganzen
Zahlen
.
Jede andere zyklische Gruppe ist zu einer dieser Gruppen isomorph.
Veranschaulichung
Drehgruppen
Die endlichen zyklischen Gruppen können veranschaulicht werden als
Drehgruppen regulärer Vielecke
in der Ebene. Zum Beispiel besteht die Gruppe
aus den möglichen Drehungen der Ebene, die ein vorgegebenes Quadrat in sich
überführen.
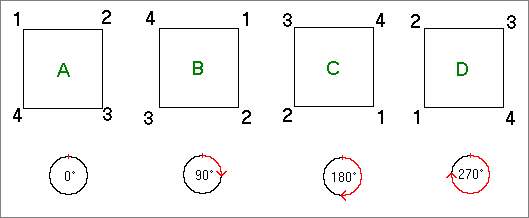
Die obenstehende Abbildung zeigt ein Quadrat A und die Stellungen B, C und D,
in die es durch Drehen überführt werden kann. Darunter ist jeweils die dazu
nötige Drehung angegeben. Die Elemente der zyklischen Gruppe sind hier die
Bewegungen und nicht die Stellungen des Quadrats. Das heißt, die Gruppe
besteht in dieser Darstellung aus der Menge {0°, 90°, 180°, 270°}. Die
Verknüpfung der Elemente ist die Hintereinanderausführung der Drehungen; das
entspricht einer Addition der Winkel. Dabei stimmt die Drehung um 360° mit der
Drehung um 0° überein, die Winkel werden also genau genommen modulo 360°
addiert.
Lässt man nicht nur Drehungen der Ebene zu, sondern auch Spiegelungen, dann erhält man im Fall von Vielecken die so genannten Diedergruppen.
Beachte auch, dass die Drehgruppe des Kreises, ,
nicht zyklisch ist.
Restklassengruppen
Eine andere Darstellung einer zyklischen Gruppe liefert die Addition modulo
einer Zahl, die so genannte Restklassenarithmetik.
In der additiven Gruppe
ist die Restklasse der 1 ein Erzeuger, das heißt, man kann jede andere
Restklasse erhalten, indem man die 1 wiederholt mit sich selbst addiert. Am
Beispiel
bedeutet dies, dass sich alle 4 Elemente als Summe von 1 darstellen lassen, also
1 = 1, 2 = 1+1, 3 = 1+1+1, 0 = 1+1+1+1. Die Restklassengruppe
verhält sich genauso wie die oben beschriebene Drehgruppe {0°, 90°, 180°, 270°}:
0 entspricht 0°, 1 entspricht 90° usw: Diese beiden Gruppen sind isomorph.
Schreibweisen
Für endliche zyklische Gruppen gibt es im Wesentlichen drei Schreibweisen:
,
und
.
Für nichtendliche zyklische Gruppen stehen die beiden Schreibweisen
und
zur Verfügung. Als Gruppenoperation wird in
meist die Multiplikation und in
,
und
die Addition verwendet.
Die Schreibweisen ,
und
rühren daher, dass die additiven Gruppen der Restklassenringe
und von
selbst die bekanntesten Vertreter zyklischer Gruppen sind. Im Gegensatz zur
-Schreibweise
verleiten sie jedoch dazu, das Vorhandensein einer Ringstruktur anzunehmen.
Die Bezeichnung
wird zudem auch noch im Zusammenhang mit p-adischen Zahlen
verwendet.
Eigenschaften
Alle zyklischen Gruppen sind abelsche Gruppen.
Eine zyklische Gruppe kann mehrere Erzeuger haben. Die Erzeuger von
sind +1 und -1, die Erzeuger von
sind die Restklassen, die teilerfremd
zu
sind; ihre Anzahl
wird von der Eulerschen
φ-Funktion angegeben.
Ist allgemein
ein Teiler von
,
dann ist
die Anzahl der Elemente von
,
die die Ordnung
haben:
.
Das direkte
Produkt zweier zyklischer Gruppen
und
ist genau dann zyklisch, wenn
und
teilerfremd
sind; in diesem Fall ist das Produkt isomorph zu
.
Jede endlich erzeugte abelsche Gruppe ist direktes Produkt endlich vieler endlicher und unendlicher zyklischer Gruppen.
Der Gruppenexponent
einer endlichen zyklischen Gruppe ist gleich ihrer Ordnung. Jede
endliche zyklische Gruppe ist isomorph
zur additiven Gruppe des Restklassenring
,
der Isomorphismus ist dabei der diskrete
Logarithmus: Ist
ein Erzeuger von
,
dann ist die Abbildung
ein Isomorphismus.
Untergruppen und Faktorgruppen
Alle Untergruppen und Faktorgruppen von
zyklischen Gruppen sind zyklisch. Insbesondere sind die Untergruppen von
von der Form
mit einer natürlichen Zahl
zyklisch. Alle diese Untergruppen sind verschieden, und für
sind sie isomorph zu
.
Der Verband
der Untergruppen von
ist isomorph zum dualen Verband der natürlichen Zahlen mit der Teilbarkeit. Alle
Faktorgruppen von
sind endlich, mit Ausnahme der trivialen Faktorgruppe
.
Für jeden positiven Teiler
von
hat die Gruppe
genau eine Untergruppe der Ordnung
,
nämlich die von dem Element
erzeugte Untergruppe
.
Andere als diese Untergruppen gibt es nicht. Der Untergruppenverband ist deshalb
isomorph zum Teilerverband von
.
Eine zyklische Gruppe ist genau dann einfach, wenn ihre Ordnung eine Primzahl ist.
Endomorphismen und Automorphismen
Der Endomorphismenring (siehe Gruppenhomomorphismus)
der Gruppe
ist Ring-isomorph zum Restklassenring
.
Unter diesem Isomorphismus entspricht die Restklasse
von
dem Endomorphismus
von
,
der jedes Element auf seine
-te
Potenz abbildet. Daraus folgt, dass die Automorphismengruppe
von
isomorph zur Gruppe
,
der Einheitengruppe
des Rings
,
ist. Diese Gruppe besteht aus den Elementen, die teilerfremd zu
sind, und hat somit genau
Elemente.
Der Endomorphismenring der zyklischen Gruppe
ist isomorph zum Ring
,
und die Automorphismengruppe ist isomorph zur Einheitengruppe
von
,
und diese ist isomorph zur zyklischen
Gruppe
.
Algebraische Eigenschaften
Ist
eine natürliche Zahl, dann ist
genau dann zyklisch, wenn
gleich 2, 4,
oder
ist, für eine Primzahl
und eine natürliche Zahl
.
Die Erzeuger dieser zyklischen Gruppe heißen Primitivwurzeln
modulo
.
Insbesondere ist für jede Primzahl
die Gruppe
zyklisch mit
-1
Elementen. Allgemeiner ist jede endliche Untergruppe der multiplikativen
Gruppe eines Körpers
zyklisch.
Die Galoisgruppe einer
endlichen Körpererweiterung
eines endlichen
Körpers ist eine endliche zyklische Gruppe. Umgekehrt gibt es für jeden
endlichen Körper
und jede endliche zyklische Gruppe
eine endliche Körpererweiterung
mit Galoisgruppe
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.02. 2021