Galoisgruppe
Die Galoisgruppe (nach Évariste Galois) ist eine Gruppe, mit deren Hilfe Körpererweiterungen in der Algebra untersucht werden können.
Die Zwischenkörper einer Körpererweiterung lassen sich gewissen Untergruppen der Galoisgruppe zuordnen. Damit kann man Strukturuntersuchungen von Körpererweiterungen mit gruppentheoretischen Untersuchungen in Verbindung bringen. Da zu endlichdimensionalen Körpererweiterungen endliche Galoisgruppen gehören, können damit solche Strukturuntersuchungen oft stark vereinfacht werden.
Historisch bedeutsam war, dass die klassischen Fragen der Konstruierbarkeit – mit Zirkel und Lineal – gewisser algebraischer Zahlen damit in eine gruppentheoretische Formulierung übersetzt werden konnten. Einzelheiten zur klassischen Fragestellung der Konstruierbarkeit mit Zirkel und Lineal, Beispiele und deren moderne Lösung siehe unter → Konstruierbares Polygon.
Definition
Sei
(lies: „
über
“)
eine Körpererweiterung. Das heißt:
und
sind Körper
und der Körper
ist als Unterring in
enthalten. Damit ist
zugleich ein (nicht notwendig endlichdimensionaler)
-Vektorraum.
In dieser Situation heißt die Gruppe aller Körperautomorphismen des
Erweiterungskörpers ,
die den Grundkörper
elementweise festlassen, die Galoisgruppe von
über
und wird mit
bezeichnet, formal
.
Dies kann auch so formuliert werden: Die Galoisgruppe von
über
besteht genau aus den Körperautomorphismen von
,
die zugleich Vektorraumendomorphismen
von
als
-Vektorraum
sind.
Galoisgruppe eines Polynoms
Sei
ein Körper. Als Galoisgruppe des Polynoms
im Polynomring
wird die Gruppe
bezeichnet, wobei
ein Zerfällungskörper
des Polynoms
ist. Man spricht in diesem Fall auch von dem Zerfällungskörper, da
Zerfällungskörper – und damit die Galoisgruppe eines Polynoms –
bis auf Isomorphie eindeutig bestimmt sind.
Der Zerfällungskörper
eines Polynoms ist normal über dem Grundkörper
.
In diesem Fall ist die – hier endlichdimensionale – Körpererweiterung
bereits dann galoissch, wenn die über
irreduziblen Faktoren von
separabel sind. Der Artikel Galoistheorie
behandelt den Begriff der Galoisgruppe eines Polynoms, für diesen Fall genügt
die unten genannte erste Fassung des Hauptsatzes – der Hauptsatz für endliche
Galoiserweiterungen.
Abweichende Bedeutungen des Begriffs
Besonders nützlich ist die Galoisgruppe, wenn die Körpererweiterung
eine Galoiserweiterung (s. u.) ist. In der Literatur wird oft nur in diesem
Falle von „Galoisgruppe“ gesprochen. Die in diesem Artikel verwendete Gruppe der
-Automorphismen
von
wird dann mit
bezeichnet.
Eigenschaften
- Die Galoisgruppe ist eine Untergruppe der Automorphismengruppe
von
.
- Ist die Körpererweiterung
endlich, d.h. ist
endlichdimensional über
, so ist die Gruppenordnung von
kleiner gleich dem Erweiterungsgrad
. In diesem Fall existiert für jedes Körperelement
das Minimalpolynom
von
über
. Ist
eine endliche Galoiserweiterung, dann gilt
.
- Sei
ein Zerfällungskörper des Polynoms
über
. Jeder Automorphismus aus der Galoisgruppe
des Polynoms
bildet eine Nullstelle von
wieder auf eine Nullstelle ab. Die Galoisgruppe operiert also auf der Menge der Nullstellen von
im Körper
,
als Permutationsgruppe und ist damit isomorph zu einer Untergruppe der symmetrischen Gruppe
. Für ein separables, über
irreduzibles Polynom
ist diese Operation sogar transitiv, das heißt zu zwei verschiedenen Nullstellen
gibt es ein Element
der Galoisgruppe, das
auf
abbildet:
.
Galoiskorrespondenz, Abgeschlossene Untergruppen und Zwischenkörper
Man kann jedem Zwischenkörper
der Erweiterung
die Untergruppe der Galoisgruppe
zuordnen, deren Elemente
elementweise fest lässt, und umgekehrt jeder Untergruppe
von
den Zwischenkörper, den sie fixiert. Nach Hungerford (1981) wird hier für beide
Zuordnungen, die beide auch als Galoiskorrespondenz bezeichnet werden,
die „Priming-Notation“ verwendet:
Für Zwischenkörper
und
der Erweiterung, Untergruppen
und
von
gelten folgende Beziehungen:
und
,
,
,
,
und
,
und
.
Die Körpererweiterung
heißt hier Galoiserweiterung, wenn sie normal und separabel ist. Dies ist
genau dann der Fall, wenn
gilt, wenn also die Galoisgruppe außer dem Grundkörper keine weiteren Elemente
von
fixiert. Da in allen Fällen
gilt, ist die Erweiterung genau dann galoissch, wenn
ist. Dieselbe Bedingung gilt für Zwischenkörper
:
Die Erweiterung
ist genau dann eine Galoiserweiterung, wenn
gilt. Die Begriffe normal und separabel werden im Artikel Körpererweiterung
unabhängig von den hier verwendeten Zuordnungen definiert. Dort wird im
Abschnitt Galoiserweiterung
dieselbe für den Fall definiert, dass die Erweiterung algebraisch ist. Die hier
verwendete Definition lässt nach Emil Artin und Hungerford (1981) auch nicht algebraische Erweiterungen zu.
Abgeschlossenheit
Nach Hungerford (1981) heißt eine Untergruppe
der Galoisgruppe oder ein Zwischenkörper
der Erweiterung abgeschlossen, wenn
gilt.
- Alle Objekte
, die als Bilder der oben beschriebenen Korrespondenzen auftreten, sind abgeschlossen (nach 6.).
- Die triviale Untergruppe 1,
und
sind abgeschlossen.
- Die Erweiterung
ist genau dann eine Galoiserweiterung, wenn
abgeschlossen ist.
Mit den am Anfang des Abschnitts vereinbarten Bezeichnungen gilt:
- Wenn
abgeschlossen ist und
endlich ist, dann ist
abgeschlossen und es gilt
.
- Wenn
abgeschlossen ist und
endlich ist, dann ist
abgeschlossen und
.
- Speziell gilt (für
): Jede endliche Untergruppe der Galoisgruppe ist abgeschlossen.
- Wenn
eine endlichdimensionale Galoiserweiterung von
ist, dann sind alle Zwischenkörper und alle Untergruppen der Galoisgruppe abgeschlossen und die Galoisgruppe hat die Ordnung
.
Hauptsätze der Galoistheorie
Endlichdimensionale Körpererweitung
Ist
eine endlichdimensionale Galoiserweiterung von
,
dann vermittelt die Galoiskorrespondenz eine Bijektion zwischen der Menge
der Zwischenkörper und der Menge der Untergruppen der Galoisgruppe. Diese
Korrespondenz bildet den Teilmengenverband der Zwischenkörper (mit der Ordnung
)
auf den Verband der Untergruppen (mit der Ordnung
)
ordnungstreu ab, wobei die Teilmengenbeziehung umgekehrt wird. Dabei gilt:
- Die relative Dimension von zwei Zwischenkörpern ist gleich dem relativen Index der korrespondierenden Untergruppen.
ist galoissch über jedem Zwischenkörper
. Die Galoisgruppe
stimmt mit der Untergruppe
überein.
- Ein Zwischenkörper
ist galoissch über
genau dann, wenn die korrespondierende Untergruppe
ein Normalteiler der Galoisgruppe
ist. In diesem Fall ist die Faktorgruppe
isomorph zur Galoisgruppe
des Körpers
über
.
Unendlichdimensionale algebraische Erweiterung
Ist
eine algebraische, nicht notwendig endlichdimensionale Galoiserweiterung von
,
dann vermittelt die Galoiskorrespondenz eine Bijektion zwischen der Menge
aller Zwischenkörper und der Menge der abgeschlossenen
Untergruppen der Galoisgruppe. Diese Korrespondenz bildet den Teilmengenverband
der Zwischenkörper (mit der Ordnung
)
auf den Verband der abgeschlossenen Untergruppen (mit der Ordnung
)
ordnungstreu ab, wobei die Teilmengenbeziehung umgekehrt wird. Dabei gilt:
ist galoissch über jedem Zwischenkörper
. Die Galoisgruppe
stimmt mit der Untergruppe
überein.
- Ein Zwischenkörper
ist galoissch über
genau dann, wenn die korrespondierende Untergruppe
ein Normalteiler der Galoisgruppe
ist. In diesem Fall ist die Faktorgruppe
isomorph zur Galoisgruppe
des Körpers
über
.
Beispiele
- Die komplexen
Zahlen sind ein Körper
und enthalten den Körper der reellen Zahlen. Also
ist
eine Körpererweiterung. Da
ein Vektorraum der Dimension 2 über
ist (
ist eine Basis), gilt
. Die Galoisgruppe enthält die Identität und die komplexe Konjugation. Die Wurzelmenge des Minimalpolynoms
ist
. Die Identität bildet diese beiden Elemente wieder auf sich selbst ab, während sie von der komplexen Konjugation permutiert werden. Also ist die Galoisgruppe eingeschränkt auf die Wurzelmenge isomorph zur symmetrischen Gruppe
- Sei
, der Körper der rationalen Funktionen
über K. Dann ist für jede Zahl
die durch
definierte Abbildung ein K-Automorphismus. Ist der Körper K unendlich, so gibt es unendlich viele dieser Automorphismen und die Galoisgruppe
ist eine unendliche Gruppe. Ist das Element
selbst keine Einheitswurzel, dann ist die von dem Automorphismus
erzeugte Untergruppe von G nicht abgeschlossen.
- Der Körper der reellen Zahlen lässt keine nichttrivialen Automorphismen
zu, denn seine Anordnung
ist eine algebraische Invariante: Es ist
für zwei reelle Zahlen genau dann, wenn
ein Quadrat ist. Daher ist der Körper der reellen Zahlen über keinem seiner echten Teilkörper galoissch, dasselbe gilt für den Körper der reellen algebraischen Zahlen.
- Allgemeiner trifft das auf alle euklidischen Körper zu: die Galoisgruppe eines euklidischen Körpers über einem seiner Teilkörper ist immer die triviale Gruppe.
Galoisgruppe eines kubischen Polynoms
Das folgende ausführliche Beispiel zeigt am Polynom ,
wie mit Hilfe der Galoisgruppe Zwischenkörper bestimmt werden können.
Der von der reellen Zahl
über
erzeugte Zahlkörper
hat die Galoisgruppe 1, da keine weiteren Nullstellen des Minimalpolynoms
von
im (reellen!) Zahlkörper
liegen. Diese Erweiterung ist also nicht galoissch. Ihr Grad ist 3, da
isomorph zu dem Faktorring
ist (siehe Faktorring).
Dasselbe gilt für die beiden Zahlkörper
und
,
die von den beiden nichtreellen Wurzeln
und
von
über
erzeugt werden. Alle drei Körper sind isomorphe Zwischenkörper des
Zerfällungskörpers
des Polynoms
.
Da der Grundkörper
als Körper mit der Charakteristik 0 perfekt ist, ist
der gesuchte Zerfällungskörper
eine Galoiserweiterung von
und die Galoisgruppe
muss transitiv auf den Nullstellen von
operieren. Die einzige echte Untergruppe der symmetrischen Gruppe
,
die transitiv auf
operiert, ist der von dem 3-Zyklus
erzeugte Normalteiler der
,
die alternierende
Gruppe
.
Da wir bereits drei echte Zwischenkörper identifiziert haben und die
keine echten Untergruppen hat, kann es sich noch nicht um die volle Galoisgruppe
handeln. Diese kann also nur die volle symmetrische Gruppe sein, es gilt also
.
Neben den Zwischenkörpern, die wir schon identifiziert haben, muss noch ein
normaler Zwischenkörper
vorhanden sein, der zweidimensional über
ist (Index von
).
Dieser bleibt fix unter zyklischen
Vertauschungen der Nullstellen, das trifft nur auf den Kreisteilungskörper
der dritten Einheitswurzeln zu, der durch die Einheitswurzel
erzeugt wird. Alle Ergebnisse werden in dem Diagramm unten gezeigt.
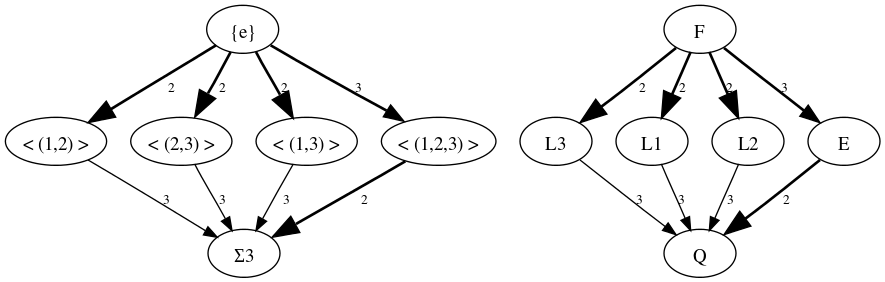
Die Zwischenkörper können nun unter anderem dazu verwendet werden, verschiedene Darstellungen des Zerfällungskörpers zu gewinnen:
, dies folgt – ganz ohne Galoistheorie – aus seiner Definition als Zerfällungskörper.
: Dass zwei Nullstellen zur Erzeugung genügen, folgt aus der Tatsache, dass zwischen den Körpern, die durch eine Nullstelle erzeugt werden und
keine weiteren Körper liegen.
: Hier wird die (in diesem Fall einzige maximale) Subnormalreihe der Galoisgruppe nachgebildet (in der Graphik der Pfad rechts außen). Die relativen Erweiterungen in /SPAN>
sind alle galoissch und ihre Galoisgruppen sind einfache abelsche Gruppen.
lässt sich auch als einfache Körpererweiterung darstellen:
ist sicher ein Element von
und wird von keinem nichttrivialen Element der Galoisgruppe fixiert. Daher ist
.
Natürlich können in allen genannten Darstellungen die Nullstellen
beliebig ausgetauscht werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.06. 2021