Permutation

Alle sechs Permutationen dreier farbiger Kugeln

Unter einer Permutation (von permutare ‚vertauschen‘) versteht man in der Kombinatorik eine Anordnung von Objekten in einer bestimmten Reihenfolge. Je nachdem, ob manche Objekte mehrfach auftreten dürfen oder nicht, spricht man von einer Permutation mit Wiederholung oder einer Permutation ohne Wiederholung. Die Anzahl der Permutationen ohne Wiederholung ergibt sich als Fakultät, während die Anzahl der Permutationen mit Wiederholung über Multinomialkoeffizienten angegeben wird.

In der Gruppentheorie ist eine Permutation ohne Wiederholung eine bijektive Selbstabbildung einer in der Regel endlichen Menge, wobei als Referenzmengen meist die ersten natürlichen Zahlen verwendet werden. Die Menge der Permutationen der ersten natürlichen Zahlen bildet mit der Hintereinanderausführung als Verknüpfung die symmetrische Gruppe vom Grad . Das neutrale Element dieser Gruppe stellt die identische Permutation dar, während das inverse Element die inverse Permutation ist. Die Untergruppen der symmetrischen Gruppe sind die Permutationsgruppen.

Wichtige Kenngrößen von Permutationen sind ihr Zykeltyp, ihre Ordnung und ihr Vorzeichen. Mit Hilfe der Fehlstände einer Permutation lässt sich auf der Menge der Permutationen fester Länge eine partielle Ordnung definieren. Über ihre Inversionstafel kann zudem jeder Permutation eine eindeutige Nummer in einem fakultätsbasierten Zahlensystem zugeordnet werden. Wichtige Klassen von Permutationen sind zyklische, fixpunktfreie, selbstinverse und alternierende Permutationen.

Permutationen besitzen vielfältige Einsatzbereiche innerhalb und außerhalb der Mathematik, beispielsweise in der linearen Algebra (Leibniz-Formel), der Analysis (Umordnung von Reihen), der Graphentheorie und Spieltheorie, der Kryptographie (Verschlüsselungsverfahren), der Informatik (Sortierverfahren) und der Quantenmechanik (Pauli-Prinzip).

Kombinatorische Grundlagen

Permutationen vier farbiger Kugeln ohne Wiederholung (links) und mit Wiederholung (mitte und rechts).

Problemstellung

Eine Permutation ist eine Anordnung von Objekten in einer bestimmten Reihenfolge oder eine Umordnung von Objekten aus einer vorgegebenen Reihung. Beispiele für Permutationen sind:

Ein Anagramm ist eine Permutation der Buchstaben eines Wortes, wie beispielsweise ENKEL und NELKE.
Das Mischen der Karten eines Kartenspiels ist (im Idealfall) eine zufällige Permutation der Karten.
Im Volleyball ist der Stellungswechsel nach Eroberung des Aufschlagsrechts eine zyklische Permutation der Spieler.
Viele Sortierverfahren arbeiten mit sukzessiven Transpositionen, also Permutationen, die genau zwei Objekte vertauschen.

Werden in einer solchen Anordnung nicht alle Objekte ausgewählt, spricht man statt von einer Permutation von einer Variation, spielt die Reihenfolge bei der Auswahl keine Rolle, von einer Kombination. In der abzählenden Kombinatorik stellt sich nun die Frage nach der Anzahl möglicher Permutationen. Hierbei unterscheidet man den Fall, dass alle Objekte verschieden sind, von dem Fall, dass manche der Objekte identisch sind.

Permutation ohne Wiederholung

Eine Permutation ohne Wiederholung ist eine Anordnung von Objekten, die alle unterscheidbar sind. Nachdem es für das erste Objekt Platzierungsmöglichkeiten gibt, kommen für das zweite Objekt nur noch n-1 Möglichkeiten in Betracht, für das dritte Objekt nur mehr n-2 und so weiter bis zum letzten Objekt, dem nur noch ein freier Platz bleibt. Die Anzahl der möglichen Permutationen von Objekten wird demnach durch die Fakultät

$n!=n\cdot (n-1)\cdot (n-2)\cdot \ldots \cdot 1$

angegeben.

Beispielsweise gibt es $4!=4\cdot 3\cdot 2\cdot 1=24$ mögliche Anordnungen von vier verschiedenfarbigen Kugeln in einer Reihe.

Permutation mit Wiederholung

Eine Permutation mit Wiederholung ist eine Anordnung von Objekten, von denen manche nicht unterscheidbar sind. Sind genau Objekte identisch, dann sind diese auf ihren Plätzen vertauschbar, ohne dass sich dabei eine neue Reihenfolge ergibt. Auf diese Weise sind genau Anordnungen gleich. Die Anzahl der Permutationen von Objekten, von denen identisch sind, ist demnach durch die fallende Faktorielle

${\frac {n!}{k!}}=n\cdot (n-1)\cdot \ldots \cdot (k+1)=n^{\underline {n-k}}$

gegeben. Gibt es nicht nur eine, sondern Gruppen mit jeweils $k_{1},\ldots ,k_{s}$ identischen Objekten, so können all diese Objekte auf ihren Plätzen vertauscht werden, ohne dass sich neue Anordnungen ergeben. Zählt man auch die Objekte, die nur einmal vorkommen, mit Vielfachheit , dann gilt $k_{1}+\ldots +k_{s}=n$ und die Anzahl der möglichen Permutationen wird durch den Multinomialkoeffizienten

${\frac {n!}{k_{1}!\cdot \ldots \cdot k_{s}!}}={\binom {n}{k_{1},\ldots ,k_{s}}}$

angeben.

Beispielsweise gibt es ${\tfrac {4!}{2!\,1!\,1!}}={\tfrac {24}{2}}=12$ mögliche Anordnungen von vier farbigen Kugeln in einer Reihe, wenn genau zwei der Kugeln die gleiche Farbe aufweisen, und ${\tfrac {4!}{2!\,2!}}={\tfrac {24}{4}}=6$ mögliche Anordnungen, wenn jeweils zwei Kugeln gleichfarbig sind.

Definition

Sei $X=\{x_{1},x_{2},\ldots ,x_{n}\}$ eine Menge mit Elementen, dann ist eine -stellige Permutation (ohne Wiederholung) eine bijektive Abbildung

$\pi \colon X\rightarrow X$ ,

die jedem Element der Menge ein Element der gleichen Menge zuordnet. Anschaulich nimmt durch die Permutation jedes Element $x_{i}$ für $i=1,\ldots ,n$ den Platz des ihm zugeordneten Elements $\pi (x_{i})$ ein. Aufgrund der Bijektivität der Abbildung werden dabei zwei verschiedene Elemente niemals auf das gleiche Element abgebildet. Der Fall n=0 ist ebenfalls zugelassen und ist dann die leere Menge.

Da auf jeder endlichen Menge eine lineare Ordnung festgelegt werden kann (beispielsweise die durch die Indizierung der Elemente gegebene), kann man sich bei der mathematischen Betrachtung von Permutationen stets auf die ersten natürlichen Zahlen als Referenzmenge beschränken. Eine Permutation ist dann eine bijektive Abbildung

$\pi \colon \{1,2,\ldots ,n\}\rightarrow \{1,2,\ldots ,n\}$ ,

die jeder natürlichen Zahl zwischen und genau eine Zahl im gleichen Bereich zuordnet. Stellt man sich alle Zahlen in einer Liste aneinandergereiht vor, dann nimmt die Zahl $j\in \{1,\ldots ,n\}$ durch die Permutation den Platz mit der Nummer $\pi (j)$ ein.

Notation

Zweizeilenform

In der ausführlichen Darstellung einer -stelligen Permutation $\pi$ schreibt man diese als Matrix mit zwei Zeilen und Spalten. In der oberen Zeile stehen die Zahlen von bis (in beliebiger Reihenfolge). Unter jeder Zahl $j\in \{1,\ldots ,n\}$ steht dann in der zweiten Zeile der Funktionswert $\pi (j)$ :

$\pi ={\begin{pmatrix}1&2&\cdots &n\\\pi \left(1\right)&\pi \left(2\right)&\cdots &\pi \left(n\right)\end{pmatrix}}$

Auch in der zweiten Zeile steht somit jede Zahl von bis genau einmal.

Beispiel

Die Permutation $\pi \colon \{1,2,3,4\}\rightarrow \{1,2,3,4\}$ mit $\pi (1)=2,\pi (2)=4,\pi (3)=3$ und $\pi (4)=1$ wird in der Zweizeilenform durch

$\pi ={\begin{pmatrix}1&2&3&4\\2&4&3&1\end{pmatrix}}$

notiert.

Tupelschreibweise

Bei der kompakteren Tupelschreibweise schreibt man lediglich die Funktionswerte $\pi (j)$ in eine Zeile:

$\pi =\left(\pi (1),\pi (2),\dotsc ,\pi (n)\right)$

Diese Schreibweise verwendet somit lediglich die zweite Zeile der Zweizeilenform. Da so die Information über die Zahl , die auf $\pi (j)$ abgebildet wird, verloren geht, kann die Tupelschreibweise nur verwendet werden, wenn die Reihenfolge der Zahlen aus der ersten Zeile bekannt ist. In der Regel ist dies die natürliche Reihenfolge. Die Tupelschreibweise kann leicht mit der folgenden Zykelschreibweise verwechselt werden, besonders da manche Autoren die Kommata weglassen.

Beispiel

Für die obige Beispielpermutation erhält man die Tupelschreibweise

$\pi =(2,~4,~3,~1)$ .

Zykelschreibweise

Die Zykelschreibweise benötigt ebenfalls nur eine Zeile. Man beginnt mit einer beliebigen Zahl $a\in \{1,\ldots ,n\}$ und schreibt

$\left(a\;\pi (a)\;\pi ^{2}(a)\;\cdots \;\pi ^{\ell _{a}-1}(a)\right)$ ,

wobei $\pi ^{k}$ die -fache Hintereinanderausführung von $\pi$ bezeichnet und $\ell _{a}$ die kleinste natürliche Zahl mit $\pi ^{\ell _{a}}(a)=a$ ist. Eine solche Klammer heißt Zyklus und $\ell _{a}$ ist seine Länge. Gibt es weitere Zahlen, die noch nicht notiert wurden, so wählt man eine solche Zahl und schreibt einen weiteren Zyklus $(b\;\pi (b)\;\cdots \;\pi ^{\ell _{b}-1}(b))$ der Länge $\ell _{b}$ dahinter. Man fährt so lange fort, bis jede Zahl genau einmal notiert wurde. Klammern, in denen nur eine Zahl steht, können anschließend wieder gestrichen werden. Diese Darstellung ist nicht eindeutig, denn die Reihenfolge der Zyklen ist beliebig wählbar und in jedem Zyklus dürfen die Zahlen zyklisch vertauscht werden.

Beispiel

Für die obige Beispielpermutation verwendet man die folgenden Zykelschreibweisen:

$\pi =(1~2~4)(3)=(1~2~4)=(2~4~1)=(4~1~2)$

Weitere Darstellungen

Graphdarstellung

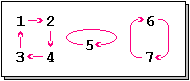
Graph der Permutation $\scriptstyle (1~2~4~3)(5)(6~7)$

Der Graph einer -stelligen Permutation $\pi$ ist ein gerichteter Graph (V,E) mit Knotenmenge $V=\{1,2,\ldots ,n\}$ und Kantenmenge

$E=\{(i,\pi (i))\mid i=1,\ldots ,n\}$ .

In einem solchen Graphen besitzt jeder Knoten genau eine ausgehende und genau eine eingehende Kante. Die Zyklen des Graphen sind gerade die Zyklen der Permutation, wobei diejenigen Zahlen, die durch die Permutation festgehalten werden, Schleifen an den zugehörigen Knoten erzeugen. Der Graph einer Permutation ist nur dann zusammenhängend, wenn die Permutation aus einem einzelnen Zyklus der Länge besteht.

Permutationsmatrizen

${\begin{pmatrix}0&1&0&0\\0&0&0&1\\0&0&1&0\\1&0&0&0\\\end{pmatrix}}$

Permutationsmatrix der Permutation $\scriptstyle (2,4,3,1)$

→ Hauptartikel: Permutationsmatrix

Die Permutationsmatrix $P_{\pi }\in \{0,1\}^{n\times n}$ einer -stelligen Permutation $\pi$ wird durch

$P_{\pi }={\begin{pmatrix}p_{11}&\dots &p_{1n}\\\vdots &\ddots &\vdots \\p_{n1}&\dots &p_{nn}\end{pmatrix}}\quad {\text{ mit }}\quad p_{ij}={\begin{cases}1,&{\text{falls }}\pi (i)=j\\0,&{\text{sonst}}\end{cases}}$

definiert. Wird durch eine Permutation die Zahl auf die Zahl $\pi (i)$ abgebildet, dann besitzt die zugehörige Permutationsmatrix in der -ten Zeile eine in der Spalte $\pi (i)$ . Die Elemente eines Spaltenvektors $(x_{1},\dotsc ,x_{n})^{T}$ werden in der linearen Algebra dadurch permutiert, dass der Vektor von links mit der Permutationsmatrix $P_{\pi }$ multipliziert wird:

$(x_{\pi (1)},\ldots ,x_{\pi (n)})^{T}=P_{\pi }\cdot (x_{1},\dotsc ,x_{n})^{T}$

Permutationen als Gruppe

Die Permutationen der Menge $\{1,2,\dotsc ,n\}$ bilden mit der Hintereinanderausführung als Verknüpfung eine Gruppe, die symmetrische Gruppe $S_{n}$ . Die symmetrischen Gruppen spielen in der Mathematik eine bedeutende Rolle. Beispielsweise ist nach dem Satz von Cayley jede endliche Gruppe zu einer Untergruppe einer symmetrischen Gruppe isomorph. Die Untergruppen der symmetrischen Gruppe heißen Permutationsgruppen.

Komposition

Zwei -stellige Permutationen $\pi ,\tau \in S_{n}$ lassen sich hintereinander ausführen, indem man zunächst die erste Permutation anwendet und auf das Resultat dann die zweite Permutation. Man schreibt die Hintereinanderausführung als

$\tau \circ \pi$ ,

wobei erst $\pi$ und dann $\tau$ angewandt wird. Diese Hintereinanderausführung wird auch Komposition, Verknüpfung oder Produkt zweier Permutationen genannt und das Ergebnis ist wieder eine -stellige Permutation. Die Komposition von Permutationen ist nicht kommutativ, das heißt im Allgemeinen liefern $\tau \circ \pi$ und $\pi \circ \tau$ verschiedene Resultate. Die symmetrische Gruppe $S_{n}$ ist demnach für n>2 nicht abelsch. Allerdings ist die Komposition assoziativ, das heißt für alle Permutationen $\pi ,\tau ,\sigma \in S_{n}$ gilt

$\sigma \circ (\tau \circ \pi )=(\sigma \circ \tau )\circ \pi$ .

Beispiele

Es ist beispielsweise

${\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}\circ {\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}}={\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}$ .

Um das Ergebnis zu erhalten, wendet man die Permutationen von rechts nach links an und verfolgt den Weg der einzelnen Zahlen. Die wird in der zweiten Permutation auf sich selbst abgebildet und in der ersten Permutation dann auf die , das heißt $1\mapsto 1\mapsto 3$ , insgesamt $1\mapsto 3$ . Der Weg der ist entsprechend $2\mapsto 3\mapsto 2$ , also $2\mapsto 2$ . Die geht schließlich den Weg $3\mapsto 2\mapsto 1$ , im Ergebnis $3\mapsto 1$ .

In der Zykeldarstellung geht man analog vor, wobei Zahlen, die nicht in einem Zyklus vorkommen, festgehalten werden. Beispielsweise ist

$(1~2~3)\circ (2~3~4)={\begin{pmatrix}1&2&3&4\\2&1&4&3\end{pmatrix}}=(1~2)(3~4)$ .

Hier ermittelt man die Wege $1\mapsto 1\mapsto 2$ , $2\mapsto 3\mapsto 1$ , $3\mapsto 4\mapsto 4$ und $4\mapsto 2\mapsto 3$ .

Identische Permutation

Das neutrale Element der symmetrischen Gruppe $S_{n}$ ist die identische Permutation

$\operatorname {id} ={\begin{pmatrix}1&2&3&\ldots &n\\1&2&3&\ldots &n\end{pmatrix}}\in S_{n}$ ,

also diejenige Permutation, die alle Zahlen an ihrem Platz belässt. Für jede Permutation $\pi \in S_{n}$ gilt damit

$\operatorname {id} \circ \,\pi =\pi \circ \operatorname {id} =\pi$ .

Die identische Permutation notiert man auch als leere Klammer , als (1) oder als $\epsilon$ . Die Permutationsmatrix der identischen Permutation ist die Einheitsmatrix. Der Graph der identischen Permutation weist lediglich eine Schleife an jedem Knoten auf. Die identische Permutation der Länge eins wird auch als triviale Permutation bezeichnet.

Inverse Permutation

Zu jeder Permutation $\pi \in S_{n}$ gibt es genau ein inverses Element, die inverse Permutation $\pi ^{-1}$ , mit

$\pi \circ \pi ^{-1}=\pi ^{-1}\circ \pi =\operatorname {id}$ .

Die inverse Permutation erhält man, indem man in der Zweizeilenform die obere mit der unteren Zeile vertauscht:

$\pi ^{-1}={\begin{pmatrix}\pi \left(1\right)&\pi \left(2\right)&\cdots &\pi \left(n\right)\\1&2&\cdots &n\end{pmatrix}}$

In der Zykelschreibweise erhält man die inverse Permutation, indem man in jedem Zyklus die Zahlen in der umgekehrten Reihenfolge schreibt. In der Graphdarstellung der inversen Permutation werden lediglich die Richtungen aller Kanten umgedreht. Die Permutationsmatrix der inversen Permutation ist die transponierte Matrix der Ausgangspermutation.

Beispiel

Die inverse Permutation zu

$\pi ={\begin{pmatrix}1&2&3&4&5\\2&4&5&1&3\end{pmatrix}}=(1~2~4)(3~5)$

ist

$\pi ^{-1}={\begin{pmatrix}2&4&5&1&3\\1&2&3&4&5\end{pmatrix}}={\begin{pmatrix}1&2&3&4&5\\4&1&5&2&3\end{pmatrix}}=(4~2~1)(5~3)$ .

Konjugation

Zwei Permutationen $\sigma ,\pi \in S_{n}$ heißen zueinander konjugiert, wenn eine Permutation $\tau \in S_{n}$ existiert, sodass

$\sigma =\tau \circ \pi \circ \tau ^{-1}$ bzw. $\sigma \circ \tau =\tau \circ \pi$

gilt. Wird durch die Permutation $\pi$ die Zahl auf die Zahl abgebildet, dann bildet die Permutation $\sigma$ die Zahl $\tau (i)$ auf die Zahl $\tau (j)$ ab. Die Konjugation stellt eine Äquivalenzrelation $\sim$ auf der Menge der Permutationen fester Länge dar, das heißt, sie ist reflexiv ( $\pi \sim \pi$ ), symmetrisch (aus $\pi \sim \sigma$ folgt $\sigma \sim \pi$ ) und transitiv (aus $\pi \sim \sigma$ und $\sigma \sim \tau$ folgt $\pi \sim \tau$ ). Die Menge aller zu einer Permutation $\pi \in S_{n}$ konjugierten Permutationen bilden eine Äquivalenzklasse (die Konjugationsklasse), die durch $\left[\pi \right]$ notiert wird.

Beispiel

Die symmetrische Gruppe $S_{3}$ besitzt die drei Konjugationsklassen:

$[\operatorname {id} ]=\{\operatorname {id} \}$

$[(1~2)]=\{(1~2),(1~3),(2~3)\}$

$[(1~2~3)]=\{(1~2~3),(1~3~2)\}$

Kenngrößen

Zykeltyp

	Zykeltyp	Zykelstruktur	Anzahl
1	1¹	( • )	1
2	1²	( • ) ( • )	1
2	2¹	( • • )	1
3	1³	( • ) ( • ) ( • )	1
	1¹ 2¹	( • • ) ( • )	3
	3¹	( • • • )	2
4	1⁴	( • ) ( • ) ( • ) ( • )	1
	1² 2¹	( • • ) ( • ) ( • )	6
	2²	( • • ) ( • • )	3
	1¹ 3¹	( • • • ) ( • )	8
	4¹	( • • • • )	6

→ Hauptartikel: Zykeltyp

Bezeichnet $b_{j}$ für $j=1,\ldots ,n$ die Anzahl der Zyklen der Länge in einer Permutation $\pi \in S_{n}$ , dann ist der Zykeltyp dieser Permutation der formale Ausdruck

$\operatorname {typ} (\pi )=1^{b_{1}}2^{b_{2}}\ldots n^{b_{n}}$ ,

wobei die Terme mit $b_{j}=0$ nicht aufgeführt werden müssen. Formal heißt hier, dass das Produkt und die Potenzen nicht tatsächlich ausgerechnet werden. Die Anzahl der möglichen Zykeltypen -stelliger Permutationen entspricht gerade der Anzahl der Partitionen der Zahl . Die Anzahl der Permutationen pro Zykeltyp kann aus der Typbeschreibung errechnet werden. Die inverse Permutation weist immer den gleichen Zykeltyp wie die Ausgangspermutation auf. Zudem hat das Resultat der Komposition zweier Permutationen unabhängig von der Reihenfolge der Operanden ebenfalls den gleichen Zykeltyp. Zwei Permutationen sind demnach genau dann zueinander konjugiert, wenn sie vom gleichen Zykeltyp sind. Die Permutationen gleichen Zykeltyps bilden daher die Konjugationsklassen der symmetrischen Gruppe $S_{n}$ . Die Permutationen mit gleicher Zyklenzahl werden durch die Stirling-Zahlen erster Art gezählt.

Ordnung

→ Hauptartikel: Elementordnung

Die Ordnung einer Permutation $\pi$ ist die kleinste natürliche Zahl derart, dass die -malige Hintereinanderausführung von $\pi$ die identische Permutation ergibt:

$\operatorname {ord} (\pi )=\min\{k\in \mathbb {N} \mid \pi ^{k}=\operatorname {id} \}$ .

Die Ordnung einer Permutation $\pi$ ist damit die Elementordnung von $\pi$ als Gruppenelement der symmetrischen Gruppe. Aus der Zykeldarstellung einer Permutation lässt sich die Ordnung als das kleinste gemeinsame Vielfache der Längen der disjunkten Zyklen ermitteln. Beispielsweise ist die Ordnung der Permutation (124)(35) das kleinste gemeinsame Vielfache von drei und zwei, also sechs.

Fehlstände

Fehlstände der Permutationen in S₃
Nr.	Permutation	Fehlstände	Anzahl
0	(1,2,3)	–	0
1	(1,3,2)	(2,3)	1
2	(2,1,3)	(1,2)	1
3	(2,3,1)	(1,3),(2,3)	2
4	(3,1,2)	(1,2),(1,3)	2
5	(3,2,1)	(1,2),(1,3),(2,3)	3

Man nennt ein Zahlenpaar (i,j) Fehlstand oder Inversion einer Permutation $\pi$ , falls i<j und $\pi (i)>\pi (j)$ gilt. Zwei Zahlen bilden also genau dann einen Fehlstand, wenn nach Anwenden der Permutation die größere vor der kleineren steht. Die Menge der Fehlstände einer Permutation $\pi \in S_{n}$ ist damit durch

$\operatorname {inv} (\pi )=\left\{(i,j)\in \{1,\ldots ,n\}^{2}\mid i<j~{\text{und}}~\pi (i)>\pi (j)\right\}$

gegeben. Die Anzahl der Fehlstände $|\operatorname {inv} (\pi )|$ einer Permutation heißt Fehlstandszahl oder Inversionszahl der Permutation. Die Fehlstandszahl kann als Maß für die Unordnung der durch die Permutation vertauschten Zahlen angesehen werden.

Vorzeichen

→ Hauptartikel: Vorzeichen (Permutation)

Das Vorzeichen oder Signum einer Permutation $\pi \in S_{n}$ ist die Zahl

$\operatorname {sgn} (\pi )=\left(-1\right)^{|\operatorname {inv} (\pi )|}$ .

Eine Permutation hat damit das Vorzeichen , falls ihre Fehlstandszahl gerade ist, ansonsten das Vorzeichen . Im ersten Fall spricht man von einer geraden und im zweiten Fall von einer ungeraden Permutation. Die Menge der geraden Permutationen bildet eine Untergruppe der symmetrischen Gruppe $S_{n}$ , die alternierende Gruppe $A_{n}$ .

Anstiege und Abstiege

Ein Anstieg in einer Permutation $\pi \in S_{n}$ ist eine Zahl , für die $\pi (i+1)>\pi (i)$ gilt. Die Menge der Anstiege in einer Permutation ist damit durch

$\operatorname {asc} (\pi )=\left\{i\in \{1,\ldots ,n-1\}\mid \pi (i+1)>\pi (i)\right\}$

gegeben. Entsprechend dazu gilt für einen Abstieg $\pi (i+1)<\pi (i)$ . Die Anzahl der Permutationen in $S_{n}$ mit genau Anstiegen bzw. Abstiegen wird durch die Euler-Zahlen $\textstyle \left\langle \!{n \atop k}\!\right\rangle$ angegeben. Eine maximale, das heißt beidseitig nicht mehr verlängerbare Folge

$(\pi (i),\pi (i+1),\ldots ,\pi (i+l))$

sukzessive steigender bzw. fallender Zahlen in einer Permutation wird ansteigender bzw. absteigender Lauf der Länge l+1 genannt. Für l=0 kann eine solche Folge auch nur aus einer Zahl bestehen. Weist eine Permutation insgesamt Anstiege bzw. Abstiege auf, so ist sie aus k+1 absteigenden bzw. ansteigenden Läufen zusammengesetzt. Demnach ist die Anzahl der Permutationen in $S_{n}$ mit genau ansteigenden bzw. absteigenden Läufen durch $\textstyle \left\langle \!{n \atop k-1}\!\right\rangle$ gegeben.

Ordnungseigenschaften

Anordnung

Hasse-Diagramm der Permutationen in S₄. Blaue, grüne und rote Kanten entsprechen den Nachbarvertauschungen (1 2), (2 3) und (3 4), die von unten nach oben gesehen immer genau einen Fehlstand erzeugen.

Mit Hilfe der Fehlstände lässt sich auf der Menge der -stelligen Permutationen eine partielle Ordnung durch

$\pi \leq \tau \Leftrightarrow \operatorname {inv} (\pi )\subseteq \operatorname {inv} (\tau )$ ,

definieren, wobei $\pi ,\tau \in S_{n}$ sind. Das minimale Element bezüglich dieser Ordnung ist die identische Permutation, während das maximale Element diejenige Permutation ist, die die Reihenfolge aller Zahlen umkehrt. In dem zugehörigen Hasse-Diagramm sind zwei Permutationen durch eine Kante verbunden, wenn sie durch eine Nachbarvertauschung auseinander hervorgehen. Die Knoten und Kanten des Hasse-Diagramms bilden einen Cayley-Graphen, der isomorph zum Kantengraphen des entsprechenden Permutaeders ist. Der Permutaeder ist ein konvexes Polytop im -dimensionalen Raum, das daraus entsteht, dass die Permutationen der Menge $\{1,\ldots ,n\}$ als Koordinatenvektoren interpretiert werden und dann die konvexe Hülle dieser Punkte gebildet wird.

Aufzählung

Die Inversionstafel oder der Inversionsvektor einer Permutation $\pi \in S_{n}$ ordnet jeder Zahl $1\leq j\leq n$ die Anzahl der Fehlstände zu, die sie erzeugt. Bezeichnet $b_{j}$ die Anzahl der Zahlen, die in der Tupeldarstellung von $\pi$ links von stehen und größer als sind, dann ist der Inversionsvektor einer Permutation durch

$I(\pi )=(b_{1},b_{2},\ldots ,b_{n})$

gegeben. Aus dem Inversionsvektor $I(\pi )$ lässt sich umgekehrt die zugrundeliegende Permutation $\pi$ eindeutig ermitteln. Fasst man die Inversionsvektor als Zahl in einem fakultätsbasierten Zahlensystem auf, lässt sich jeder Permutation $\pi \in S_{n}$ eine eindeutige Nummer $z(\pi )\in \{0,\ldots ,n!-1\}$ durch

$z(\pi )=\sum _{i=1}^{n}b_{i}\cdot (n-i)!$

zuweisen. Statt des Inversionsvektors wird auch der Lehmer-Code zur Nummerierung von Permutationen verwendet.

Symmetrien

Die zu einer Permutation $\pi \in S_{n}$ komplementäre Permutation ist

$\pi ^{-}=(n-\pi (1)+1,\ldots ,n-\pi (n)+1)$ .

Die komplementäre Permutation entsteht durch horizontale Spiegelung der Permutationsmatrix. Die reverse Permutation ist entsprechend

$\pi '=(\pi (n),\pi (n-1),\ldots ,\pi (1))$

und entsteht durch vertikale Spiegelung. Komplementäre und reverse Permutationen besitzen sie den gleichen Zykeltyp und die gleiche Ordnung wie die Ausgangspermutation. Die Zahl der An- und Abstiege wird allerdings bei komplementären und reversen Permutationen vertauscht. Außerdem kehrt sich das Vorzeichen bei komplementären Permutationen und bei reversen Permutationen mit Länge 2 modulo 4 oder Länge 3 modulo 4 um. Die Inverse der komplementären Permutation ist gleich der revertierten Inversen und die Inverse der reversen Permutation ist gleich der komplementären Inversen.

Spezielle Permutationen

Zyklische Permutationen

→ Hauptartikel: Zyklische Permutation

Graph einer zyklischen Permutation der Länge 6

Eine Permutation, die Zahlen zyklisch vertauscht und die übrigen Zahlen fest lässt, heißt zyklische Permutation oder -Zyklus und wird als ein einzelner Zyklus der Länge geschrieben. Ein -Zyklus, also eine Vertauschung zweier Zahlen, heißt auch Transposition. Die Verkettung zyklischer Permutationen ist kommutativ, wenn diese disjunkte Träger besitzen. Die Inverse einer zyklischen Permutation ist immer ebenfalls zyklisch, ebenso wie Potenzen einer zyklischen Permutation, deren Länge eine Primzahl ist. Jede zyklische Permutation kann in einzelne (nicht disjunkte) Transpositionen zerlegt werden und weist genau dann ein gerades Vorzeichen auf, wenn ihre Länge ungerade ist.

Fixpunktfreie Permutationen

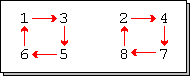
→ Hauptartikel: Fixpunktfreie Permutation

Graph einer fixpunktfreien Permutation der Zahlen von 1 bis 8

Zahlen, die durch eine Permutation festgehalten werden, nennt man Fixpunkte der Permutation. In der Zweizeilenform erkennt man Fixpunkte daran, dass der obere und untere Eintrag der jeweiligen Spalte gleich ist. In der Zykelschreibweise sind Fixpunkte genau die Einerzyklen beziehungsweise die Zahlen, die nicht erscheinen. In der Permutationsmatrix sind die den Fixpunkten zugewiesenen Einträge der Hauptdiagonale . Eine fixpunktfreie Permutation hält keine der Zahlen fest und wird auch Derangement genannt. Die Anzahl der fixpunktfreien Permutationen der Zahlen von bis kann durch die Subfakultät {!}n berechnet werden. Für wachsendes strebt der Anteil der fixpunktfreien Permutationen sehr schnell gegen den Kehrwert der eulerschen Zahl . Sollen in einer Permutation manche der Elemente an ihrem alten Platz verbleiben, spricht man von einem partiellen Derangement, deren Anzahl durch die Rencontres-Zahlen ermittelt werden kann.

Selbstinverse Permutationen

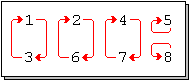
→ Hauptartikel: Selbstinverse Permutation

Graph einer selbstinversen Permutation der Zahlen von 1 bis 8

Eine Permutation $\pi$ mit $\pi ^{2}={\mbox{id}}$ oder äquivalent dazu $\pi ^{-1}=\pi$ heißt Involution oder selbstinvers. Die Involutionen sind genau die Permutationen der Ordnung zwei sowie die Identität selbst (die einzige Permutation der Ordnung eins). Eine Permutation ist genau dann eine Involution, wenn ihre Zykeldarstellung maximal Zyklen der Länge zwei, also Transpositionen, enthält. Die Permutationsmatrix einer selbstinversen Permutation ist immer symmetrisch. Selbstinverse Permutationen spielen in der Kryptographie eine wichtige Rolle, wird nämlich eine Nachricht mit Hilfe einer selbstinversen Permutation verschlüsselt, dann lässt sich die Nachricht mittels der gleichen Permutation auch wieder entschlüsseln.

Alternierende Permutationen

Man nennt eine Permutation alternierend, wenn in ihrer Tupeldarstellung keine Zahl $\pi (j)$ von ihrer Größe her zwischen der vorangehenden Zahl $\pi (j-1)$ und der nachfolgenden Zahl $\pi (j+1)$ steht. In einer alternierenden Permutation sind demnach die durch die Permutation vertauschten Zahlen immer abwechselnd größer und kleiner als die jeweils vorangegangene Zahl. Beginnt die Folge der Zahlen mit einem Anstieg, so spricht man von einer Up-Down-Permutation, beginnt sie mit einem Abstieg von einer Down-Up-Permutation. Jede alternierende Permutation ungerader Länge entspricht einem vollen partiell geordneten Binärbaum und jede alternierende Permutation gerader Länge einem fast vollen solchen Baum. Die Anzahlen der alternierenden Permutationen fester Länge treten als Koeffizienten in der Maclaurin-Reihe der Sekans- und der Tangensfunktion auf und stehen in engem Zusammenhang mit den Euler- und den Bernoulli-Zahlen.

Separable Permutationen

Separable Permutationen sind Permutationen, die sich als direkte oder schiefe Summe trivialer Permutationen darstellen lassen. Eine solche Summe zweier Permutationen ergibt eine neue Permutation, deren Länge die Summe der Längen der beiden Ausgangspermutationen ist. Bei einer direkten Summe wird dabei die zweite Permutation verschoben an die erste angehängt, bei einer schiefen Summe die erste Permutation verschoben der zweiten vorangestellt. Die Anzahl separabler Permutationen fester Länge wird durch die Schröder-Zahlen angegeben. Separable Permutationen zeichnen sich durch eine spezielle rekursive Blockstruktur der zugehörigen Permutationsmatrizen aus. Sie werden unter anderem in der Sortierungstheorie untersucht.

Zufällige Permutationen

Eine zufällige Permutation ist eine aus der Menge der Permutationen $S_{n}$ zufällig ausgewählte Permutation. In der Stochastik werden zufällige Permutationen als Zufallsvariablen aus einem diskreten Wahrscheinlichkeitsraum angesehen. So können auch Kennzahlen zufälliger Permutationen, wie die Anzahl der Fixpunkte, Fehlstände oder Zyklen, als diskrete Zufallsvariablen angesehen werden, deren Wahrscheinlichkeitsverteilungen dann untersucht werden. Im Computer können zufällige Permutationen effizient mit dem Fisher-Yates-Verfahren generiert werden. Zufällige Permutationen werden unter anderem bei der Analyse von Sortierverfahren, in der Kryptographie und Kodierungstheorie sowie im Rahmen randomisierter Algorithmen untersucht. Das Problem der 100 Gefangenen ist ein mathematisches Rätsel, das auf zufälligen Permutationen basiert.

Basierend auf einem Artikel in:

Wikipedia.de