Vorzeichen (Permutation)

Das Vorzeichen, auch Signum, Signatur oder Parität genannt, ist in der Kombinatorik eine wichtige Kennzahl von Permutationen. Das Signum einer Permutation kann die Werte oder annehmen, wobei man im ersten Fall von einer geraden und im zweiten Fall von einer ungeraden Permutation spricht.

Es gibt mehrere Möglichkeiten, gerade und ungerade Permutationen zu charakterisieren. So ist eine Permutation genau dann gerade, wenn die Anzahl der Fehlstände in der Permutation gerade ist. Jede Permutation lässt sich auch als Verkettung endlich vieler Transpositionen darstellen und ist genau dann gerade, wenn die Anzahl der dabei benötigten Transpositionen gerade ist. Eine Permutation kann zudem auch in Zyklen zerlegt werden und ist genau dann gerade, wenn die Anzahl der Zyklen gerader Länge gerade ist. Das Signum einer Permutation ist auch gleich der Determinante der zugehörigen Permutationsmatrix.

Das Signum ist als Abbildung ein Gruppenhomomorphismus von der symmetrischen Gruppe der Permutationen in die multiplikative Gruppe über der Menge $\{ +1, -1 \}$ . Ein wichtiges Einsatzbeispiel des Signums ist die Leibniz-Formel für Determinanten.

Definition

Ist $S_{n}$ die symmetrische Gruppe aller Permutationen der Menge $\{1,\ldots ,n\}$ , dann wird das Vorzeichen einer Permutation $\pi = ( \pi(1), \pi(2), \ldots , \pi(n) ) \in S_n$ durch

$\operatorname {sgn}(\pi )=(-1)^{|\operatorname {inv} (\pi )|}$

definiert, wobei

$\operatorname{inv}(\pi) = \{~ (i,j) \in \{ 1, \ldots , n \} \times \{ 1, \ldots , n \} \mid i < j, \pi(i) > \pi(j) ~\}$

die Menge der Fehlstände der Permutation ist. Ist das Vorzeichen nennt man die Permutation $\pi$ gerade, ist es nennt man sie ungerade.

Allgemeiner können auch Permutationen beliebiger endlicher geordneter Mengen betrachtet werden, für die mathematische Analyse kann man sich jedoch auf die ersten natürlichen Zahlen beschränken.

Beispiele

Permutationen in S₃
Permutation	Fehlstände	Signum
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 1 ~ 2 ~ 3 \,}$	–	+1
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 1 ~ 3 ~ 2 \,}$	(2,3)	−1
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 2 ~ 1 ~ 3 \,}$	(1,2)	−1
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 2 ~ 3 ~ 1 \,}$	(1,3),(2,3)	+1
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 3 ~ 1 ~ 2 \,}$	(1,2),(1,3)	+1
$\tbinom{\, 1 ~ 2 ~ 3 \,}{\, 3 ~ 2 ~ 1 \,}$	(1,2),(1,3),(2,3)	−1

Die Fehlstände der Permutation

$\pi = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 1 & 4 & 5 & 3\end{pmatrix} \in S_5$

sind (1,2), (3,5) und (4,5) , somit ist

$\operatorname {sgn}(\pi )=(-1)^{3}=-1$

und damit die Permutation ungerade. Die identische Permutation

$\operatorname{id} = \begin{pmatrix} 1 & 2 & \cdots & n \\ 1 & 2 & \cdots & n \end{pmatrix} \in S_n$

ist immer gerade, denn sie weist keine Fehlstände auf. Die nebenstehende Tabelle führt alle Permutationen der Länge drei mit ihren zugehörigen Vorzeichen auf.

Darstellung als Produkt

Produktformel

Das Vorzeichen einer Permutation der ersten natürlichen Zahlen kann auch durch die Produktformel

$\operatorname {sgn}(\pi )=\prod _{1\leq i<j\leq n}{\frac {\pi (j)-\pi (i)}{j-i}}$

dargestellt werden. Aufgrund der Bijektivität einer Permutation tritt hierbei jeder Term j-i für $1\le i<j\le n$ bis auf gegebenenfalls das Vorzeichen je einmal im Zähler und einmal Nenner eines Bruchs auf. Jeder Fehlstand führt dabei zu genau einem negativen Vorzeichen.

Beispiel

Das Signum der Permutation

$\pi = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} \in S_3$

ist durch

${\begin{aligned}\operatorname {sgn}(\pi )&={\frac {\pi (2)-\pi (1)}{2-1}}\cdot {\frac {\pi (3)-\pi (1)}{3-1}}\cdot {\frac {\pi (3)-\pi (2)}{3-2}}\\&={\frac {1-3}{2-1}}\cdot {\frac {2-3}{3-1}}\cdot {\frac {2-1}{3-2}}\\&={\frac {2-1}{2-1}}\cdot {\frac {1-3}{3-1}}\cdot {\frac {2-3}{3-2}}\\&=(+1)\cdot (-1)\cdot (-1)=+1\end{aligned}}$

gegeben. Die beiden Fehlstände (1,2) und (1,3) führen dabei zu jeweils einem Vorzeichenwechsel.

Verkettungseigenschaft

Für das Signum einer Verkettung zweier Permutationen $\tau, \pi \in S_n$ gilt aufgrund der Produktdarstellung:

${\begin{aligned}\operatorname {sgn}(\tau \circ \pi )&=\prod _{i<j}{\frac {\tau (\pi (j))-\tau (\pi (i))}{j-i}}=\prod _{i<j}{\frac {\tau (\pi (j))-\tau (\pi (i))}{\pi (j)-\pi (i)}}\cdot \prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\\&=\prod _{\pi ^{-1}(i)<\pi ^{-1}(j)}{\frac {\tau (j)-\tau (i)}{j-i}}\cdot \prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\operatorname {sgn}(\tau )\cdot \operatorname {sgn}(\pi )\end{aligned}}$

Der letzte Schritt folgt daraus, dass in dem Produkt über $\pi^{-1}(i) < \pi^{-1}(j)$ die gleichen Faktoren, wie in dem Produkt über i<j vorkommen, nur in anderer Reihenfolge. Für zwei durch $\pi$ vertauschte Zahlen i,j kehrt sich dabei sowohl im Nenner und im Zähler das Vorzeichen um. Demnach ist die Verkettung zweier Permutationen genau dann gerade, wenn beide Permutationen das gleiche Signum aufweisen.

Weitere Darstellungen

Darstellung über die Zahl der Transpositionen

Umwandlung zwischen geraden und ungeraden Permutationen durch Transpositionen

Eine Transposition $\tau_{kl}$ mit k<l ist eine Permutation, die lediglich die zwei Zahlen und vertauscht, das heißt auf sowie auf abbildet und die übrigen Zahlen festlässt. Für das Signum einer Transposition gilt

$\operatorname {sgn}(\tau _{kl})=-1$ ,

denn jede Transposition lässt sich als Verkettung einer ungeraden Zahl von Nachbarvertauschungen der Form $\tau_{k,k+1}$ durch

$\tau_{kl} = (\tau_{l-1,l} \circ \tau_{l-2,l-1} \circ \cdots \circ \tau_{k+1,k+2}) \circ (\tau_{k,k+1} \circ \cdots \circ \tau_{l-2,l-1} \circ \tau_{l-1,l})$

darstellen. Hierbei wird zunächst die Zahl durch sukzessive Nachbarvertauschungen an die Stelle gebracht und dann die Zahl von der Stelle k+1 durch sukzessive Nachbarvertauschungen an die Stelle . Nachdem jede dieser Nachbarvertauschungen genau einen Fehlstand erzeugt, ist die Gesamtzahl der Fehlstände einer Transposition

$| \operatorname{inv}(\tau_{kl}) | = (l-k) + (l-k-1) = 2(l-k)-1$

und damit immer ungerade. Jede Permutation $\pi \in S_{n}$ lässt sich nun als Verkettung von höchstens n-1 Transpositionen darstellen. Jede dieser Transpositionen vertauscht dabei jeweils die kleinste Zahl , für die $\pi(k) \neq k$ gilt, mit derjenigen Zahl l>k , für die $\pi(l) = k$ gilt. Ist $M(\pi)$ die Anzahl der dabei benötigten Transpositionen, dann gilt aufgrund der Verkettungseigenschaft

$\operatorname {sgn}(\pi )=(-1)^{M(\pi )}$ .

Es gibt natürlich noch weitere Möglichkeiten, eine Permutation als Verkettung von Transpositionen darzustellen. Handelt es sich dabei aber um eine gerade Permutation, dann ist die Zahl der benötigten Transpositionen immer gerade, handelt es sich um eine ungerade Permutation immer ungerade.

Beispiel

Die Permutation

$\pi = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 2 & 4 & 1\end{pmatrix} \in S_4$

lässt sich durch

$\pi = \tau_{34} \circ \tau_{14} = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 4 & 3\end{pmatrix} \circ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 2 & 3 & 1\end{pmatrix}$

darstellen und ist damit gerade. Eine weitere Darstellung von $\pi$ als Verkettung von Transpositionen wäre etwa $\pi = \tau_{23} \circ \tau_{12} \circ \tau_{23} \circ \tau_{34}$ .

Darstellung über die Zahl und Länge der Zyklen


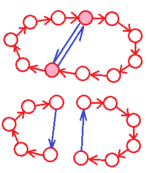
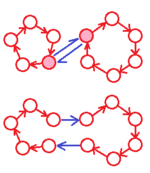
Durch die Hintereinanderausführung einer Permutation (rot) mit einer Vertauschung (blau) erhöht sich die Anzahl der Zyklen um eins, wenn die vertauschten Elemente innerhalb eines Zyklus liegen (links) und sie verringert sich um eins, wenn sie in verschiedenen Zyklen liegen (rechts).

Eine zyklische Permutation $\sigma_{k_1, \ldots, k_m}$ ist eine Permutation, die die Zahlen $k_1, \ldots , k_m$ zyklisch vertauscht, das heißt $k_{1}$ auf $k_{2}$ abbildet, $k_{2}$ auf k_3 bis hin zu k_m auf $k_{1}$ und die übrigen Zahlen festlässt. Eine zyklische Permutation der Länge zwei entspricht gerade einer Transposition zweier Zahlen. Jede zyklische Permutation der Länge m>1 kann als Verkettung von m-1 Transpositionen geschrieben werden:

$\sigma_{k_1, \ldots, k_m} = \tau_{k_1,k_2} \circ \cdots \circ \tau_{k_{m-1},k_m}$ .

Da Transpositionen ungerade sind, ist das Signum einer zyklischen Permutation der Länge aufgrund der Verkettungseigenschaft

$\operatorname {sgn}(\sigma _{k_{1},\ldots ,k_{m}})=\operatorname {sgn}(\tau _{k_{1},k_{2}})\cdot \ldots \cdot \operatorname {sgn}(\tau _{k_{m-1},k_{m}})=(-1)^{m-1}$ .

Eine zyklische Permutation ist also genau dann gerade, wenn ihre Länge ungerade ist. Jede Permutation $\pi \in S_{n}$ lässt sich nun eindeutig als Verkettung von $s \leq n$ zyklischen Permutationen mit paarweise disjunkten Zyklen darstellen. Sind $m_1, \ldots , m_s$ die Längen dieser Zyklen, dann gilt aufgrund der Verkettungseigenschaft

$\operatorname {sgn}(\pi )=(-1)^{m_{1}-1}\cdot \ldots \cdot (-1)^{m_{s}-1}=(-1)^{m_{1}+\ldots +m_{s}-s}$ .

Das Signum kann daher direkt aus dem Zykeltyp der Permutation abgelesen werden. Eine Permutation ist demnach genau dann gerade, wenn die Summe der Längen der einzelnen Zyklen minus der Anzahl der Zyklen gerade ist. Da Zyklen ungerader Länge das Signum nicht verändern, ist eine Permutation genau dann gerade, wenn die Anzahl der Zyklen gerader Länge gerade ist. Nachdem sich die Ordnung einer Permutation aus dem kleinsten gemeinsamen Vielfachen ihrer Zyklenlängen ergibt, ist eine Permutation mit ungerader Ordnung stets gerade.

Beispiel

Die Permutation

$\pi = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 3 & 6 & 4 & 1 & 5 & 2 \end{pmatrix} \in S_6$

zerfällt in drei disjunkte Zyklen, in Zykelschreibweise

$\pi = (1 ~ 3 ~ 4)(2 ~ 6)(5)$ .

Da die Summe 3+2+1-3 ungerade ist, ist die Permutation ebenfalls ungerade. Einerzyklen können in der Zykelschreibweise und bei der Zählung auch weggelassen werden, ohne die Summe und damit das Signum zu verändern.

Darstellung über die Determinante der Permutationsmatrix

Ist $P_\pi \in \{ 0,1 \}^{n \times n}$ die zu der Permutation $\pi \in S_{n}$ zugehörige Permutationsmatrix mit Einträgen

$(P_\pi)_{ij} = \begin{cases} 1, & \text{falls } \pi(i)=j \\ 0, & \text{sonst,}\end{cases}$

dann entspricht das Signum von $\pi$ gerade der Determinante von $P_{\pi }$ , also

$\operatorname {sgn}(\pi )=\det(P_{\pi })$ .

Zur praktischen Berechnung des Signums ist diese Darstellung allerdings meist ungeeignet.

Beispiel

Die zur Permutation

$\pi = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} \in S_3$

zugehörige Permutationsmatrix ist

$P_\pi = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix}$ ,

deren Determinante sich nach der Regel von Sarrus zu

$\det(P_\pi) = (0 +0 +1) -(0 +0 +0) = +1$

ergibt.

Weitere Eigenschaften

Mächtigkeiten

Es gibt genau verschiedene Permutationen der Menge $\{1,\ldots ,n\}$ . Für $n\geq 2$ wird die Menge aller Permutationen durch die geraden und ungeraden Permutationen in zwei gleich große Hälften geteilt, denn es gibt gleich viele Möglichkeiten, die Vorzeichen im Zähler der Produktformel so zu wählen, dass das Produkt positiv bzw. negativ ist. Für die Mächtigkeit dieser beiden Mengen gilt demnach

$\#\{\pi \in S_{n}\mid \operatorname {sgn}(\pi )=+1\}=\#\{\pi \in S_{n}\mid \operatorname {sgn}(\pi )=-1\}={\frac {n!}{2}}$ .

Aus diesem Grund spricht man hier neben dem Signum auch von der Parität (von lateinisch paritas Gleichheit) einer Permutation.

Inverse Permutationen

Für das Signum der inversen Permutation $\pi ^{-1}$ von $\pi$ gilt:

$\operatorname {sgn}(\pi ^{-1})=\prod _{i<j}{\frac {j-i}{\pi (j)-\pi (i)}}=\prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\operatorname {sgn}(\pi )$ .

Durch Invertierung ändert sich also das Signum einer Permutation nicht, was mit der Verkettungseigenschaft auch direkt über

$\operatorname {sgn}(\pi ^{-1})\cdot \operatorname {sgn}(\pi )=\operatorname {sgn}(\pi ^{-1}\circ \pi )=\operatorname {sgn}(\operatorname {id} )=1$

ersichtlich ist.

Signum-Homomorphismus

Aufgrund der Verkettungseigenschaft stellt die Abbildung

$\operatorname {sgn} \colon S_{n}\to \{+1,-1\}$

einen Gruppenhomomorphismus von der symmetrischen Gruppe $(S_n, \circ)$ in die multiplikative Gruppe $(\{ +1, -1 \}, \cdot)$ dar (dies ist gerade die zyklische Gruppe vom Grad 2). Diese Eigenschaft wird in der Theorie der Determinanten, beispielsweise der Leibniz-Formel verwendet. Der Kern dieses Homomorphismus ist die Menge der geraden Permutationen. Sie bildet einen Normalteiler von $S_{n}$ , die alternierende Gruppe $A_{n}$ . Die Menge der ungeraden Permutationen bildet jedoch keine Untergruppe von $S_{n}$ , denn die Verkettung zweier ungerader Permutationen ergibt eine gerade Permutation.

Konjugierte Permutationen besitzen dasselbe Signum, wie aus den Eigenschaften des Signum-Homomorphismus folgt. Ist nämlich $\sigma \in S_n$ , dann gilt für alle $\pi \in S_{n}$

$\operatorname {sgn}(\pi \circ \sigma \circ \pi ^{-1})=\operatorname {sgn}(\pi )\cdot \operatorname {sgn}(\sigma )\cdot \operatorname {sgn}(\pi ^{-1})=\operatorname {sgn}(\pi )\cdot \operatorname {sgn}(\pi )^{-1}\cdot \operatorname {sgn}(\sigma )=\operatorname {sgn}(\sigma )$ .

Verwendung

Das Vorzeichen von Permutationen wird unter anderem in folgenden Bereichen verwendet:

bei der Charakterisierung der Determinante einer Matrix über die Leibniz-Formel
bei der Definition antisymmetrischer Funktionen, beispielsweise alternierender Multilinearformen
bei dem Lemma von Zolotareff zur Darstellung des Legendre-Symbols

Verallgemeinerung

Eine Verallgemeinerung des Signums für nicht notwendigerweise bijektive Abbildungen $\phi \colon \{ 1, \ldots , n \} \to \{ 1, \ldots , n \}$ ist das Levi-Civita-Symbol $\varepsilon_{\phi_1 \ldots \phi_n}$ , das mit der Notation $\phi_k = \phi(k)$ für $k = 1 , \ldots , n$ wie das Signum über

$\varepsilon_{\phi_1 \ldots \phi_n} = \prod_{1 \leq i < j \leq n} \frac{\phi_j-\phi_i}{j-i}$

definiert werden kann. Im Unterschied zum Signum kann das Levi-Civita-Symbol jedoch auch den Wert $0$ annehmen, was genau dann der Fall ist, wenn die Abbildung $\phi$ nicht bijektiv ist. Das Levi-Civita-Symbol wird insbesondere in der Vektor- und Tensorrechnung in Anwendungen wie der Relativitätstheorie und der Quantenmechanik verwendet.

Basierend auf einem Artikel in:

Wikipedia.de