Abzählende Kombinatorik

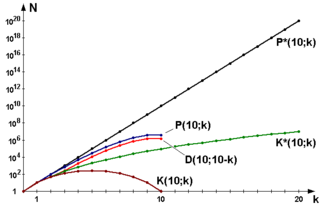
Zahl der Variationen und Kombinationen von 10 Elementen zur k-ten Klasse und der partiellen Derangements (fixpunktfreie Permutationen) von 10 Elementen.
P*(10;k) k-Permutationen oder Variationen mit Wiederholung
P(10;k) k-Permutationen oder Variationen ohne Wiederholung
K*(10;k) k-Kombinationen mit Wiederholung
K(10;k) k-Kombinationen ohne Wiederholung
D(10;10-k) partielle Derangements
(bei denen nur k der 10 Elemente die Plätze wechseln)

Die abzählende Kombinatorik ist ein Teilbereich der Kombinatorik. Sie beschäftigt sich mit der Bestimmung der Anzahl möglicher Anordnungen oder Auswahlen

unterscheidbarer oder nicht unterscheidbarer Objekte (d.h. „ohne“ bzw. „mit“ Wiederholung derselben Objekte) sowie
mit oder ohne Beachtung ihrer Reihenfolge (d.h. „geordnet“ bzw. „ungeordnet“).

In der modernen Kombinatorik werden diese Auswahlen oder Anordnungen auch als Abbildungen betrachtet, so dass sich die Aufgabe der Kombinatorik in diesem Zusammenhang im Wesentlichen darauf beschränken kann, diese Abbildungen zu zählen.

Anwendungen

Für das Rechnen mit Wahrscheinlichkeiten auf der Basis des Wahrscheinlichkeitsbegriffs von Pierre-Simon Laplace bildet die Kombinatorik eine wichtige Grundlage.

Ein verblüffendes Phänomen der Kombinatorik ist, dass sich oftmals wenige Objekte auf vielfältige Weise kombinieren lassen. Beim Zauberwürfel können beispielsweise die 26 Elemente auf rund 43 Trillionen Arten kombiniert werden. Dieses Phänomen wird oft als kombinatorische Explosion bezeichnet und ist auch die Ursache für das Geburtstagsparadoxon.

Permutationen, Variationen und Kombinationen

→ Hauptartikel: Permutation, Variation (Kombinatorik) und Kombination (Kombinatorik)

Begriffsabgrenzungen

Aufgrund der Vielfalt der Herangehensweisen sind die Schreibweisen und Begrifflichkeiten im Bereich der Kombinatorik leider oft recht uneinheitlich. Zwar bezeichnen übereinstimmend alle Autoren die Vertauschung der Reihenfolge einer Menge von unterscheidbaren Elementen als Permutation. Wählt man dagegen von diesen Elementen nur k<n Elemente aus, deren Reihenfolge man anschließend vertauscht, bezeichnen viele Autoren das nun als Variation, geordnete Stichprobe bzw. Kombination mit Berücksichtigung der Reihenfolge, andere dagegen (namentlich im englischsprachigen Raum) weiter als Permutation. Lässt man schließlich in einer solchen Auswahl von Elementen deren Reihenfolge außer Acht, wird solch eine Auswahl nun für gewöhnlich ungeordnete Stichprobe, Kombination ohne Berücksichtigung der Reihenfolge oder einfach nur Kombination genannt. Kombinationen sind also, sofern nichts weiter zu ihnen gesagt wird, in der Regel ungeordnet, Permutationen und/oder Variationen dagegen geordnet, wobei die Frage, ob man Permutationen als Sonderfälle von Variationen (oder umgekehrt) betrachtet, gegebenenfalls von Autor zu Autor unterschiedlich beantwortet wird.

Alles in allem gibt es also zunächst einmal drei (oder auch nur zwei) verschiedene Fragestellungen, die ihrerseits noch einmal danach unterteilt werden, ob es unter den ausgewählten Elementen auch Wiederholungen gleicher Elemente geben darf oder nicht. Ist ersteres der Fall, spricht man von Kombinationen, Variationen oder Permutationen mit Wiederholung, andernfalls solchen ohne Wiederholung. Stellt man sich schließlich vor, dass die ausgewählten Elemente dabei einer Urne oder Ähnlichem entnommen werden, wird dementsprechend auch von Stichproben mit oder ohne Zurücklegen gesprochen:

	Ohne Wiederholung bzw. Zurücklegen	Mit Wiederholung bzw. Zurücklegen
Mit Berücksichtigung der Reihenfolge und k = n	Permutation ohne Wiederholung (engl. n-permutation)	Permutation mit Wiederholung
Mit Berücksichtigung der Reihenfolge und k < n	Variation ohne Wiederholung (engl. k-permutation)	Variation mit Wiederholung
Ohne Berücksichtigung der Reihenfolge und k < n	Kombination ohne Wiederholung (engl. k-combination)	Kombination mit Wiederholung

Anzahlen

Bezeichnet die Zahl der vorhandenen Elemente und $k_{1},\ldots ,k_{s}$ die jeweiligen Anzahlen der Elemente, die nicht unterscheidbar sind, dann gilt für die Anzahl möglicher Permutationen:

	ohne Wiederholung/Zurücklegen	mit Wiederholung/Zurücklegen
Permutation $(a,b)\neq (b,a)$		${\frac {(k_{1}+\ldots +k_{s})!}{k_{1}!\cdot \ldots \cdot k_{s}!}}={\frac {n!}{k_{1}!\cdot \ldots \cdot k_{s}!}}={\binom {n}{k_{1},\ldots ,k_{s}}}$

Bezeichnet die Zahl der vorhandenen Elemente und die Zahl der Elemente, die ausgewählt werden, dann gilt für die Anzahl möglicher Variationen und Kombinationen (für die Schreibweise $\left(\!\tbinom{n}{k}\!\right)$ siehe auch Multimenge):

	ohne Wiederholung/Zurücklegen $(a,b,c),\{a,b,c\}$	mit Wiederholung/Zurücklegen $(a,a,b),\{a,a,b\}$
Variation $(a,b)\neq (b,a)$	${n \choose k}\cdot {k!}={\frac {n!}{\left(n-k\right)!}}$	$~n^{k}~$
Kombination $\{a,b\}=\{b,a\}$	${n \choose k}={\frac {n!}{{\left(n-k\right)!}\cdot k!}}$	$\left(\!\!{n \choose k}\!\!\right)={n+k-1 \choose k}={\frac {\left(n+k-1\right)!}{\left(n-1\right)!\cdot k!}}$

Bälle und Fächer

Eine Verallgemeinerung des Urnenmodells ist ein von Gian-Carlo Rota popularisiertes Modell mit Bällen und Fächern, im Englischen nach einem Vorschlag von Joel H. Spencer auch Twelvefold Way („Zwölffacher Weg“) genannt. Gesucht ist dabei die Anzahl der Möglichkeiten, Bälle auf Fächer zu verteilen, wobei die Bälle und Fächer jeweils entweder unterscheidbar oder nicht unterscheidbar sind und entweder keine weitere Bedingung gilt oder in jedes Fach höchstens ein Ball kommen darf oder mindestens ein Ball kommen muss. Man erhält folgende Übersicht:

Bälle	Fächer	Beschränkung auf Anzahl der Bälle pro Fach
unterscheidbar?		—	max. 1	mind. 1
$\checkmark$	$\checkmark$	$n^{k}$	${\tfrac {n!}{(n-k)!}}=k!\,{\tbinom {n}{k}}$	$n!\,S_{k,n}$
$\times$	$\checkmark$	$\left(\!\!{\tbinom {n}{k}}\!\!\right)={\tbinom {k+n-1}{n-1}}$	${\tbinom {n}{k}}$	$\left(\!\!{\tbinom {n}{k-n}}\!\!\right)={\tbinom {k-1}{n-1}}$
$\checkmark$	$\times$	$\sum _{r=0}^{n}S_{k,r}$	${\begin{array}{lll}1&:&k\leq n\\0&:&k>n\end{array}}$	$S_{k,n}$
$\times$	$\times$	$\sum _{r=0}^{n}P_{k,r}=P_{k+n,n}$	${\begin{array}{lll}1&:&k\leq n\\0&:&k>n\end{array}}$	$P_{k,n}$

Dabei ist $S_{k,n}$ die Anzahl der Möglichkeiten, eine -elementige Menge in nichtleere disjunkte Teilmengen aufzuteilen (Stirling-Zahl zweiter Art), und $P_{k,n}$ die Anzahl der Möglichkeiten, die Zahl als Summe von positiven ganzen Zahlen ohne Beachtung der Reihenfolge darzustellen (siehe Partitionsfunktion).

Äquivalente Darstellungen

Wird in einem diskreten Wahrscheinlichkeitsraum $(\Omega ,P)$ die Anzahl der möglichen Ereignisse durch eine der obigen kombinatorischen Formeln gegeben, dann können über die vollständige Zerlegung des Ereignisraums äquivalente Darstellungen für sie abgeleitet werden. Die folgenden beiden Modelle verdeutlichen dies. Es werden Bälle zufällig auf $n\leq k$ Fächer verteilt. Man betrachte die Ereignisse $E_{j}$ , dass Fächer, $j=1,\ldots ,n$ , mindestens einen Ball enthalten unter der Prämisse:

Kein Ball wird von vornherein einem Fach zugeordnet.
Jeder Ball wird von vornherein einem Fach zugeordnet, kann aber in einem anderen Fach landen.

Der erste Fall entspricht der Variante „nicht unterscheidbare Bälle, unterscheidbare Fächer“. Die vollständige Zerlegung des Ereignisraums in die disjunkten Ereignisse $E_{j}$ ergibt dann

$|\Omega |={\binom {n+k-1}{k}}=\sum _{j=1}^{n}{\binom {n}{j}}{\binom {k-1}{k-j}}$ .

Der zweite Fall entspricht der Variante „unterscheidbare Bälle, unterscheidbare Fächer“. Die vollständige Zerlegung des Ereignisraums analog zum ersten Fall ergibt die äquivalente Darstellung

$|\Omega |=n^{k}=\sum _{j=1}^{n}{\binom {n}{j}}\sum _{i=0}^{j-1}(-1)^{i}{\binom {j}{j-i}}(j-i)^{k}$ .

Für n=k ist das Ereignis, dass alle Fächer mindestens einen Ball besitzen, gleich dem Ereignis, dass alle Fächer genau einen Ball besitzen, und enthält Elemente. Daraus folgt

$n!=\sum _{i=0}^{n-1}(-1)^{i}{\binom {n}{n-i}}(n-i)^{n}$ .

Basierend auf einem Artikel in:

Wikipedia.de