Erzeugendensystem

Ein Erzeugendensystem ist in der Mathematik eine Teilmenge der Grundmenge einer mathematischen Struktur, aus der durch Anwendung der verfügbaren Operationen jedes Element der gesamten Menge dargestellt werden kann. Speziell heißt das im Fall von Vektorräumen, dass jeder Vektor als Linearkombination von Vektoren des Erzeugendensystems dargestellt werden kann. Im Fall von Gruppen bedeutet dies, dass jedes Gruppenelement als Produkt aus Elementen des Erzeugendensystems und deren Inversen dargestellt werden kann. Es gibt den Begriff des Erzeugendensystems aber auch für weitere algebraische Strukturen, wie Moduln und Ringe, und auch für nichtalgebraische Strukturen, wie topologische Räume.

Das Erzeugendensystem einer vorgegebenen mathematischen Struktur ist in der Regel nicht eindeutig bestimmt. Die Existenz eines Erzeugendensystems ist hingegen meist leicht zu zeigen, da oft die Grundmenge selbst als Erzeugendensystem gewählt werden kann. Häufig wird daher versucht, ein minimales Erzeugendensystem zu finden. Dies ist jedoch nicht immer möglich und allgemeine Existenzbeweise für minimale Erzeugendensysteme machen nicht selten vom zornschen Lemma Gebrauch (siehe beispielsweise die Existenz einer Basis in Vektorräumen).

Allgemein lässt sich auch die von einer beliebigen Teilmenge erzeugte Unterstruktur einer mathematischen Struktur betrachten. Diese Unterstruktur wird Erzeugnis dieser Teilmenge genannt und die Teilmenge selbst heißt dann erzeugende Menge oder Erzeuger der Unterstruktur. So ist jeder Untervektorraum das Erzeugnis einer erzeugenden Menge von Vektoren (nämlich gerade die lineare Hülle dieser Vektoren) und jede Untergruppe das Erzeugnis einer erzeugenden Menge von Gruppenelementen.

Erzeugendensysteme in der linearen Algebra

Definition

Ist ein Vektorraum über einem Körper , dann heißt eine Menge $E\subseteq V$ Erzeugendensystem von , falls jeder Vektor aus als Linearkombination von Vektoren aus darstellbar ist. Jeder Vektor $v\in V$ besitzt demnach eine Zerlegung der Form

$v=\lambda _{1}e_{1}+\dotsb +\lambda _{n}e_{n}$

mit $n \in \N_0$ , $\lambda _{1},\dotsc ,\lambda _{n}\in K$ und $e_{1},\dotsc ,e_{n}\in E$ . Eine solche Zerlegung ist im Allgemeinen nicht eindeutig bestimmt. Ein Vektorraum heißt endlich erzeugt, wenn er ein Erzeugendensystem aus endlich vielen Vektoren besitzt.

Beispiele

Koordinatenraum

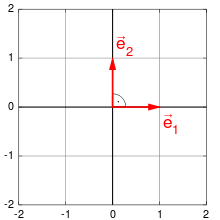
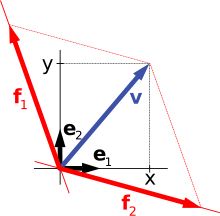
Standardbasisvektoren in der euklidischen Ebene

Zwei unterschiedliche Erzeugendensysteme: der Vektor lässt sich durch $v=xe_{1}+ye_{2}$ oder durch $v=f_{1}+f_{2}$ darstellen.

Ein Erzeugendensystem des reellen Koordinatenraums $V=\R^n$ besteht aus den sogenannten Standardbasisvektoren

$e_{1}=(1,0,0,\dotsc ,0),e_{2}=(0,1,0,\dotsc ,0),\dotsc ,e_{n}=(0,0,0,\dotsc ,1)$ .

Tatsächlich lässt sich jeder Vektor $v=(v_{1},\dotsc ,v_{n})\in \mathbb {R} ^{n}$ durch

$v=v_{1}e_{1}+v_{2}e_{2}+\dotsb +v_{n}e_{n}$

mit $v_{1},\dotsc ,v_{n}\in \mathbb {R}$ als Linearkombination dieser Vektoren darstellen. Weitere Erzeugendensysteme können durch Hinzunahme zusätzlicher „überflüssiger“ Vektoren erhalten werden. Insbesondere stellt auch die Menge aller Vektoren des $\mathbb {R} ^{n}$ ein Erzeugendensystem des $\mathbb {R} ^{n}$ dar. Es gibt auch Erzeugendensysteme, die die Vektoren $e_1,\dotsc,e_n$ nicht enthalten. Beispielsweise ist

$f_{1}=(-1,1,0,\dotsc ,0),f_{2}=(0,-1,1,\dotsc ,0),\dotsc ,f_{n}=(0,0,0,\dotsc ,-1)$

ein Erzeugendensystem des $\mathbb {R} ^{n}$ , denn jeder Vektor $v=(v_{1},\dotsc ,v_{n})\in \mathbb {R} ^{n}$ lässt sich auch durch

$v=(-v_{1})f_{1}+(-v_{1}-v_{2})f_{2}+\dotsb +(-v_{1}-v_{2}-\dotsb -v_{n})f_{n}$

darstellen.

Polynomraum

Ein Beispiel eines nicht endlich erzeugten Vektorraums ist der Polynomraum $\mathbb {R} [x]$ der Polynome mit reellen Koeffizienten in einer Variablen . Ein Erzeugendensystem des $\mathbb {R} [x]$ ist die Menge der Monome

$E=\{1,x,x^{2},\dotsc ,x^{k},\dotsc \}$ .

Dies ist ein Erzeugendensystem, weil sich jedes Polynom vom Grad als

$f(x)=a_{0}+a_{1}x+a_{2}x^{2}+\dotsb +a_{n}x^{n}$ ,

also als (endliche) Linearkombination von Monomen darstellen lässt. Auch hier gibt es viele weitere Erzeugendensysteme, zum Beispiel die Legendre-Polynome oder die Tschebyschow-Polynome. Man kann aber zeigen, dass der Polynomraum kein endliches Erzeugendensystem besitzt.

Folgenraum

Ein weiteres Beispiel eines nicht endlich erzeugten Vektorraums ist der Folgenraum $\omega$ der reellen Zahlenfolgen $(a_{0},a_{1},a_{2},\dotsc )$ mit $a_{i}\in \mathbb{R}$ für $i\in \mathbb{N}$ . In diesem Fall stellt jedoch die naheliegende Wahl von

$e_{0}=(1,0,0,\dotsc ),e_{1}=(0,1,0,\dotsc ),e_{2}=(0,0,1,\dotsc ),\dotsc$

kein Erzeugendensystem von $\omega$ dar, weil sich nicht jede Folge als (endliche) Linearkombination der $e_{i}$ darstellen lässt. Dies ist lediglich für Folgen möglich, bei denen nur endlich viele Folgenglieder ungleich Null sind. Ein Erzeugendensystem von $\omega$ besteht zwangsläufig aus überabzählbar vielen Elementen.

Nullvektorraum

Der Nullvektorraum $\{0\}$ , der nur aus dem Nullvektor $0$ besteht, besitzt die beiden Erzeugendensysteme

$E=\emptyset$ und $E=\{0\}$ .

Die leere Menge bildet ein Erzeugendensystem des Nullvektorraums, da die leere Summe von Vektoren per Definition den Nullvektor ergibt.

Minimalität

Ein Erzeugendensystem $E\subseteq V$ heißt minimal, falls kein Vektor $e \in E$ existiert, sodass $E\setminus \{e\}$ weiterhin ein Erzeugendensystem von ist. Gemäß dem Basisauswahlsatz kann aus jedem nicht-minimalen Erzeugendensystem durch Weglassen „überflüssiger“ Elemente ein minimales Erzeugendensystem ausgewählt werden. Das ist leicht im Fall endlich-dimensionaler Vektorräume zu sehen, im Fall unendlich-dimensionaler Vektorräume benötigt man für den Beweis das Lemma von Zorn.

Ein minimales Erzeugendensystem besteht stets aus linear unabhängigen Vektoren. Wären nämlich die Vektoren in nicht linear unabhängig, dann gibt es einen Vektor $e \in E$ , der sich als Linearkombination von Vektoren in $E\setminus \{e\}$ darstellen lässt. Dann lässt sich aber jede Linearkombination von Vektoren aus auch als Linearkombination von Vektoren in $E\setminus \{e\}$ schreiben und wäre nicht minimal. Jedes minimale Erzeugendensystem stellt somit eine Basis des Vektorraums dar, das heißt jeder Vektor des Raums lässt sich eindeutig als Linearkombination der Basisvektoren darstellen.

Erzeugte Untervektorräume

Zu einer beliebigen Menge $E\subseteq V$ kann auch der von erzeugte Untervektorraum $W\subseteq V$ betrachtet werden. Zur Konstruktion von gibt es die folgenden beiden Verfahren.

Bei dem ersten Verfahren wird der Durchschnitt aller Untervektorräume von , die enthalten, betrachtet. Dies ist selbst ein Untervektorraum von , da der Durchschnitt einer nichtleeren Menge von Untervektorräumen wiederum ein Untervektorraum ist, und mit sich selbst zumindest einen Untervektorraum besitzt, der enthält. Dieser Untervektorraum ist der kleinste Untervektorraum im Sinne der Inklusion, der als Teilmenge enthält.

Bei dem zweiten Verfahren wird die Menge aller möglichen Linearkombinationen von Elementen der Menge betrachtet. Diese Menge wird die lineare Hülle von genannt und mit $\langle E\rangle$ bezeichnet. Der Untervektorraum ist damit genau der von im Sinne der obigen Definition erzeugte Vektorraum. Die Menge ist also ein Erzeugendensystem von .

Erzeugendensysteme in der Gruppentheorie

Definition

Ist eine Gruppe, dann heißt eine Teilmenge $E\subseteq G$ ein Erzeugendensystem von , wenn sich jedes Element $g\in G$ als endliches Produkt von Elementen aus und deren Inversen darstellen lässt. Das heißt jedes Gruppenelement hat eine Darstellung der Form

$g=a_{1}\,a_{2}\dotsm a_{n}$

mit $n \in \N_0$ und $a_{i}\in E$ oder $a_{i}^{{-1}}\in E$ für $i=1,\dotsc ,n$ . Eine solche Zerlegung ist im Allgemeinen nicht eindeutig bestimmt. Eine Gruppe heißt endlich erzeugt, wenn sie ein Erzeugendensystem aus endlich vielen Elementen besitzt.

Beispiele

Gruppe der ganzen Zahlen

Ein anschauliches Beispiel ist die Gruppe $(\Z,+)$ der ganzen Zahlen mit der Addition als Verknüpfung und dem neutralen Element $0$ . Die erlaubten Operationen sind hier die Addition von Zahlen und der Übergang zum Negativen einer Zahl. Diese Gruppe wird von der einelementigen Menge

$E=\{1\}$

erzeugt, denn jede positive Zahl lässt sich durch sukzessive Addition $1+\dotsb +1$ aus der gewinnen und alle weiteren durch $1+(-1)+\dotsb +(-1)$ . Analog ist auch

$E=\{-1\}$

ein Erzeugendensystem von $\mathbb {Z}$ . Diese beiden Erzeugendensysteme sind minimal, denn ihre einzige echte Teilmenge ist die leere Menge, und diese stellt kein Erzeugendensystem für $\mathbb {Z}$ dar. Ein weiteres Erzeugendensystem ist

$E=\{2,3\}$ ,

denn 3+(-2)=1 und durch $\{1\}$ wird bereits ganz $\mathbb {Z}$ erzeugt. Es ist sogar minimal, das heißt keine echte Teilmenge von ist ein Erzeugendensystem. Dieses Beispiel zeigt, dass minimale Erzeugendensysteme nicht unbedingt von minimaler Mächtigkeit sein müssen, denn $\{1\}$ und $\{-1\}$ sind Erzeugendensysteme von echt kleinerer Mächtigkeit. Im Allgemeinen wird $\mathbb {Z}$ von einer nicht-leeren Teilmenge $E\subseteq {\mathbb Z}$ erzeugt, wenn der größte gemeinsame Teiler aller Elemente aus den Betrag |d|=1 hat. Das zeigt der euklidische Algorithmus, denn dieser produziert als Nebenprodukt eine Darstellung von als ganze Linearkombination von Elementen aus (und jede solche Linearkombination wird von geteilt).

Zyklische Gruppen

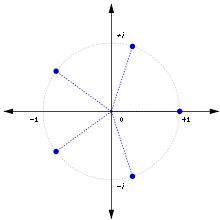
Die Gruppe der fünften Einheitswurzeln ist zyklisch, jedes von verschiedene Element ist ein Erzeuger.

Besitzt eine Gruppe ein einelementiges Erzeugendensystem

$E=\{a\}$ ,

dann nennt man die Gruppe zyklisch mit dem Erzeuger . Hier gilt dann

$G=\{a^{z}\mid z\in \mathbb {Z} \}$ ,

das heißt die Gruppe besteht aus den ganzzahligen Potenzen des Erzeugers . Damit ist auch

$E=\{a^{{-1}}\}$

ein Erzeugendensystem von . Die zyklischen Gruppen können vollständig klassifiziert werden. Zu jeder natürlichen Zahl gibt es eine zyklische Gruppe $C_{n}$ mit genau Elementen und es gibt die unendliche zyklische Gruppe $C_\infty$ . Jede andere zyklische Gruppe ist zu einer dieser Gruppen isomorph. Insbesondere ist $C_\infty$ isomorph zur obigen additiven Gruppe der ganzen Zahlen und $C_{n}$ ist isomorph zur Restklassengruppe $\Z / n \Z$ mit der Addition (modulo ) als Verknüpfung. In dieser Restklassengruppe ist jede Zahl , die teilerfremd zu ist, ein Erzeuger. Ist prim, dann stellt sogar jede Zahl $a\neq 0$ einen Erzeuger dar.

Diedergruppe

Die achtelementige Symmetriegruppe des Quadrats wird von der Drehung um 90° und der Spiegelung an einer Mittelsenkrechten erzeugt.

Ein Beispiel für eine Gruppe, die von mindestens zwei Elementen erzeugt wird, ist die Diedergruppe $D_{n}$ . Die Diedergruppe ist die Isometriegruppe eines regelmäßigen -Ecks in der Ebene. Sie besteht aus Elementen, nämlich den Drehungen $r_{0},\dotsc ,r_{n-1}$ und den Spiegelungen $s_{0},\dotsc ,s_{n-1}$ . Die Drehung $r_{k}$ dreht das Polygon dabei um den Winkel $2\pi k/n$ und die Spiegelung s_k spiegelt es an einer Achse, die im Winkel $\pi k/n$ geneigt ist. Ein Erzeugendensystem der Diedergruppe ist

$E=\{r_{1},s_{0}\}$ ,

denn jede Drehung kann durch wiederholte Anwendung von $r_{1}$ dargestellt werden (die Drehungen bilden eine zyklische Untergruppe), das heißt r_k = r_1^k , und jede Spiegelung durch Anwendung von $s_{0}$ und einer nachfolgenden Drehung, also $s_{k}=r_{1}^{k}\,s_{0}$ . Die Spiegelung $s_{0}$ kann dabei auch durch eine beliebige andere Spiegelung s_k ersetzt werden. Die Diedergruppe besitzt auch das Erzeugendensystem

$E=\{s_{0},s_{1}\}$

bestehend aus zwei Spiegelungen, denn die Drehung $r_{1}$ hat die Darstellung $r_{1}=s_{1}\,s_{0}$ und $\{r_{1},s_{0}\}$ wurde bereits als Erzeugendensystem identifiziert. Statt $s_{0},s_{1}$ bilden auch zwei beliebige benachbarte Spiegelungen $s_{k},s_{{k+1}}$ ein Erzeugendensystem der Diedergruppe, denn es gilt auch $r_{1}=s_{{k+1}}\,s_{k}$ .

Gruppen rationaler Zahlen

Ein Beispiel für eine nicht endlich erzeugte Gruppe ist die Gruppe $(\Q, +)$ der rationalen Zahlen mit der Addition als Verknüpfung. Diese Gruppe wird beispielsweise von der Menge der Stammbrüche

$E=\left\{{\tfrac {1}{1}},{\tfrac {1}{2}},{\tfrac {1}{3}},\dotsc \right\}$

erzeugt. Sie lässt sich jedoch von keiner endlichen Menge $\{q_{1},\dotsc ,q_{n}\}$ rationaler Zahlen erzeugen. Zu jeder solchen Menge lässt sich nämlich eine weitere rationale Zahl finden, die sich nicht als Summe der Zahlen $q_{1},\dotsc ,q_{n}$ und ihrer Gegenzahlen darstellen lässt. Hierzu wird einfach der Nenner der Zahl teilerfremd zu den Nennern der Zahlen $q_{1},\dotsc ,q_{n}$ gewählt. Auch die Gruppe $(\mathbb {Q} ^{+},\cdot )$ der positiven rationalen Zahlen mit der Multiplikation als Verknüpfung ist nicht endlich erzeugt. Ein Erzeugendensystem dieser Gruppe ist die Menge der Primzahlen

$E=\{2,3,5,\dotsc \}$ .

Triviale Gruppe

Die triviale Gruppe $\{e\}$ , die nur aus dem neutralen Element besteht, besitzt die beiden Erzeugendensysteme

$E=\emptyset$ und $E=\{e\}$ .

Die leere Menge bildet ein Erzeugendensystem der trivialen Gruppe, da das leere Produkt von Gruppenelementen per Definition das neutrale Element ergibt.

Symmetrie

Der Cayleygraph der freien Gruppe mit zwei Erzeugern a und b

Ein Erzeugendensystem heißt symmetrisch, wenn

$a\in E\Longleftrightarrow a^{{-1}}\in E$

gilt. Jedem endlichen, symmetrischen Erzeugendensystem einer Gruppe kann man seinen Cayley-Graphen zuordnen. Unterschiedliche endliche, symmetrische Erzeugendensysteme derselben Gruppe geben quasi-isometrische Cayley-Graphen, der Quasi-Isometrie-Typ des Cayley-Graphen ist also eine Invariante endlich erzeugter Gruppen.

Präsentation von Gruppen

→ Hauptartikel: Präsentation einer Gruppe

Allgemein kann eine Gruppe als Bild unter der kanonischen Abbildung $h\colon F(E)\to G$ der freien Gruppe F(E) über dem Erzeugendensystem dargestellt werden, wobei die Inklusion $f\colon E\to G$ fortsetzt. Dies erklärt die obige explizite Beschreibung des Erzeugnisses. Weiterhin findet diese Interpretation wichtige Anwendungen in der Gruppentheorie. Wir nehmen an, dass surjektiv ist, das heißt dass von erzeugt wird. Die Kenntnis des Kernes von bestimmt dann bis auf Isomorphie eindeutig. In günstigen Fällen lässt sich der Kern selbst wiederum durch Erzeuger $M\subseteq N$ einfach beschreiben. Das Datum (E,M) legt dann bis auf Isomorphie eindeutig fest.

Erzeugte Untergruppen

Die von einer beliebigen Menge $E\subseteq G$ erzeugte Untergruppe von wird mit $\langle E\rangle$ bezeichnet, sie besteht aus dem neutralen Element und allen endlichen Produkten $a_{1}\,a_{2}\dotsm a_{n}$ , für die für $1\leq i\leq n$ jeweils $a_{i}\in E$ oder $a_{i}^{{-1}}\in E$ ist. Damit ist

$\{a\in E\}\cup \left\{a:a^{-1}\in E\right\}$

ein symmetrisches Erzeugendensystem von $\langle E\rangle$ .

Topologische Gruppen

In der Theorie der topologischen Gruppen interessiert man sich in der Regel für abgeschlossene Untergruppen und vereinbart daher, unter dem Erzeugnis einer Teilmenge die kleinste abgeschlossene Untergruppe, die enthält, zu verstehen.

Da die Verknüpfung und die Inversenbildung stetig sind, ist der Abschluss $\overline {\langle E\rangle }$ des algebraischen Erzeugnisses $\langle E\rangle$ wieder eine Untergruppe von . Daher ist das Erzeugnis einer Teilmenge $E\subseteq G$ einer topologischen Gruppe der Abschluss des Gruppenerzeugnisses $\langle E\rangle$ .

Besitzt als topologische Gruppe ein endliches Erzeugendensystem, so wird auch als topologisch endlich erzeugt bezeichnet.

Da $\mathbb {Z}$ in den ganzen p-adischen Zahlen $\mathbb {Z} _{p}$ dicht ist, wird $\mathbb {Z} _{p}$ als topologische Gruppe von erzeugt. Es ist also topologisch endlich erzeugt. Aus der Terminologie der proendlichen Gruppen leitet sich ab, dass $\mathbb {Z} _{p}$ prozyklisch ist.

Erzeugendensysteme in der Algebra

Ringe

Sei ein kommutativer Ring mit Eins. Ein Erzeugendensystem eines Ideals $I\subset R$ ist eine Menge $J\subset I$ mit der Eigenschaft, dass sich jedes $a\in I$ als

$a=r_{1}a_{1}+\dotsb +r_{n}a_{n}$

mit $n \in \N_0$ , $r_{1},\dotsc ,r_{n}\in R$ und $a_{1},\dotsc ,a_{n}\in J$ zerlegen lässt. Ein Ideal $I\subset R$ heißt endlich erzeugt, wenn es eine endliche Teilmenge $\left\{a_{1},\dotsc ,a_{n}\right\}\subset I$ mit $I=Ra_{1}+\dotsb +Ra_{n}$ gibt. Ein Hauptideal ist ein von einer einelementigen Menge erzeugtes Ideal. Insbesondere ist der Ring ein Hauptideal, denn er wird von $\{1\}$ erzeugt. Ein Ring ist noethersch genau dann, wenn alle Ideale endlich erzeugt sind.

Moduln

Eine Teilmenge $E\subseteq M$ eines (linken) -Moduls ist ein Erzeugendensystem, wenn sich jedes $x\in M$ als endliche Summe

$x=r_{1}e_{1}+\dotsb +r_{n}e_{n}$

mit $n \in \N_0$ , $r_{1},\dotsc ,r_{n}\in R$ und $e_{1},\dotsc ,e_{n}\in E$ darstellen lässt. Eine analoge Definition gilt für rechte -Moduln. Ein -Modul heißt frei, wenn er ein Erzeugendensystem bestehend aus linear unabhängigen Elementen besitzt.

Erzeugendensysteme in Maßtheorie und Topologie

σ-Algebren

In der Maß- und Integrationstheorie untersucht man sogenannte σ-Algebren. Für eine Grundmenge und eine beliebige Teilmenge ${\mathcal {E}}\subseteq \operatorname {Pot}(X)$ der Potenzmenge von bezeichnet $\sigma ({\mathcal {E}})$ die von ${\mathcal {E}}$ erzeugte σ-Algebra, also die kleinste σ-Algebra auf , die alle Mengen aus ${\mathcal {E}}$ enthält. Sie wird konstruiert als der Durchschnitt aller ${\mathcal {E}}$ enthaltenden σ-Algebren auf , da es im Allgemeinen schwierig ist, das Erzeugnis als solches explizit anzugeben. Man betrachtet zum Beispiel einen topologischen Raum $(X,{\mathcal {T}})$ und sucht in diesem eine kleinste σ-Algebra auf , die alle offenen Mengen enthält, also die von ${\mathcal {T}}$ erzeugte σ-Algebra $\sigma ({\mathcal {T}})$ . Die dadurch eindeutig bestimmte σ-Algebra heißt die Borelsche σ-Algebra. Diese ist in der Integrationstheorie von zentraler Bedeutung.

Topologien

In der Topologie ist der Begriff des Erzeugendensystems mit dem der Subbasis gleichbedeutend. Hierbei handelt es sich um ein Mengensystem ${\mathcal {E}}\subseteq {\mathcal {T}}$ offener Teilmengen eines topologischen Raumes $(X,{\mathcal {T}})$ , welches die Topologie ${\mathcal {T}}$ erzeugt. Dies bedeutet, dass aus den in ${\mathcal {T}}$ enthaltenen Elementen allein durch die beiden Operationen der Bildung des Durchschnitts endlich vieler Mengen und der Bildung der Vereinigungsmenge beliebig vieler Mengen jede offene Menge $O\subseteq X$ erzeugt wird.

${\mathcal {E}}\subseteq {\mathcal {T}}$ ist also dadurch gekennzeichnet, dass ${\mathcal {T}}$ die gröbste Topologie auf der Grundmenge ist, bezüglich welcher die Mengen in ${\mathcal {E}}$ alle offen sind. Mithin ist ${\mathcal {T}}$ der Durchschnitt aller Topologien auf , welche ${\mathcal {E}}$ enthalten.

Kann sogar die Topologie ${\mathcal {T}}$ aus ${\mathcal {E}}$ allein durch Bildung beliebiger Vereinigungsmengen erzeugt werden, so nennt man ${\mathcal {E}}$ eine Basis der Topologie ${\mathcal {T}}.$

Mengentheoretische Formulierung

Es sei eine Grundmenge und ein System ${\mathfrak {B}}\subseteq {\mathcal {P}}(X)$ von Teilmengen von gegeben. Diese Teilmengen entsprechen dabei den Unterstrukturen von , die im Folgenden betrachtet werden. Sei weiter eine Menge $E\subseteq X$ gegeben. Dann wird nach der kleinsten Menge $A\in {\mathfrak {B}}$ gefragt, so dass $E\subseteq A$ gilt. Die Menge ist dann der Erzeuger von . Ein solches Element existiert und ist eindeutig bestimmt, sofern gilt

${\mathfrak {B}}$ ist stabil unter beliebigen Durchschnitten, das heißt ist $S\subseteq {\mathfrak {B}}$ eine nichtleere Teilmenge, so ist auch der Durchschnitt $\textstyle \bigcap S\in {\mathfrak {B}}$ .
Es gibt mindestens ein Element aus ${\mathfrak {B}}$ mit der Eigenschaft $E\subseteq A$ (meist gilt $X\in {\mathfrak B}$ ).

Das Erzeugnis hat dann die Darstellung

$A=\bigcap \{B\in {\mathfrak {B}}\mid E\subseteq B\}$ .

Dies trifft auf alle obigen Beispiele zu. Im Fall von Vektorräumen ist das betrachtete Mengensystem ${\mathfrak {B}}$ die Menge der Untervektorräume eines Vektorraums und die Grundmenge ist X=V . Im Fall von Gruppen ist ${\mathfrak {B}}$ die Menge der Untergruppen einer Gruppe und die Grundmenge ist X=G . Im Fall der σ-Algebren ist ${\mathfrak {B}}$ die Menge der σ-Algebren auf ${\mathcal {T}}$ und die Grundmenge $X={\mathcal {P}}({\mathcal {T}})$ . Dies gilt mutatis mutandis auch für alle anderen genannten Beispiele.

Siehe auch

Hüllenoperator

Basierend auf einem Artikel in:

Wikipedia.de