
Torus

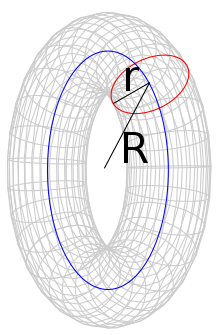
Ein Torus (Plural Tori, von lateinisch torus) ist ein mathematisches Objekt aus der Geometrie und der Topologie. Er ist eine wulstartig geformte Fläche mit einem Loch, hat also die Gestalt eines Tennisrings, auch Rettungsrings, Reifens oder Donuts.
Beispiele für im dreidimensionalen Raum eingebettete Tori sind die Rotationstori. Rotationstori sind Rotationsflächen, die man erhält, indem man einen Kreis um eine Achse rotieren lässt, die in der Kreisebene liegt und den Kreis nicht schneidet. Falls man nicht nur die Kreislinie, sondern die gesamte Kreisfläche rotieren lässt, erhält man einen Volltorus.
Anders ausgedrückt wird ein Rotationstorus aus derjenigen Menge an Punkten gebildet, die
von einer Kreislinie mit Radius
den festen Abstand
mit
haben.

Ein Torus kann auch durch Identifizieren der Seiten eines Parallelogramms konstruiert werden. Dabei wird die rechte Kante des Parallelogramms mit seiner linken Kante und die obere mit der unteren Kante verheftet. Diese Topologie benutzen auch viele Computerspiele: Verlässt ein Spielobjekt auf einer Seite das Spielfeld, so taucht es auf der gegenüberliegenden Seite wieder auf.
Beide Konstruktionen sind Spezialfälle der allgemeinen mathematischen Definition, die einen Torus als das topologische Produkt zweier Kreise definiert. Dieser Begriff spielt in zahlreichen Gebieten der Mathematik eine Rolle, neben Topologie und Differentialgeometrie ist er unter anderem in der Fourier-Analysis, der Theorie dynamischer Systeme (invariante Tori in der Himmelsmechanik), der Funktionentheorie und der Theorie elliptischer Kurven von Bedeutung.
Rotationstori liefern eine konkrete rotationssymmetrische Realisierung dieser Fläche im dreidimensionalen euklidischen Raum. Für viele Anwendungen in theoretischer Mathematik und Physik bedeutend ist eine andere Einbettung als flacher Torus in den vierdimensionalen Raum. Diese hat die Krümmung null und die maximal mögliche Symmetrie.
Der Torus ist eine zweidimensionale
Fläche.
Allgemeiner betrachtet man in der Mathematik
auch den -Torus,
eine den zweidimensionalen Torus verallgemeinernde
-dimensionale
Mannigfaltigkeit.
Davon abweichend finden sich in der deutschsprachigen Literatur gelegentlich
auch die Bezeichnungen Doppeltorus, Tripeltorus etc. für Flächen mit zwei, drei
und mehr Löchern.
Volumen
Das Volumen des Torus lässt sich als Volumenintegral über die Jacobi-Determinante (die Determinante der Funktionalmatrix) berechnen. Die Jacobi-Matrix zur Parametrisierung des Torus lässt sich wie folgt angeben:
Daraus folgt:
Die Funktionaldeterminante ist hier also gleich der Norm des Flächennormalenvektors.
Man erhält also für das Volumen des Volltorus .
Die Formel
für das Volumen lässt sich so
interpretieren, dass die Kreisfläche
mit dem Umfang
multipliziert
wird (siehe Zweite
Guldinsche Regel). Dies kann man zum Verständnis in Analogie zum Zylindervolumen
setzen. Mit dem Flächeninhalt
der Oberfläche verhält es sich genauso, hier werden die Umfänge
und
miteinander multipliziert (siehe Erste
Guldinsche Regel). Dies steht ebenfalls in Analogie zur Zylinderoberfläche
.
Betrachtet man nur den inneren Teil des Torus, der von der -Achse
einen Abstand kleiner gleich
hat, ergibt sich das Volumen
Der äußere Teil des Torus, der von der -Achse
einen Abstand größer gleich
hat, hat das Volumen
Oberfläche
Die Oberfläche des Torus mit der obigen Parameterdarstellung ist
Diese Formel lässt sich entweder mit der Ersten Guldinschen Regel herleiten aus
oder mit Hilfe des Oberflächenintegrals
berechnen. Dabei ist
das Oberflächenelement
des Torus in der obigen Parameterdarstellung.
Der Torus berandet
einen 3-dimensionalen Volltorus.
Das Volumen
des Volltorus beträgt
(siehe Zweiten
Guldinschen Regel).
Betrachtet man nur den inneren Teil des Torus, der von der -Achse
einen Abstand kleiner gleich
hat, ergibt sich die Oberfläche
Der äußere Teil des Torus, der von der -Achse
einen Abstand größer gleich
hat, hat die Oberfläche
Torus als Rotationsfläche
Ein Rotationstorus ist eine Rotationsfläche,
die durch Rotation eines Kreises um eine in der Kreisebene
liegende und den Kreis nicht schneidende Rotationsachse
erzeugt wird.
Ein Rotationstorus kann als Menge
der Punkte
beschrieben werden, die von einer Kreislinie mit Radius
den festen Abstand
haben, wobei
ist. In kartesischen Koordinaten
,
mit der z-Achse als Rotationsachse und den Mittelpunkten
des rotierenden Kreises in der x-y-Ebene wird er durch die Gleichung
beschrieben. Durch Beseitigen der Wurzel ergibt sich die Gleichung 4. Grades
Man kann in der Torusoberfläche eine toroidale Koordinate
und eine dazu senkrechte poloidale Koordinate
einführen. Man denkt sich den Torus als durch einen Kreis
entstanden, der um eine in der Kreisebene liegende Achse rotiert wird. Den
Radius des ursprünglichen Kreises nennen wir
,
dieser Kreis bildet auch gleichzeitig eine Koordinatenlinie von
.
Den Abstand des Kreismittelpunkts
von der Achse nennen wir
,
die Koordinatenlinien
von
sind Kreise um die Drehachse.
Beide Koordinaten sind Winkel und laufen von
bis
.
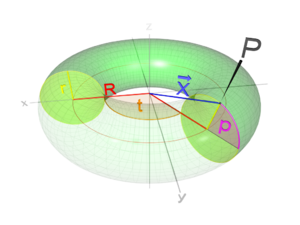


Parametrisierung
Die Umrechnung von Toruskoordinaten in kartesische Koordinaten ist
Toruskoordinaten sind in der Kernfusionstechnologie von Bedeutung.
Ebene Schnitte
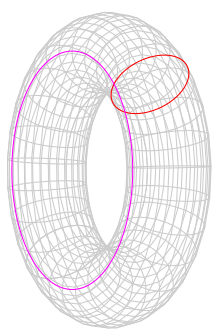
- Schnitte mit Ebenen, die die Rotationsachse enthalten, sind Kreispaare.
- Schnitte mit Ebenen, die zur Rotationsachse senkrecht sind, sind Kreispaare oder ein Kreis oder leer.
- Eine zur Rotationsachse parallele Ebene schneidet aus einem Torus eine spirische Kurve aus. In Sonderfällen kann dies eine Cassinische Kurve sein.
- Eine geneigte Ebene, die zwei Erzeugerkreise berührt, schneidet Villarceau-Kreise aus.
Tori in der Darstellenden Geometrie
In der Darstellenden Geometrie verwendet man Teile eines Torus zur Konstruktion von Übergangsflächen zwischen Zylindern. Die Darstellung eines Torus durch seinen Umriss findet man in Umrisskonstruktionen.
Allgemeine Definition
Mit
werde der Kreis
(die 1-Sphäre)
bezeichnet. Der
-Torus
ist dann definiert durch
,
wobei
das Produkt
topologischer Räume ist. Die im vorhergehenden Abschnitt beschriebene Rotationsfläche
ist ein 2-Torus. Der 2-Torus wird meist einfach Torus genannt.
Topologische Eigenschaften
Struktur einer Mannigfaltigkeit
Der -Torus
ist eine topologische
Mannigfaltigkeit. Dies folgt aus der Tatsache, dass der
-Torus
das topologische
Produkt aus
1-Sphären
ist und die 1-Sphäre selbst eine topologische Mannigfaltigkeit ist. Die 1-Sphäre
ist zusätzlich auch eine differenzierbare
Mannigfaltigkeit und, da das Produkt
differenzierbarer Mannigfaltigkeiten wieder eine differenzierbare
Mannigfaltigkeit ergibt, ist der
-Torus
ebenfalls eine differenzierbare Mannigfaltigkeit. Die Dimension
von
ist gleich
.
Topologische Eigenschaften
Ebenfalls direkt aus der Definition folgt, dass der -Torus
kompakt ist. Außerdem
ist er wegzusammenhängend.
Im Gegensatz zur
-Sphäre
ist der
-Torus
für
nicht einfach
zusammenhängend.
Die Abbildung
,
definiert durch
,
ist die universelle
Überlagerung des
-Torus.
Lie-Gruppe
Die 1-Sphäre,
aufgefasst als Kreisgruppe,
ist außerdem eine Lie-Gruppe.
Da das Produkt
mehrerer Lie-Gruppen mit der komponentenweisen Multiplikation
wieder eine Lie-Gruppe ist, ist auch der -Torus
eine Lie-Gruppe.
Eingebettete Tori
Flache Tori
Da die Kreislinie
offensichtlich in den
eingebettet
werden kann, kann der
-Torus
als Teilmenge des euklidischen Raums
aufgefasst werden. Man betrachtet auf
die riemannsche
Metrik
,
die durch die euklidische
Metrik des Raums
auf dem
-Torus
induziert wird. Diese Metrik
ist flach,
das heißt, der
-Torus
ist lokal isometrisch
zu einer Umgebung
des
.
Insbesondere ist daher seine Schnittkrümmung
überall konstant null. Da der
-Torus
kompakt und somit auch vollständig
ist, ist er eine flache
Mannigfaltigkeit. Man spricht daher auch von einem flachen
-Torus.
Es gibt neben der oben beschriebenen noch weitere flache Metriken auf dem
Torus. Flache 2-Tori können beschrieben werden durch ein Parallelogramm, dessen
gegenüberliegende Seiten zusammengeklebt werden. Äquivalent dazu können flache
Tori als topologische Faktorgruppen
für zwei linear
unabhängige Vektoren
beschrieben werden. Im Spezialfall
und
erhält man den Quotienten
.
Elliptische
Kurven über den komplexen
Zahlen lassen sich mittels der Weierstraßschen Parametrisierung als
für ein Gitter
darstellen und sind dadurch (mit einer translationsinvarianten
Metrik)
Beispiele für flache Tori. Der Modulraum
der elliptischen
Kurven oder äquivalent der flachen 2-Tori ist die sogenannte Modulkurve.
Flache Tori im dreidimensionalen Raum
Eine 2-mal differenzierbare Einbettung des Torus in den dreidimensionalen Raum kann nicht flach sein, weil die lokalen Extrema Punkte positiver Krümmung sein müssen. Nach dem Einbettungssatz von Nash gibt es jedoch fraktale (nur 1-mal differenzierbare) Einbettungen des flachen Torus in den dreidimensionalen Raum. Diese können auch numerisch konstruiert werden.
Rotationstori im dreidimensionalen Raum
Ein Rotationstorus ist ein im
eingebetteter 2-Torus, der als Menge
der Punkte
beschrieben werden kann, die von einer Kreislinie mit Radius
den festen Abstand
haben, wobei
ist.
Clifford-Tori
Ein Clifford-Torus ist ein spezieller in
eingebetter Torus. Nach der Identifizierung
und
lässt sich der Standard-Cliffordtorus beschreiben als
.
Weiterhin werden die Bilder von
unter Isometrien der Standard-Metrik
als Clifford-Tori bezeichnet.
Mittels stereographischer
Projektion kann man Clifford-Tori auch als in den
eingebettete Tori auffassen.
Ein Clifford-Torus ist eine Minimalfläche
bzgl. der Standardmetrik
auf der .
Die von Brendle
bewiesene Lawson-Vermutung besagt, dass jeder als Minimalfläche in die
eingebettete Torus ein Clifford-Torus ist.
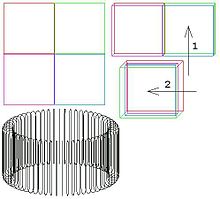
Konstruktion aus einem Quadrat oder Würfel
Konstruktion zweidimensionaler Tori aus einem Quadrat oder Parallelogramm
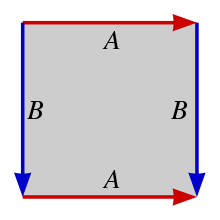
Im Gegensatz zur Oberfläche einer Kugel kann der Torus ohne Singularitäten auf einer ebenen, rechteckigen Fläche abgebildet werden.
Dabei wird die rechte Kante des Rechtecks oder Quadrats mit seiner linken Kante verheftet und seine untere Kante wird mit seiner oberen Kante verheftet. Diese Konstruktion funktioniert auch mit einem beliebigen Parallelogramm. Diese Topologie besitzen auch viele Computerspiele, zum Beispiel Asteroids oder Pac-Man: Verlässt ein Spielobjekt auf einer Seite das Spielfeld, so taucht es auf der gegenüberliegenden Seite wieder auf.
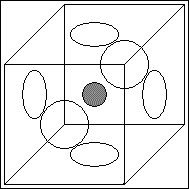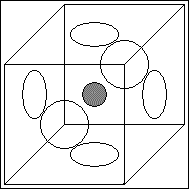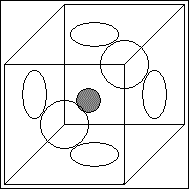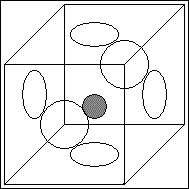
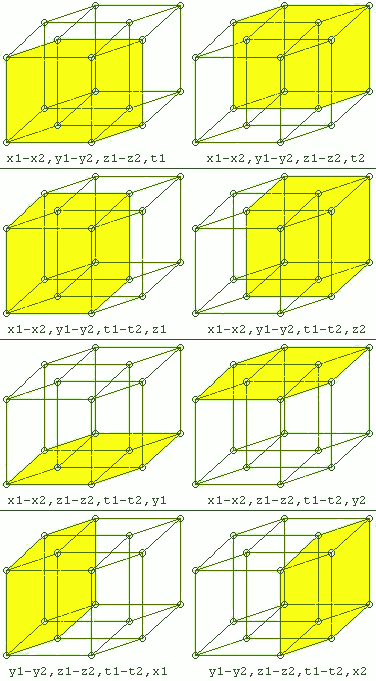
Konstruktion höherdimensionaler Tori aus einem Würfel oder Parallelepiped
Beim dreidimensionalen Torus oder 3-Torus handelt es sich um einen Quader oder Würfel, dessen sechs gegenüberliegende Flächen paarweise miteinander verheftet sind.
Beim vierdimensionalen Torus oder 4-Torus handelt es sich um einen Tesserakt, dessen acht gegenüberliegende Würfel paarweise miteinander verheftet sind.
Allgemein ist der -dimensionale
Torus ein
-dimensionaler
Würfel
,
dessen gegenüberliegende
-Hyperwürfel paarweise
miteinander identifiziert sind. Man kann ihn auch als
darstellen.
Auch hier kann man statt eines -dimensionalen
Würfels
ein beliebiges
-dimensionales
Parallelepiped
verwenden, um durch Identifizieren der Seiten einen
-dimensionalen
Torus zu konstruieren.
Sieben-Farben-Satz
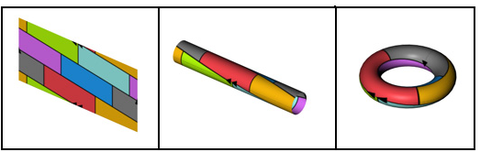

Der Sieben-Farben-Satz für den Torus besagt, dass 7 Farben immer ausreichen, eine beliebige Landkarte auf der Oberfläche eines Torus so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen.
Das bedeutet, dass jeder Graph,
der in den Torus eingebettet werden kann, eine chromatische Zahl von höchstens 7
hat (siehe Knotenfärbung).
Weil der vollständige
Graph
in den Torus eingebettet werden kann, ist die chromatische Zahl gleich 7.
In der Ebene oder auf einer Kugeloberfläche reichen weniger Farben. Der Vier-Farben-Satz besagt, dass vier Farben immer ausreichen, eine beliebige Landkarte in der euklidischen Ebene so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen.
Algebraischer Torus
In der Theorie algebraischer Gruppen wird Torus in einem anderen Sinn verwendet. Dort ist damit eine Gruppe gemeint, die isomorph zu einem endlichen Produkt von Kopien der multiplikativen Gruppe eines Körpers ist. Zur Abgrenzung spricht man dann von einem algebraischen Torus im Gegensatz zu einem topologischen Torus.
So ist zum Beispiel in der torischen Geometrie, dem Studium torischer Varietäten, ein Torus üblicherweise ein algebraischer Torus.
Anwendungsbeispiele

Ein Rettungsring mit dem Außendurchmesser
76 Zentimeter
und dem Innendurchmesser
44 Zentimeter hat die Form eines Torus. Er hat also den festen Abstand
von einer Kreislinie mit dem Radius
.
Daraus ergeben sich das Volumen und die Oberfläche:
- Volumen:
- Oberfläche:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.12. 2025