
Dynamisches System
Ein (deterministisches) dynamisches System ist ein mathematisches Modell eines zeitabhängigen Prozesses, der homogen bezüglich der Zeit ist, also dessen weiterer Verlauf nur vom Anfangszustand, aber nicht von der Wahl des Anfangszeitpunkts abhängt. Der Begriff des dynamischen Systems geht in seiner heutigen Form auf die Mathematiker Henri Poincaré und George David Birkhoff zurück.
Dynamische Systeme finden vielfältige Anwendungen auf Prozesse im Alltag und erlauben Einblicke in viele Bereiche nicht nur der Mathematik (z.B. Zahlentheorie, Stochastik), sondern auch der Physik (z.B. Pendelbewegung, Klimamodelle) oder der theoretischen Biologie (z.B. Räuber-Beute-Modelle).
Man unterscheidet zwischen diskreter und kontinuierlicher Zeitentwicklung. Bei einem zeitdiskreten dynamischen System ändern sich die Zustände in äquidistanten Zeitsprüngen, d.h. in aufeinanderfolgenden, stets gleich großen zeitlichen Abständen, während die Zustandsänderungen eines zeitkontinuierlichen dynamischen Systems in infinitesimal kleinen Zeitschritten stattfinden. Das wichtigste Beschreibungsmittel für zeitkontinuierliche dynamische Systeme sind autonome gewöhnliche Differenzialgleichungen. Ein gemischtes System aus kontinuierlichen und diskreten Teilsystemen mit kontinuierlich-diskreter Dynamik wird auch als hybrid bezeichnet. Beispiele solcher hybrider Dynamiken finden sich in der Verfahrenstechnik (z.B. Dosiervorlage-Systeme).
Wichtige Fragestellungen im Zusammenhang mit dynamischen Systemen betreffen vor allem ihr Langzeitverhalten (zum Beispiel Stabilität, Periodizität, Chaos und Ergodizität), die Systemidentifikation und ihre Regelung.
Einführende Beispiele
Exponentielles Wachstum

Ein einfaches Beispiel für ein dynamisches System ist die zeitliche
Entwicklung einer Größe,
die einem exponentiellen
Wachstum unterliegt, wie etwa eine Population
einer ungehindert wachsenden Bakterienkultur.
Der Zustand zu einem festen Zeitpunkt ist hier durch eine nichtnegative reelle
Zahl, nämlich die Bestandsgröße der Population, gegeben, das heißt, der
Zustandsraum des Systems ist die Menge
der nichtnegativen reellen Zahlen. Betrachtet man zunächst die Zustände
zu den diskreten Zeitpunkten
,
also auf dem Zeitraum
,
dann gilt
mit einem konstanten Wachstumsfaktor
.
Für den Zustand zu einem Zeitpunkt
ergibt sich daraus
.
Die charakterisierende Eigenschaft eines dynamischen Systems ist, dass der
Zustand zwar von der verstrichenen Zeit
und vom Anfangswert
abhängt, jedoch nicht von der Wahl der Anfangszeitpunkts. Sei etwa
eine weitere exponentiell wachsende Population mit dem gleichen Wachstumsfaktor
,
aber mit dem Anfangswert
gegeben. Zu einem Zeitpunkt
gilt dann
.
Die zweite Population wächst also im Zeitabschnitt
genauso wie die erste im Zeitabschnitt
.
Dieses Verhalten lässt sich noch anders ausdrücken: Die sogenannte
Flussfunktion
,
die jedem Zeitpunkt
und jedem Anfangszustand
den Zustand
zum Zeitpunkt
zuordnet, hier also
,
erfüllt für alle
und alle
die Gleichung
.
Das ist die sogenannte Halbgruppeneigenschaft des Flusses eines dynamischen Systems.
Federpendel
Eine weitere Quelle für dynamische Systeme ist die mathematische Modellierung
mechanischer Systeme, im
einfachsten Fall die Bewegung eines Massepunktes
unter dem Einfluss einer Kraft,
die vom Ort und von der Geschwindigkeit abhängt, aber nicht explizit von der
Zeit. Der Zustand eines solchen Systems zu einem Zeitpunkt
ist gegeben als das geordnete
Paar
,
bestehend aus dem Ort
und der Geschwindigkeit
.
Insbesondere ist dann der gesamte Bewegungsablauf durch die Vorgabe einer
Anfangsposition
zusammen mit einer Anfangsgeschwindigkeit
eindeutig bestimmt. Im Fall einer eindimensionalen Bewegung ist somit der
Zustandsraum
.
 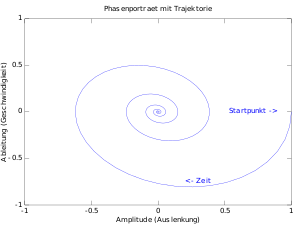 |
| Gedämpfte Schwingung und Bahn im Zustandsraum |
Als konkretes Beispiel soll ein Federpendel
betrachtet werden, auf dessen Massestück mit der Masse
die Rückstellkraft der Feder sowie möglicherweise eine geschwindigkeitsabhängige
Reibungskraft
einwirkt. Bezeichnet man die Gesamtkraft mit
,
so ergibt sich für den Zustand das gewöhnliche
Differentialgleichungssystem
wobei der Punkt über den Variablen die Ableitung nach der Zeit bezeichnet. Die erste Gleichung besagt, dass die Geschwindigkeit die Ableitung des Ortes nach der Zeit ist, und die zweite ergibt sich direkt aus dem zweiten newtonschen Axiom, nach dem Masse mal Beschleunigung gleich der auf den Massepunkt wirkenden Gesamtkraft ist.
Es lässt sich zeigen, dass auch bei diesem System der Fluss
die Halbgruppeneigenschaft erfüllt. Betrachtet man den Verlauf des
Systemzustandes im Zustandsraum ,
also die sogenannte Bahn
,
so ergibt sich bei einer gedämpften
Schwingung des Federpendels eine Trajektorie,
die spiralförmig auf die Ruhelage
zuläuft.
Definitionen
Ein dynamisches System ist ein Tripel
bestehend aus einer Menge
oder
dem Zeitraum, einer nichtleeren Menge
,
dem Zustandsraum
(dem Phasenraum),
und einer Operation
von
auf
so dass für alle Zustände
und alle Zeitpunkte
gilt:
(Identitätseigenschaft) und
(Halbgruppeneigenschaft).
Wenn
oder
ist, dann heißt
zeitdiskret oder kurz diskret, und mit
oder
nennt man
zeitkontinuierlich oder kontinuierlich.
wird außerdem als diskretes oder kontinuierliches dynamisches System für
reelle Zeit oder als invertierbar bezeichnet, falls
bzw.
gilt.
Für jedes
heißt die Abbildung
die Bewegung von
und die Menge
wird die Bahn (der (volle) Orbit, die Trajektorie, die
Phasenkurve, die Bahnkurve, die Lösungskurve) von
genannt. Der positive Halborbit oder Vorwärtsorbit von
ist
und falls
invertierbar ist, ist
der negative Halborbit oder Rückwärtsorbit von
.
Ein diskretes dynamisches System
ist stetig, wenn sein Zustandsraum
ein (nichtleerer) metrischer
Raum ist und wenn jede zu einem Zeitpunkt
gehörende Transformation
stetig
ist. Man nennt ein kontinuierliches dynamisches System
stetig oder einen Halbfluss,
wenn sein Zustandsraum
ein metrischer Raum ist und wenn jede zu einem Zeitpunkt gehörende
Transformation sowie jede Bewegung eines Zustands stetig ist. Außerdem nennt man
ein stetiges diskretes dynamisches System
auch eine Kaskade und einen Halbfluss
einen Fluss.
Der Zustandsraum eines stetigen dynamischen Systems wird auch als Phasenraum und von jedem
der Orbit als die Phasenkurve oder Trajektorie
von
bezeichnet, die einfach
geschrieben wird mit
.
Koppelt man kontinuierliche und gegebenen Falles noch zusätzliche diskrete dynamische Systeme zu einem System zusammen, so nennt man dieses ein kontinuierlich-diskretes oder auch hybrides dynamisches System.
Bemerkungen
- In der Literatur wird häufig nicht zwischen dynamischen Systemen und stetigen dynamischen Systemen bzw. Flüssen unterschieden, außerdem versteht man unter einem Fluss nicht selten einen differenzierbaren Fluss (siehe unten). Es finden sich auch allgemeinere Definitionen stetiger dynamischer Systeme, bei denen z.B. als Phasenraum eine topologische Mannigfaltigkeit, ein (u.U. kompakter) Hausdorff-Raum oder gar nur ein topologischer Raum genommen wird.
- An Stelle der Linksoperation
wie in der obigen Definition werden oft dynamische Systeme mit einer Rechtsoperation
auf
definiert, die Reihenfolge der Argumente dreht sich dann entsprechend um.
- In der Definition wird die Identitätseigenschaft von der Operation
deshalb gefordert, weil jeder Zustand
, so lang keine Zeit vergeht (also für
), sich nicht verändern soll. Diese Eigenschaft bedeutet, dass die zu
gehörende Transformation die identische Abbildung auf
ist:
- Die Halbgruppeneigenschaft macht das dynamische System bezüglich der Zeit
homogen: Man gelangt zunächst in
Zeiteinheiten vom Zustand
zum Zustand
und anschließend von dort in
Zeiteinheiten zum Zustand
, d.h. zum gleichen Zustand zu dem man direkt vom Zustand
in
Zeiteinheiten kommt. Die zu allen Zeitpunkten
gehörenden Transformationen
bilden eine kommutative Halbgruppe mit der Komposition
als Verknüpfung und mit einem neutralen Element
, außerdem ist die Abbildung
ein Halbgruppenhomomorphismus:
für alle
Diese Transformationshalbgruppe ist bei invertierbaren dynamischen Systemen sogar eine Gruppe, denn für alle
ist
das inverse Element zu
- Ein dynamisches System
mit
oder mit
lässt sich genau dann zu einem invertierbaren dynamischen System
mit
fortsetzen, wenn die zu
gehörende Transformation
eine Umkehrfunktion
besitzt. Es sind dann
und rekursiv
für alle
Ist
kontinuierlich, so sind durch
für alle
mit
und
ebenso sämtliche zu negativen Zeiten gehörenden Transformationen eindeutig gegeben. Mit
ist so genau eine Operation
von
erklärt, so dass
die invertierbare Fortsetzung von
ist.
- Wegen der Halbgruppeneigenschaft lässt sich jedes diskrete dynamische
System
oder
als iterative Anwendung der zu
gehörenden Transformation
mit den Zeitpunkten als Iterationsindizes auffassen:
für alle
und bei
ist zusätzlich
für alle
Daher ist
bereits durch
eindeutig bestimmt und lässt sich einfacher
schreiben.
- Schränkt man bei einem kontinuierlichen dynamischen System
die Zeit auf
ein, dann ergibt sich mit
stets ein diskretes dynamisches System. Diese Diskretisierung findet zum einen in der Numerik eine große Anwendung, wie z.B. bei der Rückwärtsanalyse. Zum anderen existieren natürliche und technische Systeme, die durch nichtkontinuierliche Zustandsänderungen charakterisiert und in direkter Weise durch diskrete Dynamische Systeme modelliert werden können.
- Differenzierbare (Halb-)Flüsse sind (Halb-)Flüsse
, bei denen jede zu einem Zeitpunkt gehörende Transformation differenzierbar ist. Insbesondere ist jede dieser Transformationen eines differenzierbaren Flusses ein Diffeomorphismus.
- In der Theorie dynamischer Systeme interessiert man sich besonders für das
Verhalten von Trajektorien für
. Hierbei sind Limesmengen und deren Stabilität von großer Bedeutung. Die einfachsten Limesmengen sind Fixpunkte, das sind diejenigen Punkte
mit
für alle
, also diejenigen Zustände
, deren Bahn die einelementige Menge
ist. Weiter interessiert man sich für Punkte, deren Bahn für
gegen einen Fixpunkt konvergiert. Die wichtigsten Limesmengen sind neben Fixpunkten die periodischen Orbits. Gerade in nichtlinearen Systemen trifft man aber auch komplexe nichtperiodische Grenzmengen an. In der Theorie der nichtlinearen Systeme werden Fixpunkte, periodische Orbits und allgemeine nichtperiodische Grenzmengen unter dem Oberbegriff Attraktor (bzw. Repeller, falls abstoßend, subsumiert. Diese werden in der Chaostheorie ausführlich untersucht.
Wichtige Spezialfälle
Gewöhnliche Differentialgleichungen
Kontinuierliche dynamische Systeme treten vor allem im Zusammenhang mit gewöhnlichen Differentialgleichungen auf. Gegeben sei die autonome Differentialgleichung
mit einem Vektorfeld
auf einem Gebiet
.
Falls die Gleichung für alle Anfangswerte
eine für alle
definierte, eindeutig bestimmte Lösung
mit
besitzt, dann ist
mit
ein kontinuierliches dynamisches System. Die Bahnen des Systems sind also die
Lösungskurven der Differentialgleichung. Die Fixpunkte sind hier die
mit
;
sie werden auch stationäre oder kritische Punkte des Vektorfeldes
genannt.
Iteration
Diskrete dynamische Systeme stehen in enger Beziehung zur Iteration von Funktionen. Ist
eine Selbstabbildung
einer beliebigen Menge
,
also eine Funktion, die jedem
wieder ein Element
zuordnet, dann kann man zu einem Anfangswert
die rekursiv
definierte Folge
für
betrachten. Mit der
-fachen
Hintereinanderausführung
(
Mal) gilt dann
.
Die Gleichung
zeigt, dass damit
mit
ein diskretes dynamisches System ist. Umgekehrt wird für ein dynamisches System
durch
eine Abbildung
mit
definiert. Die Fixpunkte eines solchen Systems sind die
mit
.
Beispiel hierfür sind Markow-Ketten
in diskreter Zeit mit endlichem Zustandsraum .
Der Zustandsraum im Sinne eines dynamischen Systems sind dann alle
Wahrscheinlichkeitsvektoren
auf
,
die Zeit ist
und die Iteration ist gegeben durch die Linksmultiplikation des
Wahrscheinlichkeitsvektors
mit der Übergangsmatrix
.
Die Fixpunkte sind dann die stationären
Verteilungen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.01. 2026