Mathematisches Pendel

Schwingung eines Fadenpendels

Das mathematische Pendel oder ebene Pendel ist ein idealisiertes Pendel. Hierbei kann eine als punktförmig gedachte Masse, die mittels einer masselosen Pendelstange an einem Punkt aufgehängt ist, in einer vertikalen Ebene hin und her schwingen, wobei Reibungseffekte, insbesondere der Luftwiderstand vernachlässigt werden. Das ebene Pendel ist ein Spezialfall des Kugelpendels, das sich auch in andere Raumrichtungen bewegen kann. Da die Bewegung des Pendelkörpers auf einem vertikalen Kreis erfolgt, wird es auch als Kreispendel bezeichnet, obwohl damit häufiger das Kegelpendel gemeint ist.

In der Praxis kann man ein mathematisches Pendel dadurch annähern, dass man einen möglichst langen und dünnen Stab oder (falls die Auslenkung kleiner als 90° ist) einen dünnen Faden und einen möglichst kleinen und schweren Pendelkörper verwendet. Dass bei diesem Aufbau die Schwingungsweite (Amplitude) erst nach einer großen Anzahl Schwingungen spürbar zurückgeht, zeigt, dass hierbei die Reibung nur einen geringen Einfluss hat.

Pendel, welche die genannten Eigenschaften des mathematischen Pendels nicht nähererungsweise erfüllen, lassen sich durch das kompliziertere Modell des physikalischen Pendels beschreiben.

Die Schwingungsdauer ist unabhängig von der Masse des schwingenden Körpers. Bei kleinen Schwingungen ist die Schwingungsdauer auch nahezu unabhängig von der Größe der Amplitude. Hier zeigt das Pendel eine nahezu harmonische Schwingung, deren Schwingungsdauer ausschließlich von der Länge des Pendels und der herrschenden Fallbeschleunigung bestimmt wird. Die Schwingungsdauer verlängert sich bis ins Unendliche, je näher die Amplitude an 180° herankommt. Größere Anregungen führen zu „Überschlägen“, sodass der Pendelkörper sich periodisch im Kreis bewegt.

Mathematische Beschreibung

Bewegungsgleichung

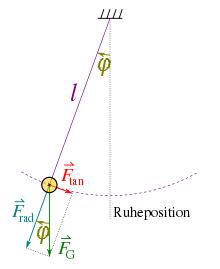
Die Rückstellkraft ist durch den tangentialen Anteil der Gewichtskraft gegeben, der mit Hilfe eines Sinus ermittelt werden kann: $F_{\mathrm {tan} }=F_{\mathrm {G} }\cdot \sin(\varphi )$

Anhand der Kräfte wird im Folgenden die Bewegungsgleichung der Pendelschwingung aufgestellt.

Aufgrund der Schwerkraft ( $F_{\mathrm {G} }=mg$ , = Schwerebeschleunigung) ergibt sich bei Auslenkung eines Fadenpendels der Masse eine Kraft $F_{\mathrm {tan} }(t)$ , die tangential zur kreisförmigen Pendelbahn wirkt. Die radiale Komponente spielt für die Bewegung keine Rolle, da sie in Richtung des Fadens wirkt. Da das mathematische Pendel nur einen Freiheitsgrad besitzt, genügt eine skalare Gleichung. Der Betrag der Rückstellkraft steigt mit dem Auslenkungswinkel $\varphi$ bezüglich der Ruhelage. Hierbei zeigt der Vektor der Rückstellkraft $F_{\mathrm {tan} }$ immer in Richtung der Ruheposition, daher ergibt sich ein Minus in folgender Gleichung:

$F_{\mathrm {tan} }(t)=-mg\cdot \sin \left(\varphi (t)\right)$

Beim Betrachten eines schwingenden Fadenpendels zeigt sich, dass die Geschwindigkeit mit zunehmender Auslenkung abnimmt und nach Erreichen des Scheitelpunkts die Richtung wechselt. Die Geschwindigkeitsänderung bedeutet, dass die Pendelmasse eine Beschleunigung erfährt, genauer gesagt findet eine Tangentialbeschleunigung statt, da eine kreisförmige Bewegungsbahn vorliegt. Die Bewegungsgleichung lautet nach dem 2. Newtonschen Gesetz:

$m\cdot a_{\mathrm {tan} }(t)=F_{\mathrm {tan} }(t)$

Die Tangentialbeschleunigung lässt sich durch die Winkelbeschleunigung ${\ddot \varphi }$ ausdrücken.

$a_\mathrm{tan}(t)= l \cdot \ddot{\varphi}(t)$

Bei der ungestörten Schwingung stellt die Rückstellkraft des Pendels die einzige äußere Kraft dar. Nach Umstellen und Kürzen der Masse entsteht eine nichtlineare Differentialgleichung zweiter Ordnung:

$m \cdot l \cdot \ddot{\varphi}(t) = - m \cdot g \cdot \sin \left(\varphi(t) \right)$

$\ddot{\varphi}(t) + \frac{g}{l} \cdot \sin \left(\varphi(t) \right) = 0$

die sich mit Hilfe der Winkelgeschwindigkeit $\omega$ auch als System von zwei gekoppelten Differentialgleichungen erster Ordnung schreiben lässt:

${\dot {\varphi }}=\omega$ ,

${\dot {\omega }}=-{\frac {g}{l}}\sin \varphi$ .

Bewegungsgleichung in kartesischen Koordinaten

Neben der Bewegungsgleichung mit dem Winkel $\varphi$ existieren weitere mögliche Beschreibungsformen. So lässt sich die Bewegung des mathematischen Pendels auch als Vektordifferentialgleichung mit kartesischen Koordinaten formulieren. Eine mögliche Herleitung erfolgt über den Lagrange-Formalismus mit Lagrange-Multiplikator. Die holonome Zwangsbedingung $f(x,y)=0$ findet sich dabei mit dem Gedanken, dass die Länge des Pendelarms der Länge des Ortsvektors entspricht. Da die Länge des Pendelarms beim mathematischen Pendel konstant ist muss folglich gelten:

$f(x,y)=x^{2}+y^{2}-l^{2}=0$

Anhand dieser holonomen Zwangsbedingung findet sich die unten stehende Vektordifferentialgleichung. Dabei stellt der erste Term die Zentripetalbeschleunigung und der zweite Term den an die Kreisbahn tangentiell wirkende Anteil der Erdbeschleunigung dar. In dieser Darstellung entfällt die Länge des Pendelarmes in der Differentialgleichung. Allerdings wird durch die Anfangswerte definiert, welche sich in Abhängigkeit von den Anfangswerten des Winkels $\varphi$ und der Winkelgeschwindigkeit ${\dot {\varphi }}$ darstellen lassen.

${\begin{bmatrix}{\ddot {x}}\\{\ddot {y}}\end{bmatrix}}=\underbrace {-{\frac {{\dot {x}}^{2}+{\dot {y}}^{2}}{x^{2}+y^{2}}}\cdot {\begin{bmatrix}x\\y\end{bmatrix}}} _{\text{Zentripetalbeschleunigung}}\;\;\;\underbrace {-{\frac {gx}{x^{2}+y^{2}}}\cdot {\begin{bmatrix}-y\\x\end{bmatrix}}} _{\text{Tangentielle Erdbeschleunigung}}\quad ,\quad \underbrace {{\begin{bmatrix}x_{0}\\y_{0}\end{bmatrix}}=l\cdot {\begin{bmatrix}-\sin \varphi _{0}\\\cos \varphi _{0}\end{bmatrix}}\quad ,\quad {\begin{bmatrix}{\dot {x}}_{0}\\{\dot {y}}_{0}\end{bmatrix}}=-l{\dot {\varphi }}_{0}\cdot {\begin{bmatrix}\cos \varphi _{0}\\\sin \varphi _{0}\end{bmatrix}}} _{\text{Anfangswerte}}$

Kleine Amplituden: Harmonische Schwingung

Kleinwinkelnäherung der Sinus-Funktion: Für $\varphi \approx 0$ ist $\sin (\varphi) \approx \varphi$ .

Für kleine Winkel gilt die Kleinwinkelnäherung:

$\sin (\varphi) \approx \varphi$ .

Durch Substitution ergibt sich somit eine lineare Differentialgleichung zweiter Ordnung der allgemeinen Form $\ddot x + \omega_0^2 x = 0 \$ , deren allgemeine Lösung $x(t) = u\, \sin(\omega_0 t +\phi)$ zur Schwingungsgleichung führt.

$\ddot{\varphi}(t) + \frac{g}{l} \cdot \varphi(t) = 0$

$\varphi (t)=\varphi _{\text{max}}\cdot \sin \left({\sqrt {\frac {g}{l}}}\cdot t+\alpha \right)$

Hierbei bezeichnen $\varphi _{\text{max}}$ die Winkelamplitude und $\alpha$ > den Nullphasenwinkel zum Zeitpunkt t=0 . Darüber hinaus sind die Eigenkreisfrequenz $\omega _{0}$ und die zugehörige Periodendauer $T_{0}$ ersichtlich.

$\omega_0 = \sqrt{\frac{g}{l}}$

$T_0 = 2 \pi \sqrt{\frac{l}{g}}$

Exakte Lösung

Abhängigkeit der Periode vom maximalen Auslenkungswinkel θ_c.

Da Pendel in der Realität immer mehr als infinitesimal ausgelenkt werden, verhalten sie sich nichtlinear, d.h. Schwingungen mit endlicher Amplitude sind anharmonisch. Die allgemeine Differentialgleichung ist elementar nicht lösbar und erfordert Kenntnisse über elliptische Funktionen und elliptische Integrale.

Gegeben ist die Differentialgleichung:

$\alpha (t)=-{\frac {g}{l}}\cdot \sin[\varphi (t)]$

Die Lösung für diese Differentialgleichung lässt sich über die Jacobische elliptische Funktion darstellen und sie lautet wie folgt:

$\varphi (t)=2\cdot \arctan[\tan({\frac {\varphi _{max}}{2}})\cdot \mathrm {cn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{max}}{2}})]]$

$\omega (t)=-{\sqrt {\frac {g}{l}}}\cdot \sin(\varphi _{max})\cdot \mathrm {sn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{max}}{2}})]/\mathrm {dn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{max}}{2}})]$

$\alpha (t)=-{\frac {g}{l}}\cdot \sin(\varphi _{max})\cdot \mathrm {cn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{max}}{2}})]/\mathrm {dn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{max}}{2}})]^{2}$

Der maximale Ausschlagswinkel $\varphi _{max}$ sollte weniger als 90° betragen.

$T(\varphi _{\text{max}})=4\cdot K[\sin({\frac {\varphi _{\text{max}}}{2}})]\cdot {\sqrt {\frac {l}{g}}}$

Damit lässt sich die allgemeine Lösung für die Periode in eine Reihe entwickeln:

${\begin{aligned}T(\varphi _{\text{max}})&=T_{0}\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{\left(2^{n}n!\right)^{2}}}\right)^{2}\sin ^{2n}\left(\varphi _{\text{max}}/2\right)\\&=T_{0}\cdot \left(1+\left({\frac {1}{2}}\right)^{2}\cdot \sin ^{2}\left({\frac {\varphi _{\text{max}}}{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\cdot \sin ^{4}\left({\frac {\varphi _{\text{max}}}{2}}\right)+\dots \right)\end{aligned}}$

Alternativ lässt sich das auftretende elliptische Integral auch über das arithmetisch-geometrische Mittel auswerten:

$T(\varphi _{\text{max}})=T_{0}\cdot {\frac {1}{M\left(1,\cos {\frac {\varphi _{\text{max}}}{2}}\right)}}$

Außerdem ist die Dämpfung durch Reibungsverluste bei einem echten Pendel größer als Null, so dass die Auslenkungen ungefähr exponentiell mit der Zeit abnehmen.

Dass die Periodendauer nicht von , sondern nur von dem Verhältnis $l/g$ abhängt, lässt sich auch aus einer Dimensionsanalyse, z.B. mit dem Buckinghamschen Π-Theorem, herleiten. Nur der numerische Faktor ( $2 \pi$ bei kleinen Amplituden, $\textstyle M\left(1,\cos {\tfrac {\hat {\varphi }}{2}}\right)$ in der exakten Lösung) ist so nicht zu ermitteln.

Der Winkel $\varphi$ als explizite Funktion der Zeit mit Startwinkel $\varphi _{0}$ und (positiver) Startgeschwindigkeit ${\hat {\omega }}$ lautet:

$\varphi (t)=2\operatorname {am} {\Bigg (}{\frac {2l\cdot \operatorname {F} {\Big (}{\frac {\varphi _{0}}{2}}{\Big |}{\frac {4g}{\xi }}{\Big )}-{\sqrt {l\cdot \xi }}\cdot t}{2l}}{\Bigg |}{\frac {4g}{\xi }}{\Bigg )}$

mit $\xi =2g+l\cdot {\hat {\omega }}^{2}-2g\cdot \cos(\varphi _{0})$ , wobei $\operatorname {am} ()$ die Jacobi-Amplitude und $\operatorname {F} ()$ das elliptische Integral 1. Art ist. Bei einer negativen ${\hat {\omega }}$ kann die Situation einfach gespiegelt werden, indem das Vorzeichen des Startwinkels vertauscht wird.

Numerische Lösung

Durch numerische Integration der beiden Differentialgleichungen 1. Ordnung lässt sich eine Näherungslösung rekursiv berechnen. Mit dem einfachsten Integrationsverfahren (Euler explizit) und der Schrittweite ergibt sich für die Winkelgeschwindigkeit:

$\omega _{k+1}=\omega _{k}-{\frac {g\cdot h}{l}}\cdot \sin \varphi _{k}\quad k=(0,1,2,\cdots ,k_{\text{max}})$

Für den Winkel kann die zuvor berechnete Winkelgeschwindigkeit benutzt werden:

$\varphi _{k+1}=\varphi _{k}+h\cdot \omega _{k+1}$

Die Anfangswerte für Winkelgeschwindigkeit und Winkel sind dem Index k=0 zugeordnet.

Die Genauigkeit der Lösung lässt sich durch Simulation über mehrere Perioden und Anpassung der Schrittweite überprüfen. Dieses Verfahren ist in der Physik auch als Methode der kleinen Schritte bekannt.

Erhaltungssätze

Beim mathematischen Pendel gilt der Energieerhaltungssatz der Mechanik. Auf dem Weg von der maximalen Auslenkung zur Ruhelage nimmt die potentielle Energie ab. Die mit ihr verbundene Gewichtskraft – genauer: deren tangentiale Komponente – verrichtet Beschleunigungsarbeit, wodurch die kinetische Energie zunimmt. Nach Durchschreiten des Minimums wirkt eine Komponente der Gewichtskraft entgegen der Bewegungsrichtung. Es wird Hubarbeit verrichtet.

$E_\mathrm{pot} + E_\mathrm{kin} = \text{konst.}\,$

Auch hieraus lässt sich die Differentialgleichung herleiten:

$E_\mathrm{pot} =m\;g\;l\cdot (1-\cos \varphi)$

$E_{\mathrm {kin} }={\frac {1}{2}}\cdot m\;(l\ {\dot {\varphi }})^{2}$

Die Summe ist zeitlich konstant, also

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}(E_{\mathrm {pot} }+E_{\mathrm {kin} })=0&=m\;g\;l\cdot \sin \varphi \cdot {\dot {\varphi }}+m\;l^{2}\cdot {\dot {\varphi }}\cdot {\ddot {\varphi }}\\&=m\;l^{2}\cdot {\dot {\varphi }}\cdot \left({\frac {g}{l}}\cdot \sin \varphi +{\ddot {\varphi }}\right)\end{aligned}}$

Diese Gleichung hat zwei Lösungen:

$\dot\varphi=0$ , es gibt keine Bewegung; diese Lösung kann man hier unbeachtet lassen.
$\frac gl\cdot\sin\varphi +\ddot\varphi=0$ ; diese Lösung stimmt mit der Lösung oben überein.

Anhand der Energieerhaltung kann die maximale Geschwindigkeit $v_{{\mathrm {max}}}$ der Pendelmasse nach Loslassen beim Winkel $\varphi$ berechnet werden:

$v_{\mathrm {max} }={\sqrt {2\cdot g\ \cdot l\cdot (1-\cos \varphi )}}$

Die maximale Geschwindigkeit wird im tiefsten Punkt der Pendelmasse erreicht, d.h. wenn der Faden senkrecht ist.

Gleichgewichtspunkte im Phasenraum

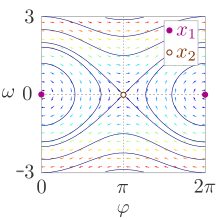
Phasenraum des ebenen Pendels mit g = l = 1. Der Phasenraum ist bezüglich des Winkels periodisch mit Periode 2π.

Gleichgewichtspositionen

Der Zustand des Systems lässt sich durch ein Tupel $x=(\varphi ,\omega )$ aus dem Winkel $\varphi$ und der Winkelgeschwindigkeit $\omega$ beschreiben.

Es gibt zwei Positionen $x_{1}=(0,0)$ und $x_{2}=(\pi ,0)$ , bei dem sich das System in einem mechanischen Gleichgewicht befindet. In beiden Punkten ist die Winkelgeschwindigkeit und die Summe aller angreifenden Kräfte und Momente Null. Der Gleichgewichtspunkt $x_{1}$ bei einem Winkel von Null ist das stabile Gleichgewicht, wenn das Pendel keine Auslenkung und Geschwindigkeit besitzt. Der zweite Punkt $x_{2}$ ist das instabile Gleichgewicht, wenn das Pendel keine Geschwindigkeit besitzt und „auf dem Kopf“ steht.

Literatur

Ekbert Hering, Rolf Martin, Martin Stohrer: Physik für Ingenieure. 8. Auflage. Springer, Berlin Heidelberg New York 2002, ISBN 3-540-42964-6.

Basierend auf einem Artikel in:

Wikipedia.de