Arithmetisch-geometrisches Mittel
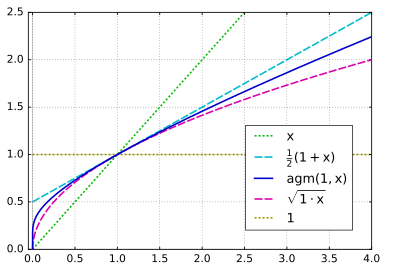
Plot
des arithmetisch-geometrischen Mittels

(in dunkelblau)
In der Mathematik bezeichnet man
als arithmetisch-geometrisches Mittel zweier positiver reeller Zahlen eine gewisse
Zahl, die zwischen dem arithmetischen
Mittel und dem geometrischen
Mittel liegt.
Definition
Es seien  und
und  zwei nichtnegative reelle
Zahlen. Ausgehend von ihnen werden induktiv zwei Folgen
zwei nichtnegative reelle
Zahlen. Ausgehend von ihnen werden induktiv zwei Folgen  und
und  mit
mit

|
(1a) |
|

|
(1b) |
|
definiert:
Die Folgen  und
und  konvergieren
gegen einen gemeinsamen Grenzwert
konvergieren
gegen einen gemeinsamen Grenzwert
 ,
der als arithmetisch-geometrisches Mittel von
,
der als arithmetisch-geometrisches Mittel von  und
und  bezeichnet wird.
bezeichnet wird.
Dass die beiden Grenzwerte tatsächlich existieren und darüber hinaus sogar
noch gleich sind, wird weiter unten in „Wichtige Eigenschaften“ gezeigt.
Einfaches Beispiel
Sei
 und
und 
|
(4a,b) |
|
Dann ist
 und
und 
|
(5) |
|
 und
und 
|
(6) |
|

|
(7) |
|
Einfache Eigenschaften
Für zwei nichtnegative Werte  und
und  gilt:
gilt:

|
(10) |
|
 für
für 
|
(11) |
|
Das heißt, das arithmetisch-geometrische Mittel ist – wie jede
Mittelwertfunktion – symmetrisch und homogen vom Grad 1 in seinen beiden
Variablen  und
und  .
.

|
(12) |
Gleichheit gilt dabei genau
für 
|

|
(13) |
|
Wichtige Eigenschaften
- Monotonie:
Für zwei positive Startwerte
 gilt nach der Ungleichung
vom arithmetischen und geometrischen Mittel stets auch
gilt nach der Ungleichung
vom arithmetischen und geometrischen Mittel stets auch  .
Die Folge
.
Die Folge  ist also monoton wachsend und durch
ist also monoton wachsend und durch  nach oben beschränkt, deshalb konvergiert sie gegen einen Grenzwert
nach oben beschränkt, deshalb konvergiert sie gegen einen Grenzwert  .
Andererseits ist die Folge
.
Andererseits ist die Folge  monoton fallend und nach unten beschränkt, das heißt, sie konvergiert gegen
einen Grenzwert
monoton fallend und nach unten beschränkt, das heißt, sie konvergiert gegen
einen Grenzwert  .
Oder anders geschrieben:
.
Oder anders geschrieben:

|
(14) |
|
Geht man nun in der Definitionsgleichung  zum Grenzwert über (das ist erlaubt, weil alle Grenzwerte existieren), dann
erhält man
zum Grenzwert über (das ist erlaubt, weil alle Grenzwerte existieren), dann
erhält man  ,
woraus
,
woraus  folgt. Somit sind die beiden Grenzwerte gleich und es ist
folgt. Somit sind die beiden Grenzwerte gleich und es ist  das arithmetisch-geometrische Mittel.
das arithmetisch-geometrische Mittel.

|
(15) |
Wegen der Abschätzung
|

|
(16) |
|
liegt ein Verfahren mit quadratischer Konvergenz vor.
Alternative Darstellung
Man kann beide Folgen auch voneinander "entkoppeln": Sei
Dann kann man die obigen Gleichungen umformen zu:

|
(22) |
|

|
(23) |
|
Historisches
Das arithmetisch-geometrische Mittel wurde unabhängig voneinander von den
Mathematikern Carl
Friedrich Gauß und zuvor schon von Adrien-Marie
Legendre entdeckt. Sie nutzten es, um die Bogenlänge von Ellipsen, also elliptische
Integrale, näherungsweise zu berechnen. Gauß etwa notierte zum Zusammenhang
zwischen dem arithmetisch-geometrischen Mittel und dem elliptischen Integral 1.
Gattung (Bogenlänge einer Lemniskate)
die Gleichung

|
(24) |
|
in sein Mathematisches Tagebuch.[1]
Verfahren von Salamin und Brent
Das nachfolgende Verfahren zur Berechnung der Kreiszahl
 wurde 1976 unabhängig voneinander von Richard
P. Brent und Eugene
Salamin publiziert. Es nutzt wesentlich die Erkenntnisse von Gauß über das
arithmetisch-geometrische Mittel. Gauß bemerkte zu seiner Zeit allerdings nicht,
dass sich damit auch ein schneller Algorithmus
zur Berechnung der Zahl
wurde 1976 unabhängig voneinander von Richard
P. Brent und Eugene
Salamin publiziert. Es nutzt wesentlich die Erkenntnisse von Gauß über das
arithmetisch-geometrische Mittel. Gauß bemerkte zu seiner Zeit allerdings nicht,
dass sich damit auch ein schneller Algorithmus
zur Berechnung der Zahl  konstruieren lässt. Dennoch wird das Verfahren oft auch als Methode von Gauß,
Brent und Salamin bezeichnet.
konstruieren lässt. Dennoch wird das Verfahren oft auch als Methode von Gauß,
Brent und Salamin bezeichnet.
Die Schritte des Verfahrens können folgendermaßen beschrieben werden:
- Initialisierung: Man verwendet als Startwerte

|
(31) |
|

berechnet man

|
(32) |
|

|
(33) |
|

|
(34) |
|

|
(35) |
|

|
(36) |
|
Die Folge der  konvergiert quadratisch gegen
konvergiert quadratisch gegen  ,
das heißt, dass mit jedem Durchlaufen der Schleife sich die Zahl der korrekt
berechneten Ziffern etwa verdoppelt. Damit konvergiert dieser Algorithmus
deutlich schneller gegen
,
das heißt, dass mit jedem Durchlaufen der Schleife sich die Zahl der korrekt
berechneten Ziffern etwa verdoppelt. Damit konvergiert dieser Algorithmus
deutlich schneller gegen  als viele klassische Verfahren.
als viele klassische Verfahren.
Zahlenbeispiel
Mit den Startwerten

|
(37) |
|
berechnet man iterativ:
Index 
|

|

|

|

|

|

|
1 |
0,70710 67811 86547 |
|
0,5 |
|

|
0,85355 33905 93274 |
0,84089 64152 53715 |
0,02144 66094 06726 |
0,45710 67811 86547 |
3,18767 26427 12110 |

|
0,84722 49029 23494 |
0,84720 12667 46891 |
0,00004 00497 56187 |
0,45694 65821 61801 |
3,14168 02932 97660 |

|
0,84721 30848 35193 |
0,84721 30847 52765 |
0,00000 00001 39667 |
0,45694 65810 44462 |
3,14159 26538 95460 |
Nach drei Iterationen erhält man für das arithmetisch-geometrische Mittel den
Näherungswert 
Für die Zahl  ergibt sich die Näherung
ergibt sich die Näherung 
Beziehung zu elliptischen Integralen
Es gilt:

|
(41) |
|
Die rechte Seite ist ein vollständiges elliptisches
Integral erster Art.
Anmerkungen
- ↑
Vgl. Carl Friedrich Gauß: Mathematisches
Tagebuch 1796–1814. Mit einer historischen Einführung von Kurt-R. Biermann.
Durchgesehen und mit Anmerkungen versehen von Hans Wußing und Olaf
Neumann. 5. Auflage. Harri Deutsch, Frankfurt am Main 2005. (Ostwalds
Klassiker der exakten Wissenschaften, Band 256.), Nr. 98 (Braunschweig, 30.
Mai 1798): „Terminum medium arithmetico-geometricum inter 1 et
 esse
esse  usque ad figuram undecimam comprobavimus, qua re demonstrata prorsus novus
campus in analysi certo aperietur.“ „Wir haben bis zur elften Stelle
nachgewiesen, daß der Wert des arithmetisch-geometrischen Mittels zwischen 1
und
usque ad figuram undecimam comprobavimus, qua re demonstrata prorsus novus
campus in analysi certo aperietur.“ „Wir haben bis zur elften Stelle
nachgewiesen, daß der Wert des arithmetisch-geometrischen Mittels zwischen 1
und  ist; durch diesen Beweis wird uns ganz gewiß ein völlig neues Feld in der
Analysis eröffnet werden.“ Dabei ist
ist; durch diesen Beweis wird uns ganz gewiß ein völlig neues Feld in der
Analysis eröffnet werden.“ Dabei ist  die von Gauß eingeführte lemniskatische
Konstante.
die von Gauß eingeführte lemniskatische
Konstante.
Basierend auf einem Artikel in:  Wikipedia.de
Seite zurück
Wikipedia.de
Seite zurück
© biancahoegel.de
Datum der letzten Änderung:
Jena, den: 03.06. 2021

und
zwei nichtnegative reelle
Zahlen. Ausgehend von ihnen werden induktiv zwei Folgen
und
mit
und
konvergieren
gegen einen gemeinsamen Grenzwert
,
der als arithmetisch-geometrisches Mittel von
und
bezeichnet wird.
und
gilt:
und
.
gilt nach der Ungleichung vom arithmetischen und geometrischen Mittel stets auch
. Die Folge
ist also monoton wachsend und durch
nach oben beschränkt, deshalb konvergiert sie gegen einen Grenzwert
. Andererseits ist die Folge
monoton fallend und nach unten beschränkt, das heißt, sie konvergiert gegen einen Grenzwert
. Oder anders geschrieben:
zum Grenzwert über (das ist erlaubt, weil alle Grenzwerte existieren), dann
erhält man
,
woraus
folgt. Somit sind die beiden Grenzwerte gleich und es ist
das arithmetisch-geometrische Mittel.
wurde 1976 unabhängig voneinander von Richard
P. Brent und Eugene
Salamin publiziert. Es nutzt wesentlich die Erkenntnisse von Gauß über das
arithmetisch-geometrische Mittel. Gauß bemerkte zu seiner Zeit allerdings nicht,
dass sich damit auch ein schneller Algorithmus
zur Berechnung der Zahl
konstruieren lässt. Dennoch wird das Verfahren oft auch als Methode von Gauß,
Brent und Salamin bezeichnet.
konvergiert quadratisch gegen
,
das heißt, dass mit jedem Durchlaufen der Schleife sich die Zahl der korrekt
berechneten Ziffern etwa verdoppelt. Damit konvergiert dieser Algorithmus
deutlich schneller gegen
als viele klassische Verfahren.
ergibt sich die Näherung
esse
usque ad figuram undecimam comprobavimus, qua re demonstrata prorsus novus campus in analysi certo aperietur.“ „Wir haben bis zur elften Stelle nachgewiesen, daß der Wert des arithmetisch-geometrischen Mittels zwischen 1 und
ist; durch diesen Beweis wird uns ganz gewiß ein völlig neues Feld in der Analysis eröffnet werden.“ Dabei ist
die von Gauß eingeführte lemniskatische Konstante.

