Ellipse

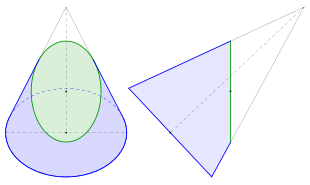
Ellipse mit Mittelpunkt , Brennpunkten $F_{1}$ und $F_{2}$ , Scheitelpunkten $S_{1},\dotsc ,S_{4}$ , Hauptachse (rot) und Nebenachse (grün)

Ellipse als Kegelschnitt.
Die Mittelachse des Kegels ist soweit geneigt, dass sich die Ellipse in der Seitenansicht von rechts in wahrer Größe zeigt.

Die Saturnringe erscheinen elliptisch.

Ellipsen sind in der Geometrie spezielle geschlossene ovale Kurven. Sie zählen neben den Parabeln und den Hyperbeln zu den Kegelschnitten. Eine anschauliche Definition verwendet die Eigenschaft, dass die Summe der Abstände eines Ellipsenpunktes von zwei vorgegebenen Punkten, den Brennpunkten, für alle Punkte gleich ist. Sind die Brennpunkte identisch, erhält man einen Kreis.

Jede Ellipse lässt sich in einem geeigneten Koordinatensystem durch eine Gleichung $\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ oder Parameterdarstellung $\;(a\cos t,b\sin t)\;$ beschreiben. Hieran erkennt man, dass man eine Ellipse als einen an der x-Achse um und an der y-Achse um gestreckten Einheitskreis auffassen kann.

Die Ellipse (von griechisch ἔλλειψις élleipsis ‚Mangel‘) wurde von Apollonios von Perge (etwa 262–190 v. Chr.) eingeführt und benannt, die Bezeichnung bezieht sich auf die Exzentrizität $\varepsilon <1$ .

Ellipsen treten nicht nur als ebene Schnitte eines Kegels auf. Auch auf Zylindern, Ellipsoiden, Hyperboloiden und elliptischen Paraboloiden gibt es Ellipsen.

In der Natur treten Ellipsen in Form von ungestörten keplerschen Planetenbahnen um die Sonne auf. Auch beim Zeichnen von Schrägbildern werden häufig Ellipsen benötigt, da ein Kreis durch eine Parallelprojektion im Allgemeinen auf eine Ellipse abgebildet wird.

Definition einer Ellipse als geometrischer Ort

Diese Grafik zeigt die im nachfolgenden Text verwendeten Bezeichnungen auf

Es gibt verschiedene Möglichkeiten, Ellipsen zu definieren. Neben der üblichen Definition über gewisse Abstände von Punkten ist es auch möglich, eine Ellipse als Schnittkurve zwischen einer entsprechend geneigten Ebene und einem Kegel zu bezeichnen (s. 1. Bild) oder als affines Bild des Einheitskreises.

Eine Ellipse ist der geometrische Ort aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten $F_{1}$ und $F_{2}$ gleich einer gegebenen Konstante ist. Diese Konstante wird üblicherweise mit bezeichnet. Die Punkte $F_{1}$ und $F_{2}$ heißen Brennpunkte:

$E=\{P\mid |PF_{2}|+|PF_{1}|=2a\}$

Um eine Strecke auszuschließen, setzt man voraus, dass größer als der Abstand $|F_{1}F_{2}|$ der Brennpunkte ist. Falls die beiden Brennpunkte zusammenfallen, ist ein Kreis mit Radius . Dieser einfache Fall wird in den folgenden Überlegungen oft stillschweigend ausgeschlossen, da die meisten Aussagen über Ellipsen im Kreisfall trivial werden.
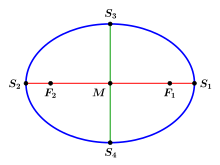
Der Mittelpunkt der Strecke ${\overline {F_{1}F_{2}}}$ heißt Mittelpunkt der Ellipse. Die Gerade durch die Brennpunkte ist die Hauptachse und die dazu orthogonale Gerade durch die Nebenachse. Die beiden Ellipsenpunkte $S_{1},\;S_{2}$ auf der Hauptachse sind die Hauptscheitel. Der Abstand der Hauptscheitel zum Mittelpunkt ist und heißt die große Halbachse. Die beiden Ellipsenpunkte $S_{3},\;S_{4}$ auf der Nebenachse sind die Nebenscheitel, und ihr Abstand zum Mittelpunkt ist jeweils die kleine Halbachse . 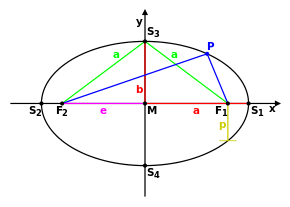Den Abstand der Brennpunkte zum Mittelpunkt nennt man die lineare Exzentrizität und $\varepsilon=e/a$ die numerische Exzentrizität. Mit dem Satz des Pythagoras gilt $a^{2}=e^{2}+b^{2}$ (siehe Zeichnung).

Ellipse: Definition mit Leitkreis

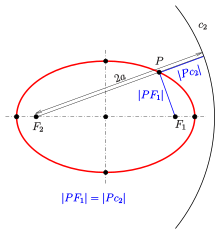
Die Gleichung $|PF_{2}|+|PF_{1}|=2a$ kann man auch so interpretieren: Wenn $c_{2}$ der Kreis um $F_{2}$ mit Radius ist, dann ist der Abstand des Punktes zum Kreis $c_{2}$ gleich dem Abstand des Punktes zum Brennpunkt $F_{1}$ :

$|PF_{1}|=|Pc_{2}|$

$c_{2}$ heißt Leitkreis der Ellipse bzgl. des Brennpunktes $F_{2}$ . Diese Eigenschaft sollte man nicht verwechseln mit der Leitlinieneigenschaft einer Ellipse (s. unten).

Mit Hilfe Dandelinscher Kugeln beweist man, dass gilt:

Jeder Schnitt eines Kegels mit einer Ebene, die die Kegelspitze nicht enthält, und deren Neigung kleiner als die der Mantellinien des Kegels ist, ist eine Ellipse.

Aufgrund der Leitkreis-Eigenschaft ist eine Ellipse die Äquidistanz-Kurve zu jedem ihrer Brennpunkte und dem Leitkreis mit dem anderen Brennpunkt als Mittelpunkt.

Ellipse in kartesischen Koordinaten

Gleichung

A. Führt man kartesische Koordinaten so ein, dass der Mittelpunkt der Ellipse im Ursprung liegt, die -Achse die Hauptachse ist, und

die Brennpunkte die Punkte $F_{1}=(e,0),\ F_{2}=(-e,0)$ ,

die Hauptscheitel $S_{1}=(a,0),\ S_{2}=(-a,0)$ sind,

so ergibt sich für einen beliebigen Punkt (x,y) der Abstand zum Brennpunkt (e,0) als $\sqrt{ (x-e)^2 + y^2 }$ und zum zweiten Brennpunkt $\sqrt{ (x+e)^2 + y^2 }$ . Also liegt der Punkt (x,y) genau dann auf der Ellipse, wenn die folgende Bedingung erfüllt ist:

${\sqrt {(x-e)^{2}+y^{2}}}+{\sqrt {(x+e)^{2}+y^{2}}}=2a$

Nach Beseitigung der Wurzeln durch geeignetes Quadrieren und Verwenden der Beziehung $b^{2}=a^{2}-e^{2}$ (s.o.) erhält man die Gleichung

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ oder nach aufgelöst

$y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}.$

$S_{3}=(0,b),\;S_{4}=(0,-b)$ sind die Nebenscheitel. Aus der Beziehung $b^{2}=a^{2}-e^{2}$ erhält man die Gleichungen

$e={\sqrt {a^{2}-b^{2}}}$ und $\varepsilon ={\frac {\sqrt {a^{2}-b^{2}}}{a}}\ .$

Daraus ergeben sich noch die Beziehungen

$b=a{\sqrt {1-\varepsilon ^{2}}}$

$p=a\cdot (1-\varepsilon ^{2})$

Ist a=b , so ist $\varepsilon =0$ und die Ellipse ein Kreis.
Ist b=e , so ist $\varepsilon ={\tfrac {1}{\sqrt {2}}}$ , und man nennt die Ellipse eine gleichseitige Ellipse oder Ellipse schönster Form.

B. Die Ellipse in A. lässt sich auch mithilfe einer Bilinearform als Lösungsmenge der Gleichung ${\vec {x}}^{\mathrm {T} }M\,{\vec {x}}=1$ auffassen. Hierbei werden die Vektoren und $x^{\mathrm {T} }$ mit dem gleichen Punkt identifiziert. Bei Einführung kartesischer Koordinaten ist die Matrix ${\begin{pmatrix}{\frac {1}{a^{2}}}&0\\0&{\frac {1}{b^{2}}}\end{pmatrix}}$ , ${\vec {x}}^{\mathrm {T} }=(x,y)$ ein Zeilenvektor und ${\vec {x}}={\begin{pmatrix}x\\y\end{pmatrix}}$ ein Spaltenvektor.

C. Eine Ellipse mit dem Mittelpunkt im Ursprung und den Brennpunkten auf der -Achse heißt auch in 1. Hauptlage. Wenn hier die obige Ellipsengleichung erwähnt wird, wird immer angenommen, dass $a\geq b$ und damit die Ellipse in 1. Hauptlage ist, was im „realen Leben“ aber nicht sein muss. Da kann durchaus auch a<b vorkommen, was bedeutet, dass die Ellipse sich in 2. Hauptlage befindet (die Brennpunkte liegen auf der -Achse).

Aufgrund der Definition einer Ellipse gilt:

Eine Ellipse ist symmetrisch zu ihren Achsen und damit auch zu ihrem Mittelpunkt.

(Die Symmetrieeigenschaft lässt sich auch leicht an der hier abgeleiteten Gleichung einer Ellipse erkennen.)

Halbparameter

Die halbe Länge einer Ellipsensehne, die durch einen Brennpunkt geht und zur Hauptachse senkrecht verläuft, nennt man den Halbparameter, manchmal auch nur Parameter oder auch semi-latus rectum (die Hälfte des latus rectum = $2\cdot p$ ) der Ellipse. Mit Hilfe der Gleichung einer Ellipse rechnet man leicht nach, dass

$p={\frac {b^{2}}{a}}$

gilt. Der Halbparameter hat noch die zusätzliche Bedeutung (s. unten): Der Krümmungsradius in den Hauptscheiteln ist .

Tangente

A. Für den Hauptscheitel (a,0) bzw. (-a,0) hat die Tangente die Gleichung x=a bzw. $x=-a$ . Die einfachste Weise, die Gleichung der Tangente in einem Ellipsenpunkt $(x_{0},y_{0}\neq 0)$ zu bestimmen, ist, die Gleichung ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ der Ellipse implizit zu differenzieren. Hiermit ergibt sich für die Ableitung

${\frac {2x}{a^{2}}}+{\frac {2yy'}{b^{2}}}=0\ \rightarrow \ y'=-{\frac {x}{y}}{\frac {b^{2}}{a^{2}}}$

und damit die Punkt-Steigungs-Form der Tangente im Punkt $(x_{0},y_{0})$ :

$y=-{\frac {x_{0}}{y_{0}}}{\frac {b^{2}}{a^{2}}}(x-x_{0})+y_{0}$

Berücksichtigt man ${\tfrac {x_{0}^{2}}{a^{2}}}+{\tfrac {y_{0}^{2}}{b^{2}}}=1$ , so erhält man als Gleichung der Tangente im Punkt $(x_{0},y_{0})$ :

${\frac {x_{0}}{a^{2}}}x+{\frac {y_{0}}{b^{2}}}y=1$

Diese Form schließt auch die Tangenten durch die Hauptscheitel ein. Letzteres gilt auch für die Vektorform

${\vec {x}}={\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}}+s\;{\begin{pmatrix}-ay_{0}/b\\bx_{0}/a\end{pmatrix}}\quad {\text{mit}}\quad s\in \mathbb {R}$ .

B. Die in A. eingeführte Tangentengleichung ${\tfrac {x_{0}}{a^{2}}}x+{\tfrac {y_{0}}{b^{2}}}y=1$ lässt sich auch ohne Differentialrechnung als Spezialfall einer Polarengleichung einführen (s.u. Herleitung der Lagebeziehungen von Pol und Polare, D.). Sie entspricht einer Normalenform mit dem Normalenvektor ${\vec {n}}=\left({\tfrac {x_{0}}{a^{2}}},{\tfrac {y_{0}}{b^{2}}}\right)$ . Von diesem lässt sich ein dazu rechtwinkeliger Richtungsvektor ${\vec {u}}$ von ablesen. Da ${\vec {u}}$ nur bis auf einen Skalar eindeutig ist, hat er die Formen

${\vec {u}}={\begin{pmatrix}-y_{0}/b^{2}\\x_{0}/a^{2}\end{pmatrix}}=$ ${\frac {1}{ab}}{\begin{pmatrix}-ay_{0}/b\\bx_{0}/a\end{pmatrix}}=$ $-{\frac {y_{0}}{b^{2}}}{\begin{pmatrix}1\\{\frac {-x_{0}}{y_{0}}}{\frac {b^{2}}{a^{2}}}\end{pmatrix}}$ ;

dies liefert den Richtungsvektor der in A. angegebenen Vektorform und auch die Steigung der dort angegebenen Punktsteigungsform.

Gleichung einer verschobenen Ellipse

Verschiebt man die obige Ellipse so, dass der Mittelpunkt der Punkt $(m_{1},m_{2})$ ist, ergibt sich die Mittelpunktsform einer Ellipse, deren Achsen parallel zu den Koordinatenachsen sind:

${\frac {(x-m_{1})^{2}}{a^{2}}}+{\frac {(y-m_{2})^{2}}{b^{2}}}=1$

Parameterdarstellungen

Standarddarstellung

Die übliche Parameterdarstellung einer Ellipse verwendet die Sinus- und Kosinus-Funktion. Wegen $\cos ^{2}t+\sin ^{2}t=1$ beschreibt

$(a\cos t,b\sin t),\ 0\leq t<2\pi$

die Ellipse ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1.$

Verschiedene Möglichkeiten, den Parameter geometrisch zu interpretieren, werden im Abschnitt Ellipsen zeichnen angegeben.

Rationale Parameterdarstellung

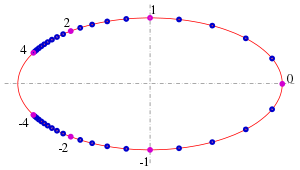
Punkte einer Ellipse mit Hilfe der rationalen Parameterdarstellung berechnet ( $\Delta u=0{,}2$ )

Mit der Substitution $u=\tan(t/2)$ und trigonometrischen Formeln erhält man

$\cos t=(1-u^{2})/(1+u^{2})\ ,\quad \sin t=2u/(1+u^{2})$

und damit die rationale Parameterdarstellung einer Ellipse:

${\begin{array}{lcl}x(u)&=&a(1-u^{2})/(1+u^{2})\\y(u)&=&2bu/(1+u^{2})\end{array}},\quad -\infty <u<\infty \;.$

Die rationale Parameterdarstellung hat folgende Eigenschaften (s. Bild):

Für wird der positive Hauptscheitel dargestellt: $x(0)=a,y(0)=0$ ; für der positive Nebenscheitel: $x(1)=0,y(1)=b$ .
Übergang zur Gegenzahl des Parameters spiegelt den dargestellten Punkt an der -Achse: $x(-u)=x(u),y(-u)=-y(u)$ ;
Übergang zum Kehrwert des Parameters spiegelt den dargestellten Punkt an der -Achse: $x\left({\tfrac {1}{u}}\right)=-x(u),y\left({\tfrac {1}{u}}\right)=y(u)$ .
Der negative Hauptscheitel kann mit keinem reellen Parameter dargestellt werden. Die Koordinaten desselben sind die Grenzwerte der Parameterdarstellung für unendliches positives oder negatives : $\lim _{u\to \pm \infty }x(u)=-a,\lim _{u\to \pm \infty }y(u)=0$ .

Rationale Parameterdarstellungen der Kegelschnitte (Ellipse, Hyperbel, Parabel) spielen im CAD-Bereich bei quadratischen rationalen Bezierkurven eine wichtige Rolle.

Tangentensteigung als Parameter

Eine Parameterdarstellung, die die Tangentensteigung in dem jeweiligen Ellipsenpunkt verwendet, erhält man durch Differentiation der Parameterdarstellung ${\vec {x}}(t)=(a\cos t,b\sin t)^{\mathrm {T} }$ :

${\vec {x}}'(t)=(-a\sin t,b\cos t)^{\mathrm {T} }\quad \rightarrow \quad m=-{\frac {b}{a}}\cot t\quad \rightarrow \quad \cot t=-{\frac {ma}{b}}.$

Mit Hilfe trigonometrischer Formeln ergibt sich

$\cos t={\frac {\cot t}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {-ma}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\ ,\quad \quad \sin t={\frac {1}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {b}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}.$

Ersetzt man in der Standarddarstellung $\cos t$ und $\sin t$ , erhält man schließlich

${\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\;,\;{\frac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right)^{\mathrm {T} },\,m\in \mathbb {R} .$

Dabei ist die Tangentensteigung im jeweiligen Ellipsenpunkt, ${\vec {c}}_{+}$ die obere und ${\vec {c}}_{-}$ die untere Hälfte der Ellipse. Die Punkte mit senkrechten Tangenten (Scheitel $(\pm a,0)$ ) werden durch diese Parameterdarstellung nicht erfasst.
Die Gleichung der Tangente im Punkt ${\vec c}_{\pm }(m)$ hat die Form $y=mx+n$ . Der -Abschnitt ergibt sich durch Einsetzen der Koordinaten des zugehörigen Ellipsenpunktes ${\vec c}_{\pm }(m)$ :

$y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}$

Diese Hauptform der Tangentengleichung ist ein wesentliches Hilfsmittel bei der Bestimmung der orthoptischen Kurve einer Ellipse.

Bemerkung. Die Hauptform der Tangentengleichung und die Koordinaten von ${\vec c}_{\pm }(m)$ lassen sich auch ohne Differentialrechnung und ohne trigonometrische Formeln herleiten, indem die Tangente als Spezialfall einer Polare aufgefasst wird (s.u. Herleitung der Lagebeziehungen von Pol und Polare, D.)

Verschobene Ellipse

Eine verschobene Ellipse mit Mittelpunkt $(m_{1},m_{2})$ wird durch

$(m_{1}+a\cos t\;,\;m_{2}+b\sin t),\ 0\leq t<2\pi$

beschrieben.

Eine Parameterdarstellung einer beliebigen Ellipse ist in dem Abschnitt Ellipse als affines Bild des Einheitskreises enthalten.

Eigenschaften

Brennpunkteigenschaft

→ Hauptartikel: Brennpunkt (Geometrie)

Brennpunkteigenschaft

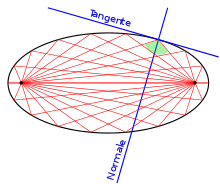
Die Verbindungslinie zwischen einem Brennpunkt und einem Punkt der Ellipse heißt Brennlinie, Leitstrahl oder Brennstrahl. Ihren Namen erhielten Brennpunkte und Brennstrahlen aufgrund der folgenden Eigenschaft:

Der Winkel zwischen den beiden Brennstrahlen in einem Punkt der Ellipse wird durch die Normale in diesem Punkt halbiert.
Anwendungen

Der Einfallswinkel, den der eine Brennstrahl mit der Tangente bildet, ist gleich dem Ausfallswinkel, den die Tangente mit dem anderen Brennstrahl bildet. Ein Lichtstrahl, der von einem Brennpunkt ausgeht, wird demnach an der Ellipsentangente so reflektiert, dass er den anderen Brennpunkt trifft. Bei einem ellipsenförmigen Spiegel treffen sich demnach alle von einem Brennpunkt ausgehenden Lichtstrahlen in dem anderen Brennpunkt.
Da der Weg von einem zum anderen Brennpunkt (entlang zweier zusammengehöriger Brennstrahlen) immer gleich lang ist, wird z.B. Schall nicht nur „verstärkt“ (siehe unten) von einem zum anderen Brennpunkt übertragen, sondern kommt sogar zeit- und phasengleich (also verständlich und nicht interferierend) dort an.
Die Tangente im Ellipsenpunkt ist die Winkelhalbierende des Außenwinkels. Da Winkelhalbierenden leicht zu konstruieren sind, bietet die Brennpunkteigenschaft eine einfache Methode, die Tangente in einem Ellipsenpunkt zu konstruieren.

Zwei Ellipsen mit denselben Brennpunkten $F_{1},\;F_{2}$ nennt man konfokal. Durch jeden Punkt, der nicht zwischen den Brennpunkten liegt, gibt es genau eine Ellipse mit den Brennpunkten $F_{1},\;F_{2}$ . Zwei konfokale Ellipsen haben keinen Schnittpunkt (s. Definition einer Ellipse).

Beweis der Brennpunkteigenschaft

Da die Tangente senkrecht zur Normalen verläuft, ist die obige Behauptung bewiesen, wenn die analoge Aussage für die Tangente gilt:

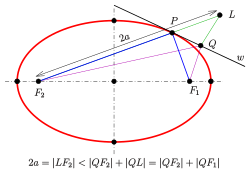
Die Tangente halbiert den Außenwinkel der Brennstrahlen

Der Außenwinkel der Brennstrahlen ${\overline {PF_{1}}},{\overline {PF_{2}}}$ in einem Ellipsenpunkt wird von der Tangente in diesem Punkt halbiert (s. Bild).

Es sei der Punkt auf der Geraden $\overline{PF_2}$ mit dem Abstand zum Brennpunk $F_{2}$ ( ist die große Halbachse der Ellipse). Die Gerade sei die Winkelhalbierende der Außenwinkel der Brennstrahlen ${\overline {PF_{1}}},{\overline {PF_{2}}}$ . Um nachzuweisen, dass die Tangente ist, zeigt man, dass auf kein weiterer Ellipsenpunkt liegen kann. Anhand der Zeichnung und der Dreiecksungleichung erkennt man, dass

$|QF_{2}|+|QF_{1}|=|QF_{2}|+|QL|>|LF_{2}|=2a$

gilt. Dies bedeutet, dass $|QF_{2}|+|QF_{1}|>2a$ ist. Wenn ein Punkt der Ellipse wäre, müsste die Summe aber gleich sein.

Bemerkung: Eine Beweis mit Mitteln der analytischen Geometrie befindet sich im Beweisarchiv.

Natürliches Vorkommen und Anwendung in der Technik:

Die Decken mancher Höhlen ähneln einer Ellipsenhälfte. Befindet man sich – mit den Ohren – in einem Brennpunkt dieser Ellipse, hört man jedes Geräusch, dessen Ursprung im zweiten Brennpunkt liegt, verstärkt („Flüstergewölbe“). Diese Art der Schallübertragung funktioniert in einigen Stationen der Pariser Métro sogar von Bahnsteig zu Bahnsteig. Das gleiche Prinzip der Schallfokussierung wird heute zur Zertrümmerung von Nierensteinen mit Stoßwellen verwendet. Auch im lampengepumpten Nd:YAG-Laser wird ein Reflektor in Form einer Ellipse verwendet. Die Pumpquelle – entweder eine Blitzlampe oder eine Bogenlampe – wird in dem einen Brennpunkt positioniert, und der dotierte Kristall wird in den anderen Brennpunkt gelegt.

Direktrix

Ellipse mit Leitlinien

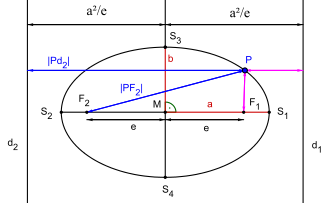
Für eine echte Ellipse, d.h. $e>0$ , bezeichnet man eine Parallele zur Nebenachse im Abstand $a^{2}/e$ als Direktrix oder Leitlinie. Für einen beliebigen Punkt der Ellipse ist das Verhältnis seines Abstands von einem Brennpunkt zu dem Abstand von der Direktrix auf der entsprechenden Seite der Nebenachse gleich der numerischen Exzentrizität:

$|PF_{1}|:|Pd_{1}|=|PF_{2}|:|Pd_{2}|=\varepsilon .$ Es ist $\varepsilon >0.$

Beweis:
Mit ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\Leftrightarrow y^{2}=b^{2}-{\tfrac {b^{2}x^{2}}{a^{2}}}$ sowie $e^{2}+b^{2}=a^{2}$ und den binomischen Formeln ist

$|PF_{1,2}|^{2}=(x\mp e)^{2}+y^{2}=$

${(x\mp e)^{2}+b^{2}-{\frac {b^{2}x^{2}}{a^{2}}}={\frac {a^{2}x^{2}}{a^{2}}}\mp 2ex+e^{2}+b^{2}-{\frac {b^{2}x^{2}}{a^{2}}}={\frac {e^{2}x^{2}}{a^{2}}}\mp 2{\frac {ex}{a}}\cdot a+a^{2}=\left({\frac {ex}{a}}\mp {\frac {ea^{2}}{ae}}\right)^{2}=}$

$\left({\frac {e}{a}}\right)^{2}\left(x\mp {\frac {a^{2}}{e}}\right)^{2}=\varepsilon ^{2}|Pd_{1,2}|^{2}$ .

Die Umkehrung dieser Aussage gilt auch und kann zu einer weiteren Definition einer Ellipse benutzt werden (ähnlich wie bei einer Parabel):

Für einen Punkt (Brennpunkt), eine Gerade (Leitlinie) nicht durch und eine reelle Zahl $\varepsilon$ mit $0 < \varepsilon < 1$ ist die Menge der Punkte (geometrischer Ort), für die der Quotient der Abstände zu dem Punkt und der Geraden gleich $\varepsilon$ ist, eine Ellipse:

$E=\{P\mid {\frac {|PF|}{|Pd|}}=\varepsilon \}$

Die Wahl $\varepsilon=0$ , also die Exzentrizität eines Kreises, ist in diesem Zusammenhang nicht erlaubt. Man kann als Leitlinie eines Kreises die unendlich entfernte Gerade auffassen.

Kegelschnittschar mit einem gemeinsamen Scheitel und einem gemeinsamen Halbparameter

Beweis:

Es sei $F=(f,0),\ \varepsilon >0$ und (0,0) ein Punkt der Kurve. Die Leitlinie hat die Gleichung $x=-\tfrac{f}{\varepsilon}$ . Mit P=(x,y) und der Beziehung $|PF|^{2}=\varepsilon ^{2}|Pd|^{2}$ ergibt sich

$(x-f)^{2}+y^{2}=\varepsilon ^{2}(x+{\tfrac {f}{\varepsilon }})^{2}=(\varepsilon x+f)^{2}$ und $x^2(\varepsilon^2-1)+2xf(1+\varepsilon)-y^2=0.$

Die Substitution $p=f(1+\varepsilon)$ liefert

$x^2(\varepsilon^2-1)+2px-y^2=0.$

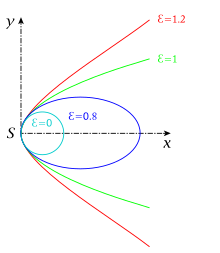
Dies ist die Gleichung einer Ellipse ( $\varepsilon<1$ ) oder einer Parabel ( $\varepsilon =1$ ) oder einer Hyperbel ( $\varepsilon>1$ ). All diese nicht-ausgearteten Kegelschnitte haben den Ursprung als Scheitel gemeinsam (s. Bild).

Für $\varepsilon<1$ führt man neue Parameter $a={\tfrac {p}{1-\varepsilon ^{2}}}$ und $b^{2}=ap\Rightarrow 1-\varepsilon ^{2}={\tfrac {b^{2}}{a^{2}}}$ ein; die obige Gleichung wird dann zu

${\frac {(x-a)^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\ ,$

was die Gleichung einer Ellipse mit Mittelpunkt (a,0) , der -Achse als Hauptachse und den Halbachsen a,b ist.

Allgemeiner Fall:

Für den Brennpunkt $F=(f_{1},f_{2})$ und die Leitlinie $ux+vy+w=0$ erhält man die Gleichung

$\left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}=\varepsilon ^{2}\cdot {\frac {\left(ux+vy+w\right)^{2}}{u^{2}+v^{2}}}.$

Die rechte Seite der Gleichung benutzt die Hessesche Normalform einer Geraden, um den Abstand eines Punktes von einer Gerade zu berechnen.

Konjugierte Durchmesser

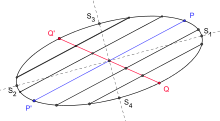
Ellipse mit zwei konjugierten Durchmessern

Betrachtet man zu einem beliebigen Ellipsendurchmesser (einer Ellipsensehne durch den Ellipsenmittelpunkt) ${\overline {PP'}}$ alle parallelen Sehnen, so liegen deren Mittelpunkte ebenfalls auf einem Ellipsendurchmesser ${\overline {QQ'}}$ . Man nennt ${\overline {QQ'}}$ den zu ${\overline {PP'}}$ konjugierten Durchmesser.
Bildet man zum konjugierten Durchmesser erneut den konjugierten Durchmesser, so erhält man wieder den ursprünglichen. In der Zeichnung stimmt also der zu ${\overline {QQ'}}$ konjugierte Durchmesser mit dem ursprünglichen Durchmesser ${\overline {PP'}}$ überein.
Die Tangenten in den Endpunkten eines Durchmessers (etwa ${\overline {PP'}}$ ) sind parallel zum konjugierten Durchmesser (im Beispiel ${\overline {QQ'}}$ ).
Haupt- und Nebenachse sind das einzige Paar orthogonaler konjugierter Durchmesser.
Ist die Ellipse ein Kreis, so sind genau die orthogonalen Durchmesser (auch) konjugiert.
Sind konjugierte Durchmesser nicht orthogonal, so ist das Produkt ihrer Steigungen ${\tfrac {-b^{2}}{a^{2}}}$ .
Seien $d_{1}$ , $d_{2}$ konjugierte Durchmesser. Dann ist $\left({\tfrac {d_{1}}{2}}\right)^{2}+\left({\tfrac {d_{2}}{2}}\right)^{2}=a^{2}+b^{2}$ . (Satz des Apollonius)

Konjugierte Durchmesser (erstrangig von Ellipsen) werden auch auf einer eigenen Wikipedia-Seite behandelt, ebenso der Satz des Apollonius (samt Beweis). Ein analytischer Gesamt-Beweis sämtlicher hier aufgeführter Aussagen, der von der gemeinsamen Bilinearform zweier Ursprungsgeraden ausgeht, findet sich im Beweisarchiv. Dieser Beweis benötigt weder trigonometrische Funktionen noch Parameterdarstellungen noch eine affine Abbildung.

Eine Anwendungsmöglichkeit im Bereich des technischen Zeichnens besteht in der Möglichkeit, den höchsten Punkt einer Ellipse oder eines Ellipsenbogens beliebiger Lage über einer Linie zu finden – nützlich z.B. für korrekte 2D-Darstellungen nicht-orthogonaler Ansichten zylindrischer Körper oder abgerundeter Kanten ohne Verwendung von 3D-Programmen. Wichtig ist dies für den sauberen Anschluss tangential von der Ellipse weg laufender Linien. Hierzu sind in die Ellipse oder den Ellipsenbogen zwei Sehnen parallel zur gewünschten Tangentenrichtung und die durch die Mittelpunkte der beiden Sehnen definierte Linie des zugehörigen konjugierten Durchmessers einzuzeichnen. Der Schnittpunkt dieser Linie mit der Ellipse oder dem Ellipsenbogen definiert den Anschlusspunkt der Tangente (und normalerweise den Endpunkt des Ellipsenbogens).

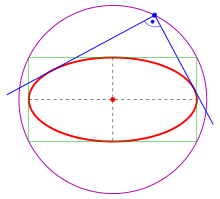
Ellipse mit orthoptischer Kurve (lila)

Orthogonale Tangenten

→ Hauptartikel: Orthoptische Kurve

Für die Ellipse $\tfrac{x^2}{a^2}+\tfrac{y^2}{b^2}=1$ liegen die Schnittpunkte orthogonaler Tangenten auf dem Kreis $x^{2}+y^{2}=a^{2}+b^{2}$ .

Diesen Kreis nennt man die orthoptische Kurve der gegebenen Ellipse, es ist der Umkreis des Rechtecks, das die Ellipse umschreibt.

Pol-Polare-Beziehung

Führt man kartesische Koordinaten so ein, dass der Mittelpunkt der Ellipse im Ursprung liegt, so kann eine beliebige Ellipse mit der Gleichung ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ beschrieben werden (s.o. Abschnitt Gleichung). Weiter ordnet für eine vorgegebene Ellipse eine Funktion je einem Punkt P_0=(x_0,y_0) die Gerade ${\frac {x_{0}x}{a^{2}}}+{\frac {y_{0}y}{b^{2}}}=1$ zu. Bezüglich heißt $P_{0}$ Pol, die zugeordnete Gerade Polare. ist eine Bijektion; die inverse Funktion bildet je eine Polare auf einen Pol ab. Der Ellipsenmittelpunkt (0,0) ist in keiner so definierten Polare enthalten, entsprechend existiert zu (0,0) keine Polare. Die angegebene Gleichung der Polare lässt sich als Normalenform mit dem zugehörigen Normalenvektor $\left({\tfrac {x_{0}}{a^{2}}},{\tfrac {y_{0}}{b^{2}}}\right)$ auffassen.

Eine solche Beziehung zwischen Punkten und Geraden, die durch einen Kegelschnitt vermittelt wird, nennt man Pol-Polare-Beziehung oder einfach Polarität. Pol-Polare-Beziehungen gibt es auch für Hyperbeln und Parabeln, siehe auch Pol und Polare.

Ellipse: Pol-Polare-Beziehung

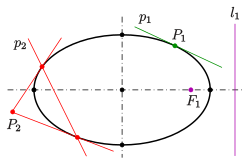
Zu Pol und Polare gelten folgende Lagebeziehungen:

Der Brennpunkt und die Leitlinie $x={\tfrac {a^{2}}{e}}$ bilden eine Polarität. (1)
Genau dann, wenn der Pol außerhalb der Ellipse liegt, hat die Polare zwei Punkte mit der Ellipse gemeinsam (s. Bild: $P_2,\ p_2$ ). (2)
Genau dann, wenn der Pol auf der Ellipse liegt, hat die Polare genau einen Punkte mit der Ellipse gemeinsam (= die Polare ist eine Tangente; s. Bild: $P_1,\ p_1$ ). (3)
Genau dann, wenn der Pol innerhalb der Ellipse liegt, hat die Polare keinen Punkt mit der Ellipse gemeinsam (s. Bild: $F_{1},\ l_{1}$ ). (4)
Jeder gemeinsame Punkt einer Polare und einer Ellipse ist Berührpunkt einer Tangente vom zugehörigen Pol an die Ellipse (s. Bild: $P_2,\ p_2$ ). (5)
Der Schnittpunkt zweier Polaren ist der Pol der Gerade durch die Pole. (6)

Herleitung der Lagebeziehungen von Pol und Polare; alternative Herleitung einer Tangenten- und einer Ellipsengleichung

A. Ist eine Polare parallel zur -Achse, so hat sie auch die Form $0\neq c=x\Leftrightarrow {\frac {1}{c}}\cdot x+0\cdot y=1$ . Mit dem zugehörigen Normalenvektor $\left({\tfrac {x_{0}}{a^{2}}}={\tfrac {1}{c}},{\tfrac {y_{0}}{b^{2}}}=0\right)$ ist der zugehörige Pol $\left(x_{0}={\tfrac {a^{2}}{c}},y_{0}=0\right).$ Insbesondere folgt für $x_{0}={\tfrac {a^{2}}{c}}=e\Leftrightarrow c={\tfrac {a^{2}}{e}}$ die Polarität (1) von Brennpunkt und Direktrix.

Einsetzen der betrachteten Polare in die Mittelpunktform einer Ellipse ergibt für die Ordinate eines beliebigen Schnittpunkts die Bedingung ${\tfrac {c^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ ; die Diskriminante dieser quadratischen Gleichung in hat bis auf einen positiven Faktor die Form

$T_{1}=\left({\frac {a^{2}}{c^{2}}}-1=\right)\quad \ {\frac {x_{0}^{2}}{a^{2}}}-1$ .

B. Ist eine Polare nicht parallel zur -Achse, so hat sie die Hauptform $y=mx+n$ . Wegen $n \neq 0$ lässt sich diese in die Normalenform $-mx/n+y/n=1$ umformen. Vergleich mit der Normalenform ergibt als Darstellung Koordinaten des Pols mit den Parametern der Hauptform:

$x_{0}=-{\frac {ma^{2}}{n}},\quad \ y_{0}={\frac {b^{2}}{n}}$ .

Einsetzen der Hauptform $y=mx+n$ in die Mittelpunktform einer Ellipse ergibt für die Abszisse eines beliebigen Schnittpunkts die Bedingung ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {(mx+n)^{2}}{b^{2}}}=1$ ; die Diskriminante dieser quadratischen Gleichung in hat bis auf einen positiven Faktor die Form

$T_{2}=\left({\frac {m^{2}a^{2}}{n^{2}}}+{\frac {b^{2}}{n^{2}}}-1=\right)\quad \ {\frac {x_{0}^{2}}{a^{2}}}+{\frac {y_{0}^{2}}{b^{2}}}-1.$

C. Insgesamt erlaubt der Term $T=T_{1}$ bzw. $T=T_{2}$ für eine beliebige Polare folgende Unterscheidung paarweise disjunkter Fälle:

Für $T<0$ hat die Polare mit der Ellipse keinen Punkt gemeinsam, und der Pol liegt innerhalb der Ellipse. Hieraus folgt (2).
Für hat die Polare mit der Ellipse genau einen Punkt gemeinsam, und der Pol liegt auf der Ellipse. Also ist die Polare eine Tangente an die Ellipse, der Pol ihr Berührpunkt (s. Bild: $P_1,\ p_1$ ). Hieraus folgt (3).
Für hat die Polare mit der Ellipse zwei Punkte gemeinsam, und der Pol liegt außerhalb der Ellipse. Hieraus folgt (4).

D. Ist eine Tangente nicht senkrecht, so ergibt Auflösung der Gleichung $T_{2}=0$ nach und Einsetzen von die Hauptform der Tangente:

$\quad \ y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ ;

Einsetzen von in die Koordinaten $x_{0}=-{\tfrac {ma^{2}}{n}},y_{0}={\tfrac {b^{2}}{n}}$ des Berührpunkts ergibt die Koordinaten der Parameterdarstellung einer Ellipse mit der Steigung als Parameter: $\quad \ {\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\;,\;{\frac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right)^{\mathrm {T} },\,m\in \mathbb {R}$ ;

diese Parameterdarstellung erfasst die Hauptscheitel nicht.

E. Ausgehend von der im Abschnitt „Gleichung“, B. aufgeführten Bilinearform der Ellipse hat die Polare zum Punkt die Normalenformen

${\vec {p}}^{\mathrm {T} }M{\vec {x}}=1$ mit dem Normalenvektor ${\vec {n}}^{\mathrm {T} }={\vec {p}}^{\mathrm {T} }M$ und

${\vec {x}}^{\mathrm {T} }M{\vec {p}}=1$ mit dem Normalenvektor $M{\vec {p}}={\vec {n}}$ .

Ist ein Punkt der Ellipse, so beschreiben auch diese Gleichungen eine Tangente.

Diese koordinatenfreie rechnerische Darstellung der Polare eignet sich für Beweise. Mit den Koordinatendarstellungen $P(x_{0},y_{0})$ und X(x,y) sowie den im Abschnitt „Gleichung“ angegebenen Matrizenkoordinaten für entsteht durch Auswertung der Matrizenprodukte wieder die im Abschnitt Pol-Polare-Beziehung angegebene Gleichung ${\tfrac {x_{0}}{a^{2}}}x+{\tfrac {y_{0}}{b^{2}}}y=1$ .

Beweis von (5) („Jeder gemeinsame Punkt einer Polare und einer Ellipse ist Berührpunkt einer Tangente vom zugehörigen Pol an die Ellipse.“):
Da die Ellipsenpunkte $S_{1},S_{2}$ auf der Polare zu liegen, gilt ${\vec {s}}_{1}^{\mathrm {T} }M{\vec {p}}=1$ und ${\vec {s}}_{2}^{\mathrm {T} }M{\vec {p}}=1$ . Fasst man in diesen Gleichungen nicht $M{\vec {p}}$ , sondern ${\vec {s}}_{1}^{\mathrm {T} }M$ bzw. ${\vec {s}}_{2}^{\mathrm {T} }M$ als Normalenvektor auf, so besagen sie, dass die Tangenten in den Ellipsenpunkten $S_{1},S_{2}$ den Punkt gemeinsam haben.

Beweis von (6) („Der Schnittpunkt zweier Polaren ist der Pol der Gerade durch die Pole.“):
Für einen Schnittpunkt zweier Polaren zu $P_{1}$ und $P_{2}$ gilt ${\vec {s}}^{\mathrm {T} }M{\vec {p}}_{1}=1$ und ${\vec {s}}^{\mathrm {T} }M{\vec {p}}_{2}=1$ . Fasst man in diesen Gleichungen nicht $M{\vec {p}}_{1}$ bzw. $M{\vec {p}}_{2}$ , sondern ${\vec {s}}^{\mathrm {T} }M={\vec {n}}^{\mathrm {T} }$ als Normalenvektor auf, so besagen sie, dass auf der Polare zu die Punkte $P_{1}$ , $P_{2}$ liegen. Weiter zeigt die Betrachtung der Parameterform ${\vec {x}}={\vec {p}}_{1}+\lambda ({\vec {p}}_{2}-{\vec {p}}_{1})$ mit

${\vec {n}}^{\mathrm {T} }{\vec {x}}={\vec {n}}^{\mathrm {T} }{\vec {p}}_{1}+\lambda ({\vec {n}}^{\mathrm {T} }{\vec {p}}_{2}-{\vec {n}}^{\mathrm {T} }{\vec {p}}_{1})=1+\lambda (1-1)=1={\vec {s}}^{\mathrm {T} }M{\vec {x}}$

die punktweise Gleichheit der Gerade $(P_{1}P_{2})$ mit der Polare zu .

Ellipse als affines Bild des Einheitskreises

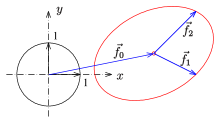
Eine andere Definition der Ellipse benutzt eine spezielle geometrische Abbildung, nämlich die Affinität. Hier ist die Ellipse als affines Bild des Einheitskreises definiert.

Parameterdarstellung

Eine affine Abbildung in der reellen Ebene hat die Form ${\vec {x}}\to {\vec {f}}_{0}+A{\vec {x}}$ , wobei eine reguläre Matrix (Determinante nicht 0) und ${\vec {f}}_{0}$ ein beliebiger Vektor ist. Sind ${\vec {f}}_{1},\;{\vec {f}}_{2}$ die Spaltenvektoren der Matrix , so wird der Einheitskreis $(\cos t,\sin t),0\leq \ t\leq 2\pi ,$ auf die Ellipse

${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t$

abgebildet. ${\vec {f}}_{0}$ ist der Mittelpunkt und ${\vec {f}}_{1},\;{\vec {f}}_{2}$ sind zwei konjugierte Halbmesser (s.u.) der Ellipse. ${\vec {f}}_{1},\;{\vec {f}}_{2}$ stehen i.A. nicht senkrecht aufeinander. D.h., ${\vec {f}}_{0}\pm {\vec {f}}_{1}$ und ${\vec {f}}_{0}\pm {\vec {f}}_{2}$ sind i.A. nicht die Scheitel der Ellipse. Diese Definition einer Ellipse liefert eine einfache Parameterdarstellung (s.u.) einer beliebigen Ellipse.

Scheitel, Scheitelform

Da in einem Scheitel die Tangente zum zugehörigen Ellipsendurchmesser senkrecht steht und die Tangentenrichtung in einem Ellipsenpunkt ${\vec {p}}'(t)=-{\vec {f}}_{1}\sin t+{\vec {f}}_{2}\cos t$ ist, ergibt sich der Parameter $t_{0}$ eines Scheitels aus der Gleichung

${\vec {p}}'(t)\cdot ({\vec {p}}(t)-{\vec {f}}_{0})=(-{\vec {f}}_{1}\sin t+{\vec {f}}_{2}\cos t)\cdot ({\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t)=0$

und damit aus $\cot(2t_{0})={\tfrac {{\vec {f}}_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}$ .
(Es wurden die Formeln $\cos ^{2}t-\sin ^{2}t=\cos 2t,\ 2\sin t\cos t=\sin 2t$ benutzt.)

Falls ${\vec {f}}_{1}\cdot {\vec {f}}_{2}=0$ ist, ist $t_{0}=0$ und die Parameterdarstellung schon in Scheitelform.

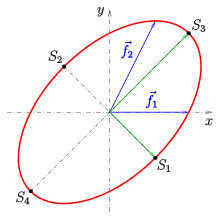
Die 4 Scheitel der Ellipse sind ${\vec {p}}(t_{0}),{\vec {p}}(t_{0}\pm {\frac {\pi }{2}}),{\vec {p}}(t_{0}+\pi ).$

Die Scheitelform der Parameterdarstellung der Ellipse ist

${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+({\vec {p}}(t_{0})-{\vec {f}}_{0})\cos(t-t_{0})+({\vec {p}}(t_{0}+{\tfrac {\pi }{2}})-{\vec {f}}_{0})\sin(t-t_{0}).$

Beispiele

Ellipse: Transformation auf Scheitelform (Beispiel 3)

$\vec f_0=\begin{pmatrix} 0 \\ 0 \end{pmatrix},\ \vec f_1=\begin{pmatrix} a \\ 0 \end{pmatrix},\ \vec f_2=\begin{pmatrix} 0 \\ b \end{pmatrix}$ liefert die übliche Parameterdarstellung der Ellipse mit der Gleichung ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1:\quad {\vec {x}}={\vec {p}}(t)={\begin{pmatrix}a\cos t\\b\sin t\end{pmatrix}}$ .
${\vec {f}}_{0}={\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}},\ {\vec {f}}_{1}={\begin{pmatrix}a\cos \varphi \\a\sin \varphi \end{pmatrix}},\ {\vec {f}}_{2}={\begin{pmatrix}-b\sin \varphi \\b\cos \varphi \end{pmatrix}}$ liefert die Parameterdarstellung der Ellipse, die aus ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ durch Drehung um den Winkel $\varphi$ und anschließende Verschiebung um ${\vec {f}}_{0}$ hervorgeht. Die Parameterdarstellung ist schon in Scheitelform. D.h., ${\vec {f}}_{0}\pm {\vec {f}}_{1}$ und ${\vec {f}}_{0}\pm {\vec {f}}_{2}$ sind die Scheitel der Ellipse.
Die Parameterdarstellung

${\vec {x}}={\vec {p}}(t)={\begin{pmatrix}{\sqrt {3}}\\0\end{pmatrix}}\cos t+{\begin{pmatrix}1\\2\end{pmatrix}}\sin t$

einer Ellipse ist nicht in Scheitelform.

Der Scheitelparameter ergibt sich aus $\cot(2t_{0})=-{\tfrac {1}{\sqrt {3}}}$ zu $t_{0}=-{\tfrac {\pi }{6}}$ .

Die Scheitelform der Parameterdarstellung ist:

${\vec {x}}={\vec {p}}(t)={\begin{pmatrix}\ 1\\-1\end{pmatrix}}\cos(t+{\tfrac {\pi }{6}})+{\sqrt {3}}{\begin{pmatrix}1\\1\end{pmatrix}}\sin(t+{\tfrac {\pi }{6}})$

Die Scheitel sind: $(1,-1),(-1,1),({\sqrt {3}},{\sqrt {3}}),(-{\sqrt {3}},-{\sqrt {3}})$ und

die Halbachsen: $a={\sqrt {2}},\ b={\sqrt {6}}.$

Implizite Darstellung

Löst man die Parameterdarstellung mit Hilfe der Cramerschen Regel nach $\;\cos t,\sin t\;$ auf und verwendet $\;\cos ^{2}t+\sin ^{2}t-1=0\;$ , erhält man die implizite Darstellung

$\det({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2})^{2}+\det({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0})^{2}-\det({\vec {f}}\!_{1},{\vec {f}}\!_{2})^{2}=0$ .

Ellipse im Raum

Sind die Vektoren ${\vec {f}}_{0},\;{\vec {f}}_{1},\;{\vec {f}}_{2}$ aus dem $\mathbb {R} ^{3}$ , so erhält man eine Parameterdarstellung einer Ellipse im Raum.

Peripheriewinkelsatz und 3-Punkteform für Ellipsen

Kreise

Kreis: Peripheriewinkelsatz

Ein Kreis mit der Gleichung $(x-c)^{2}+(y-d)^{2}=r^{2},\ r>0$ ist durch drei Punkte $(x_{1},y_{1}),\;(x_{2},y_{2}),\;(x_{3},y_{3})$ nicht auf einer Geraden eindeutig bestimmt. Eine einfache Methode, die Parameter $c,d,r$ zu bestimmen, benutzt den Peripheriewinkelsatz für Kreise:

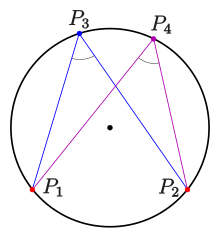
Vier Punkte $P_{i}=(x_{i},y_{i}),\ i=1,2,3,4$ (s. Bild) liegen genau dann auf einem Kreis, wenn die Winkel bei $P_{3}$ und $P_{4}$ gleich sind.

Üblicherweise misst man einen einbeschriebenen Winkel in Grad oder Radiant. Um die Gleichung eines Kreises durch 3 Punkte zu bestimmen, ist das folgende Winkelmaß geeigneter:

Um den Winkel zwischen zwei Geraden mit den Gleichungen $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2},\ m_{1}\neq m_{2}$ zu messen, wird hier der folgende Quotient benutzt:

${\frac {1+m_{1}\cdot m_{2}}{m_{2}-m_{1}}}$

Dieser Quotient ist der Kotangens des Schnittwinkels der beiden Geraden.

Peripheriewinkelsatz für Kreise:
Für vier Punkte $P_{i}=(x_{i},y_{i}),\ i=1,2,3,4$ keine drei auf einer Geraden (s. Bild) gilt:

Die vier Punkte liegen genau dann auf einem Kreis, wenn die Winkel bei $P_{3}$ und $P_{4}$ im obigen Winkelmaß gleich sind, d.h., wenn:

${\frac {(x_{4}-x_{1})(x_{4}-x_{2})+(y_{4}-y_{1})(y_{4}-y_{2})}{(y_{4}-y_{1})(x_{4}-x_{2})-(y_{4}-y_{2})(x_{4}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}$

Das Winkelmaß ist zunächst nur für Sekanten, die nicht parallel zur -Achse sind, verfügbar. Die angegebene vereinfachte Formel ist aber schließlich auch für diese Ausnahmen gültig.

Eine Folge des Peripheriewinkelsatzes in dieser Form ist:

3-Punkteform einer Kreisgleichung:

Die Gleichung des Kreises durch die 3 Punkte $P_{i}=(x_{i},y_{i})$ nicht auf einer Geraden ergibt sich durch Umformung der Gleichung (Beseitigung der Nenner und quadratische Ergänzung):

${\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}$

Diese Formel lässt sich durch Verwenden der Ortsvektoren, des Skalarproduktes und der Determinante übersichtlicher schreiben:

${\frac {({\color {red}{\vec {x}}}-{\vec {x}}_{1})\cdot ({\color {red}{\vec {x}}}-{\vec {x}}_{2})}{\det({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2})}}={\frac {({\vec {x}}_{3}-{\vec {x}}_{1})\cdot ({\vec {x}}_{3}-{\vec {x}}_{2})}{\det({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2})}}\;.$

Beispiel:

Für $P_{1}=(2,0),\;P_{2}=(0,1),\;P_{3}=(0,0)$ ergibt sich zunächst die 3-Punkteform

${\frac {(x-2)x+y(y-1)}{yx-(y-1)(x-2)}}=0$ und schließlich $(x-1)^{2}+(y-1/2)^{2}=5/4\ .$

Ellipsen

In diesem Abschnitt werden nur Ellipsen betrachtet mit Gleichungen

${\frac {(x-c)^{2}}{a^{2}}}+{\frac {(y-d)^{2}}{b^{2}}}=1\quad \leftrightarrow \quad (x-c)^{2}+{\frac {a^{2}}{b^{2}}}(y-d)^{2}=a^{2},\quad c,d,\in \mathbb {R} ,\ a>0\ ,$

für die der Quotient ${\tfrac {a^{2}}{b^{2}}}$ fest (invariant) ist. Mit der Abkürzung ${\color {blue}q}={\tfrac {a^{2}}{b^{2}}}$ erhält man die geeignetere Form

$(x-c)^{2}+{\color {blue}q}\;(y-d)^{2}=a^{2},\quad c,d\in \mathbb {R} ,\quad a>0$ und q>0

fest.

Die Achsen solcher Ellipsen sind parallel zu den Koordinatenachsen und ihre Exzentrizität (s. oben) ist fest. Die Hauptachse ist parallel zur -Achse, falls $q>1$ ist, und parallel zur -Achse, falls $q<1$ ist.

Ellipse: Peripheriewinkelsatz

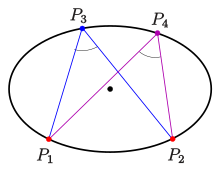
Wie beim Kreis ist so eine Ellipse durch drei Punkte nicht auf einer Geraden eindeutig bestimmt.

Für diesen allgemeineren Fall führt man das folgende Winkelmaß ein:

Um den Winkel zwischen zwei Geraden mit den Gleichungen $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2},\ m_{1}\neq m_{2}$ zu messen, wird hier der folgende Quotient benutzt:

${\frac {1+{\color {blue}q}\;m_{1}\cdot m_{2}}{m_{2}-m_{1}}}$

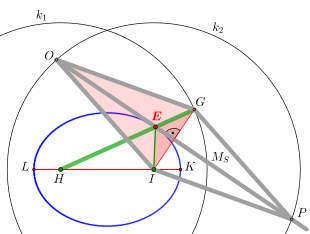
Peripheriewinkelsatz für Ellipsen:
Für vier Punkte $P_{i}=(x_{i},y_{i}),\ i=1,2,3,4$ keine drei auf einer Geraden (s. Bild) gilt:

Die vier Punkte liegen genau dann auf einer Ellipse mit der Gleichung $(x-c)^{2}+q\;(y-d)^{2}=a^{2}$ , wenn die Winkel bei $P_{3}$ und $P_{4}$ im obigen Winkelmaß gleich sind, d.h., wenn:

${\frac {(x_{4}-x_{1})(x_{4}-x_{2})+{\color {blue}q}\;(y_{4}-y_{1})(y_{4}-y_{2})}{(y_{4}-y_{1})(x_{4}-x_{2})-(y_{4}-y_{2})(x_{4}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+{\color {blue}q}\;(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}$

Das Winkelmaß ist zunächst nur für Sekanten, die nicht parallel zur -Achse sind, verfügbar. Die angegebene vereinfachte Formel ist aber schließlich auch für diese Ausnahmen gültig.

Der Beweis ergibt sich durch einfaches Nachrechnen. Dabei kann man im Fall „Punkte auf einer Ellipse …“ annehmen, dass der Mittelpunkt der Ellipse der Ursprung ist.

Eine Folge des Peripheriewinkelsatzes in dieser Form ist:

3-Punkteform einer Ellipsengleichung:
Die Gleichung der Ellipse durch die 3 Punkte $P_{i}=(x_{i},y_{i})$ nicht auf einer Geraden ergibt sich durch Umformung der Gleichung (Beseitigung der Nenner und quadratische Ergänzung):

${\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+{\color {blue}q}\;({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+{\color {blue}q}\;(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}$

Diese Formel lässt sich (wie beim Kreis) übersichtlicher darstellen durch

${\frac {({\color {red}{\vec {x}}}-{\vec {x}}_{1})*({\color {red}{\vec {x}}}-{\vec {x}}_{2})}{\det({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2})}}={\frac {({\vec {x}}_{3}-{\vec {x}}_{1})*({\vec {x}}_{3}-{\vec {x}}_{2})}{\det({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2})}}\;,$

wobei das hier geeignete Skalarprodukt ${\vec {u}}*{\vec {v}}=u_{x}v_{x}+{\color {blue}q}u_{y}v_{y}$ beschreibt.

Beispiel:

Für $P_{1}=(2,0),\;P_{2}=(0,1),\;P_{3}=(0,0)$ und $q=4$ ergibt sich zunächst die 3-Punkteform

${\frac {(x-2)x+4y(y-1)}{yx-(y-1)(x-2)}}=0$ und schließlich ${\frac {(x-1)^{2}}{2}}+{\frac {(y-1/2)^{2}}{1/2}}=1$ .

Ellipsen zeichnen

Würfel mit Kreisen in Vogelperspektive

Ellipsen treten in der darstellenden Geometrie als Bilder von Kreisen auf. Es ist also wichtig, geeignete Werkzeuge zur Verfügung zu haben, mit denen man Ellipsen zeichnen kann. Es gibt im Wesentlichen drei Typen von Verfahren, mit denen Ellipsen gezeichnet werden:

einzelne Punkte, die man mit einem Kurvenlineal zu einer glatten Kurve verbindet,
stetige Konstruktionen, die man technisch als Ellipsenzirkel realisieren kann und
eine Approximation einer Ellipse mit Hilfe ihrer Scheitelkrümmungskreise und eines Kurvenlineals.

Den meisten Ellipsenzirkeln liegen die unten beschriebenen zwei Papierstreifenmethoden zugrunde. Diese waren schon den Griechen (Archimedes und Proklos) bekannt. Wenn kein Ellipsenzirkel zur Verfügung steht, ist die Approximation mit Hilfe der Scheitelkrümmungskreise die schnellste und beste Methode, eine Ellipse zu zeichnen.

Für jede hier beschriebene Methode ist die Kenntnis der beiden (Symmetrie-)Achsen und der Halbachsen a,b erforderlich. Ist dies nicht der Fall, was in der darstellenden Geometrie oft vorkommt, so muss man wenigstens den Mittelpunkt und zwei konjugierte Halbmesser kennen. Mit Hilfe der Rytz-Konstruktion lassen sich dann die Scheitel und damit die Achsen und Halbachsen ermitteln. Nur die Parallelogramm-Methode (s. unten) bietet die Möglichkeit, zu zwei konjugierten Halbmessern direkt (ohne Rytz) einzelne Punkte einer Ellipse zu konstruieren.

Ellipse: Gärtnerkonstruktion

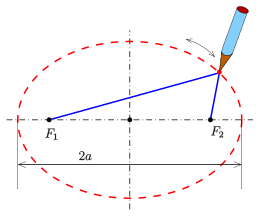
Gärtnerkonstruktion

Die definierende Eigenschaft einer Ellipse – die Summe der Abstände zu zwei Punkten ist konstant – nutzt die Gärtnerkonstruktion als einfache Möglichkeit, eine Ellipse zu zeichnen. Hierzu benötigt man einen Faden der Länge und zwei Reißbrettstifte (oder Nägel, Stifte, …), um die beiden Enden des Fadens in den Brennpunkten der zu zeichnenden Ellipse zu befestigen. Führt man einen Stift mit Hilfe des gespannten Fadens (s. Bild) über die Zeichenfläche, so entsteht die durch die Länge des Fadens und die Lage der Brennpunkte definierte Ellipse. Diese einfache Methode gibt Gärtnern die Möglichkeit, ellipsenförmige Beete anzulegen, was der Methode den Namen gab.

Eine Variation der Gärtnerkonstruktion zur Konstruktion konfokaler Ellipsen geht auf den irischen Bischof Charles Graves zurück.

Antiparallelogramm

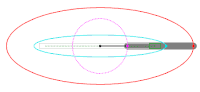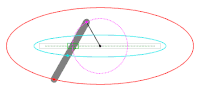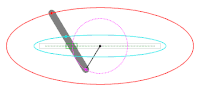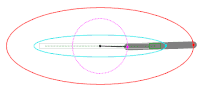
Konstruktion über das Antiparallelogramm

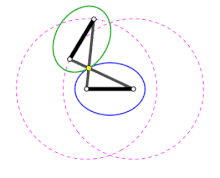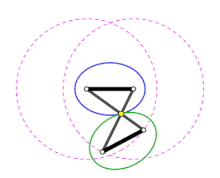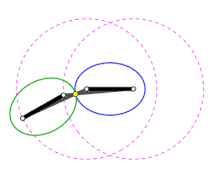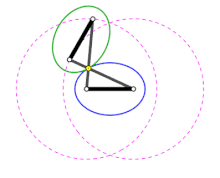
Beim Abrollen eines Antiparallelogramms zeichnet der Schnittpunkt der beiden langen Stäbe eine Ellipse (blau im Bild). Die Enden des kurzen statischen Stabs definieren die Brennpunkte der Ellipse. Durch die symmetrische Geometrie ergibt sich theoretisch auch um den kurzen umlaufende Stab eine Ellipse (im Bild grün). Diese Konstruktionsvariante ist mit der Gärtnerkonstruktion verwandt. Betrachtet man nur den Anteil innerhalb der statischen Ellipse und ersetzt die beiden inneren Teilstücke der Stäbe mit einer Schur ergibt sich die äquivalente Gärtnerkonstruktion. Die Mechanik des bewegten Antiparallelogramms ist ein Koppelgetriebe. Die innere Ellipse entspricht der Rastpolbahn die äußere Ellipse ist die Gangpolbahn des umlaufenden kurzen Stabs.

Ellipsenzirkel des Frans van Schooten

Ellipsenzirkel des Frans van Schooten

Im Jahr 1657 veröffentlichte Frans van Schooten in seinem Werk EXERCITATIONUM MATHEMATICARUM LIBRI QUINQUE in LIBER IV und ein paar Seiten weiter einen Ellipsenzirkel. Basis für den Ellipsenzirkel ist die Gärtnerkonstruktion.

Damit der Ellipsenzirkel eine komplette Ellipsenlinie zeichnen kann (auch durch die Scheitelpunkte und ), ist es erforderlich, dass zumindest einmal die Einstechposition der Zirkelnadeln und in den Brennpunkten der Ellipse getauscht wird, Anzumerken ist, in der nebenstehenden originären Darstellung Ellipsenzirkel des Frans van Schooten kann die Ellipsenlinie nicht durch den Scheitelpunkt gezogen werden, sondern nur, z. B. im Uhrzeigersinn, bis die Führungsschiene $|GH|$ an der Zirkelnadel in der Raute anliegt.

Prinzipskizze, Ellipsenzirkel des Frans van Schooten.
Die Kurve ist eine exakte Ellipse.

Die Hauptelemente des rautenförmigen Ellipsenzirkels sind die fünf gleich langen Stäbe mit ihren Gelenkpunkt-Abständen $|OI|$ , $|IP|$ , $|PG|$ , $|GO|$ und $|GH|$ , als Führungsschiene sowie der deutlich längere Diagonalstab ab durch mit dem Klemmelement für den Spielausgleich. Der Führungsschiene mit dem Gelenkpunkt-Abstand $|GH|$ und der Diagonalstab überkreuzen sich im Punkt und sind über Führungsnuten mithilfe eines sogenannten Gleitsteins dreh- und schiebbar verbunden. In diesem Gleitstein ist auch der Zeichenstift und ggf. der Handgriff montiert. Der zweite Gleitstein befindet sich im Gelenkpunkt . In den Gelenkpunkten und des Ellipsenzirkels sind die Zirkelnadeln befestigt.

Die Länge z.B. des Stabes $|IO|$ ist gleich der Länge der Hauptachse $|KL|$ . Der Abstand der Gelenkpunkte und bestimmt die Länge der Nebenachse. Je kleiner dieser Abstand ist, umso mehr ähnelt die Ellipse einem Kreis.

Betrachtet man eine Hälfte der Raute $OIPG$ , d.h. das gleichschenklige Dreieck $IGO$ , so ist der Diagonalstab ab durch als Mittelsenkrechte $M_{S}$ des Gelenkpunkt-Abstandes $|GI|$ erkennbar, die den Stab mit Gelenkpunkt-Abstand $|GH|$ in schneidet. Dadurch entsteht das zweite gleichschenklige Dreieck $EIG$ mit den Schenkeln $|EG|$ und $|EI|$ . Wird nun der Ellipsenzirkel von Hand bewegt, durchläuft der Punkt den Kreis $k_{1}$ um den Punkt mit dem Radius $|GH|$ (gleich $|KL|$ ), dabei wirkt der Diagonalstab mit seinem Gelenkpunkt-Abstand $|OP|$ konstant als Mittelsenkrechte der sich kontinuierlich verändernden gleichschenkligen Dreiecke $IGO$ und $EIG$ . Daraus folgt: In jeder gedrehten Stellung des Ellipsenzirkels gilt

$|GH|=|EH|+|EG|=|EH|+|EI|.$

Werden in die weiter oben beschriebene Definition einer Ellipse als geometrischer Ort die Bezeichnungen der betreffenden Punkte, u.a. die Brennpunkte und , aus der Darstellung des Ellipsenzirkels eingesetzt, ergibt sich

$Def_{E}=\{E\mid |EH|+|EI|=|GH|\}.$

Damit wird aufgezeigt: Die mit dem rautenförmigen Ellipsenzirkel gezogenen Kurven sind exakte Ellipsen.

Um eine Ellipse zu zeichnen, sticht man zuerst zur Lagefixierung des Ellipsenzirkels die Zirkelnadeln der Gelenkpunkte und in die Brennpunkte der Ellipse und zieht anschließend mithilfe des Handgriffs oder ggf. nur mit dem Zeichenstift die Ellipsenlinie.

Parameterdarstellung mit Sinus und Kosinus

Die übliche Parameterdarstellung einer Ellipse verwendet die Sinus- und Kosinusfunktion. Wegen $\cos ^{2}t+\sin ^{2}t=1$ beschreibt

$(a\cos t,b\sin t),\ 0\leq t<2\pi$

die Ellipse ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\ .$ Mit Hilfe dieser Darstellung lassen sich die folgenden Ellipsenkonstruktionen leicht verstehen.

Punktkonstruktion nach de La Hire

Die nach Philippe de La Hire (1640–1718) benannte Punktkonstruktion benutzt die beiden Scheitelkreise, das sind die Kreise um den Mittelpunkt der Ellipse mit den Halbachsen $a,\;b$ als Radien. Der Parameter wird hier als der Steigungswinkel eines von ausgehenden Strahls interpretiert. Mit der in der Zeichnung angegebenen Methode wird ein Punkt mit den Koordinaten $(a\cos t,b\sin t)$ , also ein Ellipsenpunkt, konstruiert. Dieses Konstruktionsverfahren war allerdings auch schon in der Spätantike bekannt und ging damals auf Proklos Diadochos (412–485) zurück.

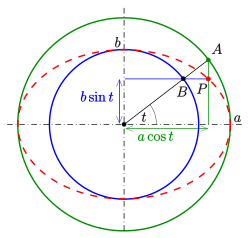Ellipsenkonstruktion nach Diadochos
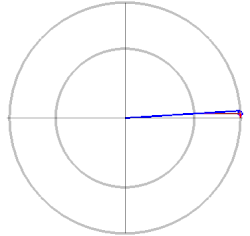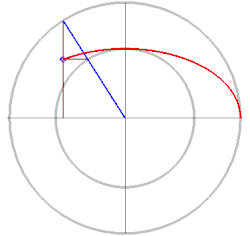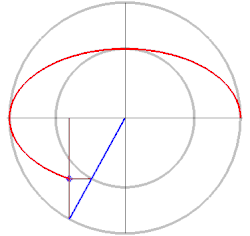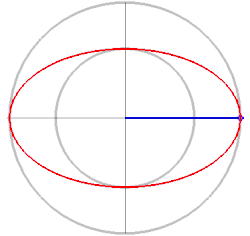Animation der Methode von Diadochos

Papierstreifenmethoden

Die beiden Papierstreifenmethoden verwenden zwei weitere Möglichkeiten der geometrischen Interpretation des Parameters der obigen Parameterdarstellung einer Ellipse. Sie liefern die Grundlagen der meisten Ellipsenzirkel.

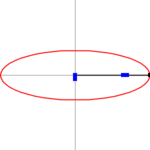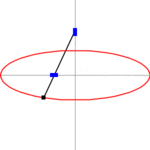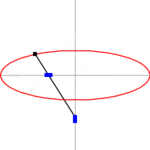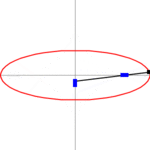
1. Methode

Die erste Methode verwendet einen Papierstreifen der Länge a+b . Der Punkt, in dem sich die Halbachsen treffen, wird mit markiert. Wenn der Streifen nun so bewegt wird, dass die beiden Enden jeweils auf einer Achse gleiten, überstreicht der Punkt die zu zeichnende Ellipse. Der Beweis ergibt sich aus der Parameterdarstellung $(a\cos t,\;b\sin t)$ und der Interpretation des Parameters als Winkel des Papierstreifens mit der -Achse (s. Bild).

Eine weitere technische Realisierung des gleitenden Streifens kann man auch mit Hilfe eines Paares cardanischer Kreise erreichen (s. Animation). Der große Kreis hat den Radius a+b .

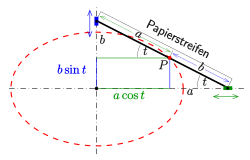Ellipse: 1. Papierstreifenmethode
Ellipsen (rot, cyan) mit cardanischen Kreisen

Eine Variation der 1. Papierstreifenmethode geht von der Beobachtung aus, dass der Mittelpunkt des Papierstreifens sich auf dem Kreis mit Mittelpunkt und Radius $\tfrac{a+b}{2}$ bewegt. Man kann also den Papierstreifen in der Mitte (Punkt ) trennen und an dieser Stelle ein Gelenk einfügen und den zuvor auf der -Achse gleitenden Punkt in den Mittelpunkt der Ellipse verlegen. Nach dieser Operation bleibt das abgeknickte Ende des Papierstreifens fest (im Punkt ) und der unveränderte Teil des Streifens samt dem Punkt bewegt sich wie zuvor. Der Vorteil dieser Variation ist: Man benötigt nur einen technisch anspruchsvollen Gleitschuh. Auch gegenüber der cardanischen Realisierung der 1. Papierstreifenmethode ist diese Variation technisch einfacher.
Man beachte, dass immer dasjenige Ende des Streifens, das auf der Nebenachse gleitet, in den Mittelpunkt verlegt wird!

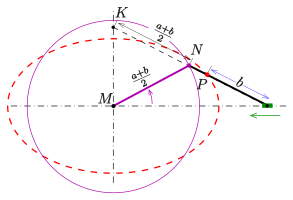Abgeknickter Papierstreifen
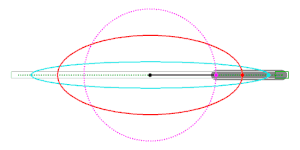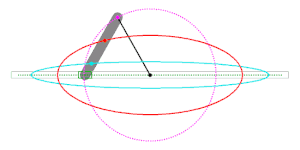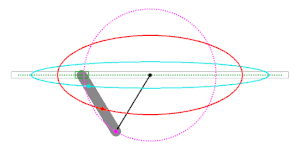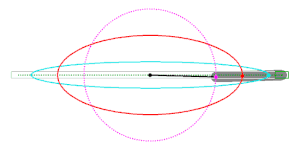Animation mit abgeknicktem Papierstreifen

Ellipse: 2. Papierstreifenmethode

2. Methode:

Die zweite Papierstreifenmethode geht von einem Papierstreifen der Länge aus. Man markiert den Punkt, der den Streifen in zwei Teile der Längen und a-b zerlegt. Der Streifen wird so auf den Achsen positioniert, wie im Bild zu sehen ist. Der Teil, der die Länge a-b besitzt, liegt zwischen den Achsen. Das freie Ende beschreibt dann die zu zeichnende Ellipse. Der Beweis ergibt sich aus der Zeichnung: Der Punkt kann durch die Parameterdarstellung $(a\cos t,\;b\sin t)$ beschrieben werden. Dabei ist der Steigungswinkel des Papierstreifens.

Diese Methode benötigt zu ihrer technischen Realisierung auch zwei Gleitschuhe, ist aber flexibler als die erste Papierstreifenmethode. Sie ist die Grundlage für viele Ellipsenzirkel.

Bemerkung: Auch hier ist eine Variation durch Abknicken des Streifenteils zwischen den Achsen möglich. Es ist dann, wie bei der ersten Methode, nur ein Gleitschuh nötig.

Animation der 2. Papierstreifenmethode
Ellipsenzirkel von Benjamin Bramer
Abgeknickter Papierstreifen

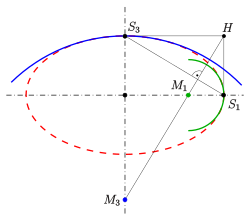
Approximation einer Ellipse mit Hilfe der Scheitelkrümmungskreise

Approximation mit Scheitelkrümmungskreisen

Aus der Formelsammlung (s. unten) ergibt sich:

Der Krümmungsradius für die Hauptscheitel $S_{1},\;S_{2}$ ist ${\tfrac {b^{2}}{a}}\ ,$

der Krümmungsradius für die Nebenscheitel $S_{3},\;S_{4}$ ist ${\tfrac {a^{2}}{b}}\ .$

Die Zeichnung zeigt eine einfache Methode, die Krümmungsmittelpunkte $M_{1}=(a-{\tfrac {b^{2}}{a}},0),\;M_{3}=(0,b-{\tfrac {a^{2}}{b}})$ des Scheitels $S_{1}$ und des Nebenscheitels $S_{3}$ zeichnerisch zu bestimmen:

Markiere den Hilfspunkt $H=(a,b)$ und zeichne die Gerade $S_{1}S_{3}$ .
Zeichne die Gerade durch , die senkrecht zur Geraden $S_{1}S_{3}$ verläuft.
Die Schnittpunkte $M_{1},\;M_{3}$ dieser Geraden mit den Ellipsenachsen sind die gesuchten Krümmungsmittelpunkte (Beweis: einfache Rechnung).

Die Krümmungsmittelpunkte der restlichen Scheitel ergeben sich aus Symmetrie. Man zeichnet die beiden restlichen Scheitelkrümmungskreise. Mit Hilfe eines Kurvenlineals lässt sich dann eine gute Näherung der Ellipse zeichnen.

Steiner-Erzeugung einer Ellipse (Parallelogramm-Methode)

Ellipse: Steiner-Erzeugung

Steiner-Erzeugung als Animation

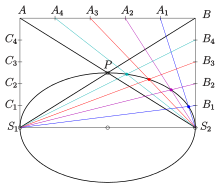
Die folgende Idee, einzelne Punkte einer Ellipse zu konstruieren, beruht auf der Steiner-Erzeugung eines Kegelschnitts (nach dem Schweizer Mathematiker Jakob Steiner):

Hat man für zwei Geradenbüschel in zwei Punkten $S_{1},\;S_{2}$ (alle Geraden durch den Punkt $S_{1}$ bzw. $S_{2}$ ) eine projektive, aber nicht perspektive Abbildung $\pi$ des einen Büschels auf das andere, so bilden die Schnittpunkte zugeordneter Geraden einen nichtausgearteten Kegelschnitt.

Für die Erzeugung einzelner Punkte der Ellipse $\tfrac{x^2}{a^2}+\tfrac{y^2}{b^2}=1$ gehen wir von den Geradenbüscheln in den Scheiteln $S_{1},\;S_{2}$ aus. Sei nun $P=(0,b)$ der obere Nebenscheitel der Ellipse und $A=(-a,2b),B=(a,2b)$ . Dann ist der Mittelpunkt des Rechtecks $S_{1},\;S_{2},\;B,\;A$ . Wir unterteilen die Rechteckseite ${\overline {AB}}$ in gleiche Stücke, übertragen diese Unterteilung mittels einer Parallelprojektion in Richtung der Diagonalen $AS_{2}$ auf die Strecke ${\overline {S_{2}B}}$ (s. Bild) und nummerieren die Unterteilungen wie im Bild. Die benutzte Parallelprojektion zusammen mit der Umkehrung der Orientierung vermittelt die nötige projektive Abbildung der Büschel in $S_{1}$ und $S_{2}$ . Die Schnittpunkte der zugeordneten Geraden $S_{1}B_{i}$ und $S_{2}A_{i}$ liegen dann auf der durch die Vorgaben (3 Punkte, 2 Tangenten) eindeutig bestimmten Ellipse. Mit Hilfe der Punkte $C_{1},\dotsc$ lassen sich Punkte auf dem 2. Viertel der Ellipse bestimmen. Analog erhält man Punkte der unteren Hälfte der Ellipse.

Bemerkung:
a) Benutzt man statt der Scheitel zwei Punkte eines anderen Durchmessers, so muss man für einen Punkt des konjugierten Durchmessers wählen und arbeitet dann mit einem Parallelogramm statt eines Rechtecks. Daher rührt auch der manchmal gebräuchliche Name Parallelogramm-Methode.
b) Den Beweis dieser Methode kann man auch am Einheitskreis nachrechnen. Da Teilverhältnisse und Parallelität bei affinen Abbildungen invariant bleiben, ist der Beweis dann auch allgemeingültig. (Eine Ellipse ist ein affines Bild des Einheitskreises!)

Auch für Parabel und Hyperbel gibt es Steiner-Erzeugungen.

Beispiele

Schaut man schräg auf einen Kreis (beispielsweise auf die Deckfläche eines Kreiszylinders), so erscheint dieser Kreis als Ellipse; präziser: Eine Parallelprojektion bildet Kreise im Allgemeinen auf Ellipsen ab.

In der Astronomie kommen Ellipsen häufig als Bahnen von Himmelskörpern vor. Nach dem ersten Keplerschen Gesetz bewegt sich jeder Planet auf einer Ellipse um die Sonne, wobei diese in einem der beiden Brennpunkte ruht. Entsprechendes gilt für die Bahnen von wiederkehrenden (periodischen) Kometen, Planetenmonden oder Doppelsternen. Allgemein ergeben sich bei jedem Zweikörperproblem der Gravitationskraft je nach Energie Ellipsen-, Parabel- oder Hyperbelbahnen.

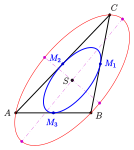Steiner-Inellipse (blau) mit Steiner-Ellipse (rot)
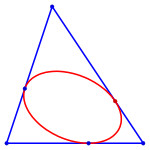
Beispiel einer Inellipse

Für jeden zwei- oder dreidimensionalen harmonischen Oszillator erfolgt die Bewegung auf einer Ellipsenbahn. So schwingt etwa der Pendelkörper eines Fadenpendels näherungsweise auf einer elliptischen Bahn, falls die Bewegung des Pendelfadens nicht nur in einer Ebene erfolgt.

In der Dreiecksgeometrie gibt es Steiner-Ellipsen Inellipsen (Steiner-Inellipse, Mandart-Ellipse).

Formelsammlung (Ellipsengleichungen)

Ellipsengleichung (kartesische Koordinaten)

Mittelpunkt (0|0) ,

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Aufgelöst nach $y^{2}$ :

$y^{2}=b^{2}\left(1-{\frac {x^{2}}{a^{2}}}\right)={\frac {(a^{2}-x^{2})(a^{2}-e^{2})}{a^{2}}}=(a^{2}-x^{2})(1-\varepsilon ^{2})$

Die letzte Form ist praktisch, um eine Ellipse mit Hilfe der beiden Bahnelemente, numerische Exzentrizität und große Halbachse, darzustellen.

Mittelpunkt $(x_{0}|y_{0})$ , Hauptachse parallel zur -Achse:

${\frac {(x-x_{0})^{2}}{a^{2}}}+{\frac {(y-y_{0})^{2}}{b^{2}}}=1.$

Ellipsengleichung (Parameterform)

Mittelpunkt (0|0) , Hauptachse als -Achse:

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}a\cos t\\b\sin t\end{pmatrix}}\quad {\text{mit}}\quad 0\leq t<2\pi .$

Mittelpunkt $(x_{0}|y_{0})$ , Hauptachse parallel zur -Achse:

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x_{0}+a\cos t\\y_{0}+b\sin t\end{pmatrix}}\quad {\text{mit}}\quad 0\leq t<2\pi .$

Mittelpunkt $(x_{0}|y_{0})$ , Hauptachse um $\alpha$ bezüglich -Achse rotiert:

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x_{0}+a\cos t\,\cos \alpha -b\sin t\,\sin \alpha \\y_{0}+a\cos t\,\sin \alpha +b\sin t\,\cos \alpha \end{pmatrix}}\quad {\text{mit}}\quad 0\leq t<2\pi .$

Dabei bezeichnet den Parameter dieser Darstellung. Dieser entspricht nicht dem Polarwinkel $\varphi$ zwischen der -Achse und der Geraden, die durch den Ursprung und den jeweiligen Ellipsenpunkt führt, sondern z.B. dem Polarwinkel zwischen der -Achse und der Geraden, die durch den Ursprung und den Punkt mit gleicher -Koordinate wie der Ellipsenpunkt jedoch auf dem Kreis mit Radius führt (vgl. Konstruktion nach de la Hire). In der Astronomie heißt dieser Parameter bei Keplerellipsen die exzentrische Anomalie, bei Meridianellipsen in der Geodäsie heißt er parametrische oder reduzierte Breite, vgl. Referenzellipsoid.

Für nicht rotierte Ellipsen, also $\alpha =0$ , hängt der Polarwinkel $\varphi$ , der durch $\tan \varphi =y/x$ definiert ist, mit dem Parameter zusammen über:

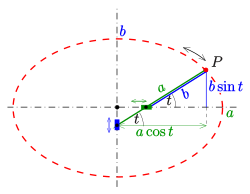
$\tan \varphi ={\frac {b}{a}}\tan t={\sqrt {1-\varepsilon ^{2}}}\,\tan t$

Diese Beziehung erlaubt eine anschauliche Interpretation des Parameters : Streckt man die -Koordinate eines Ellipsenpunktes P=(x,y) um den Faktor a/b , so liegt dieser neue Punkt P'=(x,y') auf einem Kreis mit Radius und demselben Mittelpunkt wie die Ellipse. Der Parameter ist nun der Winkel zwischen der -Achse und der Verbindungslinie ${\overline {MP'}}$ :

$y'={\frac {a}{b}}y=x{\frac {a}{b}}\tan \varphi =x\tan t=a\sin t\quad \Longrightarrow \quad {\begin{pmatrix}x\\y'\end{pmatrix}}=a{\begin{pmatrix}\cos t\\\sin t\end{pmatrix}}$

Ellipsengleichung (Polarkoordinaten bzgl. des Mittelpunkts)

Hauptachse waagrecht, Mittelpunkt als Pol, Polarachse längs Hauptachse nach rechts:

$r(\varphi )={\frac {ab}{\sqrt {a^{2}\sin ^{2}\varphi +b^{2}\cos ^{2}\varphi }}}={\frac {b}{\sqrt {1-\varepsilon ^{2}\cos ^{2}\varphi }}}\in [b,a]\quad {\text{mit}}\quad 0\leq \varphi <2\pi$

Exzentrische Anomalie

und wahre Anomalie $\varphi {\mathrm {R} }$ bzgl. des rechten Brennpunkts sowie wahre Anomalie $\varphi {\mathrm {L} }$ bzgl. des linken Brennpunkts als Funktion des Polarwinkels $\varphi$ für verschiedene numerische Exzentrizitäten $\varepsilon$

In kartesischen Koordinaten ausgedrückt, parametrisiert durch den Winkel der Polarkoordinaten, wobei der Mittelpunkt der Ellipse bei (0|0) und ihre Hauptachse entlang der -Achse liegt:

${\begin{pmatrix}x\\y\end{pmatrix}}={\frac {b}{\sqrt {1-\varepsilon ^{2}\cos ^{2}\varphi }}}{\begin{pmatrix}\cos \varphi \\\sin \varphi \end{pmatrix}}\quad {\text{mit}}\quad 0\leq \varphi <2\pi$

Herleitung

Aus der Ellipsengleichung in kartesischen Koordinaten $(x/a)^{2}+(y/b)^{2}=1$ und der Parametrisierung der kartesischen in Polarkoordinaten $x=r\cos \varphi$ und $y=r\sin \varphi$ folgt:

${\frac {r^{2}\cos ^{2}\varphi }{a^{2}}}+{\frac {r^{2}\sin ^{2}\varphi }{b^{2}}}=1\quad \Longrightarrow \quad r^{2}\left(b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi \right)=a^{2}b^{2}$

Umstellen und Radizieren liefert den Radius abhängig vom Polarwinkel.

Ellipsengleichung (Polarkoordinaten bzgl. eines Brennpunkts)

Hauptachse waagrecht, rechter Brennpunkt als Pol, Polarachse längs Hauptachse nach rechts (Halbparameter $p=b^{2}/a$ ):

$r_{\mathrm {R} }(\varphi _{\mathrm {R} })={\frac {a^{2}-e^{2}}{a+e\cos \varphi _{\mathrm {R} }}}={\frac {p}{1+\varepsilon \cos \varphi _{\mathrm {R} }}}\in [r_{\mathrm {peri} },r_{\mathrm {apo} }]\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {R} }<2\pi$

Hauptachse waagrecht, linker Brennpunkt als Pol, Polarachse längs Hauptachse nach rechts:

$r_{\mathrm {L} }(\varphi _{\mathrm {L} })={\frac {a^{2}-e^{2}}{a-e\cos \varphi _{\mathrm {L} }}}={\frac {p}{1-\varepsilon \cos \varphi _{\mathrm {L} }}}\in [r_{\mathrm {peri} },r_{\mathrm {apo} }]\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {L} }<2\pi$

Der Wertebereich der Radien erstreckt sich von der Periapsisdistanz $r_{\mathrm {peri} }$ bis zur Apoapsisdistanz $r_{\mathrm {apo} }$ , die folgende Werte haben:

$r_{\mathrm {peri} }={\frac {p}{1+\varepsilon }}=a(1-\varepsilon )\ ,\qquad r_{\mathrm {apo} }={\frac {p}{1-\varepsilon }}=a(1+\varepsilon )$

In kartesischen Koordinaten ausgedrückt, parametrisiert durch den Winkel $\varphi _{\mathrm {R} }$ bzw. $\varphi _{\mathrm {L} }$ der Polarkoordinaten, wobei der rechte Brennpunkt der Ellipse bei (e|0) , der linke Brennpunkt bei (-e|0) liegt:

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}e\\0\end{pmatrix}}+{\frac {p}{1+\varepsilon \cos \varphi _{\mathrm {R} }}}{\begin{pmatrix}\cos \varphi _{\mathrm {R} }\\\sin \varphi _{\mathrm {R} }\end{pmatrix}}\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {R} }<2\pi$

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}-e\\0\end{pmatrix}}+{\frac {p}{1-\varepsilon \cos \varphi _{\mathrm {L} }}}{\begin{pmatrix}\cos \varphi _{\mathrm {L} }\\\sin \varphi _{\mathrm {L} }\end{pmatrix}}\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {L} }<2\pi$

Der Winkel $\varphi _{\mathrm {R} }$ bzw. $\varphi _{\mathrm {L} }$ , je nachdem welcher Pol Bezugspunkt ist, heißt in der Astronomie die wahre Anomalie.

Herleitung

Man betrachtet ein Dreieck, das von den beiden Fixpunkten $F_{\mathrm {L} }$ , $F_{\mathrm {R} }$ und einem beliebigen Punkt auf der Ellipse aufgespannt wird.

Die Abstände zwischen diesen Punkten betragen: ${\overline {F_{\mathrm {L} }F_{\mathrm {R} }}}=2e$ sowie ${\overline {F_{\mathrm {L} }P}}=r_{\mathrm {L} }$ und nach der Definition der Ellipse ${\overline {F_{\mathrm {R} }P}}=2a-r_{\mathrm {L} }$ . Der Winkel bei $F_{\mathrm {L} }$ sei $\varphi _{\mathrm {L} }=\angle F_{\mathrm {R} }F_{\mathrm {L} }P$ . Mit dem Kosinussatz gilt nun:

$(2a-r_{\mathrm {L} })^{2}=(2e)^{2}+r_{\mathrm {L} }^{2}-2(2e)r_{\mathrm {L} }\cos \varphi _{\mathrm {L} }\quad \Longrightarrow \quad r_{\mathrm {L} }(a-\underbrace {e} _{a\varepsilon }\cos \varphi _{\mathrm {L} })=\underbrace {a^{2}-e^{2}} _{pa}$

Analog verläuft die Herleitung für den rechten Pol. Die Abstände lauten ${\overline {F_{\mathrm {L} }F_{\mathrm {R} }}}=2e$ und ${\overline {F_{\mathrm {R} }P}}=r_{\mathrm {R} }$ und ${\overline {F_{\mathrm {L} }P}}=2a-r_{\mathrm {R} }$ . Der Winkel bei $F_{\mathrm {R} }$ sei $\pi -\varphi _{\mathrm {R} }=\angle PF_{\mathrm {R} }F_{\mathrm {L} }$ , da $\varphi _{\mathrm {R} }=\angle (S_{\mathrm {R} },F_{\mathrm {R} },P)$ definiert ist, wobei $S_{\mathrm {R} }$ den rechten Hauptscheitel markiert.

$(2a-r_{\mathrm {R} })^{2}=(2e)^{2}+r_{\mathrm {R} }^{2}-2(2e)r_{\mathrm {R} }\underbrace {\cos(\pi -\varphi _{\mathrm {R} })} _{-\cos \varphi _{\mathrm {R} }}\quad \Longrightarrow \quad r_{\mathrm {R} }(a+\underbrace {e} _{a\varepsilon }\cos \varphi _{\mathrm {R} })=\underbrace {a^{2}-e^{2}} _{pa}$

Alternative Herleitung

Durch Gleichsetzen der zweier Darstellungen von $r_{\mathrm {L} }^{2}-r_{\mathrm {R} }^{2}$ erhält man:

$\left.{\begin{array}{l}r_{\mathrm {L} }^{2}-r_{\mathrm {R} }^{2}=\left[y^{2}+(x+e)^{2}\right]-\left[y^{2}+(x-e)^{2}\right]=4ex=4a\varepsilon x\\r_{\mathrm {L} }^{2}-r_{\mathrm {R} }^{2}=(r_{\mathrm {L} }+r_{\mathrm {R} })(r_{\mathrm {L} }-r_{\mathrm {R} })=2a(r_{\mathrm {L} }-r_{\mathrm {R} })\end{array}}\right\}\implies r_{\mathrm {L} }-r_{\mathrm {R} }=2\varepsilon x$

Dies entspricht einerseits mit $r_{\mathrm {R} }=2a-r_{\mathrm {L} }$ und $x=r_{\mathrm {L} }\cos \varphi _{\mathrm {L} }-e$

$2r_{\mathrm {L} }-2a=2\varepsilon (r_{\mathrm {L} }\cos \varphi _{\mathrm {L} }-e)\quad \Longrightarrow \quad r_{\mathrm {L} }(1-\varepsilon \cos \varphi _{\mathrm {L} })=a-\varepsilon e\equiv p$

und andererseits mit $r_{\mathrm {L} }=2a-r_{\mathrm {R} }$ und $x=r_{\mathrm {R} }\cos \varphi _{\mathrm {R} }+e$ :

$2a-2r_{\mathrm {R} }=2\varepsilon (r_{\mathrm {R} }\cos \varphi _{\mathrm {R} }+e)\quad \Longrightarrow \quad r_{\mathrm {R} }(1+\varepsilon \cos \varphi _{\mathrm {R} })=a-\varepsilon e\equiv p$

Formelsammlung (Kurveneigenschaften)

Tangentengleichung (kartesische Koordinaten)

Mittelpunkt (0|0) , Hauptachse als -Achse, Berührpunkt $(x_{B}|y_{B})$ :

${\frac {x_{B}x}{a^{2}}}+{\frac {y_{B}y}{b^{2}}}=1\quad \iff \quad {\frac {x_{B}(x-x_{B})}{a^{2}}}+{\frac {y_{B}(y-y_{B})}{b^{2}}}=0$

Mittelpunkt $(x_{0}|y_{0})$ Hauptachse parallel zur -Achse, Berührpunkt $(x_{B}|y_{B})$ :

${\frac {(x_{B}-x_{0})(x-x_{0})}{a^{2}}}+{\frac {(y_{B}-y_{0})(y-y_{0})}{b^{2}}}=1$

Tangentengleichung (Parameterform)

Ein (unnormierter) Tangentenvektor an die Ellipse hat die Gestalt:

${\vec {T}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}a\cos t\\b\sin t\end{pmatrix}}={\begin{pmatrix}-a\sin t\\b\cos t\end{pmatrix}}={\begin{pmatrix}-ay/b\\bx/a\end{pmatrix}}$

Die Tangentengleichung lautet in vektorieller Darstellung mit Mittelpunkt bei (0|0) , Hauptachse als -Achse und Berührpunkt bei $(x_{B}|y_{B})$ :

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x_{B}\\y_{B}\end{pmatrix}}+\mu {\begin{pmatrix}-ay_{B}/b\\bx_{B}/a\end{pmatrix}}\quad {\text{mit}}\quad \mu \in \mathbb {R}$

Beziehung zwischen Polar- und Normalenwinkel

Die Winkel der Ellipsentangente

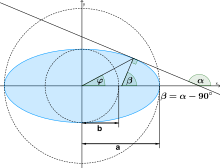
Zwischen Polarwinkel $\varphi$ und Normalenwinkel $\beta$ und Ellipsenparameter besteht folgender Zusammenhang (siehe nebenstehende Grafik)

$\tan \varphi ={\frac {b}{a}}\tan t={\frac {b^{2}}{a^{2}}}\tan \beta =(1-\varepsilon ^{2})\tan \beta$

Herleitung

Der Zusammenhang des Polarwinkels $\varphi$ und dem Steigungswinkel der Normalen $\beta$ (siehe Grafik rechts) lässt sich z.B. so finden:

Auflösen der Tangentengleichung nach

$y={\frac {b^{2}}{y_{B}}}-{\frac {b^{2}x_{B}}{a^{2}y_{B}}}x$

ergibt die Tangentensteigung $\tan(\alpha )=-\tan(\pi -\alpha )=\Delta y/\Delta x$ als Koeffizient von zu

$\tan \alpha =-{\frac {b^{2}}{a^{2}}}{\frac {x_{B}}{y_{B}}}=-{\frac {b^{2}}{a^{2}}}{\frac {1}{\tan \varphi }}.$

Mit $\tan \alpha =\tan(\beta +\pi /2)=-1/\tan \beta$ erhält man den gesuchten Zusammenhang zwischen $\beta$ und $\varphi$ .

Normalengleichung (kartesische Koordinaten)

Mittelpunkt (0|0) , Hauptachse als -Achse, Berührpunkt $(x_{B}|y_{B})$ :

$\left(1-{\frac {y}{y_{B}}}\right){\frac {b^{2}}{a^{2}}}+{\frac {x}{x_{B}}}=1$

oder auch

$b^{2}\left({\frac {y}{y_{B}}}-1\right)=a^{2}\left({\frac {x}{x_{B}}}-1\right)$

Normalengleichung (Parameterform)

Ein (unnormierter) Normalenvektor an die Ellipse hat die Gestalt:

${\vec {N}}={\begin{pmatrix}b\cos t\\a\sin t\end{pmatrix}}={\begin{pmatrix}bx/a\\ay/b\end{pmatrix}}$

Die Normalengleichung lautet in vektorieller Darstellung mit Mittelpunkt bei (0|0) , Hauptachse als -Achse und Berührpunkt bei $(x_{B}|y_{B})$ :

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x_{B}\\y_{B}\end{pmatrix}}+\mu {\begin{pmatrix}bx_{B}/a\\ay_{B}/b\end{pmatrix}}\quad {\text{mit}}\quad \mu \in \mathbb {R}$

Krümmungsradien und -mittelpunkte

Krümmungsradius im Punkt $(x_{p}|y_{p})$ :

$r=a^{2}b^{2}\left({\frac {x_{p}^{2}}{a^{4}}}+{\frac {y_{p}^{2}}{b^{4}}}\right)^{3/2}={\frac {1}{a^{4}b^{4}}}{\sqrt {\left(a^{4}y_{p}^{2}+b^{4}x_{p}^{2}\right)^{3}}}$

Mittelpunkt des Krümmungskreises, Krümmungsmittelpunkt $M(\xi |\eta )$ :

$\xi ={\frac {e^{2}x_{p}^{3}}{a^{4}}}\qquad \eta =-{\frac {e^{2}y_{p}^{3}}{b^{4}}}\qquad \vert \,e^{2}=a^{2}\varepsilon ^{2}=a^{2}-b^{2}$ /DD>

Krümmungsradius und -mittelpunkt in einem der beiden Hauptscheitel $(\pm a|0)$ :

$r_{\mathrm {H} }={\frac {b^{2}}{a}}\qquad M_{\mathrm {H} }\left(\xi =\pm {\frac {e^{2}}{a}}\,{\bigg |}\,\eta =0\right)$

Krümmungsradius und -mittelpunkt in einem der beiden Nebenscheitel $(0|\pm b)$ :

$r_{\mathrm {N} }={\frac {a^{2}}{b}}\qquad M_{\mathrm {N} }\left(\xi =0\,{\bigg |}\,\eta =\pm {\frac {e^{2}}{b}}\right)$

Formelsammlung (Flächeninhalt und Umfang)

Flächeninhalt

Mit den Halbachsen und :

$A=\pi ab=\pi a^{2}{\sqrt {1-\varepsilon ^{2}}}$

Ist die Ellipse durch eine implizite Gleichung

$\alpha x^{2}+\beta xy+\gamma y^{2}+1=0$

gegeben, dann beträgt ihr Flächeninhalt

$A={\frac {2\pi }{\sqrt {4\alpha \gamma -\beta ^{2}}}}.$

Ellipsensektor

Für eine Ellipse mit den Halbachsen und und einen Sektor, der mit der großen Halbachse den Winkel $\varphi \in \left]0,{\frac {\pi }{2}}\right[$ einschließt, gilt:

$A_{\mathrm {Sektor} }={\frac {ab}{2}}\arctan \left({\frac {a}{b}}\tan(\varphi )\right)$

Beschreibt man den Ellipsensektor statt durch den Polarwinkel durch den Parameter aus der Parameterdarstellung $(x,y)=(a\cos t,b\sin t)$ , so erhält man die Formel

$A_{\mathrm {Sektor} }={\frac {ab}{2}}t.$

Umfang

Formel

Der Umfang einer Ellipse mit großer Halbachse und kleiner Halbachse berechnet sich zu

$U=4a\cdot E(\varepsilon )$ ,

wobei E(k) für das vollständige elliptische Integral zweiter Art steht. Die numerische Exzentrizität $\varepsilon$ berechnet sich bei Ellipsen als

$\varepsilon ={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$ .

Diagramm zur Berechnung des Ellipsenumfangs $U=k\cdot a$ mit $k=4E(\varepsilon )$

Herleitung

Ellipsen mit gleichem Umfang

Der Umfang einer Ellipse kann nicht exakt durch elementare Funktionen ausgedrückt werden. Er kann aber mithilfe eines Integral dargestellt werden, das daher elliptisches Integral genannt wird.

Die Formel für die Bogenlänge einer Kurve ${\mathcal {C}}$ lautet

$L=\int \limits _{\mathcal {C}}|\gamma '(t)|\;\mathrm {d} t$ .

Für die Ellipse mit der Parameterdarstellung $\;(a\cos t,b\sin t),\;0\leq t\;<2\pi ,\;$ ergibt sich unter Berücksichtigung der Symmetrie für den Umfang

$U=4\int _{0}^{\pi /2}{\sqrt {a^{2}\cdot \sin ^{2}t+b^{2}\cdot \cos ^{2}t}}\;\mathrm {d} t$ .

Ausklammern von $a^{2}$ , Verwendung von $\;\sin ^{2}t=1-\cos ^{2}t\;$ und $\;\varepsilon ^{2}=1-{\frac {b^{2}}{a^{2}}}\;$ führt zu

$U=4a\cdot \int _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}\cdot \cos ^{2}t}}\;\mathrm {d} t\ .$

Durch die Substitution $\vartheta ={\frac {\pi }{2}}-t,\;\mathrm {d} t=-\mathrm {d} \vartheta$ erhalten wir die folgende Form:

$E(\varepsilon )=\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}\cdot \sin ^{2}\vartheta }}\;\mathrm {d} \vartheta$ .

Das Integral $E(\varepsilon )$ nennt man vollständiges elliptisches Integral zweiter Art.

Der Umfang der Ellipse ist damit

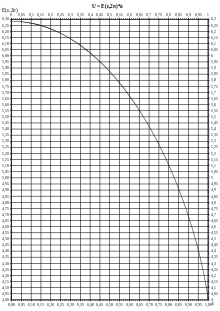
$U=4a\cdot E(\varepsilon ),\quad \varepsilon ={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$ .

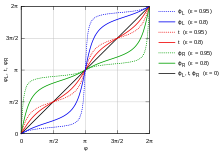
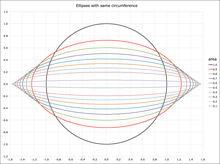
Der Umfang hängt also von der numerischen Exzentrizität $\varepsilon$ und der großen Halbachse ab. Mithilfe des nebenstehenden Diagramms kann bei gegebener Exzentrizität $\varepsilon$ der Wert des Faktors $k=4E(\varepsilon )$ für den Umfang $U=k\cdot a$ abgelesen werden. liegt für jede Ellipse zwischen den Extremfällen k=4 ( $\varepsilon =1$ , entartete Ellipse als Linie) und $k=2\pi$ ( $\varepsilon =0$ , Ellipse wird zum Kreis).

Reihenentwicklung

${\begin{aligned}U&=2a\pi \left(1-\sum _{i=1}^{\infty }\left(\prod _{j=1}^{i}{\frac {2j-1}{2j}}\right)^{2}{\frac {\varepsilon ^{2i}}{2i-1}}\right)\\&=2a\pi \left[1-\left({\frac {1}{2}}\right)^{2}\varepsilon ^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {\varepsilon ^{4}}{3}}-\ldots -\left({\frac {1\cdot 3\cdot 5\dotsm (2n-1)}{2\cdot 4\cdot 6\dotsm 2n}}\right)^{2}{\frac {\varepsilon ^{2n}}{2n-1}}-\ldots \right]\end{aligned}}$

Für $\varepsilon$ nahe 1 konvergiert diese Reihenentwicklung extrem langsam. Es empfiehlt sich daher eine numerische Integration, z.B. nach dem Romberg-Verfahren.

Eine Reihe, die schneller konvergiert, beruht auf der Gauß-Kummer-Reihe. Für eine Ellipse mit den Halbachsen und (mit a>b ) wird $\lambda ={\tfrac {a-b}{a+b}}$ definiert. Dann ergibt sich:

${\begin{aligned}U&=\pi (a+b)\left(1+\sum _{n=0}^{\infty }\left({\frac {\binom {2n}{n}}{(n+1)2^{2n+1}}}\right)^{2}\ \lambda ^{2n+2}\right)\\&=\pi (a+b)\left(1+{\frac {\lambda ^{2}}{4}}+{\frac {\lambda ^{4}}{64}}+{\frac {\lambda ^{6}}{256}}\ +{\frac {25\lambda ^{8}}{16\,384}}+{\frac {49\lambda ^{10}}{65\,536}}+{\frac {441\lambda ^{12}}{1\,048\,576}}+{\frac {1\,089\lambda ^{14}}{4\,194\,304}}+\dotsb +\ \left({\frac {1\cdot 3\cdot 5\dotsm (2n-1)}{2\cdot 4\cdot 6\cdot 8\dotsb (2n+2)}}\right)^{2}\lambda ^{2n+2}+\dotsb \right)\end{aligned}}$

Näherungen

Näherung mit Hilfe des arithmetischen Mittels der Halbachsen

$U\approx \pi (a+b)$

Genauigkeit dieser Formel

Exz. ε	q = b / a	Fehler
= 0,000	1,000	0 (Kreis: exakt)
< 0,051	> 0,9987	< 10⁻⁷
< 0,090	> 0,996	< 10⁻⁶
< 0,1582	> 0,9874	< 10⁻⁵
< 0,277	> 0,961	< 0,01 %
< 0,46	> 0,885	< 0,1 %
< 0,75	> 0,66	< 1 %
< 0,83	> 0,55	< 2 %
< 0,927	> 0,37	< 5 %
< 0,978	> 0,21	< 10 %
< 0,999	> 0,044	< 18,3 %
< 1,000	> 0,000	< 21,46 %

Näherung mit Hilfe des quadratischen Mittels der Halbachsen

$U\approx 2\pi {\sqrt {{\frac {1}{2}}(a^{2}+b^{2})}}=\pi {\sqrt {2(a^{2}+b^{2})}}$

$U\approx 2\pi {\sqrt {{\frac {1}{2}}(a^{2}+a^{2}(1-\epsilon ^{2}))}}=2\pi a{\sqrt {1-{\frac {\epsilon ^{2}}{2}}}}$

Genauigkeit dieser Formel

Exz. ε	q = b / a	Fehler
= 0,000	= 1,0000	0 (Kreis: exakt)
< 0,016	> 0,9999	< 10⁻⁹
< 0,026	> 0,9997	< 10⁻⁸
< 0,047	> 0,9989	< 10⁻⁷
< 0,084	> 0,9965	< 10⁻⁶
< 0,149	> 0,9888	< 10⁻⁵
< 0,262	> 0,9651	< 0,01 %
< 0,450	> 0,8930	< 0,1 %
< 0,720	> 0,6937	< 1 %
< 0,808	> 0,5891	< 2 %
< 0,914	> 0,4037	< 5 %
< 0,977	> 0,2104	< 10 %
< 1,000	> 0,0000	< 14,91 %

Näherungsformel nach Ramanujan

$U\approx \pi \left((a+b)\,+\,{\frac {3(a-b)^{2}}{10(a+b)+{\sqrt {a^{2}+14ab+b^{2}}}}}\right)$

bzw.

$U\approx \pi (a+b)\left(1+{\frac {3\lambda ^{2}}{10+{\sqrt {4-3\lambda ^{2}}}}}\right)$ , wobei $\quad \lambda ={\frac {a-b}{a+b}}$ .

Diese Näherung ist in einem weiten $\varepsilon$ -Bereich von $0\leq \varepsilon \leq 0{,}9$ sehr genau und ergibt im gesamten Bereich stets einen etwas zu kleinen Wert, der monoton mit $\varepsilon$ zunimmt.

Der relative Fehler beträgt:

Bereich	rel. Fehler
0,0000 ≤ ε ≤ 0,8820	< 10⁻⁹
0,8820 < ε ≤ 0,9242	< 10⁻⁸
0,9242 < ε ≤ 0,9577	< 10⁻⁷
0,9577 < ε ≤ 0,9812	< 10⁻⁶
0,9812 < ε ≤ 0,9944	< 10⁻⁵
0,9944 < ε ≤ 0,9995	< 10⁻⁴
0,9995 < ε ≤ 1,0000	< 0,000403

Für $\varepsilon =\lambda =1$ erhält man statt 4 den minimal zu kleinen Wert ${\tfrac {14}{11}}\pi$ .

Siehe auch: Meridianbogen

Siehe auch

Steiner-Ellipse
Konfokale Kegelschnitte
Ellipsoid
Der Rotationskörper mit einem elliptischen Querschnitt ist ein Rotationsellipsoid.
Fokaloid

Basierend auf einem Artikel in:

Wikipedia.de