Kosinussatz

Der Kosinussatz ist einer der fundamentalen Lehrsätze der Geometrie und hier dem Gebiet der Trigonometrie zugehörig. Er ist eng verwandt mit dem Satz des Pythagoras.

Für ebene Dreiecke ist der Kosinussatz sehr einfach zu formulieren, für sphärische benötigt er sechs Winkelfunktionen. In beiden Fällen beinhaltet er drei Identitätsgleichungen, welche die Beziehungen zwischen den Längen der Seiten von Dreiecken und den Kosinuswerten ihrer Winkel darstellen.

Kosinussatz für ebene Dreiecke

Allgemeine Formulierung

Bezeichnungen im Dreieck

Für die drei Seiten , und eines Dreiecks sowie für den der Seite gegenüberliegenden Winkel (d.h. den zwischen den Seiten und liegenden Winkel) $\gamma$ gilt:

$c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma$

Umkehrung für den Winkel:

$\cos \gamma ={\frac {a^{2}+b^{2}-c^{2}}{2\cdot a\cdot b}}$

Entsprechend gilt für die anderen Winkel:

$b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos \beta$

$a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos \alpha$

Gleichwertige Formulierung

Die zuvor genannten drei Identitätsgleichungen sind ihrerseits Folgerungen aus den folgenden drei Kosinusformeln und im Rahmen der Trigonometrie der euklidischen Ebene sogar gleichwertig mit

$a=b\cdot \cos \gamma +c\cdot \cos \beta$

$b=c\cdot \cos \alpha +a\cdot \cos \gamma$

$c=a\cdot \cos \beta +b\cdot \cos \alpha$

Man fasst diese Formeln unter dem Stichwort Projektionssatz oder Projektionssätze zusammen.

Der Satz des Pythagoras als Spezialfall des Kosinussatzes

Mit $\textstyle \gamma =90^{\circ }={\frac {\pi }{2}}$ , also bei einem rechtwinkligen Dreieck, gilt $\textstyle \cos \gamma =\cos {\frac {\pi }{2}}=0$ . Dadurch ergibt sich als Spezialfall des Kosinussatzes im rechtwinkligen Dreieck der Satz des Pythagoras:

Der Kosinussatz stellt daher eine Verallgemeinerung des Satzes von Pythagoras dar und wird auch erweiterter Satz des Pythagoras genannt.

Kosinussatz für Kugeldreiecke

Beim sphärischen Kosinussatz für Kugeldreiecke ist die Länge der Dreiecksseiten im Winkelmaß anzugeben, weshalb statt einer Winkelfunktion deren sechs auftreten. Das Analogon zum ebenen Satz

$c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma$

lautet daher

$\cos c=\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma$ ,

wobei die Umkehr des Vorzeichens zu beachten ist. Diesem Seiten-Kosinussatz (hier für c, analog für die Seiten a bzw. b) steht der Winkel-Kosinussatz gegenüber:

$\cos \gamma =-\cos \alpha \cdot \cos \beta +\sin \alpha \cdot \sin \beta \cdot \cos c$ ,

worin das erste Vorzeichen negativ ist.

Anwendungen

Zahlenbeispiel

In einem Dreieck ABC sind folgende Seitengrößen bekannt (Bezeichnungen wie üblich):

$a=4{,}00\;{\rm {cm}}$

$b=2{,}00\;{\rm {cm}}$

$c=3{,}70\;{\rm {cm}}$

Gesucht ist die Winkelgröße $\beta$ (Bezeichnungen wie üblich).

$b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos \beta$

$2\cdot a\cdot c\cdot \cos \beta =a^{2}+c^{2}-b^{2}$

$\cos \beta \,=\,{\frac {a^{2}+c^{2}-b^{2}}{2\cdot a\cdot c}}={\frac {(4{,}0\,{\rm {cm}})^{2}+(3{,}7\,{\rm {cm}})^{2}-(2{,}0\,{\rm {cm}})^{2}}{2\cdot 4{,}0\,{\rm {cm}}\cdot 3{,}7\,{\rm {cm}}}}=0{,}868$

$\beta =29{,}8^{\circ }$

Kongruenzsätze

Die Kongruenzsätze SSS und SWS besagen, dass ein Dreieck durch die Vorgabe von drei Seiten oder von zwei Seiten und ihrem Zwischenwinkel vollständig bestimmt ist. Alternativ kann man auch jeweils zwei Vektoren angeben, aus denen der eingeschlossene Winkel berechnet werden kann. Der Kosinussatz erlaubt es in diesen Fällen, aus den drei gegebenen Stücken ein viertes Stück, nämlich einen Winkel (im Fall SSS) beziehungsweise die dritte Seite (im Fall SWS) zu berechnen. Wenn man anschließend auch die übrigen Winkel eines Dreiecks ermitteln möchte, kann man wahlweise nochmal den Kosinussatz (mit auf den gesuchten Winkel angepassten Seitenbezeichnungen) oder den Sinussatz anwenden. Den letzten Winkel berechnet man am zweckmäßigsten über die Winkelsumme von 180°.

Wenn nur eine Seite und zwei Winkel gegeben sind (Kongruenzsätze SWW oder WSW) oder zwei Seiten und der Gegenwinkel der größeren Seite (Kongruenzsatz SsW), so berechnet man zunächst eines der fehlenden Stücke mit dem Sinussatz und den fehlenden Winkel über die Winkelsumme, bevor man mit dem Kosinussatz die dritte Seite bestimmen kann.

Verallgemeinerung

Mit Vektoren in reellen Skalarprodukträumen, also Vektorräumen mit Skalarprodukt $\langle \cdot ,\cdot \rangle$ , kann auch der Kosinussatz leicht verallgemeinert werden. Bezeichnet

$\|a\|={\sqrt {\langle a,a\rangle }}$

die Skalarproduktnorm, also die Länge, eines Vektors $a\in V$ und $\theta _{a,b}$ mit

$\cos \theta _{a,b}={\frac {\langle a,b\rangle }{\|a\|\cdot \|b\|}}$

den Winkel zwischen den beiden Vektoren $a,b\in V$ , dann gilt für die Norm des Vektors c=b-a :

${\begin{aligned}\|c\|^{2}&=\|b-a\|^{2}=\langle b-a,b-a\rangle =\langle b,b\rangle -\langle b,a\rangle -\langle a,b\rangle +\langle a,a\rangle \\&=\|a\|^{2}+\|b\|^{2}-2\cdot \langle a,b\rangle =\|a\|^{2}+\|b\|^{2}-2\cdot \|a\|\cdot \|b\|\cos \theta _{a,b}\end{aligned}}$

Beweis

Elementargeometrischer Beweis

Im folgenden Beweis wird $\gamma <90^{\circ }$ vorausgesetzt. Für $\gamma >90^{\circ }$ muss der Beweis geringfügig modifiziert werden. Für $\gamma =90^{\circ }$ ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.

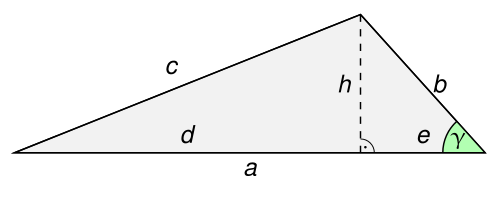
In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für $c^{2}$ zu finden. Dazu benötigt man die Quadrate der Kathetenlängen dieses Teildreiecks:

$h^{2}\,=b^{2}-e^{2}$ (Satz des Pythagoras für das rechte Teildreieck)

$d^{2}=(a-e)^{2}=a^{2}-2\cdot a\cdot e+e^{2}$ (binomische Formel)

Nach Pythagoras gilt für das linke Teildreieck:

$c^{2}\,=h^{2}+d^{2}$

Es müssen also die beiden oben gefundenen Rechenausdrücke addiert werden:

$c^{2}=b^{2}-e^{2}+a^{2}-2\cdot a\cdot e+e^{2}=a^{2}+b^{2}-2\cdot a\cdot e$

Zusätzlich gilt

$\cos \gamma ={\frac {e}{b}}$

mit der Folgerung

$e=b\cdot \cos \gamma$ .

Einsetzen dieses Zwischenergebnisses in die Gleichung für $c^{2}$ ergibt die Behauptung:

$c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma$

Trigonometrischer Beweis

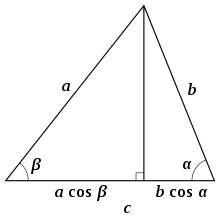
Zeichnet man das Lot auf der Seite ein, dann wird diese in zwei Abschnitte geteilt und es gilt:

$c=a\cdot \cos \beta +b\cdot \cos \alpha$

Multiplikation mit ergibt

$c^{2}=a\cdot c\cdot \cos \beta +b\cdot c\cdot \cos \alpha$

Analog erhält man für die beiden anderen Seiten die Gleichungen

$a^{2}=a\cdot c\cdot \cos \beta +a\cdot b\cdot \cos \gamma$

$b^{2}=b\cdot c\cdot \cos \alpha +a\cdot b\cdot \cos \gamma$

Addiert man diese beiden Gleichungen, dann folgt daraus

$a^{2}+b^{2}=a\cdot c\cdot \cos \beta +b\cdot c\cdot \cos \alpha +2\cdot a\cdot b\cdot \cos \gamma$

$a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma =a\cdot c\cdot \cos \beta +b\cdot c\cdot \cos \alpha$

Weil die rechte Seite der letzten Gleichung und die rechte Seite von $c^{2}=a\cdot c\cdot \cos \beta +b\cdot c\cdot \cos \alpha$ übereinstimmen, kann man die beiden linken Seiten gleichsetzen:

$c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma$

Beweis mittels Vektorrechnung

Anschließend an die Darstellung von Gericke und Raith wird zunächst der Beweis der drei Kosinusformeln geführt:^[1]

Dazu macht man die Festlegungen

${\vec {a}}={\overrightarrow {BC}},\quad {\vec {b}}={\overrightarrow {CA}},\quad {\vec {c}}={\overrightarrow {AB}}$ .

Man erhält daraus die Gleichungen

$-{\vec {a}}={\overrightarrow {CB}},\quad -{\vec {b}}={\overrightarrow {AC}},\quad -{\vec {c}}={\overrightarrow {BA}}$

sowie unter Benutzung der Eigenschaften des Skalarprodukts

$a=|{\vec {a}}|=|{-{\vec {a}}}|,\quad b=|{\vec {b}}|=|{-{\vec {b}}}|,\quad c=|{\vec {c}}|=|{-{\vec {c}}}|$

und

$\cos \alpha ={\frac {\langle -{\vec {b}},{\vec {c}}\rangle }{|{-{\vec {b}}}|\cdot |{\vec {c}}|}}={\frac {\langle -{\vec {b}},{\vec {c}}\rangle }{b\cdot c}},\quad \cos \beta ={\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{|{-{\vec {c}}}|\cdot |{\vec {a}}|}}={\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{c\cdot a}},\quad \cos \gamma ={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{|{-{\vec {a}}}|\cdot |{\vec {b}}|}}={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{a\cdot b}}$ .^[2]

Nun zieht man die für das Dreieck charakteristische Grundgleichung

${\vec {a}}+{\vec {b}}+{\vec {c}}={\vec {0}}$

heran und gewinnt

${\vec {a}}=(-{\vec {b}})+(-{\vec {c}})$

und weiter

$a^{2}=|{\vec {a}}|^{2}=\langle {\vec {a}},{\vec {a}}\rangle =\langle -{\vec {b}},{\vec {a}}\rangle +\langle -{\vec {c}},{\vec {a}}\rangle$ .

Folglich ergibt sich

$a={\frac {\langle -{\vec {b}},{\vec {a}}\rangle }{a}}+{\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{a}}={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{a}}+{\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{a}}=b\cdot \cos \gamma +c\cdot \cos \beta$

und damit die erste der obigen drei Kosinusformeln.

Die beiden anderen erhält man auf gleiche Art und Weise.

Auf die drei Formeln der allgemeinen Formulierung kann man dann mittels elementarer algebraischer Operationen schließen. So erhält man die erste Gleichung, indem man die zuvor stehenden drei Kosinusformeln nacheinander mit , und multipliziert, aufaddiert und nach $c^{2}$ auflöst.

Siehe auch

Anmerkungen

↑ Der Beweis des Projektionssatzes lässt sich auch, und zwar in ähnlicher Weise wie der vorangehende Beweis, im Rahmen der Elementargeometrie führen.
↑ Es soll o.B.d.A. vorausgesetzt sein, dass ein nicht-ausgeartetes Dreieck vorliegt, also keine der drei Seiten und damit auch keiner der drei Vektoren die Länge $0$ hat.

Basierend auf einem Artikel in:

Wikipedia.de