Skalarproduktnorm

Eine Skalarproduktnorm, Innenproduktnorm oder Hilbertnorm ist in der Mathematik eine von einem Skalarprodukt induzierte (abgeleitete) Norm. In einem endlichdimensionalen reellen oder komplexen Vektorraum mit dem Standardskalarprodukt entspricht die Skalarproduktnorm gerade der euklidischen Norm. Allgemein besitzt jeder Prähilbertraum eine zugeordnete Skalarproduktnorm und ist mit dieser Norm ein normierter Raum. Eine Norm ist dabei genau dann von einem Skalarprodukt induziert, wenn sie die Parallelogrammgleichung erfüllt. Jede Skalarproduktnorm erfüllt weiterhin die Cauchy-Schwarz-Ungleichung und ist invariant unter unitären Transformationen.

Definition

Beziehungen zwischen Skalarprodukt, Norm und Metrik

Ist ein Vektorraum über den Körper ${\mathbb K}$ der reellen oder komplexen Zahlen und $\langle \cdot ,\cdot \rangle$ ein Skalarprodukt auf $V \times V$ , dann ist $( V, \langle \cdot , \cdot \rangle )$ ein Skalarproduktraum. Die von diesem Skalarprodukt induzierte Norm ist für einen Vektor $v\in V$ dann definiert als

$\| v \| := \sqrt{\langle v, v\rangle}$ ,

also die Wurzel aus dem Skalarprodukt des Vektors mit sich selbst. Diese Definition ist wohldefiniert, da das Skalarprodukt eines Vektors mit sich selbst reell und nichtnegativ ist.

Diese Norm heißt auch Skalarproduktnorm, Innenproduktnorm oder Hilbertnorm und wird in reellen Skalarprodukträumen gelegentlich als (allgemeine) euklidische Norm bezeichnet. Mit der Skalarproduktnorm ist der Vektorraum ein normierter Raum $(V,\|\cdot \|)$ . Weiterhin ist mit der von der Norm induzierten Metrik ein metrischer Raum (V, d) und mit der Normtopologie $\mathcal T$ ein topologischer Raum $(V, {\mathcal T})$ .

Beispiele

Wichtige Beispiele für Skalarproduktnormen sind:

die euklidische Norm auf dem euklidischen Raum der endlichdimensionalen Vektoren,
die ℓ²-Norm auf dem Raum ℓ² der quadratisch summierbaren Folgen,
die L²-Norm auf dem Raum L² der quadratisch Lebesgue-integrierbaren Funktionen,
die Sobolev-Norm auf dem Sobolev-Raum H^s der Funktionen, deren gemischte schwache Ableitungen bis zum Grad quadratisch Lebesgue-integrierbar sind,
die Frobeniusnorm auf dem Raum der Matrizen,
die Hilbert-Schmidt-Norm auf dem Raum der Hilbert-Schmidt-Operatoren.

Eigenschaften

Die durch das Skalarprodukt induzierte Abbildung $\| v \| := \sqrt{\langle v, v\rangle}$ ist eine Norm, erfüllt also die Axiome: {\displaystyle }

Normaxiome

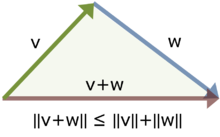
Vektoren in der Dreiecksungleichung

Jede Skalarproduktnorm erfüllt die drei Normaxiome Definitheit, absolute Homogenität und Subadditivität. Die Definitheit folgt für $v\in V$ aus der Eindeutigkeit der Nullstelle der Wurzelfunktion über

$\| v \| = 0 \; \Leftrightarrow \; \sqrt{ \langle v, v \rangle } = 0 \; \Rightarrow \; \langle v, v \rangle = 0 \; \Leftrightarrow \; v = 0$ ,

die absolute Homogenität folgt für $v\in V$ und $\alpha \in \mathbb {K}$ aus

$\| \alpha v \|^2 = \langle \alpha v, \alpha v \rangle = \bar{\alpha} \alpha \langle v, v \rangle = | \alpha |^2 \| v \|^2$

und die Subadditivität (oder Dreiecksungleichung) folgt für $v, w \in V$ über die Cauchy-Schwarz-Ungleichung (siehe den folgenden Abschnitt) aus

$\begin{align} \| v + w \|^2 & = \langle v + w, v + w \rangle = \langle v, v \rangle + \langle v, w \rangle + \langle w, v \rangle + \langle w, w \rangle = \| v \|^2 + \langle v, w \rangle + \overline{\langle v, w \rangle} + \| w \|^2 \\ & = \| v \|^2 + 2 \operatorname{Re} \langle v, w \rangle + \| w \|^2 \leq \| v \|^2 + 2 \, \| v \| \, \| w \| + \| w \|^2 = \left( \| v \| + \| w \| \right)^2 \, ,\end{align}$

wobei $\operatorname {Re}$ den Realteil der komplexen Zahl angibt und in den beiden letzten Fällen noch die (positive) Wurzel auf beiden Seiten gezogen werden muss.

Parallelogrammgleichung

Vektoren in der Parallelogrammgleichung

→ Hauptartikel: Parallelogrammgleichung

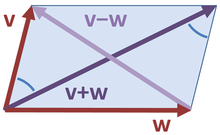
Für eine Skalarproduktnorm gilt zudem die Parallelogrammgleichung

$\| v + w \|^2 + \| v - w \|^2 = 2 ( \| v \|^2 + \| w \|^2 )$

für alle Vektoren $v, w \in V$ . Umgekehrt gilt nach dem Satz von Jordan-von Neumann: erfüllt eine Norm $\|\cdot \|$ die Parallelogrammgleichung, so ist sie von einem Skalarprodukt induziert. Dieses Resultat erhält man durch eine Polarisationsformel, bei reellen Vektorräumen zum Beispiel durch

$\langle v, w \rangle = \frac{1}{4} (\| v + w \|^2 - \| v - w \|^2 )$ .

Unitäre Invarianz

Eine Skalarproduktnorm ist weiterhin invariant unter unitären Transformationen. Ist $U\colon V \rightarrow W$ ein unitärer Operator (im endlichdimensionalen Fall eine unitäre bzw. orthogonale Matrix) von in einen weiteren Skalarproduktraum mit zugehöriger Norm, dann gilt

$\| U v \| = \| v \|$ ,

was unmittelbar aus

$\| U v \|^2 = \langle U v, U v \rangle = \langle U^{\ast} U v, v \rangle = \langle v, v \rangle = \| v \|^2$

folgt, wobei $U^{\ast}$ der zu adjungierte Operator (im endlichdimensionalen Fall die adjungierte bzw. transponierte Matrix) ist. Eine Skalarproduktnorm ändert ihren Wert somit unter unitären Transformationen des Vektors nicht. Im reellen, endlichdimensionalen Fall sind solche Transformationen beispielsweise Drehungen des Vektors um den Nullpunkt.

Cauchy-Schwarz-Ungleichung

→ Hauptartikel: Cauchy-Schwarzsche Ungleichung

Eine Skalarproduktnorm erfüllt für alle Vektoren $v, w \in V$ die Cauchy-Schwarz-Ungleichung

$\left|\langle v, w \rangle\right| \leq \| v \| \, \| w \|$ ,

wobei Gleichheit genau dann gilt, wenn und linear abhängig sind. Im reellen Fall können die Betragsstriche auch weglassen werden. Aus der Cauchy-Schwarz-Ungleichung folgt dann unmittelbar

$\frac{\langle v, w \rangle}{\| v \| \, \| w \|}\leq 1$ ,

daher kann man den Winkel $\varphi$ zwischen zwei reellen Vektoren über

$\cos(\varphi) = \frac{\langle v, w \rangle}{\| v \| \, \| w \|}$

definieren. Der Winkel $\varphi$ liegt damit im Intervall $[0,\pi ]$ , also zwischen $0^\circ$ und $180^{\circ }$ . Für Winkel zwischen komplexen Vektoren gibt es eine Reihe unterschiedlicher Definitionen.

Satz des Pythagoras

→ Hauptartikel: Satz des Pythagoras

Allgemein werden zwei Vektoren $v,w\in V$ orthogonal genannt, wenn ihr Skalarprodukt $\langle v,w\rangle =0$ ist. Für orthogonale Vektoren gilt dann der Satz des Pythagoras für Skalarprodukträume

$\| v + w \|^2 = \| v \|^2 + \| w \|^2$ ,

was direkt aus dem ersten Teil der obigen Herleitung der Dreiecksungleichung folgt. Der Satz des Pythagoras kann auch auf eine endliche Summe paarweise orthogonaler Vektoren $v_1 , \ldots , v_n \in V$ erweitert werden und es gilt dann

$\|v_{1}+\dotsb +v_{n}\|^{2}=\|v_{1}\|^{2}+\dotsb +\|v_{n}\|^{2}$ .

Die entsprechende Erweiterung auf unendlich viele Summanden in einem Hilbertraum ist die Parsevalsche Gleichung.

Verallgemeinerung

Verzichtet man auf die positive Definitheit des Skalarprodukts, erhält man die folgende Verallgemeinerung. Jede positiv semidefinite hermitesche Sesquilinearform (im reellen Fall symmetrische Bilinearform) $( \cdot, \cdot ) \colon V \times V \rightarrow {\mathbb K}$ induziert für $v\in V$ durch

$p(v) = \sqrt{( v, v )}$

eine Halbnorm. Mit dieser Halbnorm ist dann (V, p) ein halbnormierter Raum, der aber im Allgemeinen kein metrischer Raum ist. Durch Restklassenbildung lässt sich aus einer Halbnorm aber eine zugehörige Norm ableiten und so erhält man wieder einen normierten Raum und damit auch einen metrischen und einen topologischen Raum.

Beispiel

Die Kovarianz ist eine Bilinearform auf dem Raum der Zufallsvariablen mit endlichen zweiten Momenten, und wird zu einem Skalarprodukt auf dem Quotientenraum der Zufallsvariablen, die sich nur durch eine Konstante unterscheiden. Die von diesem Skalarprodukt induzierte Norm ist dann schlicht die Standardabweichung einer Zufallsvariablen.

Literatur

Herbert Amann, Joachim Escher: Analysis I. Birkhäuser, Basel 2006, ISBN 3-7643-7755-0.
Albrecht Beutelspacher: Lineare Algebra. 6. Auflage. Vieweg, 2003, ISBN 3-528-56508-X.
Bronstein et al.: Taschenbuch der Mathematik. 7. Auflage. Harri Deutsch, 2008, ISBN 978-3-8171-2007-9.
Harro Heuser: Funktionalanalysis: Theorie und Anwendung. Vieweg, 2006, ISBN 978-3-8351-0026-8.

Basierend auf einem Artikel in:

Wikipedia.de