
Inellipse
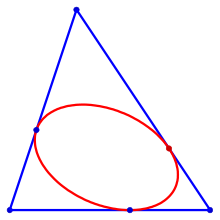
Eine Inellipse ist in der Geometrie eine Ellipse, die die Seiten eines gegebenen Dreiecks berührt. Das einfachste Beispiel ist der Inkreis. Weitere wichtige Beispiele sind die Steiner-Inellipse, die die Dreiecksseiten in deren Mitte berührt, die Mandart-Inellipse und die Brocard-Inellipse. Sie spielen in der Dreiecksgeometrie eine Rolle. Schränkt man die Ellipse nicht durch spezielle Anforderungen ein, so gibt es zu einem Dreieck unendlich viele Inellipsen.
Da ein nicht ausgearteter Kegelschnitt durch 5 Bestimmungsstücke (Punkte, Tangenten) eindeutig bestimmt ist, darf man für eine Inellipse eines Dreiecks nur auf zwei Seiten auch die Berührpunkte vorgeben. Der Berührpunkt auf der 3. Seite ist dann dadurch schon eindeutig bestimmt.
Parameterdarstellungen, Mittelpunkt, konjugierte Halbmesser

Die Inellipse des Dreiecks mit den Eckpunkten
und den zwei Berührpunkten
auf der Seite
bzw.
lässt sich durch die rationale Parameterdarstellung
beschreiben. Dabei sind
durch die Vorgaben der Berührpunkte wie folgt bestimmt:
Der 3. Berührpunkt ist
Der Mittelpunkt der Inellipse ist
Die Vektoren
sind zwei konjugierte Halbmesser und die Inellipse besitzt damit die weitere (übliche) Parameterdarstellung

Der Brianchon-Punkt
der Inellipse (gemeinsamer Punkt
der Geraden
)
ist
Mit Hilfe der Zahlen
lassen sich die zwei Berührpunkte
leicht variieren. Die Schranken für
sichern, dass die Berührpunkte wirklich auf den beiden Dreieckseiten liegen. Sie
liefern für
die Schranken
.
Man beachte, dass hier
nicht die Halbachsen der Ellipse oder Seiten des Dreiecks sind, sondern
Parameter, die die Beziehung zwischen den Berührpunkten
und den Eckpunkten
festlegen !
Beispiele

Steiner-Inellipse
Für
sind die Berührpunkte
die Seitenmitten und die Inellipse ist die Steiner-Inellipse (Mittelpunkt
ist der Schwerpunkt).
Inkreis
Für
ergibt sich der Inkreis des Dreiecks mit dem Mittelpunkt
Mandart-Inellipse
Für
erhält man die Mandart-Inellipse des Dreiecks. Sie berührt die Seiten in
den Berührpunkten der Ankreise.
Ihr Mittelpunkt ist der Mittenpunkt
des Dreiecks.

Brocard-Inellipse
Für
erhält man die Brocard-Inellipse. Sie ist durch die Vorgabe ihres
Brianchon-Punktes in trilinearen
Koordinaten
eindeutig bestimmt.
Herleitungen
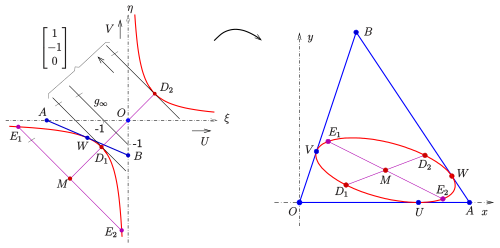
Sich entsprechende Punkte wurden in beiden Darstellungen mit denselben Buchstaben bezeichnet.
- Neue Koordinaten
Zum Beweis betrachtet man die Aufgabe projektiv und führt geeignete neue
inhomogene -
-Koordinaten
so ein, dass der gesuchte Kegelschnitt zur Hyperbel mit den Koordinatenachsen
als Asymptoten wird und
zu den Fernpunkten der Koordinatenachsen werden. Die Dreieckspunkte
werden in den neuen Koordinaten (mit eckigen Klammern) durch
beschrieben und die Gerade dazu hat die Gleichung
.
(Dass die hier verwendeten
tatsächlich mit denen in der Aussage des Satzes identisch sind, zeigt die
Rückabbildung unten.) Gesucht ist nun eine Hyperbel mit den Koordinatenachsen
als Asymptoten, die die Gerade
berührt. Man rechnet leicht nach, dass dies für die Hyperbel mit der Gleichung
der Fall ist. Sie berührt die Gerade
im Punkt
.
- Koordinatentransformation
Die Rückabbildung der gefundenen Lösung wird in homogener Darstellung durch die Matrix
beschrieben.
Ein Punkt
wird dabei auf
abgebildet, falls
ist. Ein Punkt
der
-
-Ebene wird dabei durch den Spaltenvektor
repräsentiert (siehe homogene Koordinaten). Ein Fernpunkt hat die Darstellung
.
- Koordinatentransformation wesentlicher Punkte
- (Man beachte, dass :
ist.)
ist Gleichung der Ferngerade der x-y-Ebene, Ihr Fernpunkt ist
.
Der Fernpunkt von
in der
-
-Ebene
geht also in einen Fernpunkt der x-y-Ebene über, den Fernpunkt der Gerade
.
Dies bedeutet: Die zwei in
-
-Koordinaten
zu
parallelen Tangenten der Hyperbel sind auch in den x-y-Koordinaten parallel. Die
Berührpunkte dieser Tangenten sind:
Da in der x-y-Ebene die Ellipsentangenten in den Punkten
parallel sind, ist
ein Durchmesser der Ellipse, d.h. der Mittelpunkt der Strecke
ist der Mittelpunkt
der Ellipse:
Man prüft leicht nach, dass
die
-
-Darstellung
hat. Um den zu
konjugierten Ellipsendurchmesser zu finden, muss man in der
-
-Ebene
die Schnittpunkte
der zu den Tangenten parallele Gerade durch
(sie hat die Gleichung
)
mit der Hyperbel bestimmen. Es ergibt sich
.
Und in x-y-Koordinaten
Aus den beiden konjugierten Durchmessern
lassen sich zwei vektorielle konjugierte Halbmesser
ermitteln:
Damit ergibt sich eine trigonometrische Parameterdarstellung der Inellipse:
Hieraus lassen sich, wie bei der Steiner-Ellipse, die Halbachsen, Exzentrizität, der Flächeninhalt, die Scheitel und eine Gleichung in x-y-Koordinaten der Inellipse berechnen.
Für den Berührpunkt
der Seite
gilt:
Der Brianchon-Punkt der Inellipse ist der gemeinsame Punkt
der drei Geraden
.
Man berechnet zunächst
in der
-
-Ebene
als Schnitt der drei Geraden:
und transformiert den Schnittpunkt in die x-y-Ebene. Es ergibt sich
Die punktweise Transformation der Hyperbel
liefert eine rationale Parameterdarstellung der Inellipse:
- Inkreis

Für den Inkreis gilt
und damit
- (1)
Ferner gilt in diesem Fall
- (2)
. (s. Bild)
Löst man beide Gleichungen nach
auf, erhält man
- (3)
Um den Mittelpunkt zu bestimmen, berechnet man zunächst mit Hilfe von (1) und (3)
Also ist
- Mandart-Inellipse
Die Parameter
für die Mandart-Inellipse ergeben sich aus den Angaben für die Abstände der
Berührpunkte der Ankreise (s. Ankreis)
von den Ecken.
- Brocard-Inellipse
Die Brocard-Inellipse wird durch die Vorgabe ihres Brianchon-Punktes
festgelegt. Er hat in trilinearen
Koordinaten die einfache Darstellung
.
Rechnet man die trilinearen Koordinaten in die hier geeignete Darstellung
um, so erhält man
.
Sind andererseits die Parameter
einer Inellipse vorgegeben, so ergibt sich aus der obigen Formel für
,
dass
ist. Setzt man die Ausdrücke für
jeweils gleich und löst nach
auf, so ergibt sich
Inellipse mit maximalem Flächeninhalt
- Die Steiner-Inellipse hat den größten Flächeninhalt von allen Inellipsen eines Dreiecks.
- Nachweis
Aus einem Satz
von Apollonios folgt, dass der Flächeninhalt einer Ellipse mit den
konjugierten Halbmessern
gleich
ist (s. Artikel Steiner-Ellipse).
Für die Inellipse mit den Parametern
ist (s.o.)
(Es ist .
Man beachte die Regeln für Determinanten !)
Um die Wurzeln bei der
Berechnung zu vermeiden, genügt es, die Extremstellen der Funktion
zu bestimmen:
Wegen
ergibt sich durch Vertauschen von s und t:
Auflösen der beiden Gleichungen nach s und t liefert
d.h.:
Die Steiner-Inellipse ist die Inellipse mit maximalem Flächeninhalt.
Inellipse und baryzentrische Koordinaten
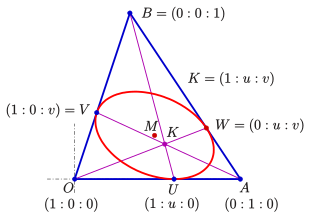
Führt man für eine baryzentrische Beschreibung mit
Parameter
so ein, dass
ist,
so gilt zwischen den obigen Parametern
und
und umgekehrt
Der 3. Berührpunkt ist dann :
und der Brianchonpunkt
hat die einfache Darstellung
Hieran erkennt man, dass die Inellipse auch durch die Lage ihres Brianchonpunktes (und des Dreiecks) eindeutig beschrieben wird.
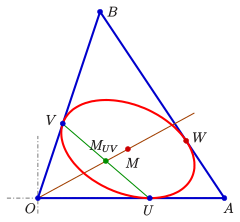
Der Mittelpunkt der Ellipse ist
Dieses Ergebnis kann man aus der obigen Formel für den Mittelpunkt ableiten oder die Eigenschaft
- Der Mittelpunkt
der Sehne
liegt auf der Gerade
verwenden. (Die Richtungen der Geraden
sind bezüglich der Ellipse konjugiert.)
Diese Eigenschaft gilt entsprechend auch für
und
.
kann also in baryzentrischen Koordinaten als Schnittpunkt der Geraden
berechnet
werden. Aber auch die zeichnerische Bestimmung von
ist damit möglich.
Der Vorteil der baryzentrischen Beschreibung besteht in ihrer Übersichtlichkeit. Die x-y-Koordinaten von Punkten lassen sich leicht aus ihren baryzentrischen Koordinaten mit der Schwerpunkt-Formel berechnen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.01. 2022