Komplementärraum

Ein komplementärer Unterraum, kurz Komplementärraum oder Komplement, ist im mathematischen Teilgebiet der linearen Algebra ein möglichst großer Unterraum eines Vektorraums, der einen vorgegebenen Unterraum nur im Nullpunkt schneidet. Der gesamte Vektorraum wird dadurch gewissermaßen in zwei unabhängige Teile zerlegt.

Komplement eines Untervektorraums

Definition

Es sei ein Vektorraum über einem Körper und ein Untervektorraum von . Dann heißt ein Untervektorraum komplementär oder ein Komplement zu , wenn die Bedingungen

$U\cap W=\{0\}$

und

erfüllt sind. Dabei ist $\{0\}$ der Nullvektorraum und U+W steht kurz für

$\{u+w\mid u\in U,w\in W\}.$

Bemerkungen und Eigenschaften

Man sagt dann auch: ist die innere direkte Summe von und und schreibt $V=U\oplus W$ .
Sind Unterräume von und $U\oplus W$ ihre äußere direkte Summe, dann gilt: Der Homomorphismus

$U\oplus W\to V,\ \ (u,w)\mapsto u+w$

ist genau dann ein Isomorphismus, wenn und komplementär sind, d.h. wenn die innere direkte Summe von und ist.

Zu einem Untervektorraum eines Vektorraumes existiert stets ein komplementärer Untervektorraum. Das folgt aus dem Basisergänzungssatz. Komplemente sind aber im Allgemeinen nicht eindeutig bestimmt.
ist genau dann ein Komplement von in , wenn sich jeder Vektor $v\in V$ eindeutig als

mit $u\in U$ und $w\in W$ schreiben lässt.

Für die Dimensionen der entsprechenden Untervektorräume gilt

$\dim V=\dim U+\dim W.$

Die Dimension des Komplementärraums wird auch als Kodimension von in bezeichnet.

Ist ein Komplement zu , so ist auch ein Komplement zu .
Die Einschränkung der kanonischen Projektion $V\to V/U$ auf ist ein Isomorphismus, siehe Faktorraum.

Zusammenhang mit Projektionen

Es sei ein Unterraum im Vektorraum .

Ist ein Komplementärraum von , so kann man nach obigem jedes Element aus eindeutig als Summe mit $u\in U$ und $w\in W$ darstellen. Dann ist $P_{W}\colon V\rightarrow V,v=u+w\mapsto u$ eine Projektion mit dem Bild $\operatorname {im}P_{W}=U$ und Kern $\operatorname {ker}P_{W}=W$ .

Ist umgekehrt $P\colon V\rightarrow V$ eine Projektion mit Bild , so ist der Kern $\operatorname {ker}P$ ein Komplementärraum von .

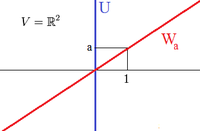
Man erhält auf diese Weise eine Bijektion von der Menge aller Komplementärräume von auf die Menge aller Projektionen auf mit Bild . Die Projektionen mit Bild bilden einen affinen Raum über dem Vektorraum $\operatorname {Hom}(V/U,U)\subset \operatorname {Hom}(V,V)$ .

Jeder Unterraum $W_{a}$ ist ein Komplement zu .

Beispiel

Wir betrachten den Unterraum $U:=\{(0,y);\,y\in \mathbb{R} \}\subset V=\mathbb{R} ^{2}$ wie in nebenstehender Zeichnung. Zu jeder reellen Zahl sei $W_{a}$ die Gerade durch 0 mit Steigung . Jeder solche Unterraum $W_{a}$ ist ein zu komplementärer Unterraum von . Die zugehörige Projektion hat die Matrixdarstellung $P_{a}={\begin{pmatrix}0&0\\-a&1\end{pmatrix}}$ . Man sieht der Matrixdarstellung direkt an, dass das Bild ist, denn die erste Zeile der Matrix besteht nur aus Nullen. Der Kern von P_a ist $W_{a}$ , denn aus $P_{a}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}$ folgt ${\begin{pmatrix}0\\0\end{pmatrix}}={\begin{pmatrix}0&0\\-a&1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}0\\-ax+y\end{pmatrix}}$ , das heißt, der Kern besteht aus allen Punkten ${\begin{pmatrix}x\\y\end{pmatrix}}$ mit y=ax , und das ist genau die Gerade durch 0 mit Steigung .

Orthogonales Komplement

Definition

Es sei ein Vektorraum über einem Körper , auf dem eine symmetrische oder alternierende Bilinearform oder eine hermitesche Sesquilinearform $\langle \cdot ,\cdot \rangle$ gegeben ist. Für einen Unterraum $U\subseteq V$ heißt

$U^{\perp }:=\{v\in V\mid \forall u\in U:\langle u,v\rangle =0\}$

das orthogonale Komplement oder der Orthogonalraum von in . Man beachte, dass es im Allgemeinen kein Komplement von im oben definierten Sinne ist. Der Dualitätssatz besagt jedoch, dass, falls endlichdimensional und $\langle \cdot ,\cdot \rangle$ sowohl auf als auch auf dem Unterraum nicht ausgeartet ist, $V=U\oplus U^{\bot }$ gilt.

Die letzte Eigenschaft ist beispielsweise für Skalarprodukte auf reellen oder komplexen Vektorräumen stets erfüllt.

Orthogonales Komplement in Hilberträumen

Ist ein Hilbertraum, so ist das orthogonale Komplement eines Unterraumes ein Komplement seines Abschlusses ${\bar U}$ , d.h.

$V={\bar U}\oplus U^{\perp }$ , wobei $\oplus$ als innere orthogonale Summe gelesen werden kann.

Das orthogonale Komplement ist stets abgeschlossen, und es gilt

$(U^{\perp })^{\perp }={\bar U}$ .

Komplemente in Banachräumen

Sei ein (endlichdimensionaler oder unendlichdimensionaler) vollständiger, normierter Vektorraum, also ein Banachraum und sei ein abgeschlossener Unterraum zu dem ein abgeschlossener Komplementärraum existiert, so dass die Räume und $U\oplus W$ algebraisch isomorph sind, dann ist der durch $U\oplus W\rightarrow V,\,(u,w)\mapsto u+w$ definierte Isomorphismus auch ein topologischer Isomorphismus. Das heißt die Abbildung und ihre Umkehrabbildung sind stetig.

In Banachräumen haben abgeschlossene Unterräume nach obigem stets einen Komplementärraum, aber das bedeutet nicht, dass man auch einen abgeschlossenen Komplementärraum finden könnte. Dies ist vielmehr eine Charakterisierung der topologischen Vektorraumstruktur von Hilberträumen, in denen man stets das orthogonale Komplement zur Verfügung hat, denn es gilt folgender Satz von Joram Lindenstrauss und Lior Tzafriri:

Ein Banachraum ist genau dann stetig isomorph zu einem Hilbertraum, wenn jeder abgeschlossene Unterraum einen abgeschlossenen Komplementärraum besitzt.

Zur Existenz von Komplementärräumen gilt folgender Satz von Kazimierz Sobczyk:

Ein zum Folgenraum c₀ isomorpher Unterraum eines separablen Banachraums hat stets einen abgeschlossenen Komplementärraum.

Im nicht-notwendigerweise-separablen Fall gilt die Aussage dagegen nicht: Man kann zeigen, dass zu $c_{0}\subset \ell ^{\infty }$ kein abgeschlossener Komplementärraum existiert.

Invariante Komplemente

Sei ein Vektorraum, $f \colon V \to V$ ein Endomorphismus von und ein -invarianter Unterraum, d.h. $f(U)\subseteq U$ . Dann besitzt nicht immer ein -invariantes Komplement. Gibt es zu jedem invarianten Unterraum ein invariantes Komplement, heißt der Endomorphismus halbeinfach. Über algebraisch abgeschlossenen Körpern ist Halbeinfachheit äquivalent zu Diagonalisierbarkeit.

Analoge Begriffe werden in der Darstellungstheorie verwendet. Für eine unitäre Darstellung ist das orthogonale Komplement eines invarianten Unterraums wieder invariant, folglich ist jede endlichdimensionale unitäre Darstellung halbeinfach.

Wenn man die invarianten Unterräume als Untermoduln interpretiert, werden die invarianten Komplemente zu komplementären Untermoduln im Sinn des folgenden Abschnitts.

Verallgemeinerung

Die Definition von Komplementen lässt sich wörtlich auf Moduln verallgemeinern. Allerdings gibt es zu einem Untermodul eines Moduls über einem Ring nicht mehr stets einen komplementären Untermodul. Ein Modul, in dem jeder Untermodul ein Komplement besitzt, wird halbeinfacher Modul genannt. In dieser Sprechweise sind also beispielsweise Vektorräume halbeinfache Moduln. Der $\mathbb {Z}$ -Modul $\mathbb {Z}$ ist nicht halbeinfach, weil der Untermodul $2\mathbb {Z}$ kein Komplement besitzt.

Statt „besitzt ein Komplement“ sagt man auch „ist ein direkter Summand“. Projektive Moduln sind dadurch charakterisiert, dass sie isomorph zu direkten Summanden freier Moduln sind. Injektive Moduln sind dadurch charakterisiert, dass sie in jedem Obermodul ein Komplement besitzen.

Die Beziehung zu Projektionen sowie die einfach transitive Operation von $\operatorname {Hom}(V/U,U)$ auf der Menge der Komplemente von in überträgt sich ebenfalls auf den Modulfall (sogar auf beliebige abelsche Kategorien).

Basierend auf einem Artikel in:

Wikipedia.de