Kettenbruch
In der Mathematik und insbesondere der Zahlentheorie ist ein Kettenbruch (fortgesetzter Bruch) ein Ausdruck der Form
Ein Kettenbruch ist also ein gemischter
Bruch der Form ,
bei dem der Nenner
wieder die Form eines gemischten Bruchs besitzt, wobei sich dieser Aufbau weiter
so fortsetzt.
Jede reelle Zahl kann als ein
Kettenbruch mit ganzen Zahlen
ausgedrückt werden. Kettenbrüche können daher als Zahlensystem
bezeichnet werden, wie das Dezimalsystem.
Sie dienen jedoch in erster Linie nicht zum Rechnen, sondern werden dazu
verwendet, Approximationsaufgaben
zu lösen: So liefern sie in der Zahlentheorie Näherungen für reelle Zahlen,
indem diese durch einen Bruch aus ganzen Zahlen ausgedrückt werden, und in der
numerischen
Mathematik approximiert man durch sie Funktionen, ähnlich wie dies auch
mittels Potenzreihen erreicht wird.
Von besonderer Bedeutung sind reguläre Kettenbrüche. Bei dieser Form
haben alle Zähler
den Wert
.
Ein regulärer Kettenbruch ist also durch die Folge
bestimmt, und man schreibt ihn platzsparend als
.
Kettenbrüche spielen zudem eine große Rolle in der Zahlentheorie. So zeigte zum Beispiel Joseph Liouville 1844 mit ihrer Hilfe, dass transzendente Zahlen existieren. Außer in der Zahlentheorie kommen Kettenbrüche in der Kryptographie, algebraischen Geometrie, Topologie, Funktionentheorie, numerischen Mathematik und bei der Analyse chaotischer Systeme zur Anwendung.

Geschichte
| Regulärer Kettenbruch [1] |
| Johann Heinrich Lambert
Kettenbruch für |
| Lamberts Kettenbruch für den Tangens |
Kettenbrüche werden seit dem 16. Jahrhundert dazu verwendet, „gute
Näherungsbrüche“ für irrationale
Zahlen zu finden. Das bekannteste Beispiel ist die Näherung
für
.

Rafael Bombelli verwendete Kettenbrüche bereits 1579, um damit Quadratwurzeln zu berechnen. Im Jahr 1613 veröffentlichte Pietro Cataldi ein Buch, in dem unter anderem auch Kettenbrüche auftauchen. 1636 finden sich Kettenbrüche im Buch „Deliciae Physico-Mathematicae“ von Daniel Schwenter und ab 1655 in mehreren Büchern von John Wallis. Aus dem Bedürfnis, Brüche mit großen Nennern sowie natürliche Konstanten zu approximieren, beschäftigte sich zunächst Christiaan Huygens im 17. Jahrhundert mit Kettenbrüchen. Er berechnete damit aus den Umlaufzeiten der Planeten das Übersetzungsverhältnis der Zahnräder für sein Zahnradmodell des Sonnensystems. Huygens ermittelte für die Umlaufzeit um die Sonne das Verhältnis zwischen Saturn und Erde als
Der reguläre Kettenbruch hierfür beginnt mit .
Approximiert man dieses Verhältnis mit dem Näherungsbruch, der entsteht, wenn
man nur die ersten vier Einträge verwendet, dann beträgt der Fehler [2] nur
,
da
In Leonhard Eulers Korrespondenz [3] treten Kettenbrüche hingegen zuerst in einem ganz anderen Zusammenhang auf, nämlich in Verbindung mit der Riccatischen Differentialgleichung. Bald jedoch interessierte sich Euler für Kettenbrüche um ihrer selbst willen. Er entdeckte nämlich die folgenden drei wichtigen Eigenschaften:
- Jede rationale Zahl kann durch einen endlichen regulären Kettenbruch dargestellt werden (der mit Hilfe des euklidischen Algorithmus berechnet werden kann).
- Periodische reguläre Kettenbrüche stellen quadratische Irrationalzahlen dar; diese Aussage bewies Euler als Erster.
- Die Entwicklung jeder reellen Zahl in einen regulären Kettenbruch liefert die besten rationalen Approximationen für diese Zahl.
Einige dieser Erkenntnisse hatte bereits Huygens gewonnen, dessen Arbeit Euler aber unbekannt war. Eulers Arbeiten – und darauf aufbauend die von Joseph-Louis Lagrange – begründeten die Theorie der Kettenbrüche.
Zur rationalen Approximation existiert neben dem Algorithmus
von Euler auch ein Algorithmus von Lord William Brouncker. Euler zeigte um 1759, dass die beiden Algorithmen identisch sind.
Johann Heinrich Lambert benutzte Kettenbrüche in seiner Arbeit von 1766 dazu, die
Irrationalität von
zu zeigen. Seine Kettenbruchentwicklung der Tangensfunktion ist in der Abbildung
rechts dargestellt.
Moritz Abraham Stern schuf 1832 die erste systematische Zusammenfassung der Theorie der Kettenbrüche. Im 19. Jahrhundert entwickelte sich die Theorie rasch weiter und so veröffentlichte Oskar Perron im Jahre 1913 eine Zusammenfassung des Wissensstandes, die bis heute als ein Standardwerk gilt (Neuauflage 1954/57).
Weitere wichtige Anwendungen waren und sind: Beweise für die Irrationalität oder die Transzendenz spezieller Zahlen und die Ermittlung von Schaltjahren (da ein Jahr mit 365,24219 Tagen etwas kürzer als 365¼ Tage ist, bedarf es zusätzlich zum Schalttag alle vier Jahre einer weiteren Korrektur; die beste Wahl dafür lässt sich mit Kettenbrüchen begründen).
Definition
Begriff des Kettenbruchs
Ein (unendlicher) Kettenbruch ist ein fortgesetzter Bruch der Form
oder (regulärer Fall)
mit
und
für
.
Die Brüche
bzw.
werden Teilbrüche genannt,
heißt der
-te
Teilzähler und
der
-te
Teilnenner. [4]
Ein Kettenbruch, der sich nach einem Teilbruch
nicht weiter fortsetzt, ist ein endlicher Kettenbruch.
Eine formalere Definition findet man im Abschnitt Darstellung als Komposition von Abbildungen.
Reguläre Kettenbrüche sind in der Zahlentheorie der bei weitem wichtigste
Kettenbruch-Typ. Bei der Approximation von (reellen oder komplexen)
Funktionen verwendet man auch Kettenbrüche mit Unbekannten, siehe zum
Beispiel den Lambertschen Kettenbruch für die Tangensfunktion im Abschnitt
„Geschichte“. Manchmal benötigt man einen endlichen regulären Kettenbruch, bei
dem der letzte Eintrag
eine reelle (nicht-ganze) Zahl ist. Dies ermöglicht zum Beispiel die
Schreibweise
usw. für die goldene
Zahl. Auch werden bisweilen allgemeine Kettenbrüche mit
benutzt.
Notation
Die Kurzschreibweise für einen allgemeinen Kettenbruch ist
In Anlehnung an die Summen- und Produktzeichen
und
führte Gauß
hierfür auch die folgende Schreibweise ein:
Ein regulärer Kettenbruch wird oft in der folgenden Weise geschrieben:[5]
wird nur deshalb gesondert aufgeführt, weil es aus
ist, die nachfolgenden
aber immer nur aus
sind.
Die Notation für endliche Kettenbrüche ist dementsprechend
Darstellung als Komposition von Abbildungen
Man kann einen Kettenbruch auch als eine Komposition
von Abbildungen
darstellen. Dies liefert eine formalere Definition als die bisher gegebene.
Hierfür setzt man
und erhält
Die Definition unendlicher Kettenbrüche erfolgt durch eine Grenzwertbetrachtung im Abschnitt Unendliche Kettenbrüche.
Endliche Kettenbrüche
Endliche Kettenbrüche und ihre Näherungsbrüche
Von nun an betrachten wir ausschließlich reguläre Kettenbrüche. Bricht man
den Kettenbruch
nach dem
-ten
Glied ab
,
so heißt
sein -ter
Näherungsbruch (oder auch
-te
Konvergente). Die ersten Näherungsbrüche lauten offenbar
.
Bei dem Beispiel 41/29 = [1;2,2,2,2] sind das die Brüche .
Der dritte Näherungsbruch lautet
und der vierte ist gleich
,
also identisch zum Ausgangsbruch.
Mit vollständiger
Induktion beweist man das Bildungsgesetz für die Näherungsbrüche (
und
werden pro forma auch für
definiert, damit die Formeln ab
stimmen):
sowie die Beziehung
.
Daraus folgt, dass Näherungsbrüche stets in gekürzter Form vorliegen (wenn
und
beide durch eine natürliche Zahl größer als
teilbar wären, dann müsste auch die rechte Seite durch diese Zahl teilbar sein,
was aber nicht der Fall ist). Dividiert man durch
,
so folgt:
|
|
|
(1) |
|
|
Beispielsweise hat man für den zweiten und dritten Näherungsbruch von
die Beziehung
.
Auf ähnliche Weise zeigt man
und
|
|
|
(2) |
|
|
Diese Formeln sind grundlegend für die weiter unten besprochenen Konvergenzfragen bei unendlichen Kettenbrüchen.
Matrixdarstellung
Das Bildungsgesetz für die Näherungsbrüche lässt sich auch elegant in Matrixform schreiben. Man erhält dann (wieder mit vollständiger Induktion zu beweisen):
Da die Determinante
jeder der Matrizen auf der linken Seite
beträgt, folgt sofort:
und Multiplikation mit
zeigt erneut die oben angegebene Gleichung.
Durch Transposition
der Matrizen folgt nun (da die Transposition die Reihenfolge der Matrizen
umkehrt), dass
sowie
gelten.
Beispiel: Die Näherungsbrüche von
lauten
,
,
und
.
Es gilt
und man bekommt
sowie
.
Endliche Kettenbrüche und der euklidische Algorithmus
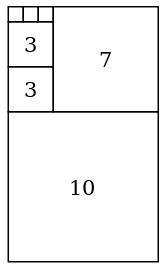
Die Umwandlung einer rationalen Zahl in einen Kettenbruch erfolgt mit Hilfe des euklidischen Algorithmus.
Als Beispiel rechnen wir für
wie folgt:
Siehe dazu auch den Abschnitt Kettenbruchzerlegung im Artikel über den euklidischen Algorithmus. In der Abbildung ist dieses Verfahren veranschaulicht. Aus der folgenden Gleichungskette ist ersichtlich, dass die Kettenbruchentwicklung durch wiederholtes Einsetzen der Gleichungen des euklidischen Algorithmus entsteht:
Das graphische Verfahren kann so erläutert werden: Man beginnt mit einem
großen Rechteck. Darin bringt man so viele Quadrate der Seitenlänge
unter, wie möglich (in diesem Beispiel geht das nur einmal). Es bleibt nun ein
großes Rechteck unbedeckt, auf das man die Überlegung weiter anwendet. Die
Anzahl der jeweils verwendeten Quadrate sind dabei die Teilnenner des
Kettenbruchs.
Unendliche Kettenbrüche
Unendliche Kettenbrüche: Konvergenz und Näherungsbrüche
Für eine (unendliche) Folge
ist der Kettenbruch
nur dann definiert, wenn die Folge der Näherungsbrüche
konvergiert.
In diesem Fall hat der unendliche Kettenbruch
den Wert
.
Da hier nur reguläre Kettenbrüche behandelt werden, gilt: Jeder unendliche Kettenbruch konvergiert.[6]
Das erkennt man folgendermaßen: Die Folge der Näherungsbrüche mit geraden
Indizes, also
ist aufgrund Gleichung (2) monoton
steigend, während die Folge mit ungeraden Indizes
monoton fallend ist, siehe Abbildung. Da außerdem jeder ungerade Näherungsbruch
größer ist als jeder gerade, sind beide Folgen monoton und beschränkt und
konvergieren daher. Ihre beiden Grenzwerte sind aber aufgrund Gleichung (1)
gleich (da die
beliebig groß werden, geht die Differenz gegen 0).
Nun betrachte man
Aus den oben angegebenen Formeln lässt sich die Differenz zwischen
und dem
-ten
Näherungsbruch abschätzen:
|
|
|
(3) |
|
|
Als Beispiel für Gleichung (3) betrachte man den Kettenbruch der
Quadratwurzel von 2. Im Abschnitt Periodische Kettenbrüche wird gezeigt,
dass .
Die ersten Näherungsbrüche dieses unendlichen Kettenbruchs sind ,
,
,
,
und Gleichung (3) besagt in diesem Fall für
:
.
Klar ist nun, dass jede rationale Zahl einen endlichen Kettenbruch hat und
dass jeder endliche Kettenbruch eine rationale Zahl darstellt. Diese Darstellung
ist nicht eindeutig, da man das Ende des Kettenbruchs auf zwei Arten schreiben
kann, ohne den Wert zu verändern: Man kann zwischen den Darstellungen
und
wechseln. Jede irrationale Zahl hat aber eine eindeutige Darstellung:
Satz (Rationale und irrationale Zahlen, Eindeutigkeit der Darstellung):
Jede reelle Zahl kann als (regulärer) Kettenbruch dargestellt werden. Für irrationale Zahlen ist die Kettenbruchdarstellung unendlich und eindeutig. Rationale Zahlen entsprechen endlichen Kettenbrüchen und jede rationale Zahl hat genau zwei Kettenbruchdarstellungen.
Für den Beweis der Aussage, dass jeder unendliche Kettenbruch eine
irrationale Zahl darstellt, gilt: Betrachtet man
und nimmt an, dass
rational wäre, so ist
und Multiplikation mit
und
ergibt
.
Da die
für wachsendes
beliebig groß werden und die Zahl zwischen den Betragsstrichen stets eine ganze
Zahl ist, liefert das einen Widerspruch. Somit ist
nicht rational.
Unendliche Kettenbrüche und der verallgemeinerte euklidische Algorithmus
Für irrationale Zahlen
wird eine Verallgemeinerung des euklidischen Algorithmus verwendet. Dieser
funktioniert auch für rationale Zahlen; wir prüfen deshalb in jedem Schritt, ob
der Algorithmus abbricht:
- Ist
keine ganze Zahl, so setzt man
(Ganzteil von
) und
auf das Inverse des Rests, also
.
- Falls
nicht ganz ist, dann setzt man
und
.
Dieses Verfahren wird fortgesetzt, bis man ein ganzzahliges
erhält (das geschieht natürlich nur dann, wenn der Startwert rational ist). Bei
einem irrationalen
bricht das Verfahren nicht ab. Die Zahlen
werden vollständige Quotienten genannt. Es gilt
.
Ähnlich wie das Bildungsgesetz für die Näherungsbrüche beweist man:
|
|
|
(4) |
|
|
Beispiele: Wir berechnen die Kettenbruchentwicklung von
bis zur zweiten Stelle:
also
,
also
,
also
.
Sie lautet also .
Weitere Stellen gibt es im Artikel Kreiszahl,
ein Muster wurde jedoch bislang in der regulären Kettenbruchentwicklung von
nicht entdeckt.
Im Gegensatz dazu findet man ein klares Muster im Kettenbruch der eulerschen Zahl :
.
Bei der dritten Wurzel von
gibt es wiederum kein Muster:
Als Beispiel für die Verwendung von Gleichung (4) betrachte man die
aufeinanderfolgenden Näherungsbrüche 17/12 und 41/29 von .
Da die vollständigen Quotienten für
gleich
sind, gilt:
Wie im Abschnitt „Geschichte“ erwähnt, fand Euler heraus, dass
periodische Kettenbrüche (so wie bei der Quadratwurzel von
oder bei der goldenen Zahl) quadratischen Irrationalzahlen entsprechen, und
Lagrange zeigte später, dass alle diese Zahlen periodische Kettenbrüche haben.
Diesem Thema ist der übernächste Abschnitt gewidmet.
Äquivalente Zahlen
Zwei reelle Zahlen
heißen äquivalent,
wenn es ganze Zahlen
mit
gibt, sodass
gilt. Das heißt, sie sind durch eine ganzzahlige Möbiustransformation
mit Determinante
verbunden (Elementen der speziellen linearen Gruppe
).
Man sieht leicht, dass diese Definition tatsächlich eine Äquivalenzrelation
auf den reellen Zahlen liefert: Mit
ist die Reflexivität gezeigt, mit
folgt die Symmetrie, und die Transitivität kann man explizit nachrechnen.
Jede rationale Zahl ist äquivalent zu 0, alle rationalen Zahlen bilden also eine Äquivalenzklasse. Daher ist diese Einteilung der reellen Zahlen hauptsächlich für irrationale Zahlen interessant. Die Beziehung zu ihren regelmäßigen Kettenbruchentwicklungen ergibt sich durch folgenden Satz von Serret:
Satz: Zwei irrationale Zahlen
sind genau dann äquivalent, wenn ihre Kettenbruchdarstellungen
und
so beschaffen sind, dass es natürliche Zahlen
und
gibt, sodass für alle
gilt.
Die Übereinstimmung in ihren Kettenbruchdarstellungen bis auf eine unterschiedliche Anfangssequenz führt bei äquivalenten Zahlen zu asymptotisch gleichen Approximationseigenschaften. Ein Beispiel ist im Abschnitt Sätze über quadratische Approximierbarkeit angeführt (Gleichung 5).
Periodische Kettenbrüche

Bei der Dezimaldarstellung
reeller Zahlen entsprechen periodische Darstellungen den rationalen Zahlen. Man
unterscheidet rein-periodische Dezimalbrüche, z.B. ,
und solche mit einer Vorperiode, wie bei
.
Bei Kettenbrüchen spielen periodische Darstellungen ebenfalls eine besondere Rolle. Wie Euler und Lagrange herausfanden, entsprechen sie den quadratischen Irrationalzahlen (irrationale Lösungen quadratischer Gleichungen mit rationalen Koeffizienten). Insbesondere sind die Kettenbrüche derjenigen reellen Zahlen, die weder rational noch quadratische Irrationalzahlen sind, nicht-periodisch.
Ein Kettenbruch wird periodisch genannt, wenn es Zahlen
gibt, so dass für die Teilnenner
für alle
gilt. Das minimale
mit dieser Eigenschaft nennt man die Periode des Kettenbruchs, der dann in der
Form
geschrieben wird. Ist auch
minimal gewählt, heißt die Folge
die Vorperiode und
ihre Länge.
Satz von Euler-Lagrange
Satz: Jeder periodische Kettenbruch ist eine quadratische Irrationalzahl und umgekehrt.
Der erste Teil des Satzes ist einfacher zu beweisen und stammt von Euler, während die Umkehrung schwieriger ist und erst später von Lagrange bewiesen wurde.
Beispiele
- Sei
. Dann gilt
, also ist
Wurzel der quadratischen Gleichung
, woraus
folgt (da die andere Nullstelle negativ ist). Daher ist
die goldene Zahl (siehe auch den Artikel Goldener Schnitt).
- Sei
. Wir betrachten
. Dann ist
, woraus
und
folgt. Da
gilt, muss
sein. Daher gilt
.
- Sei
. Wir betrachten
. Dann ist
, also
, woraus
und
folgt. Da
gilt, muss
sein. Daher gilt
.
- Eine besondere Form periodischer unendlicher Kettenbrüche haben die
sogenannten „noblen
Zahlen“: Ihre Kettenbruchentwicklung endet stets mit
. Die goldene Zahl ist das wohl prominenteste Beispiel einer noblen Zahl.
- Die Kettenbrüche irrationaler Quadratwurzeln rationaler Zahlen größer als
1 haben eine besondere Symmetrie: Für jede rationale Zahl
, die nicht Quadrat einer rationalen Zahl ist, gilt
-
-
- und umgekehrt ist das Quadrat jedes Kettenbruchs dieser Form eine rationale Zahl.
- Die Vorperiode hat also stets Länge
, der periodische Block ist symmetrisch und wird beendet mit
. Beispiele dafür sind außer den Wurzeln von
und
:
- Der Kettenbruch der Quadratwurzel von
in einem Werk von Euler über die Pellsche Gleichung ist rechts abgebildet.[7] Die goldene Zahl aus Beispiel 1 hat diese Form nicht. Ein weiteres „Gegen“-Beispiel dieser Art ist
.
-
Pellsche Gleichung
Periodische Kettenbrüche werden zur Lösung der Pellschen Gleichung
verwendet.
Beste Näherungen
Zwei Möglichkeiten bester Näherung
In der Einleitung wurde erwähnt, dass die Bestimmung von „guten Näherungsbrüchen“ eine wichtige Anwendung von Kettenbrüchen ist. Es gilt nämlich, dass jeder Näherungsbruch der Kettenbruchentwicklung einer reellen Zahl eine besonders gute rationale Näherung dieser Zahl ist.
Da man jede irrationale Zahl beliebig genau durch rationale Zahlen approximieren kann, gibt es keine absolute beste Näherung an eine irrationale Zahl. Man unterscheidet stattdessen zwei Arten von „Rekordnäherungen“:
Definition: Ein Bruch
ist eine beste Näherung 1. Art für die reelle Zahl
,
wenn für alle Brüche
mit
und
gilt:
Einen besseren Näherungsbruch kann man also nur bekommen, wenn man größere
Nenner als
erlaubt.
(Der Einfachheit halber beschränken wir uns auf positive reelle Zahlen und
betrachten daher nur natürliche Zahlen
als Zähler und Nenner.) Weiter:
Ein Bruch
ist eine beste Näherung 2. Art für die reelle Zahl
,
wenn für alle Brüche
mit
und
gilt:
Beide Begriffe bester Näherung werden – je nach Anwendung – gebraucht.
Die stärkere Bedingung ist die zweite: Angenommen, es gibt einen Bruch
mit
und
,
dann liefert die Multiplikation mit
die Ungleichung
.
Das zeigt, dass ein Bruch, der nicht beste Näherung der 1. Art ist, auch
keine beste Näherung 2. Art sein kann. Daraus folgt, dass jede beste
Näherung 2. Art ebenso eine beste Näherung 1. Art ist.
Beispiel: Wir betrachten .
Die Näherungsbrüche
,
,
lauten
,
und
und sie bilden die vollständige Liste der besten Näherungen 2. Art. Es gibt
jedoch weitere beste Näherungen 1. Art, nämlich
und
.
Dieses Thema wird in den nächsten beiden Abschnitten behandelt.
Näherungsbrüche sind beste Näherungen
Die Nützlichkeit der Näherungsbrüche zeigt sich in folgendem Satz:
Satz (Lagrange):
Für jede reelle Zahl gilt: Jeder Näherungsbruch
mit
ist eine beste Näherung 2. Art (und daher auch eine beste Näherung
1. Art).
Für einen 0-ten Näherungsbruch gilt dies nicht immer, da dieser
beispielsweise bei
den Wert
hat, aber die ganze Zahl
eine bessere Näherung mit Nenner
darstellt. [8]
Man kann diesen Satz im Fall von besten Näherungen 2. Art umkehren:
Satz: Jede beste Näherung 2. Art einer reellen Zahl ist ein Näherungsbruch ihrer (regulären) Kettenbruchentwicklung.
Für Näherungen 1. Art gilt dies jedoch nicht, wie oben im Beispiel 17/10 dargestellt. Man kann jedoch die zusätzlich auftretenden Brüche charakterisieren: Sie entstehen als Medianten (Farey-Summen) von Näherungsbrüchen und werden Nebennäherungsbrüche genannt. Näheres dazu im nächsten Abschnitt.

Beispiel: Angenommen, man sucht die kleinste natürliche Zahl ,
für die der Abstand von
von der nächstgelegenen ganzen Zahl kleiner als
ist. Aufgrund des letzten Satzes muss
in der Folge der Näherungsbruch-Nenner
von
enthalten sein. Die ersten Nenner lauten, wie schon oben ausgerechnet,
.
Sie genügen aufgrund der periodischen Teilnenner der Rekursion
(eine Lucas-Folge). Der
Näherungsbruch
ist gleich
und es gilt
,
sodass der Abstand zu
kleiner als die geforderte Genauigkeit ist. Das gesuchte
ist also gleich
,
da die Genauigkeit von
für
nicht erreicht ist.
Die gleiche Frage für die goldene Zahl
führt zur Überprüfung von
für Elemente
der Fibonacci-Folge
und man erhält als Ergebnis
.
Approximation von oben und unten, Nebennäherungsbrüche
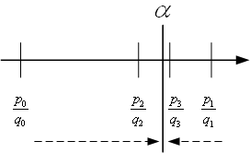
Schon 1770 hatte sich Lagrange mit dem Thema beschäftigt, welche Näherungen 1. Art zusätzlich zu den Näherungsbrüchen auftreten (siehe Abbildung rechts). Er wurde zu den „fractions secondaires“ geführt, die im Deutschen Nebennäherungsbrüche genannt werden.
Es handelt sich um Medianten benachbarter Näherungsbrüche:
Definition: Für zwei positive Brüche ,
mit
heißt
der Mediant (oder die Farey-Summe)
der beiden Brüche. Der Mediant hat die einfach zu zeigende Eigenschaft, dass
.
Aufgrund dieser Eigenschaft kann man die Bildung des Medianten wiederholt ausführen (iterieren) und bekommt Brüche der Form
die eine aufsteigende Folge bilden. Für die folgende Definition der Nebennäherungsbrüche werden also iterierte Medianten benachbarter Näherungsbrüche gebildet:
Definition: Die zu einem Kettenbruch gehörenden Brüche
heißen Nebennäherungsbrüche. Sie liegen zwischen dem -ten
und dem
-ten
Näherungsbruch. Für gerades
bilden sie eine steigende Folge und für ungerades
eine fallende Folge.
Anmerkung: im besonderen Fall
verwendet man
,
und erhält eine fallende Folge, die größer ist als
.
Satz (Lagrange 1798): Jede beste Näherung 1. Art einer reellen Zahl ist ein Näherungsbruch oder ein Nebennäherungsbruch ihrer Kettenbruchentwicklung.
Eine Charakterisierung der Menge der Näherungsbrüche und Nebennäherungsbrüche kann man wie folgt erhalten:
Satz (Lagrange 1798):
Für jede reelle Zahl
gilt:
a) Jeder Bruch, der zwischen
und einem Näherungs- oder Nebennäherungsbruch liegt, hat einen größeren Nenner
als dieser.
b) Ist umgekehrt ein Bruch
von der Art, dass jeder Bruch, der zwischen
und
liegt, einen Nenner größer als
hat, dann ist
ein Näherungs- oder Nebennäherungsbruch.
In anderen Worten: Betrachtet man nur approximierende Brüche größer als
(oder umgekehrt kleiner als
),
so sind die Rekordnäherungen vollständig durch die Menge der Näherungs- oder
Nebennäherungsbrüche beschrieben.

In der Definition der besten Näherung 1. Art werden aber die Approximationen von oben und unten gleichzeitig betrachtet. Die Analyse dieser Situation (Verfeinerung des vorletzten Satzes) ergibt:
Satz:
Es sei
die Anzahl der Nebennäherungsbrüche zwischen dem
-ten
und dem
-ten
Näherungsbruch. Dann gilt: Ist
gerade, so ergibt die zweite Hälfte der Nebennäherungsbrüche beste Näherungen
1. Art, die erste Hälfte aber nicht. Das Gleiche gilt – mit Ausnahme
des mittleren Elements –, wenn
ungerade ist. Für den mittleren Bruch gibt es eine kompliziertere
Bedingung, die wir hier nicht angeben.
Beispiele:
a) Wir betrachten das einfache Beispiel .
Die Näherungsbrüche sind
,
und
.
Die Nebennäherungsbrüche für
sind
,
,
,
(größer als
)
und für
ist es der Bruch
(zwischen
und
).
b) Für die Kreiszahl
lauten die ersten Näherungsbrüche
,
,
und
.
Die Nebennäherungsbrüche sind für
die Brüche
,
,
,
,
,
.
Sie bilden eine fallende Folge und die letzten drei sind beste Näherungen
1. Art. (Die ersten drei sind weiter entfernt von
als der Näherungsbruch
).
Für
findet man die Nebennäherungsbrüche
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Diese
Brüche bilden eine steigende Folge und die letzten sieben sind beste Näherungen
1. Art.
In der Abbildung rechts sind diese (Neben-) Näherungsbrüche illustriert: Auf
der -Achse
ist
gegen
auf der
-Achse
abgetragen. Außer den Näherungen von unten (rot) und von oben (blau) enthält die
Graphik noch die Schranke
,
deren Bedeutung im nächsten Abschnitt klar wird. [9] Gut
zu sehen ist, dass nur die zweite Hälfte der Nebennäherungsbrüche für
eine bessere Näherung liefert als
.
Außerdem sieht man, dass die Näherung durch
außergewöhnlich gut ist (Grund dafür: Der nächste Teilnenner ist mit
sehr groß).
Sätze über quadratische Approximierbarkeit
In diesem Abschnitt stellen wir Ergebnisse vor, die zum Thema „Diophantische Approximation“ überleiten.
Aus Gleichung (3) folgt wegen
Zu jeder irrationalen Zahl
gibt es unendlich viele Brüche
mit [10]
Umgekehrt gilt für jede reelle Zahl :
Satz (Legendre):
Erfüllt ein Bruch
die Ungleichung
so ist
ein Näherungsbruch von
.
Diese Ungleichung wird jedoch nicht von jedem Näherungsbruch erfüllt. Es gilt aber:
Satz (Theodor Vahlen,
1895):
Von jeweils zwei aufeinanderfolgenden Näherungsbrüchen der reellen Zahl
erfüllt mindestens einer die Ungleichung
Insbesondere gibt es auch hier für irrationales
unendlich viele Brüche mit dieser Eigenschaft.
Bezieht man drei Näherungsbrüche in die Auswahl ein, so gilt sogar:
Satz (Émile
Borel, 1903):
Von jeweils drei aufeinanderfolgenden Näherungsbrüchen der reellen Zahl
erfüllt mindestens einer die Ungleichung
Insbesondere gibt es für irrationales
unendlich viele Brüche mit dieser Eigenschaft.
Man könnte angesichts dieser Ergebnisse vermuten, dass man die Bedingung durch Einbeziehen von vier oder mehr aufeinanderfolgenden Näherungsbrüche weiter verschärfen kann. Dies ist aber nicht der Fall:
Satz (Adolf Hurwitz,
1891,
siehe auch Satz
von Hurwitz): Sei
die goldene
Zahl. Dann gibt es für jede reelle Zahl
mit
nur endliche viele Brüche
mit
Eine Verschärfung lässt sich nun nur erreichen, wenn man die zu
äquivalenten Zahlen ausschließt:
Satz (Hurwitz, 1891):
Für alle irrationalen Zahlen ,
die nicht äquivalent zu
sind, gibt es unendlich viele Brüche
mit
|
|
|
(5) |
|
|
Durch weiteres Ausschließen von Äquivalenzklassen kann man die Konstante
weiter vergrößern. Die dabei auftretenden Werte
bilden das sogenannte Lagrange-Spektrum. Sie konvergieren gegen die
Zahl 3 und sind mit den Markoff-Zahlen
verwandt.
Eigenschaften fast aller irrationalen Zahlen

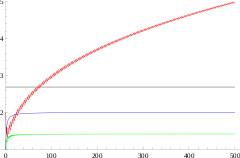
Rot:
Blau:
Grün: ∛2 (Kubikwurzel aus 2).
Schwarze Linie: Chintschin-Konstante
Rot:
Blau: √2 (Wurzel 2),
Grün: √3 Wurzel 3).
Schwarze Linie: Chintschin-Konstante
Chintschin-Konstante
Die sogenannte metrische Kettenbruchtheorie beschäftigt sich mit Eigenschaften, die typische reelle Zahlen haben. Sie geht auf den gleichnamigen Artikel von Alexander Chintschin in der Zeitschrift Compositio Mathematica aus dem Jahr 1935 zurück, aber auch Gauß beschäftigte sich schon mit ähnlichen Themen.[11] Typisch ist hier im maßtheoretischen Sinn zu verstehen: Man formuliert Eigenschaften, die, bis auf eine Nullmenge, alle reellen Zahlen besitzen. In diesem Fall sagt man, dass fast alle reellen Zahlen diese Eigenschaft haben.
Das Ergebnis von Chintschin lautet: Für fast alle reellen Zahlen konvergiert
für
gegen die Konstante
(Folge A002210 in OEIS).
Das geometrische Mittel der Teilnenner fast jeder reellen Zahl konvergiert also gegen eine feste Konstante. Zu den Ausnahmen gehören alle rationalen Zahlen, da sie nur endlich viele Teilnenner besitzen – aber sie bilden eben auch nur eine Nullmenge der reellen Zahlen.
Es ist nicht bekannt, ob diese sogenannte Chintschin-Konstante rational, algebraisch irrational oder transzendent ist.
Die Kettenbruchentwicklungen von Zahlen, für die der Grenzwert nicht
existiert oder ungleich der Chintschin-Konstante ist, sind meist besonders
regelmäßig. Dies gilt für reelle Lösungen quadratischer Gleichungen (periodische
Kettenbruchentwicklung, z.B. die Quadratwurzel von ),
die Eulersche Zahl
(Muster wurde weiter oben erwähnt) und beispielsweise alle Zahlen der Form
oder
(
).
Rechts sind Diagramme zu den Graphen
der Funktion
für je drei Beispiele zu sehen.
Vergleich von Kettenbruchdarstellung und Dezimaldarstellung
Der Satz von Lochs besagt folgendes: Für fast jede reelle Zahl
zwischen
und
bekommt man auf lange Sicht für jedes weitere Glied eines Kettenbruchs
-viele
gültige Dezimalstellen.
Damit ist die Darstellung mit Kettenbrüchen (für fast alle Zahlen) nur leicht
effizienter als die Dezimaldarstellung. Die Lochs-Konstante ist mit der Lévy-Konstante
verwandt (sie ist das Doppelte des Zehner-Logarithmus der Lévy-Konstante).
Literatur
- Oskar Perron: Die Lehre von den Kettenbrüchen.1. Auflage in einem Band. Teubner, 1913
- Oskar Perron: Irrationalzahlen. Göschens Lehrbücherei, Band 1. Walter de Gruyter, Berlin/Leipzig 1921
- Alexander J. Chintschin: Kettenbrüche. Teubner, Leipzig 1956, oder Continued Fractions. Dover Publications, 1997 (russ. Original 1935)
- Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-76490-8.
Anmerkungen
- ↑ Dass dieser Kettenbruch gleich der Quadratwurzel von 2 ist, wird im Abschnitt Periodische Kettenbrüche gezeigt.
- ↑ Die Angabe des relativen Fehlers ist hier nicht sinnvoll, da sich die Approximationseigenschaften einer Zahl nicht durch Addition von ganzen Zahlen ändern.
- ↑ Leonhard Euler und Chr. Goldbach, Briefwechsel.
- ↑
In der älteren Literatur werden
und
oft vertauscht, sodass die Teilnenner
heißen.
- ↑
Außer den hier angegebenen Schreibweisen gibt es
noch
(zum Beispiel in Conway, Guy: The book of numbers. Springer, 1996),
(z.B. im Buch von Niven/Zuckerman) sowie
(z.B. in Donald Knuth: >The Art of Computer Programming. (Band 2), Addison Wesley, 1997).
- ↑
Das wäre zum Beispiel nicht der Fall, wenn als
Teilnenner beliebige positive reelle Zahlen zugelassen wären. In diesem Fall
gilt: Der Kettenbruch
konvergiert genau dann, wenn die Summe
divergiert.
- ↑
Als Quelle siehe Eulers De usu novi algorithmi in problemate Pelliano
solvendo. Ganz unten erkennt man auch die Zahl
. Die Kettenbruchentwicklung ihrer Quadratwurzel hat Periode
:
und Euler rechnet sie als nächstes Beispiel aus. Einige Seiten später findet man eine komplette Liste der periodischen Kettenbrüche für
bis 120.
- ↑
Es gibt noch einen Ausnahmefall für rationale
Zahlen
, der aber vermieden werden kann, wenn man nur solche Kettenbrüche erlaubt, deren letzter Teilnenner größer als
ist. Es handelt sich um
. Diese kann man als
oder als
schreiben. Im letzten Fall ist
und dieser Näherungsbruch hat den gleichen Abstand zu
wie der 0-te Näherungsbruch
. Siehe Hardy/Wright, Seite 194.
- ↑ Genauer formuliert müsste man natürlich sagen, dass die Graphik zusätzlich noch den Logarithmus dieser Schranke enthält.
- ↑ Siehe auch die ähnliche Aussage im Artikel Dirichletscher Approximationssatz.
- ↑
Der Satz von Gauß-Kusmin betrifft die
Wahrscheinlichkeitsverteilung der Teilnenner reeller Zahlen (R. O.
Kusmin, 1928, außerdem Paul
Lévy, 1929). Es gilt nämlich für alle natürlichen Zahlen
: Das Maß von
konvergiert für
gegen
. Für
beträgt der Grenzwert ungefähr 41 %, für
ungefähr 17 %. Siehe hierzu das Buch von Chintschin.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 31.07. 2022