
Irrationale Zahl
.svg.png)
Eine irrationale Zahl ist eine reelle Zahl, die keine rationale Zahl ist. Kennzeichen einer irrationalen Zahl ist, dass sie nicht als Quotient zweier ganzer Zahlen darstellbar ist. In der Dezimalschreibweise werden irrationale Zahlen mit einer nicht periodischen, unendlichen Anzahl von Dezimalstellen dargestellt (z.B. 0,10110111011110…), d.h., sie sind unendliche nichtperiodische Dezimalbrüche.
Bekannte irrationale Zahlen sind die Eulersche
Zahl
und die Kreiszahl
,
die darüber hinaus transzendent
sind. Auch die Quadratwurzel
aus Zwei
und das Teilungsverhältnis
des Goldenen
Schnitts sind irrationale Zahlen.
Definition
Eine reelle Zahl heißt
irrational, wenn sie nicht als Bruch zweier ganzer
Zahlen dargestellt werden kann; sie kann nicht als
mit
geschrieben werden.
Im Gegensatz zu rationalen Zahlen, die als endliche oder periodische Dezimalzahlen dargestellt werden können, sind irrationale Zahlen solche, deren Dezimaldarstellung weder abbricht, noch periodisch ist.
Es gibt zwei Arten von Irrationalzahlen:
- Algebraische
Zahlen, etwa
oder quadratische Wurzeln aus Nicht-Quadratzahlen wie
- Transzendente
Zahlen, etwa die Kreiszahl
oder die Eulersche Zahl
Die Menge der irrationalen Zahlen lässt sich als Differenzmenge
schreiben, wobei
die Menge der reellen Zahlen und
die Menge der rationalen Zahlen bezeichnet.
Entdeckung der Irrationalität
Den ersten Beweis für irrationale Größenverhältnisse gab es in der griechischen Antike im 5. Jahrhundert v.Chr. bei den Pythagoreern. Definitionen für irrationale Zahlen, die den heutigen Ansprüchen an Exaktheit genügen, finden sich bereits in den Elementen von Euklid. Übersetzungen in die heutige Sprache der Mathematik gaben zuerst Karl Weierstraß und Richard Dedekind an.
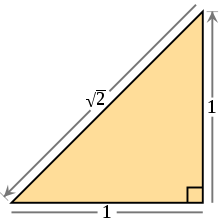
Hat man ein Quadrat mit der Seitenlänge
und berechnet dessen Diagonale
,
folgt aus dem Satz
des Pythagoras
also
.
Die positive Lösung dieser Gleichung bezeichnet man heute mit
.
Für griechische Mathematiker stellte sich die Frage, ob sich die Länge dieser
Diagonale exakt durch ein Verhältnis zweier natürlicher
Zahlen
und
,
also einen Bruch
,
darstellen lässt. Schon Euklid
bewies durch Widerspruch, dass dies unmöglich ist, sein Beweis wird heute
noch in der Schule gelehrt. Ob die Entdeckung der Irrationalität durch Anwendung
des pythagoräischen Lehrsatzes auf ein Quadrat erfolgte oder, wie Kurt von Fritz meinte,
durch stetige Teilung am Pentagramm,
ist unbekannt.
Die ältere wissenschaftsgeschichtliche Forschung nahm an, dass die Entdeckung der Irrationalität zu einer Grundlagenkrise der damaligen griechischen Mathematik oder der pythagoreischen Zahlenlehre führte. Man sei nämlich vorher von der Grundvoraussetzung ausgegangen, dass alles durch ganzzahlige Zahlverhältnisse ausdrückbar sei, und die Widerlegung dieser Ansicht habe das Weltbild der Pythagoreer erschüttert. Damit wurde eine antike Legende in Zusammenhang gebracht, wonach der Pythagoreer Hippasos von Metapont im 5. Jahrhundert v.Chr. durch die schriftliche Bekanntmachung dieser Entdeckung einen Geheimnisverrat begangen habe und später im Meer ertrunken sei, was als göttliche Strafe gedeutet wurde. Ein Teil der Quellen überliefert, Hippasos selbst habe die Irrationalität entdeckt. Wissenschaftshistoriker gehen heute davon aus, dass es eine solche Krise nicht gegeben hat und die Irrationalität nicht als Geheimnis betrachtet wurde. Eine mögliche Erklärung der Verratslegende ist, dass sie durch ein Missverständnis entstand, weil das griechische Eigenschaftswort, das für „irrational“ (im mathematischen Sinn) verwendet wurde, zugleich die Bedeutungen „unsagbar“ und „geheim“ hatte. Tatsache ist aber auch, dass sich die griechische Mathematik in der Zeit nach Hippasos grundlegend veränderte.
Zahlen, deren Irrationalität bewiesen ist
- Schon der Pythagoreer Archytas
von Tarent bewies die Irrationalität von
für natürliche Zahlen
. Der Beweis für den Fall
(
) ist in Euklids Elementen überliefert (Euklids Beweis der Irrationalität der Wurzel aus 2). Den Satz des Archytas verallgemeinerte Euklid selbst in seiner Musiktheorie, in der er die Irrationalität beliebiger Wurzeln
bewies.
- Eine weitere wichtige quadratische Irrationalität ist der Goldene Schnitt
.
- Die Eulersche
Zahl
ist irrational. Dies hat Leonhard Euler 1737 bewiesen. Ihre Transzendenz wurde 1873 von Charles Hermite bewiesen.
- 1761 bewies Johann
Heinrich Lambert die Irrationalität der Kreiszahl
, ihre Transzendenz wurde 1882 von Ferdinand von Lindemann bewiesen.
- Die nichtganzzahligen Nullstellen eines normierten Polynomes
mit ganzzahligen Koeffizienten sind irrational. Insbesondere sind die Quadratwurzeln aus Nichtquadratzahlen
irrational.
- Im Jahr 1979 bewies Roger
Apéry die Irrationalität der Apéry-Konstante
.
ist transzendent (siehe Satz von Gelfond-Schneider).
ist transzendent, dies hat Carl Ludwig Siegel bewiesen.
- Die Transzendenz von
(wie auch von
) folgt aus dem Satz von Gelfond-Schneider.
- Die lemniskatische
Konstante
ist transzendent (Theodor Schneider, 1937).
- Im Jahr 1963 bewies Solomon W. Golomb die Irrationalität der Summe der Reziproken aller Fermat-Zahlen. Es gilt:
Zahlen, deren Irrationalität vermutet wird
Die Irrationalität der Zahlen
wird vermutet, ist aber noch nicht bewiesen. Man kann aber leicht sehen, dass
mindestens eine von einer beliebigen Paarbildung irrational sein muss. Dies gilt
allgemein für zwei beliebige transzendente Zahlen
und
.
Für kein einziges Paar ganzer, von
verschiedener Zahlen
und
ist bekannt, ob
irrational ist. Bekannt ist jedoch, dass im Falle der Existenz rationaler
Linearkombinationen der Wert
einen konstanten Wert annimmt.
Weiterhin ist unbekannt, ob ,
,
,
,
,
die Catalansche
Konstante
oder die Eulersche
Konstante
irrational sind. Es erscheint jedoch sinnvoll, dies zu vermuten.
Die Überabzählbarkeit der irrationalen Zahlen
Wie das erste Diagonalargument von Cantor zeigt, ist die Menge der rationalen Zahlen abzählbar. Es gibt also eine Folge rationaler Zahlen, die jede rationale Zahl enthält. Cantors zweites Diagonalargument beweist, dass es überabzählbar viele reelle Zahlen gibt. Das bedeutet gleichzeitig, dass es überabzählbar viele irrationale Zahlen geben muss;[2] denn andernfalls wären die reellen Zahlen als Vereinigung zweier abzählbarer Mengen selbst abzählbar.
Cantor hat weiter gezeigt, dass auch die Menge der algebraischen Zahlen, wozu alle Wurzelausdrücke gehören, noch abzählbar ist. Darüber hinaus gilt, dass die algebraische Hülle jeder abzählbaren Teilmenge der reellen oder komplexen Zahlen (solche Mengen können insbesondere aus transzendenten Zahlen bestehen) ebenfalls abzählbar ist, also sicher nicht alle reellen Zahlen enthält.
Literatur
- Tom Müller: Irrationalitätsbeweise. Heldermann Verlag, Lemgo 2014, ISBN 978-3-88538-125-9.
Anmerkungen
- ↑
Für die Menge der irrationalen Zahlen gibt es
kein eigenes Kürzel, aber eine Zahl ist genau dann irrational, wenn sie reell
und nicht rational ist. Es gilt also:
Menge der irrationalen Zahlen := Menge der reellen Zahlen ohne Menge der rationalen Zahlen. - ↑ Das bedeutet insbesondere, dass sich nicht alle irrationalen Zahlen „darstellen“ oder „berechnen“ lassen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.11. 2024