Eulersche Formel

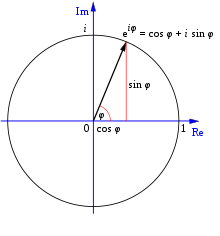
Veranschaulichung am Einheitskreis in der komplexen Zahlenebene

Dreidimensionale Darstellung der eulerschen Formel

Die nach Leonhard Euler benannte eulersche Formel bzw. Eulerformel, in manchen Quellen auch eulersche Relation, ist eine Gleichung, die eine grundsätzliche Verbindung zwischen den trigonometrischen Funktionen und den komplexen Exponentialfunktionen mittels komplexer Zahlen darstellt.

Eulersche Formel

Die eulersche Formel bezeichnet die für alle $y\in {\mathbb R}$ gültige Gleichung

$\mathrm {e} ^{\mathrm {i} \,y}=\cos \left(y\right)+\mathrm {i} \,\sin \left(y\right)$ ,

wobei die Konstante $\mathrm {e}$ die eulersche Zahl (Basis der natürlichen Exponentialfunktion bzw. des natürlichen Logarithmus) und die Einheit $\mathrm {i}$ die imaginäre Einheit der komplexen Zahlen bezeichnen.

Als Folgerung aus der eulerschen Formel ergibt sich für alle $z={x+\mathrm {i} y}\in \mathbb {C}$ die Gleichung

$\mathrm {e} ^{z}=\mathrm {e} ^{x+\mathrm {i} y}=\mathrm {e} ^{x}\cdot \mathrm {e} ^{\mathrm {i} y}=\mathrm {e} ^{x}\cdot \left(\cos \left(y\right)+\mathrm {i} \,\sin \left(y\right)\right)$ .

Herleitung mittels Reihenentwicklung

Animation der Herleitung der Eulerschen Formel

Die eulersche Formel lässt sich aus den maclaurinschen Reihen der Funktionen $\mathrm {e} ^{y},\sin y$ und $\cos y$ , $y\in \mathbb {R}$ , herleiten

${\begin{aligned}\mathrm {e} ^{\mathrm {i} y}&=1+\mathrm {i} y+{(\mathrm {i} y)^{2} \over 2!}+{(\mathrm {i} y)^{3} \over 3!}+{(\mathrm {i} y)^{4} \over 4!}+\dots \\&=\left(1-{\frac {y^{2}}{2!}}+{\frac {y^{4}}{4!}}-\dots \right)+\mathrm {i} \cdot \left(y-{\frac {y^{3}}{3!}}+{\frac {y^{5}}{5!}}-\dots \right)\\&=\cos(y)+\mathrm {i} \cdot \sin(y)\end{aligned}}$

Die Umformungen basieren auf $i^{2}=-1.$

Eulersche Identität

Animation der Approximation von $\mathrm {e} ^{\mathrm {i} \pi }$ durch den Ausdruck $\lim _{n\rightarrow \infty }(1+\mathrm {i} \pi /n)^{n}$ . Die Punkte stellen jeweils für ein die Werte $(1+\mathrm {i} \pi /n)^{j}$ mit $j=0,\dots ,n$ dar.

Für $y=\pi$ ergibt sich aus der eulerschen Formel die sogenannte eulersche Identität

$\mathrm {e} ^{\mathrm {i} \,\pi }={-1}$ ,

die einen einfachen Zusammenhang zwischen vier der bedeutendsten mathematischen Konstanten herstellt: der eulerschen Zahl $\mathrm {e}$ , der Kreiszahl $\mathrm {\pi }$ , der imaginären Einheit $\mathrm {i}$ sowie der reellen Einheit . Die folgende umgeformte Variante der Gleichung wird bisweilen – obwohl komplizierter – bevorzugt, da in ihr mit der Null noch eine weitere mathematisch bedeutende Konstante hinzukommt:

$\mathrm {e} ^{\mathrm {i} \,\pi }+1=0$ .

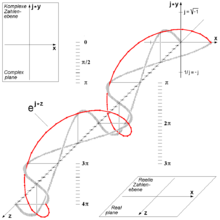
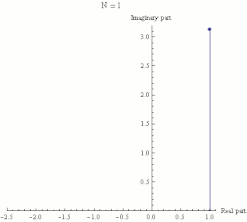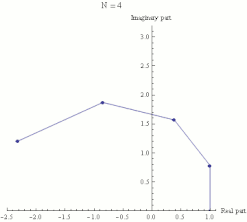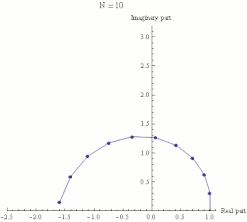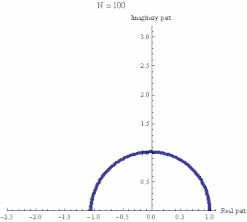
Erweitert man die Definition des Zahlenwerts von $\mathrm {e} ^{z}$ als Grenzwert $\textstyle \lim _{n\rightarrow \infty }(1+z/n)^{n}$ auf die komplexe Zahlenebene mit $z\in {\mathbb C}$ , so ergibt sich dementsprechend für $z=\mathrm {i} \pi$ der Wert {-1} . Die nebenstehende Animation zeigt die zu einem Streckenzug in der komplexen Ebene verbundenen Zwischenergebnisse der Berechnung des Ausdrucks $(1+\mathrm {i} \pi /n)^{n}$ : Sie veranschaulicht, dass dieser Streckenzug für wachsendes die Form eines Kreisbogens annimmt, dessen linkes Ende sich tatsächlich der Zahl {-1} auf der reellen Achse nähert.

Beziehung zwischen Exponentialfunktionen und trigonometrischen Funktionen

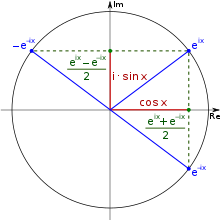
Beziehung zwischen Sinus, Kosinus und Exponentialfunktion

Formulierung

Die eulersche Formel ist ein zentrales Bindeglied zwischen Analysis und Trigonometrie:

$\sin x={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }},\quad \cos x={\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}$ .

Herleitung

Sinus und Kosinus ergeben sich aus Realteil und Imaginärteil der komplexen Exponentialfunktion.

Den Realteil erhält man, indem man eine komplexe Zahl mit der Konjugierten ${\bar {z}}$ addiert und durch zwei dividiert:

$\cos(x)=\mathrm {Re} (\mathrm {e} ^{\mathrm {i} x})={\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}$ .

Den Imaginärteil erhält man, indem man ${\frac {z-{\bar {z}}}{2\mathrm {i} }}$ berechnet:

$\sin(x)=\mathrm {Im} (\mathrm {e} ^{\mathrm {i} x})={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}$ .

Erläuterung

Die Eulerformel erlaubt eine völlig neue Sicht auf die trigonometrischen Funktionen, da die in der herkömmlichen Trigonometrie allein mit reellen Argumenten verwendeten Funktionen Sinus und Kosinus nun auch noch eine Bedeutung in der komplexen Analysis erhalten.

Die Formeln für Real- und Imaginärteil ergeben sich durch:

${\begin{aligned}\mathrm {Re} (a+b\,\mathrm {i} )={\frac {z+{\bar {z}}}{2}}={\frac {(a+b\mathrm {i} )+(a-b\,\mathrm {i} )}{2}}={\frac {2a}{2}}=a,\\\mathrm {Im} (a+b\,\mathrm {i} )={\frac {z-{\bar {z}}}{2\mathrm {i} }}={\frac {(a+b\,\mathrm {i} )-(a-b\,\mathrm {i} )}{2\mathrm {i} }}={\frac {2b\mathrm {i} }{2\mathrm {i} }}=b\end{aligned}}$

Eine Folge der Verbindung von trigonometrischen Funktionen und Exponentialfunktion aus der Eulerformel ist der Moivresche Satz (1730).

Hyperbelfunktionen

Versieht man die Sinus und Kosinus mit imaginären Argumenten, wird dadurch eine Brücke zu den Hyperbelfunktionen geschlagen:

$\sin(\mathrm {i} y)={\mathrm {e} ^{-y}-\mathrm {e} ^{y} \over 2\mathrm {i} }=\mathrm {i} \,{\frac {\mathrm {e} ^{y}-\mathrm {e} ^{-y}}{2}}=\mathrm {i} \,\sinh(y)$

$\cos(\mathrm {i} y)={\frac {\mathrm {e} ^{-y}+\mathrm {e} ^{y}}{2}}={\frac {\mathrm {e} ^{y}+\mathrm {e} ^{-y}}{2}}=\cosh(y)$

Wie zu sehen, entsprechen die beiden erhaltenen Funktionen genau den Definitionen des Sinus hyperbolicus und Kosinus hyperbolicus.

Weitere Anwendungen

Zeigerdarstellung einer Wechselspannung in der komplexen Ebene

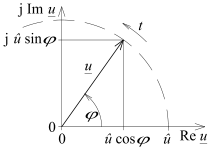
Ausgehend davon findet die eulersche Formel auch zur Lösung zahlreicher anderer Probleme Anwendung, etwa bei der Berechnung der Potenz $\mathrm {i} ^{\mathrm {i} }$ der imaginären Einheit mit sich selbst. Obwohl das erhaltene Resultat mehrdeutig ist, bleiben alle Einzellösungen im reellen Bereich mit einem Hauptwert von $\mathrm {i} ^{\mathrm {i} }=\mathrm {e} ^{-\pi /2}=0{,}207\,879\dots$

Eine praktisch wichtige Anwendung der eulerschen Formel findet sich im Bereich der Wechselstromtechnik, namentlich bei der Untersuchung und Berechnung von Wechselstromkreisen mit Hilfe komplexer Zahlen.

Geschichte

Die eulersche Formel erschien erstmals 1748 in Leonhard Eulers zweibändiger Introductio in analysin infinitorum unter der Prämisse, dass der Winkel eine reelle Zahl ist. Diese Einschränkung jedoch erwies sich bald als überflüssig, denn die eulersche Formel gilt gleichermaßen für alle reellen wie komplexen Argumente. Dies ergibt sich aus der eulerschen Formel mit reellem Argument in Verbindung mit dem Identitätssatz für holomorphe Funktionen.

Zuvor hat Roger Cotes 1714 einen fehlerhaften mathematischen Zusammenhang veröffentlicht, welcher der eulerschen Formel ähnelt.

In moderner Notation sieht er folgendermaßen aus:

$\mathrm {i} \cdot r\cdot \ln(\cos(\varphi )+\mathrm {i} \sin(\varphi ))=r\cdot \varphi \quad {\text{(sic!)}}$ ,

wobei ein im Koordinatenursprung fixierter Kreis mit Radius und ein Winkel $\varphi$ zwischen x-Achse und einem Strahl, der den Ursprung schneidet, betrachtet werden.

Die imaginäre Einheit $\mathrm {i}$ müsste auf der anderen Seite der Gleichung stehen.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de