Kreis

Ein Kreis ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises, er ist eine positive reelle Zahl. Der Kreis gehört zu den klassischen und grundlegenden Objekten der euklidischen Geometrie.
Schon die alten Ägypter und Babylonier versuchten, den Flächeninhalt des Kreises näherungsweise zu bestimmen. Besonders in der griechischen Antike war der Kreis wegen seiner Vollkommenheit von großem Interesse. Beispielsweise versuchte Archimedes erfolglos, mit den Werkzeugen Zirkel und Lineal den Kreis in ein Quadrat mit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können. Ein solches Verfahren zur Berechnung des Flächeninhalts nennt man die Quadratur des Kreises. Erst 1882 konnte Ferdinand von Lindemann durch Nachweis einer besonderen Eigenschaft der Kreiszahl zeigen, dass diese Aufgabe unlösbar ist.
Worterklärungen
Kreisflächen
Nach der eingangs genannten Definition ist ein Kreis eine Kurve, also ein eindimensionales Gebilde, und keine zweidimensionale Fläche. Da das Wort „Kreis“ aber oft ungenau auch für die eingeschlossene Fläche benutzt wird, verwendet man zur Verdeutlichung häufig die Begriffe Kreislinie, Kreisrand oder Kreisperipherie anstatt Kreis – im Gegensatz zur Kreisfläche oder Kreisscheibe. Mathematiker unterscheiden dann noch zwischen der abgeschlossenen Kreisfläche oder -scheibe und der offenen (oder dem Kreisinneren), je nachdem ob die Kreislinie dazugehört oder nicht.
Bogen, Sehne, Sektor, Segment und Ring
Eine zusammenhängende Teilmenge des Kreises (also der Kreislinie) ist ein Kreisbogen. Eine Verbindungsstrecke von zwei Punkten auf der Kreislinie bezeichnet man als Kreissehne. Zu jeder Sehne gehören zwei Kreisbögen. Die längsten Kreissehnen sind diejenigen, die durch den Mittelpunkt verlaufen, also die Durchmesser. Die zugehörigen Kreisbögen heißen Halbkreise. Ist die Kreissehne kein Durchmesser, so sind die Kreisbögen unterschiedlich lang.
Ein Kreissektor (Kreisausschnitt) ist eine Fläche, die von zwei Radien und einem dazwischen liegenden Kreisbogen begrenzt wird. Bilden die zwei Radien einen Durchmesser, wird der Sektor auch als Halbkreis bezeichnet.
Kreissegmente (Kreisabschnitte) werden von einem Kreisbogen und einer Kreissehne eingeschlossen.
Ein Kreisring entsteht, wenn man aus einem Kreis einen kleineren Kreis mit demselben Mittelpunkt herausschneidet.
Tangente, Passante und Sekante
Für die Lage einer Geraden in Bezug auf einen gegebenen Kreis gibt es drei Möglichkeiten:
- Ist der Abstand zwischen Mittelpunkt und Gerade kleiner als der Kreisradius, so haben Kreis und Gerade zwei (verschiedene) Schnittpunkte und man nennt die Gerade Sekante (lateinisch secare = schneiden). Manchmal bezeichnet man den Spezialfall einer Sekante, die durch den Mittelpunkt eines Kreises verläuft, als Zentrale.
- Stimmt der Abstand des Mittelpunkts zu der Geraden mit dem Radius überein, so gibt es genau einen gemeinsamen Punkt. Man sagt, dass die Gerade den Kreis berührt, und nennt die Gerade eine Tangente (lateinisch tangere = berühren). Eine Tangente steht im Berührpunkt senkrecht (orthogonal, normal) zum entsprechenden Radius.
- Wenn der Abstand des Kreismittelpunkts von der Geraden größer ist als der Kreisradius, dann haben Kreis und Gerade keinen Punkt gemeinsam. In diesem Fall bezeichnet man die Gerade als Passante. Diese Bezeichnung hat keinen unmittelbaren lateinischen Ursprung, sondern wurde wohl nach franz. oder ital. passante = Vorbeigehende gebildet. Die lat. Wurzel ist passus = Schritt.
Formale Definition

In einer Ebene
ist ein Kreis
mit Mittelpunkt
und Radius
die Punktmenge
Dabei ist der Radius
eine positive reelle Zahl, und
bezeichnet die Länge der Strecke
.
Der doppelte Radius heißt Durchmesser
und wird oft mit
bezeichnet. Radius
und Durchmesser
sind durch die Beziehungen
oder
miteinander verknüpft.
Manchmal wird auch jede Strecke, die den Mittelpunkt mit einem Punkt
auf der Kreislinie verbindet, als Radius bezeichnet, und jede Strecke,
die durch den Mittelpunkt geht, und deren beide Endpunkte auf der Kreislinie
liegen, als Durchmesser. Bei dieser Sprechweise ist die Zahl
die Länge jedes Radius und die Zahl
die Länge jedes Durchmessers.
Die offene Kreisfläche ist formal definiert als die Punktmenge
die abgeschlossene Kreisscheibe als
Geschichte

Zeit der Ägypter und Babylonier


Der Kreis gehört neben dem Punkt
und der geraden
Linie zu den ältesten Elementen der vorgriechischen Geometrie. Schon vor
viertausend Jahren beschäftigten sich die Ägypter mit ihm in ihren Studien zur
Geometrie. Sie konnten den Flächeninhalt
eines Kreises näherungsweise bestimmen, indem sie vom Durchmesser d ein
Neuntel seiner Länge abzogen und das Ergebnis mit sich selbst multiplizierten.
Sie rechneten also
und bestimmten so näherungsweise (mit einer Abweichung von nur etwa +0,6 %) den Flächeninhalt einer Kreisfläche. Diese Näherung wurde in der altägyptischen Abhandlung Papyrus Rhind gefunden, sie lässt sich erhalten, wenn man den Kreis durch ein unregelmäßiges Achteck annähert.
Die Babylonier (1900 bis 1600 vor Christus) benutzten eine ganz andere
Methode, um den Flächeninhalt der Kreisscheibe zu berechnen. Im Gegensatz zu den
Ägyptern gingen sie vom Kreisumfang
aus, den sie als dreimal den Kreisdurchmesser
schätzten. Der Flächeninhalt wurde dann auf ein Zwölftel des Quadrates des Umfanges
geschätzt, also
mit einer Abweichung von −4,5 % ein deutlich schlechteres Ergebnis.
Die Babylonier beschäftigten sich aber auch schon mit Kreissegmenten. Sie konnten die Länge der Sehne oder die Höhe des Kreissegments (die senkrecht auf der Sehnenmitte stehende Strecke zwischen Sehne und Umfang) berechnen. Damit begründeten sie die Sehnengeometrie, die später von Hipparch weiterentwickelt wurde und die Claudius Ptolemaios an den Anfang seines astronomischen Lehrbuches Almagest stellte.
Antike
.jpg)
Die Griechen werden meist als die Begründer der Wissenschaft von der Natur angesehen. Als der erste bedeutende Philosoph dieser Zeit, der sich mit Mathematik beschäftigte, gilt Thales von Milet (624–546 v.Chr.). Er brachte Wissen über die Geometrie aus Ägypten mit nach Griechenland, wie zum Beispiel die Aussage, dass der Durchmesser den Kreis halbiert. Andere Aussagen zur Geometrie wurden von Thales selbst aufgestellt. Der heute nach Thales benannte Satz besagt, dass Peripheriewinkel im Halbkreis rechte Winkel sind. Insbesondere war Thales der erste, bei dem der Begriff des Winkels auftrat.
Die erste bekannte Definition des Kreises geht auf den griechischen Philosophen Platon (428/427–348/347 v.Chr.) zurück, die er in seinem Dialog Parmenides formulierte:
„Rund ist doch wohl das, dessen äußerste Teile überall vom Mittelpunkt aus gleich weit entfernt sind.“
Zirka 300 Jahre vor Christus lebte der griechische Mathematiker Euklid von Alexandria. Über ihn selbst ist wenig bekannt, aber sein Werk im Bereich der Geometrie war beachtlich. Sein Name ist heute noch in Zusammenhängen wie euklidischer Raum, euklidische Geometrie oder euklidische Metrik in Gebrauch. Sein wichtigstes Werk waren Die Elemente, eine dreizehnbändige Abhandlung, in der er die Arithmetik und Geometrie seiner Zeit zusammenfasste und systematisierte. Er folgerte die mathematischen Aussagen aus Postulaten und begründete damit die euklidische Geometrie. Der dritte Band der Elemente beschäftigte sich mit der Lehre über den Kreis.
Von Archimedes, der vermutlich zwischen 287 v.Chr. und 212 v.Chr. auf Sizilien lebte, ist eine ausführliche Abhandlung mit dem Titel Kreismessung überliefert. Er bewies in dieser Arbeit, dass der Flächeninhalt eines Kreises gleich dem Flächeninhalt eines rechtwinkligen Dreiecks mit dem Kreisradius als der einen und dem Kreisumfang als der anderen Kathete ist. Der Flächeninhalt des Kreises lässt sich also als ½ · Radius · Umfang angeben. Mit dieser Erkenntnis führte er das Problem der Quadratur des Kreises auf die Frage der Konstruierbarkeit des Umfangs aus dem vorgegebenen Radius zurück.
In seiner Abhandlung Kreismessung konnte Archimedes ebenfalls zeigen, dass der Umfang eines Kreises größer als 310/71 und kleiner als 31/7 des Durchmessers ist. Für praktische Zwecke wird diese Näherung 22/7 (~ 3,143) heute noch verwendet.
Aus diesen beiden Aussagen folgert man, dass sich der Flächeninhalt eines Kreises zum Quadrat seines Durchmessers nahezu wie 11/14 verhält. Euklid war bereits bekannt, dass sich der Flächeninhalt eines Kreises proportional zum Quadrat seines Durchmessers verhält. Archimedes gibt hier eine gute Näherung der Proportionalitätskonstante an.
In einer weiteren Arbeit Über Spiralen beschreibt Archimedes die Konstruktion der später nach ihm benannten archimedischen Spirale. Mit dieser Konstruktion war es Archimedes möglich, den Umfang eines Kreises auf einer Geraden abzutragen. Auf diese Weise konnte nun der Flächeninhalt eines Kreises exakt bestimmt werden. Jedoch kann diese Spirale nicht mit Zirkel und Lineal konstruiert werden.
Apollonios von Perge lebte zirka 200 Jahre vor Christus. In seiner Kegelschnittlehre Konika fasste er unter anderem die Ellipse und den Kreis als Schnitte eines geraden Kreiskegels auf – genauso wie es heute noch in der algebraischen Geometrie definiert wird. Seine Erkenntnisse gehen auf seine Vorgänger Euklid und Aristaios (um 330 v.Chr.) zurück, deren verfasste Abhandlungen über Kegelschnitte jedoch nicht mehr überliefert sind.
Nach Apollonios ist weiterhin das apollonische Problem benannt, zu drei gegebenen Kreisen mit den euklidischen Werkzeugen Lineal und Zirkel die Kreise zu konstruieren, die die gegebenen berühren. Jedoch im Vergleich zu Euklids Elementen, die auch im Mittelalter die Grundlage der Geometrie bildeten, fanden die Werke von Apollonios zunächst nur im islamischen Bereich Beachtung. In Westeuropa erlangten seine Bücher erst im 17. Jahrhundert größere Bedeutung, als Johannes Kepler die Ellipse als die wahre Bahn eines Planeten um die Sonne erkannte.
Renaissance
In der Wissenschaftsgeschichte nennt man den Zeitraum zwischen 1400 n.Chr. und 1630 n.Chr. üblicherweise Renaissance, auch wenn der zeitliche Abschnitt nicht mit der Periodisierung etwa der Kunstgeschichte übereinstimmt. In dieser Zeit fanden Euklids Elemente wieder mehr Beachtung. Sie gehörten zu den ersten gedruckten Büchern und wurden in den darauffolgenden Jahrhunderten in vielen verschiedenen Ausgaben verlegt. Erhard Ratdolt stellte 1482 in Venedig die erste gedruckte Ausgabe der Elemente her. Eine der bedeutendsten Ausgaben von Euklids Elementen wurde von dem Jesuiten Christoph Clavius herausgegeben. Er fügte den eigentlichen Texten Euklids neben den spätantiken Büchern XIV und XV noch ein sechzehntes Buch und weitere umfangreiche Ergänzungen hinzu. Beispielsweise ergänzte er eine Konstruktion der gemeinsamen Tangenten zweier Kreise.
19. Jahrhundert

Nach Vorleistungen von Leonhard
Euler, der die eulersche
Identität aufstellte, Johann
Heinrich Lambert und Charles
Hermite konnte Ferdinand
von Lindemann 1882 beweisen, dass die Zahl
transzendent
ist. Das heißt, es gibt keine Polynomfunktion mit rationalen
Koeffizienten, für die π eine Nullstelle ist. Da jedoch schon im
17. Jahrhundert gezeigt wurde, dass die Kreiszahl
eine Nullstelle einer solchen Polynomfunktion sein müsse, damit die Quadratur des
Kreises mit Zirkel und Lineal funktioniere, wurde somit zugleich bewiesen,
dass es kein solches Verfahren geben kann.
Gleichungen
In der analytischen
Geometrie werden geometrische Objekte mit Hilfe von Gleichungen beschrieben.
Punkte in der Ebene werden dazu meist durch ihre kartesischen
Koordinaten
dargestellt und ein Kreis ist dann die Menge aller Punkte, deren Koordinaten die
jeweilige Gleichung erfüllen.
Koordinatengleichung
Der euklidische
Abstand eines Punktes
vom Punkt
berechnet sich als
Durch Quadrieren der definierenden Gleichung
ergibt sich die Koordinatengleichung
für die Punkte
auf dem Kreis mit Mittelpunkt
und Radius
.
Ausmultipliziert ergibt sich daraus:
mit
,
und
.
Ein wichtiger Spezialfall ist die Koordinatengleichung des Einheitskreises
Funktionsgleichung
Da der Kreis kein Funktionsgraph ist, lässt er sich auch nicht durch eine Funktionsgleichung darstellen. Behelfsweise kann ein Paar von Funktionsgleichungen
verwendet werden. Für den Einheitskreis vereinfacht sich dieses zu
Parameterdarstellung
Eine andere Möglichkeit, einen Kreis durch Koordinaten zu beschreiben, bietet die Parameterdarstellung (siehe auch Polarkoordinaten):
Hier werden die Koordinaten
und
durch den Parameter
ausgedrückt, der alle Werte mit
annehmen kann.
Wendet man auch diese Gleichungen speziell auf den Einheitskreis an, so erhält man:
Es ist auch eine Parameterdarstellung ohne den Rückgriff auf trigonometrische
Funktion möglich (rationale Parametrisierung), allerdings wird dabei die
gesamte Menge der reellen Zahlen als Parameterbereich benötigt und der Punkt
wird nur als Grenzwert für
erreicht.
Für den Einheitskreis ergibt sich dann:
Komplexe Darstellung
In der komplexen
Zahlenebene lässt sich der Kreis um
mit Radius
durch die Gleichung
darstellen. Mit Hilfe der komplexen Exponentialfunktion erhält man die Parameterdarstellung
Dreipunkteform einer Kreisgleichung
Die Koordinatengleichung des Kreises durch drei vorgegebene Punkte ,
die nicht auf einer Gerade liegen, ergibt sich durch Umformung der 3-Punkteform
(Beseitigung der Nenner und quadratische Ergänzung):
Kreis durch drei Punkte
Aus der Dreipunkteform und der Koordinatengleichung ergibt sich für den Kreis
durch drei vorgegebene Punkte
mit
und den Determinanten
für den Mittelpunkt
und den Radius
Liegen die drei gegebenen Punkte auf einer Geraden, so ist .
Kreisberechnung
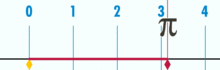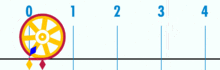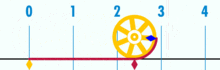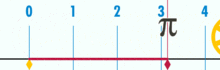
Kreiszahl
Da alle Kreise ähnlich
sind, ist das Verhältnis von Kreisumfang und Kreisdurchmesser für alle Kreise
konstant. Der Zahlenwert dieses Verhältnisses wird in der Elementargeometrie als
Definition für die Kreiszahl
verwendet. Es handelt sich hierbei um eine transzendente
Zahl, bei der sich außerdem gezeigt hat, dass sie in vielen Bereichen der
höheren Mathematik eine herausragende Bedeutung besitzt.
Umfang
Im Rahmen der Elementargeometrie ist
das Verhältnis von Kreisumfang
zu dessen Durchmesser
,
und zwar für beliebige Kreise. Somit gilt
Mit
ist der Radius des Kreises gemeint.
Kreisfläche


Der Flächeninhalt
der Kreisfläche
(lat.
area: Fläche) ist proportional zum Quadrat des Radius
bzw. des Durchmessers
des Kreises. Man bezeichnet ihn auch als Kreisinhalt.
Um die Formel für den Kreisinhalt zu erhalten, sind Grenzwert-Betrachtungen unerlässlich. Recht anschaulich ergibt sich eine solche aus der nebenstehenden Zeichnung:
Die Kreisfläche ist zerlegungsgleich mit der Fläche der rechten Figur. Diese
nähert sich bei feiner werdender Sektoreinteilung einem Rechteck an mit der
Länge
und der Breite
.
Die Flächenformel ist somit
Die Flächenformel kann zum Beispiel durch Integrieren der Kreisgleichung oder mit Hilfe der unten beschriebenen Annäherung durch regelmäßige Vielecke bewiesen werden.
Durchmesser
Der Durchmesser
eines Kreises mit Flächeninhalt
und mit Radius
lässt sich durch
berechnen.
Krümmung
Eine im Vergleich zu den bis jetzt beschriebenen Größen weniger elementare
Eigenschaft des Kreises ist die Krümmung.
Zur präzisen Definition der Krümmung werden Begriffe aus der Analysis benötigt, sie lässt
sich jedoch aufgrund der Symmetrieeigenschaften des Kreises einfach berechnen.
Anschaulich gibt die Krümmung in jedem Punkt
an, wie stark der Kreis in der unmittelbaren Umgebung des Punktes
von einer Geraden abweicht. Die Krümmung
des Kreises im Punkt
lässt sich durch
berechnen, wobei
wieder der Radius des Kreises ist. Im Gegensatz zu anderen mathematischen Kurven
hat der Kreis in jedem Punkt die gleiche Krümmung. Außer dem Kreis hat nur noch
die Gerade eine konstante Krümmung, mit
.
Bei allen anderen Kurven ist die Krümmung vom Punkt
abhängig.
Weitere Formeln
In den folgenden Formeln bezeichnet
den Sektorwinkel im Bogenmaß.
Bezeichnet
den Winkel im Gradmaß,
so gilt die Umrechnung
.
| Formeln zum Kreis | |
|---|---|
| Fläche eines Kreisringes | |
| Länge eines Kreisbogens | |
| Fläche Kreissektor | |
| Fläche eines Kreissegments | |
| Länge Kreissehne | |
| Höhe (Kreissegment) | |
Näherungen für den Flächeninhalt
Da die Kreiszahl
eine transzendente
Zahl ist, gibt es kein Konstruktionsverfahren mit Zirkel und Lineal, mit dem
man den Flächeninhalt exakt bestimmen kann. Außerdem sind transzendente Zahlen
auch irrational,
und daher hat
auch keine endliche
Dezimalbruchentwicklung, weshalb der Kreisflächeninhalt bei rationalem Radius auch
keine endliche Dezimalbruchentwicklung besitzt. Aus diesen Gründen wurden bis
heute unterschiedliche Näherungsverfahren für den Flächeninhalt und somit auch
den Umfang eines Kreises entwickelt. Manche der Näherungsverfahren, wie
beispielsweise das im Abschnitt Annäherung
durch Vielecke erläuterte Verfahren, können durch mehrfache Wiederholung
ein beliebig genaues Ergebnis liefern.
Annäherung durch Quadrate
Ein Kreis mit Radius
wird mit einem Quadrat der Seitenlänge
umschrieben. Ihm wird weiter ein Quadrat mit der Diagonalen
einbeschrieben. Der Flächeninhalt des äußeren Quadrates ist
,
der des inneren nach der Dreiecksflächenformel
und der Mittelwert
ist somit
.
Mit dieser Näherung
wird die Kreisfläche mit einem relativen
Fehler von weniger als 5 % bestimmt.
Auszählen in einem Raster
Die Kreisfläche lässt sich annähernd bestimmen, indem man ihr viele kleine Quadrate unterlegt (z.B. mit Millimeterpapier). Zählt man alle Quadrate, die vollständig innerhalb des Kreises liegen, so erhält man einen etwas zu niedrigen Wert für die Fläche, zählt man auch alle Quadrate mit, die den Kreis lediglich schneiden, so ist der Wert zu groß. Der Mittelwert beider Ergebnisse ergibt eine Näherung für den Flächeninhalt des Kreises, deren Güte mit der Feinheit des Quadratrasters steigt.

Annäherung durch Integration
Man kann die Fläche des Kreises aus im Verhältnis zum Radius sehr schmalen Streifen zusammensetzen. Dazu verwendet man die Gleichungen
und
.
Annäherung durch Vielecke
Bei einer anderen Möglichkeit zur Kreisflächenbestimmung ist in den Kreis ein regelmäßiges Sechseck einzuzeichnen, dessen Ecken auf dem Kreis liegen. Werden nun die Seitenmitten vom Mittelpunkt aus auf den Kreis projiziert und diese neuen Punkte mit den alten Ecken verbunden, so entsteht ein regelmäßiges Zwölfeck. Wird dieser Vorgang wiederholt, entstehen nacheinander ein 24-Eck, ein 48-Eck und so fort.
In jedem Sechseck sind die Seiten gleich lang wie der Umkreisradius. Die Seiten der folgenden Vielecke ergeben sich mit Hilfe des Satzes von Pythagoras jeweils aus den Seiten der vorhergehenden. Aus den Seiten lassen sich die Flächen der Vielecke durch Dreiecksflächenberechnung exakt bestimmen. Sie sind alle etwas kleiner als die Kreisfläche, der sie sich bei steigender Eckenzahl jedoch annähern.
Entsprechend kann man mit einem Sechseck verfahren, das von außen an den Kreis gezeichnet ist, dessen Seitenmitten also auf ihm liegen. Man erhält eine fallende Folge von Flächenmaßen, deren Grenzwert wiederum die Kreisfläche ist.
Geometrische Sätze und Begriffe rund um den Kreis
Symmetrie und Abbildungseigenschaften
Der Kreis ist eine geometrische Figur von sehr hoher Symmetrie. Jede
Gerade durch seinen Mittelpunkt ist eine Symmetrieachse.
Zudem ist der Kreis rotationssymmetrisch,
d.h., jede Drehung um den Mittelpunkt
bildet den Kreis auf sich selbst ab. In der Gruppentheorie
werden die genannten Symmetrieeigenschaften des Kreises durch seine Symmetriegruppe
charakterisiert. Formal ergibt sich dafür die orthogonale Gruppe
,
das ist die Gruppe
der orthogonalen
-Matrizen.
Alle Kreise mit dem gleichen Radius sind zueinander kongruent, lassen sich also durch Parallelverschiebungen aufeinander abbilden. Zwei beliebige Kreise sind zueinander ähnlich. Sie lassen sich stets durch eine zentrische Streckung und eine Parallelverschiebung aufeinander abbilden.
Kreiswinkel und Winkelsätze


Eine Kreissehne mit Endpunkten A und B teilt einen gegebenen Kreis in zwei
Kreisbögen. Ein Winkel
mit Scheitel C auf einem der Kreisbögen wird Umfangswinkel oder
Peripheriewinkel genannt. Der Winkel
mit Scheitel im Mittelpunkt M heißt Mittelpunktswinkel oder
Zentriwinkel.
Im Spezialfall, dass die Sehne den Mittelpunkt enthält, also ein Durchmesser des Kreises ist, ist der Mittelpunktswinkel ein gestreckter Winkel mit 180°. In dieser Situation gilt eine grundlegende Aussage der Kreisgeometrie, der Satz von Thales: Er besagt, dass Umfangswinkel über einem Durchmesser stets rechte Winkel sind, also 90° betragen. Der Kreis um das rechtwinklige Dreieck wird in dieser Situation auch Thaleskreis genannt.
Auch im Fall einer beliebigen Kreissehne sind alle Umfangswinkel, die auf dem gleichen Kreisbogen liegen, gleich groß. Diese Aussage wird auch Umfangswinkelsatz genannt. Der Kreisbogen, auf dem die Scheitel der Umfangswinkel liegen, heißt Fasskreisbogen. Liegen Umfangswinkel und Zentriwinkel auf der gleichen Seite der Sehne, dann ist der Zentriwinkel doppelt so groß wie der Umfangswinkel (Kreiswinkelsatz). Zwei Umfangswinkel, die auf gegenüberliegenden Seiten der Sehne liegen, ergänzen einander zu 180°.
Der Umfangswinkel ist genauso groß wie der spitze Sehnentangentenwinkel zwischen der Sehne und der durch einen ihrer Endpunkte verlaufenden Tangente (Sehnentangentenwinkelsatz).
Sätze über Sehnen, Sekanten und Tangenten
Für Kreise gilt der Sehnensatz, der besagt: Schneiden zwei Sehnen [AC] und [BD] einander in einem Punkt S, so gilt
d.h., die Produkte der jeweiligen Sehnenabschnitte sind gleich.
Zwei Sehnen eines Kreises, die einander nicht schneiden, können verlängert werden zu Sekanten, die entweder parallel sind oder einander in einem Punkt S außerhalb des Kreises schneiden. Ist Letzteres der Fall, so gilt analog zum Sehnensatz der Sekantensatz
Im Fall einer Sekante, die den Kreis in den Punkte A und C schneidet, und einer Tangente, die den Kreis im Punkt B berührt, gilt der Sekanten-Tangenten-Satz: Ist S der Schnittpunkt von Sekante und Tangente, so folgt
Umkreise und Inkreise
Sind A, B, C drei Punkte, die nicht auf einer Geraden liegen, also ein nicht ausgeartetes Dreieck bilden, dann existiert ein eindeutig bestimmter Kreis durch diese Punkte, nämlich der Umkreis des Dreiecks ABC. Der Mittelpunkt des Umkreises ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Ebenso kann jedem Dreieck ein eindeutig bestimmter Kreis einbeschrieben werden, der die drei Seiten berührt, d.h., die Dreiecksseiten bilden Tangenten des Kreises. Dieser Kreis wird Inkreis des Dreiecks genannt. Sein Mittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden.
In der Elementargeometrie werden noch weitere Kreise am Dreieck betrachtet: Die Ankreise liegen außerhalb des Dreiecks und berühren eine Seite und die Verlängerungen der beiden anderen Seiten. Ein weiterer interessanter Kreis am Dreieck ist der Feuerbachkreis, benannt nach Karl Wilhelm Feuerbach. Auf ihm liegen die drei Seitenmittelpunkte und die drei Fußpunkte der Höhen. Da auf ihm außerdem die drei Mittelpunkte der Strecken zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks liegen, wird der Feuerbachkreis auch Neunpunktekreis genannt. Sein Mittelpunkt liegt wie der Schwerpunkt, der Umkreismittelpunkt und der Höhenschnittpunkt auf der eulerschen Geraden.
Im Gegensatz zu Dreiecken besitzen unregelmäßige Polygone (Vielecke) mit mehr als drei Ecken im Allgemeinen keinen Umkreis oder Inkreis. Für regelmäßige Polygone existieren beide, eingezeichnet oder nicht, allerdings stets. Ein Viereck, das einen Umkreis besitzt, wird Sehnenviereck genannt. Ein konvexes Viereck ist genau dann ein Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen. Ein Viereck, das einen Inkreis besitzt, wird Tangentenviereck genannt. Ein konvexes Viereck ist genau dann ein Tangentenviereck, wenn die Summe der Seitenlängen zweier gegenüberliegender Seiten gleich der Summe der beiden anderen Seitenlängen ist.
Kreisspiegelungen und Möbiustransformationen
Die Kreisspiegelung, auch Inversion genannt, ist eine spezielle Abbildung der
ebenen Geometrie, die eine „Spiegelung“ der euklidischen Ebene an einem
gegebenen Kreis
mit Mittelpunkt
und Radius
beschreibt. Ist
ein gegebener Punkt, dann ist sein Bildpunkt
dadurch bestimmt, dass er auf der Halbgeraden
liegt und sein Abstand von
die Gleichung
erfüllt. Die Kreisspiegelung bildet das Innere des gegebenen Kreises
auf sein Äußeres ab und umgekehrt. Alle Kreispunkte von
werden auf sich selbst abgebildet. Kreisspiegelungen sind winkeltreu, orientierungsumkehrend
und kreistreu. Letzteres bedeutet, dass verallgemeinerte Kreise – das sind
Kreise und Geraden – wieder auf verallgemeinerte Kreise abgebildet werden.
Die Hintereinanderausführung zweier Kreisspiegelungen ergibt eine Möbiustransformation. Möbiustransformationen – eine weitere wichtige Klasse von Abbildungen der Ebene – sind daher ebenfalls winkeltreu und kreistreu, allerdings orientierungserhaltend.
Kreisspiegelungen und Möbiustransformationen lassen sich besonders
übersichtlich mit Hilfe komplexer Zahlen darstellen: Bei einer Kreisspiegelung
eines Punktes
an dem Kreis
lautet die Formel für den Bildpunkt
Für die Spiegelung am Einheitskreis gilt einfach .
Möbiustransformationen der komplexen Ebene werden durch gebrochen lineare Funktionen der Gestalt
mit
und
dargestellt.
Konstruktionen mit Zirkel und Lineal

Ein klassisches Problem der Geometrie ist die Konstruktion geometrischer Objekte mit Zirkel und Lineal in endlich vielen Konstruktionsschritten aus einer gegebenen Punktemenge. In jedem Schritt dürfen dabei Geraden durch gegebene oder bereits konstruierte Punkte gezogen werden sowie Kreise um solche Punkte mit gegebenem oder bereits konstruiertem Radius gezogen werden. Die dadurch konstruierten Punkte ergeben sich als Schnittpunkte zweier Geraden, zweier Kreise oder einer Geraden mit einem Kreis. Naturgemäß spielen daher bei allen Konstruktionen mit Zirkel und Lineal Kreise eine wichtige Rolle.
Im Folgenden sollen exemplarisch einige Konstruktionen angesprochen werden, die im Zusammenhang mit der Geometrie von Kreisen von Bedeutung sind.
Thaleskreis

Tangenten mit Hilfe des Thaleskreises durch Punkt
Für die Konstruktion des Thaleskreises über einer gegebenen Strecke
wird zunächst der Mittelpunkt
dieser Strecke konstruiert, der auch der Mittelpunkt des Thaleskreises ist. Dazu
werden um
und
jeweils zwei kurze Kreisbögen mit dem gleichen Radius
geschlagen, wobei
so groß gewählt werden muss, dass die vier Kreisbögen sich in zwei Punkten
und
schneiden. Das ist z.B. für
der Fall. Die Strecke
schneidet dann
im Mittelpunkt
.
Der gesuchte Thaleskreis ist nun der Kreis mit Mittelpunkt
und Radius
.
Konstruktion von Tangenten
Gegeben sei ein Punkt
außerhalb eines Kreises
mit Mittelpunkt
und es sollen die beiden Tangenten an den Kreis konstruiert werden, die durch
den Punkt
laufen. Diese elementare Konstruktionsaufgabe lässt sich einfach mit Hilfe des
Satzes von Thales lösen: Man konstruiert den Thaleskreis mit der Strecke
als Durchmesser. Die Schnittpunkte dieses Kreises mit
sind dann die Berührpunkte der gesuchten Tangenten.
Flächenverdoppelung

Die Fläche eines Kreises lässt sich geometrisch verdoppeln, indem ein Quadrat gezeichnet wird, dessen eine Ecke im Kreismittelpunkt liegt, wobei zwei weitere Ecken auf dem Kreisbogen liegen. Durch die vierte Ecke wird ein Kreis um den alten Mittelpunkt gezogen. Dieses Verfahren wurde im 13. Jahrhundert im Bauhüttenbuch des Villard de Honnecourt dargestellt. Dieses Verfahren funktioniert, da (nach dem Satz des Pythagoras)
und damit der Flächeninhalt des großen Kreises
genau doppelt so groß ist wie der des kleinen Kreises.
Kreisteilung
Ein weiteres bereits in der Antike untersuchtes Konstruktionsproblem ist die
Kreisteilung. Hierbei soll zu einer gegebenen natürlichen
Zahl
einem gegebenen Kreis ein regelmäßiges
-Eck
einbeschrieben werden. Die auf dem Kreis gelegenen Eckpunkte teilen diesen dann
in
gleich lange Kreisbögen. Diese Konstruktion ist nicht für alle
möglich: Mit Hilfe der algebraischen
Theorie der Körpererweiterungen
lässt sich zeigen, dass sie genau dann durchführbar ist, wenn
eine Primfaktorzerlegung
der Form
hat mit
und paarweise verschiedenen fermatschen
Primzahlen
,
also Primzahlen der Form
.
Damit ist die Konstruktion also beispielsweise für
möglich, jedoch nicht für z.B.
.
Carl
Friedrich Gauß wies im Jahre 1796 nach, dass die Konstruktion des
regelmäßigen Siebzehnecks
unter alleiniger Verwendung von Zirkel und Lineal
möglich ist.
Kreisberechnung in der Analysis
In der modernen Analysis
werden die trigonometrischen
Funktionen und die Kreiszahl
üblicherweise zunächst ohne Rückgriff auf die elementargeometrische Anschauung
und auf spezielle Eigenschaften des Kreises definiert. So lassen sich etwa Sinus und Kosinus
über ihre Darstellung als Potenzreihe
definieren. Eine gängige Definition für den Wert von
ist dann das Doppelte der kleinsten positiven Nullstelle des Kosinus.
Der Kreis als Kurve
In der Differentialgeometrie,
einem Teilgebiet der Analysis, das geometrische Formen mit Hilfe der Differential- und
Integralrechnung
untersucht, werden Kreise als spezielle Kurven
angesehen. Diese Kurven lassen sich mit Hilfe der oben genannten Parameterdarstellung
als Weg
beschreiben. Legt man den Koordinatenursprung in den Mittelpunkt eines Kreises
mit Radius ,
dann ist durch die Funktion
mit
eine solche Parametrisierung gegeben. Mit Hilfe der trigonometrischen Formel
folgt für die euklidische
Norm der parametrisierten Punkte
,
das heißt, sie liegen tatsächlich auf einem Kreis mit Radius
.
Da Sinus und Kosinus
-periodische
Funktionen sind, entspricht das Definitionsintervall
von
genau einem Kreisumlauf.
Kreisumfang
Der Umfang des Kreises ergibt sich als Länge
des Weges
durch Integration
zu
Analog gilt für die Länge
des durch
gegebenen Teilkreisbogens
.
Dadurch erhält man als Parametrisierung des Kreises nach der Bogenlänge
mit .
Flächeninhalt
Der Flächeninhalt
der Kreisscheibe
,
also das Maß
der Menge
,
kann als (zweidimensionales) Integral
dargestellt werden. Um die etwas mühsame Berechnung dieses Integrals in
kartesischen Koordinaten zu umgehen, ist es günstig, eine Transformation
,
auf Polarkoordinaten
durchzuführen. Damit ergibt sich
Eine andere Möglichkeit zur Berechnung der Kreisfläche besteht darin,
die Sektorformel
von Leibniz auf die Parameterdarstellung des Kreisrandes anzuwenden. Mit
,
erhält man damit ebenfalls
Krümmung
Für die oben hergeleitete Parametrisierung
des Kreises nach seiner Bogenlänge ergibt sich
Für die Krümmung des Kreises erhält man daher
Die Krümmung des Kreises ist also konstant und der Krümmungsradius
ist gerade sein Radius.
In der Differentialgeometrie wird gezeigt, dass eine ebene Kurve bis auf Kongruenz durch ihre Krümmung eindeutig bestimmt ist. Die einzigen ebenen Kurven mit konstanter positiver Krümmung sind daher Kreisbögen. Im Grenzfall, dass die Krümmung konstant gleich 0 ist, ergeben sich Geradenstücke.
Isoperimetrisches Problem
Unter allen Flächen der euklidischen Ebene mit gegebenem Umfang besitzt die Kreisfläche den größten Flächeninhalt. Umgekehrt hat die Kreisfläche bei gegebenem Flächeninhalt den kleinsten Umfang. In der Ebene ist der Kreis daher die eindeutig bestimmte Lösung des sog. isoperimetrischen Problems. Obwohl diese anschaulich einleuchtende Tatsache schon den Mathematikern im antiken Griechenland bekannt war, wurden formale Beweise erst im 19. Jahrhundert erbracht. Da eine Kurve gesucht ist, die ein Funktional maximiert, nämlich den umschlossenen Flächeninhalt, handelt es sich dabei aus moderner Sicht um ein Problem der Variationsrechnung. Ein gängiger Beweis für stückweise stetige Kurven verwendet die Theorie der Fourierreihen.
Verallgemeinerungen und verwandte Themen
Sphäre
Es ist möglich, den Kreis als Objekt der Ebene in den dreidimensionalen Raum
zu verallgemeinern. Dann erhält man die Hülle einer Kugel.
Dieses Objekt wird in der Mathematik Sphäre oder genauer 2-Sphäre genannt.
Analog lässt sich die 2-Sphäre auf
Dimensionen zur
-Sphäre
verallgemeinern. In diesem Kontext nennt man den Kreis auch 1-Sphäre.
Kegelschnitte

In der ebenen Geometrie kann der Kreis als spezielle Ellipse aufgefasst werden, bei der die beiden Brennpunkte mit dem Kreismittelpunkt zusammenfallen. Beide Halbachsen sind dabei gleich dem Kreisradius. Der Kreis ist daher ein spezieller Kegelschnitt: Er entsteht als Schnitt eines geraden Kreiskegels mit einer Ebene senkrecht zu Kegelachse. Er ist damit ein Spezialfall einer zweidimensionalen Quadrik.
Hierbei ergibt sich eine weitere, äquivalente Definition für Kreise
(Kreis
des Apollonios): Ein Kreis ist die Menge aller Punkte in der Ebene, für die
der Quotient
ihrer Abstände von zwei gegebenen Punkten konstant ist. Die beiden Punkte liegen
auf einem von
ausgehenden Strahl
im Abstand
bzw.
und wechselseitig auf der Polaren
des jeweils anderen Punktes als Pol. Ähnliche Definitionen gibt es auch für die
Ellipse (konstante Summe), Hyperbel
(konstante Differenz) und die Cassinische
Kurve (konstantes Produkt der Abstände).
Kreise in der synthetischen Geometrie
In der synthetischen
Geometrie können Kreise in bestimmten affinen
Ebenen (zum Beispiel präeuklidischen
Ebenen) ohne einen Abstandsbegriff allein durch eine
Orthogonalitätsrelation definiert werden, indem der Satz vom Umkreis (Mittellotensatz) zur
Definition des Kreises verwendet wird. Dadurch kann dann ein schwächerer Begriff
der „Abstands-“ oder „Längengleichheit“ von Punktepaaren
in solchen Ebenen eingeführt werden. → Siehe dazu Präeuklidische
Ebene.
Siehe auch
- Einheitskreis
- Großkreis
- Kleinkreis
- Kreisbogen
- Kreisgruppe
- Kreisring
- Kreissegment
- Kreissektor
- Kreiswinkel
- Sehne (Geometrie)
Literatur
- Ilka Agricola, Thomas Friedrich: Elementargeometrie. 3. Auflage. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-1385-5.
- Christian Bär: Elementare Differentialgeometrie. 2. Auflage. Walter de Gruyter, Berlin 2010, ISBN 978-3-11-022458-0.
- Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Eine aufgabenorientierte Einführung. Vieweg+Teubner, Wiesbaden 2009, ISBN 978-3-8348-0856-1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.04. 2023



