Funktion (Mathematik)
In der Mathematik ist eine
Funktion (lateinisch
functio) oder
Abbildung eine Beziehung (Relation)
zwischen zwei Mengen,
die jedem Element der einen Menge (Funktionsargument, unabhängige Variable,
-Wert)
genau ein Element der anderen Menge (Funktionswert, abhängige Variable,
-Wert)
zuordnet. Der Funktionsbegriff wird in der Literatur unterschiedlich definiert,
jedoch geht man generell von der Vorstellung aus, dass Funktionen mathematischen
Objekten mathematische Objekte zuordnen, zum Beispiel jeder reellen Zahl
deren Quadrat. Das Konzept der Funktion oder Abbildung nimmt in der modernen
Mathematik eine zentrale Stellung ein; es enthält als Spezialfälle unter anderem
parametrische
Kurven, Skalar- und Vektorfelder,
Transformationen,
Operationen,
Operatoren
und vieles mehr.
Begriffsgeschichte
Erste Ansätze zu einer impliziten Verwendung des Funktionsbegriffs in
Tabellenform (Schattenlänge abhängig von der Tageszeit, Sehnenlängen abhängig
vom Zentriwinkel etc.) sind bereits in der Antike zu erkennen. Den ersten Beleg
einer expliziten Definition des Funktionsbegriffs findet man bei Nikolaus von Oresme,
der im 14. Jahrhundert Abhängigkeiten sich ändernder Größen (Wärme,
Bewegung etc.) graphisch durch senkrecht aufeinander stehende Strecken
(longitudo, latitudo) darstellte.
Am Beginn des Prozesses zur Entwicklung des Funktionsbegriffs stehen Descartes und
Fermat, die mit Hilfe
der von François Viète
eingeführten Variablen
die analytische Methode der Einführung von Funktionen entwickelten.
Funktionale Abhängigkeiten sollten durch Gleichungen wie zum Beispiel
dargestellt werden. In der Schulmathematik wurde dieser naive Funktionsbegriff
bis weit in die zweite Hälfte des 20. Jahrhunderts beibehalten. Die erste
Umschreibung des Funktionsbegriffs nach dieser Idee stammt von James Gregory in
seinem 1667 erschienenen Buch Vera circuli et hyperbolae quadratura. Der
Begriff Funktion kommt wohl erstmals 1673 in einem Manuskript von Leibniz
auf, der in seiner Abhandlung von 1692 De linea ex lineis numero infinitis
ordinatim ductis auch die Begriffe „Konstante“, „Variable“, „Ordinate“ und
„Abszisse“ benutzt. Im Schriftwechsel zwischen Leibniz und Johann I Bernoulli
wird der Funktionsbegriff von der Geometrie losgelöst und in die Algebra
übertragen. In Beiträgen von 1706, 1708 und 1718 stellt Bernoulli diese
Entwicklung dar. 1748 präzisiert Leonhard
Euler, ein Schüler Johann Bernoullis, in seinem Buch Introductio in
analysin infinitorum den Funktionsbegriff weiter.
Bei Euler findet man zwei verschiedene Erklärungen des Funktionsbegriffs: Zum
einen stellt jeder „analytische Ausdruck“ in
eine Funktion dar, zum anderen wird
im Koordinatensystem durch eine freihändig gezeichnete Kurve definiert.
1755 formuliert er diese Vorstellungen ohne Verwendung des Terminus
„analytischer Ausdruck“ um. Außerdem führte er bereits 1734 die Schreibweise
ein. Er unterscheidet zwischen eindeutigen und mehrdeutigen Funktionen. Bei
Euler ist damit auch die Umkehrung der Normalparabel,
bei der jeder nicht-negativen reellen Zahl sowohl ihre positive als auch ihre
negative Wurzel zugeordnet wird, als Funktion zugelassen. Für Lagrange sind nur
Funktionen zulässig, die durch Potenzreihen definiert sind, wie er 1797 in
seiner Théorie des fonctions analytiques festlegt. Eine fruchtbare
Auseinandersetzung über das Bewegungsgesetz einer schwingenden Saite, zu dem d’Alembert
1747, Euler 1748 und Daniel Bernoulli 1753 unterschiedliche Lösungen
vorstellten, führte zur Entdeckung der Definitionsmenge
und einem weiter präzisierten Funktionsbegriff, in dem schon so etwas wie
eindeutige Zuordnung umschrieben wird, durch Fourier
in seinem 1822 erschienenen Buch Théorie analytique de la chaleur.
Ähnliches formuliert Cauchy
1823 in Résumé des leçons … sur le calcul infinitésimal.
Als die Analysis im 19. Jahrhundert
mit einem exakten Grenzwertbegriff
auf eine neue Grundlage gestellt wurde, wurden Eigenschaften, die bisher als für
Funktionen konstituierend aufgefasst wurden, in einem Exaktifizierungsprozess
als selbständige Begriffe eingeführt und vom Funktionsbegriffs losgelöst. Dirichlet,
ein Schüler Fouriers, formulierte diese neue Sicht: „Ideen an die Stelle von
Rechnungen“ und stellte 1837 seine Ideen dar. Stokes führte in
Arbeiten 1848 und 1849 ähnliche Ansichten aus. So verfuhr Riemann, Schüler von
Dirichlet, 1851 in Grundlagen für eine allgemeine Theorie der Functionen
einer veränderlichen complexen Größe mit der Stetigkeit, später folgten
Integrierbarkeit und Differenzierbarkeit. Eine Zusammenfassung dieser
Entwicklung macht Hermann Hankel
1870 in Untersuchungen über die unendlich oft oscillierenden und unstetigen
Functionen. Auch hier wird noch nicht zwischen der Funktion
und dem Funktionswert
an der Stelle
unterschieden.
Weierstraß, Dedekind und andere entdeckten, dass Grenzwerte unendlicher Folgen „klassischer“ Funktionen sprunghaft sein können und sich nicht immer durch „geschlossene“ Formeln, d.h. mit endlich vielen Rechenoperationen, ausdrücken lassen. Das erzwang eine schrittweise Ausweitung des Funktionsbegriffs.
Davon unabhängig wurde im 19. Jahrhundert die Gruppentheorie begründet, mit der man systematisch untersuchen kann, wie sich algebraische Gleichungen unter der Wirkung aufeinanderfolgender Transformationen verändern. Bei der Anwendung dieser Theorie auf geometrische Probleme wurden gleichbedeutend mit Transformation auch die Begriffe Bewegung und Abbildung gebraucht.
Als Anfang des 20. Jahrhunderts die Grundlagen der Mathematik einheitlich in
der Sprache der Mengenlehre
formuliert wurden, stellten sich die mathematischen Begriffe Funktion und
Abbildung als deckungsgleich heraus. Im Sprachgebrauch wirken die
unterschiedlichen Traditionen jedoch fort. In der Analysis spricht man heute
häufig noch von Funktionen, während man in der Algebra und in der Geometrie von
Abbildungen spricht. Einige Mathematiker unterscheiden auch heute noch streng
zwischen einer Abbildung und einer Funktion. Diese verstehen unter einer
Funktion eine Abbildung in den reellen oder komplexen Zahlenkörper (
bzw.
)
oder auch Potenzen
davon (
bzw.
),
andererseits ist es in der Booleschen
Algebra gebräuchlich, von Booleschen
Funktionen zu sprechen.
Weitere Synonyme für Funktion in spezielleren Zusammenhängen sind unter anderem Operator in der Analysis, Operation, Verknüpfung und (etwas verallgemeinert) Morphismus in der Algebra.
Heute sehen manche Autoren den Funktionsbegriff (genauso wie den Relationsbegriff) nicht unbedingt als auf Mengen beschränkt an, sondern lassen jede aus geordneten Paaren bestehende Klasse, die keine verschiedenen Elemente mit gleicher linker Komponente enthält, als Funktion gelten. Mengentheoretisch ausgedrückt werden Funktionen also als rechtseindeutige Relationen definiert.
Definition
Grundidee
Eine Funktion
ordnet jedem Element
einer Definitionsmenge
genau ein Element
einer Zielmenge
zu.
Schreibweise:
, oder auch äquivalent:
Für das dem Element
zugeordnete Element der Zielmenge schreibt man im Allgemeinen
.
Anmerkungen:
- Die Umkehrung gilt nicht: Ein Element der Zielmenge kann genau einem,
mehreren, aber auch keinem Element der Definitionsmenge zugeordnet
sein.
Beispiel: Die Betragsfunktionordnet die Zahlen +1 und −1 der Definitionsmenge der Zahl +1 der Zielmenge zu. Der Zahl −1 der Zielmenge ist keine Zahl der Definitionsmenge zugeordnet.
- Oft ist an Stelle der Definitionsmenge zunächst eine Quellmenge
gegeben. Wenn
als Rechenvorschrift gegeben ist, erhält man die Definitionsmenge
, indem man von
diejenigen Elemente ausschließt, für die
nicht definiert ist. Siehe auch Abschnitt „Partielle Funktionen“.
Mengentheoretische Definition
Mengentheoretisch ist eine Funktion eine spezielle Relation:
- Eine Funktion von der Menge
in die Menge
ist eine Menge
, die die folgenden Eigenschaften hat:
ist eine Teilmenge des kartesischen Produkts
von
und
, d.h.
ist eine Relation zwischen
und
.
- Für jedes Element
aus
existiert mindestens ein Element
in
, so dass das geordnete Paar
Element der Relation
ist.
ist also linkstotal.
- Zu jedem Element
von
gibt es höchstens ein Element
von
, so dass das Paar
in
liegt.
ist damit rechtseindeutig oder funktional.
Die letzten beiden Eigenschaften lassen sich auch wie folgt zusammenfassen:
-
- Zu jedem Element
von
gibt es genau ein Element
von
, so dass das Paar
Element der Relation
ist.
- Zu jedem Element
Oft möchte man aber auch die Zielmenge explizit zu einem Teil der Funktion machen, zum Beispiel um Aussagen zur Surjektivität (als eine Eigenschaft der betrachten Funktion selbst) anstellen zu können:
- Ein Paar
, bestehend aus einer Menge
und einer Menge von Paaren
mit einer weiteren Menge
heißt Funktion von der Menge
nach
, wenn gilt: Zu jedem Element
von
gibt es genau ein Element
von
(geschrieben
), so dass das Paar
Element von
ist.
wird dann auch der Graph
der Funktion
genannt. Die Definitionsmenge
der Funktion ist dabei durch ihren Graphen eindeutig bestimmt und besteht aus
den ersten Komponenten aller Elemente des Graphen. Stimmen zwei Funktionen in
ihren Graphen überein, so sagt man auch, sie seien im Wesentlichen gleich.
Insbesondere ist jede Funktion
im Wesentlichen gleich mit der surjektiven Funktion
mit der Bildmenge
.
Oft empfiehlt es sich auch noch die Definitionsmenge hinzunehmen und eine
Funktion entsprechend als ein Tripel
zu definieren. Diese Definition stimmt dann überein mit der entsprechenden
ausführlichen Definition bei Relationen, so dass auch Multifunktionen
und partielle
Funktionen auf gleiche Weise erfasst sind.
Notation
Schreibweisen
Eine Zuordnung kann unter anderem in einer der folgenden Formen beschrieben werden:
- Funktionsgleichung mit Definitionsmenge
- Eindeutige Zuordnungsvorschrift (englisch: maplet) mit Definitionsmenge
- Eindeutige Zuordnungsvorschrift mit Definitions- und Zielmenge
, oder äquivalent:
- Familienschreibweise (mit der Bezeichnung Indexmenge für die Definitionsmenge)
[1]
- Wertetabelle (für endliche, aber auch abzählbar unendliche Definitionsmengen)
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | … |
- Als Relation insbesondere auch als aufgezählt oder beschrieben dargestellte Teilmenge
- Als Ergebnis von Verknüpfungen und Operationen (zum Beispiel Komposition, Differenzierung, Bildung der Umkehrfunktion, …), die auf andere Funktionen angewendet werden
Sprechweisen
Für die Zuordnung eines Funktionswertes
zu einem Argument
gibt es eine Reihe verschiedener Sprech- oder ausführlicher Schreibweisen, die
alle mehr oder weniger gleichwertig sind und vor allem in Abhängigkeit von dem,
was vordergründig ausgedrückt werden soll, vom jeweiligen Kontext, der benutzten
Symbolik und auch vom Geschmack des Sprechers (Schreibers) gewählt werden. Hier
einige Beispiele:
wird abgebildet auf
von
von
wird
eindeutig zugeordnet (vornehmlich, wenn das
-Symbol in der Symbolik steht)
gleich
von
(vornehmlich, wenn ein Gleichheitszeichen in der Symbolik steht)
ist das Bild von
unter der Abbildung
Davon zu unterscheiden ist die Sprech- und Schreibweise: „
ist eine Funktion von
“,
die vor allem in der Physik sehr nahestehenden Bereichen der Mathematik
auftaucht. Sie ist die ältere und ursprüngliche Sprech- und Schreibweise und
beschreibt die Abhängigkeit einer Variablen
von einer anderen Variablen
,
im Gegensatz dazu, dass mit Hilfe der Variablen
und
(stellvertretend) die Zuordnung bestimmter Elemente von Mengen beschrieben wird.
Die „physikalische“ Sprechweise stammt von dem Vorgehen, zunächst zwei
veränderlichen Größen (der physikalischen Realität) Symbole, nämlich die
Variablen
und
,
zuzuordnen und danach deren Abhängigkeit festzustellen. Steht
beispielsweise
für die Raumtemperatur und
für die Zeit, so wird man feststellen können, dass sich die Raumtemperatur in
Abhängigkeit von der Zeit ändert und somit „die Raumtemperatur eine Funktion
der Zeit ist“ oder stellvertretend „
eine Funktion von
ist.“
Statt Definitionsmenge
wird auch Definitionsbereich, Urbildmenge oder schlicht Urbild
gesagt. Die Elemente von
heißen Funktionsargumente, Funktionsstellen oder Urbilder, salopp
auch
-Werte.
Die Zielmenge
wird auch Wertemenge oder Wertebereich genannt, die Elemente von
heißen Zielwerte oder Zielelemente, salopp auch
-Werte.
Diejenigen Elemente von
,
die tatsächlich auch als Bild eines Arguments auftreten, heißen
Funktionswerte, Bildelemente oder schlicht Bilder.
Darstellung
Eine Funktion ,
kann man visualisieren, indem man ihren Graphen in ein (zweidimensionales) Koordinatensystem
zeichnet. Der Funktionsgraph
einer Funktion
kann mathematisch definiert werden als die Menge aller Elementepaare
,
für die
ist. Der Graph einer stetigen
Funktion auf einem zusammenhängenden Intervall bildet eine zusammenhängende
Kurve
(genauer: die Menge der Punkte der Kurve, aufgefasst als Unterraum des topologischen Raumes
ist zusammenhängend).
Analog kann man Funktionen ,
und
,
visualisieren, indem man sie in ein dreidimensionales Koordinatensystem
zeichnet. Ist
stetig, so ergibt sich eine Kurve (die auch Ecken haben kann), die sich durch
das Koordinatensystem „schlängelt“. Ist
stetig, so ergibt sich eine Fläche als Bild, typischerweise in Form einer
„Gebirgslandschaft“.
Computerprogramme zur Darstellung von Funktionen heißen Funktionenplotter. Funktionsprogramme gehören auch zum Funktionsumfang von Computeralgebrasystemen (CAS), matrizenfähigen Programmierumgebungen wie MATLAB, Scilab, GNU Octave und anderen Systemen. Die wesentlichen Fähigkeiten eines Funktionenplotters sind auch auf einem graphikfähigen Taschenrechner verfügbar. Es gibt auch Web-gestützte Angebote, die nur einen aktuellen Browser benötigen.
- Beispiele einiger Funktionsgraphen
-
 Lineare Funktion (genauer: Affine Abbildung)
Lineare Funktion (genauer: Affine Abbildung) -
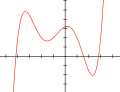 Polynomfunktion 5. Grades
Polynomfunktion 5. Grades -
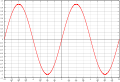
 Realteil der komplexen Exponentialfunktion
Realteil der komplexen Exponentialfunktion
Grundeigenschaften
Bild und Urbild
Das Bild eines Elements
der Definitionsmenge ist einfach der Funktionswert
.
Das Bild einer Funktion ist die Menge der Bilder aller Elemente der
Definitionsmenge
,
also
.
Das Bild einer Funktion ist folglich eine Teilmenge der Zielmenge und wird
Bildmenge genannt. Ist allgemeiner
eine Teilmenge von
,
dann ist
das Bild von
unter der Funktion
.
Das Urbild eines Elements
der Zielmenge
ist die Menge aller Elemente der Definitionsmenge, deren Bild
ist. Es ist
,
(
ist im Allgemeinen keine eindeutige Funktion ist, sondern eine Multifunktion,
zu Schreibweise
siehe dort, sowie bei Relation
#Relationen und Funktionen und Korrespondenz
(Mathematik)).
Oft werden diese Fasern
einfach mit
bezeichnet, was aber im Fall (eindeutig) umkehrbarer Funktionen einerseits
x, andererseits {x} bezeichnet.
Das Urbild einer Teilmenge
der Zielmenge ist die Menge aller Elemente der Definitionsmenge, deren Bild
Element dieser Teilmenge ist:
.
Injektivität, Surjektivität, Bijektivität
- Eine Funktion ist injektiv,
wenn jedes Element der Zielmenge
höchstens ein Urbild hat. D.h., aus
folgt
- Sie ist surjektiv,
wenn jedes Element der Zielmenge
mindestens ein Urbild hat. D.h., zu beliebigem
gibt es ein
, sodass
- Sie ist bijektiv, wenn sie injektiv und surjektiv ist, wenn also jedes Element der Zielmenge genau ein Urbild hat.
Stelligkeit
Eine Funktion ,
deren Definitionsmenge
eine Produktmenge
ist, heißt oft zweistellig.
Den Wert von
,
der bei Anwendung von
auf das Paar
erhalten wird, bezeichnet man mit
.
Analoges gilt für höhere Stelligkeiten. Eine Funktion
bezeichnet man üblicherweise als dreistellig. Eine Funktion, deren
Definitionsmenge keine Produktmenge ist (oder bei der die innere Struktur der
Definitionsmenge keine Rolle spielt) bezeichnet man als einstellig. Unter
einer nullstelligen Funktion versteht man eine Funktion, deren Definitionsmenge
das leere
Produkt
ist, bei einem beliebigen Funktionswert. Daher können nullstellige Funktionen
als Konstanten
aufgefasst werden, was bei algebraischen
Strukturen (wie auch bei heterogenen
Algebren) Anwendung findet.
Statt nullstellig, einstellig, zweistellig, dreistellig sagt man auch oft unär, binär, ternär; Stelligkeit wird daher auch als „Arität“ (englisch: arity) bezeichnet.
Menge der Funktionen
Mit [2]
oder
wird die Menge aller Abbildungen von
nach
bezeichnet:
Für die Mächtigkeit gilt:
Operationen
Einschränkung
Die Einschränkung einer Funktion
auf eine Teilmenge
der Definitionsmenge
ist die Funktion
,
deren Graph durch
gegeben ist.
Umkehrfunktion
Zu jeder bijektiven Funktion
gibt es eine Umkehrfunktion
,
sodass
das eindeutig bestimmte Element
ist, für das
gilt. Die Umkehrfunktion erfüllt damit für alle
.
Bijektive Funktionen werden daher auch als eindeutig umkehrbare Funktionen bezeichnet.
Verkettung
Zwei Funktionen
und
,
bei denen der Wertebereich der ersten Funktion mit dem Definitionsbereich der
zweiten Funktion übereinstimmt (oder als Teilmenge enthalten ist), können
verkettet werden. Die Verkettung oder Hintereinanderausführung dieser beiden
Funktionen ist dann eine neue Funktion, die durch
gegeben ist. In dieser Notation steht meist die zuerst angewandte Abbildung
rechts, das heißt bei
wird zuerst die Funktion
angewandt und dann die Funktion
.
Gelegentlich wird in der Literatur allerdings auch die umgekehrte Reihung
verwendet und
geschrieben.
Verknüpfung

Ist auf der Zielmenge
eine innere
zweistellige Verknüpfung
gegeben, so lässt sich auch für Funktionen
eine innere zweistellige Verknüpfung definieren:
.
Beispiele hierfür sind die punktweise Addition und Multiplikation von
Funktionen. Weiter lässt sich mit Hilfe einer äußeren
zweistelligen Verknüpfung der Form
auch die Verknüpfung einer Funktion mit einem Element aus
definieren:
Beispiel hierfür ist die punktweise Multiplikation einer Funktion mit einem
Skalar.
Analog lässt sich so auch eine äußere Verknüpfung der Form
definieren. Sind Verknüpfungen der gleichen Art sowohl auf der Definitionsmenge,
als auch auf der Zielmenge gegeben, dann heißt eine Funktion verträglich
mit diesen Verknüpfungen, wenn sich die Bilder bezüglich der einen Verknüpfung
genauso verhalten wie die Urbilder bezüglich der anderen Verknüpfung.
Weitere Eigenschaften
Algebraische Eigenschaften
- Eine Funktion ist idempotent,
wenn
ist, d.h.
für alle Elemente
der Definitionsmenge gilt.
- Sie ist eine Involution,
wenn
ist, also
für alle Elemente
der Definitionsmenge gilt und für mindestens ein
der Definitionsmenge
ist.
- Ein Fixpunkt
ist ein Element
der Definitionsmenge von
, für das
gilt.
- Identität
- Konstanz
Analytische Eigenschaften
- Beschränktheit
- Periodizität
- Monotonie
- Symmetrie
- Stetigkeit
- Differenzierbarkeit
- Glattheit
- Holomorphie
- Homogenität
- Messbarkeit
- Integrierbarkeit
- Konvexität
Spezielle Funktionen
- Reellwertige Funktion, die sich dadurch auszeichnet, dass ihre Zielmenge innerhalb der reellen Zahlen liegt
- Komplexwertige Funktion, die sich dadurch auszeichnet, dass ihre Zielmenge innerhalb der komplexen Zahlen liegt
- Homogene lineare
Funktion (auch: Proportionalität):
allgemein beschrieben durch
; ist ein Homomorphismus bezüglich der Addition
- Allgemeine lineare
Funktion (oder affine Funktion): allg. beschrieben durch
; siehe auch affine Abbildung
- Quadratische
Funktion: allg. beschrieben durch
(s. Quadratische Gleichung)
- Potenzfunktion
- Polynomfunktionen;
auch ganzrationale Funktion: allg. beschrieben durch
oder
- Rationale
Funktion; gebrochen-rationale Funktion: Quotient zweier
Polynom-Funktionen,
- Wurzelfunktion: besteht aus gebrochenrationalen Funktionen, verknüpft durch die Grundrechenarten und Wurzelausdrücke
- Exponentialfunktion
- Logarithmus
- Trigonometrische Funktion: sin, cos, tan, cot, sec, csc
- Betragsfunktion
- Maximumsfunktion und Minimumsfunktion
- Gaußsche Ganzzahlfunktion
Verwendung
Ein fundamentales Konzept in der Mathematik stellen Strukturen dar, die dadurch entstehen, dass Mengen in Verbindung mit dazugehörigen Abbildungen gesehen werden. Derartige Strukturen bilden die Grundlage praktisch aller mathematischen Disziplinen, sobald sie über elementare Mengenlehre, kombinatorische Probleme oder grundlegende mathematisch-philosophische Fragestellungen hinausgehen.
Mengen können beispielsweise durch sogenannte Verknüpfungen
strukturiert werden. Der wichtigste Spezialfall ist die innere zweistellige
Verknüpfung, dabei handelt es sich um eine Abbildung der Form .
Beispiele für innere zweistellige Verknüpfungen sind Rechenoperationen, wie die
Addition oder Multiplikation auf Zahlenmengen. Dementsprechend wird das Bild
eines Paares
unter einer Verknüpfung
üblicherweise in der Form
geschrieben.
Weitere wichtige Beispiele solcher Strukturen sind algebraische, geometrische und topologische Strukturen, wie beispielsweise Skalarprodukte, Normen und Metriken.
Verallgemeinerungen
Multifunktionen
Eine Multifunktion
(auch mehrwertige Funktion oder Korrespondenz genannt) ist eine linkstotale
Relation. Das heißt, die Elemente der Definitionsmenge
können auf mehrere Elemente der Zielmenge
abgebildet werden. Man schreibt auch
.
Wenn
eine Menge ist, dann kann man jede Multifunktion
auch als eine Funktion
darstellen, die in die Potenzmenge von
geht:
. [3]
Im Fall
stellt eine mehrwertige Funktion
eine Transitionsrelation
dar, und
ist die zugehörige Transitionsfunktion.
Die Verkettung von Multifunktionen lässt sich genauso definieren wie für (eindeutige) Funktionen, mengentheoretisch ist dies äquivalent einer Verkettung zweier zweistelliger Relationen.
Umkehrungen von Funktionen als Multifunktionen
Ein Beispiel für Multifunktionen sind die Umkehrfunktionen (Umkehrungen) von
nicht injektiven Funktionen. Wenn
surjektiv ist, gilt automatisch:
ist eine Multifunktion. Die Darstellung der Umkehrfunktion in die Potenzmenge
von
liefert mit
die Fasern von
(siehe
oben).
Die Verkettung einer Funktion mit ihrer (allgemein nicht eindeutigen)
Umkehrung in der Form
ist eine Äquivalenzrelation,[4]
die durch
induzierte Äquivalenzrelation. Zwei Elemente aus dem Definitionsbereich
sind genau dann äquivalent, wenn sie denselben Funktionswert haben.
Partielle Funktionen
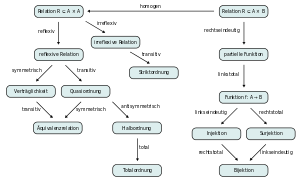
Wohl zu unterscheiden vom Begriff der Funktion ist der Begriff der partiellen Funktion,
man spricht auch von einer „nicht überall definierten Funktion“ oder „funktionalen
Relation“. Hier darf es Elemente der Quellmenge (-Werte)
geben, denen kein Wert der Zielmenge (
-Wert)
zugeordnet ist. Hier ist dann die Nennung der Quellmenge in der obigen
Tripelschreibweise tatsächlich notwendig. Allerdings darf es auch dort für einen
-Wert
nicht mehr als einen
-Wert
geben. Um partielle Funktionen von Funktionen zu unterscheiden, bezeichnet man
Letztere auch als totale oder überall definierte Funktionen.
Die Menge [2]
der partiellen Abbildungen von
nach
ist die Vereinigung der totalen Abbildungen von Teilmengen von
nach
:
Sind die Mengen endlich, so gilt für Ihre Kardinalzahlen
,
schließlich kann man jede partielle Abbildung auf D umkehrbar eindeutig zu
einer totalen Abbildung fortsetzen, indem man einen beliebigen festen
Funktionswert
festschreibt, der nicht in
enthalten ist; und diese Operation stellt eine bijektive Abbildung auf
dar.
Jede partielle Funktion
ist im Wesentlichen gleich mit der (totalen) Funktion
mit der Urbildmenge
.
Funktionen mit Werten in einer echten Klasse
Häufig liegen die Werte einer Funktion nicht in einer Zielmenge, sondern
lediglich in einer echten
Klasse, beispielsweise sind Mengenfolgen
„Funktionen“ mit Definitionsmenge
und Werten in der Allklasse.
Um die mengentheoretischen Probleme, die sich daraus ergeben, zu vermeiden,
betrachtet man nur noch den Graph der entsprechenden Funktion, genauer: Ein
funktionsartiger Graph ist eine Menge
von Paaren
,
so dass keine zwei Paare im ersten Eintrag übereinstimmen:
Definitions- und Wertemenge sind tatsächlich Mengen, aber es ist nicht nötig, sich von vornherein auf eine Zielmenge festzulegen, solange die Funktionen im Wesentlichen gleich sind.
Bei partiellen Funktionen gilt gleiches für den Ziel- und Quellbereich. Beide können einzeln oder zusammen echte Klassen sein; mengentheoretische Probleme entstehen nicht, solange der Graph eine Menge bleibt.
Symbolik
Für Funktionen gibt es etliche symbolische Schreibweisen, die jeweils einige spezielle Eigenschaften der Funktion ausdrücken. Im Folgenden werden einige wichtige genannt.
| Symbol | Erklärung |
|---|---|
| Funktion von | |
| Funktion, die | |
| Funktion, die | |
| Funktion, die | |
| Ausführlichste Notation, die alle beteiligten Mengen und die elementweise Zuordnung mit Beschreibung der Funktionssymbolik und der Formel o.Ä. zur Berechnung des Bildes angibt | |
| surjektive
Funktion (Surjektion) von | |
| injektive
Funktion (Injektion) von | |
|
|
bijektive
Funktion (Bijektion) von |
| Inklusionsabbildung,
natürliche Inklusion, natürliche Einbettung von ( | |
|
|
Identität, identische
Abbildung auf A oder von ( |
|
|
Isomorphismus
von |
| partielle Funktion (s.o.) von | |
| mehrwertige Funktion, Multifunktion, Korrespondenz
(s.o.) von | |
(bzw. |
Menge der Funktionen (bzw. partiellen Funktionen), … von |
Die Symbole können auch, wo sinnvoll, miteinander kombiniert werden.
Literatur
- Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. 4. Auflage. Spektrum, Akademischer Verlag, Heidelberg u.a. 2003, ISBN 3-8274-1411-3.
- Paul R. Halmos: Naive Mengenlehre (= Moderne Mathematik in elementarer Darstellung. Bd. 6). Übersetzt von Manfred Armbrust und Fritz Ostermann. 5. Auflage. Vandenhoeck & Ruprecht, Göttingen 1994, ISBN 3-525-40527-8.
- Adolf P. Youschkevitch: The Concept of Function up to the Middle of the 19th Century. In: Archive of the History of Exakt Sciences. 16 Springer Verlag, Berlin 1976.
Anmerkungen
- ↑
seltener in Anlehnung an die Mengenschreibweise
äquivalent
- ↑ a b c teilweise auch ohne die eckigen Klammern notiert
- ↑
beziehungsweise
entsprechend der vereinfachten Funktionsdefinition mit Funktion=Graph. Alternative Bezeichnungsweisen:
oder
für die Korrespondenz
zur Multifunktion
, im Fall
(Transitionsfunktion) auch
oder
für die Potenzmenge
von
- ↑
wie immer für zweistellige Relationen; wir fassen
die Funktion
als zweistellige Relation auf, erst recht ihre Umkehrung
- ↑
Die Notation
wird von manchmal abweichend für (beliebige) Relationen gebraucht.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.12. 2025