Regelstrecke

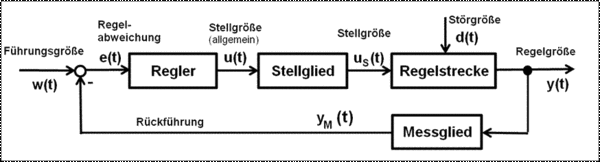
Blockschaltbild eines erweiterten Standardregelkreises. Die Störgröße kann an allen Teilen der Regelstrecke angreifen, meistens jedoch am Ausgang. Stellglied und Messglied müssen im Regelkreis berücksichtigt werden, wenn sie ein nicht vernachlässigbares Zeitverhalten haben oder von der idealen Kennlinie abweichen.

Als Regelstrecke bezeichnet man in der Regelungstechnik denjenigen Teil eines Regelkreises, der die zu regelnde physikalische Größe – die Regelgröße – enthält, auf die der Regler über die Stellgröße wirken soll. Bekannte Regelgrößen sind z.B. Raumtemperatur, Füllstand eines Behälters, Position einer Mechanik.

Die Regelstrecke kann als dynamisches System aus einer Kette von meist unbekannten Einzelsystemen bestehen, deren Ausgangsgröße über ein Messglied gemessen und über einen Soll- Istwertvergleich an den Regler zurückgeführt wird. Das Stellglied als Schnittstelle zwischen Regler und Regelstrecke kann Bestandteil der Regelstrecke, des Reglers oder ein eigenständiges Gerät sein. Eine Steuerstrecke wird zu einer Regelstrecke, wenn sie in einen Regelkreis einbezogen wird.

Mathematisch wird die Regelstrecke als Übertragungssystem definiert. Sie kann aus einem oder aus mehreren Übertragungssystemen und aus Eingrößen- und Mehrgrößensystemen (MIMO) bestehen. Die Übertragungssysteme können lineares und nichtlineares Verhalten aufweisen. Dementsprechend sind die mathematischen Beschreibungen der Regelstrecke unterschiedlich.

Lineare Übertragungssysteme (Lineares zeitinvariantes System) können durch Differentialgleichungen, durch Übertragungsfunktionen, durch numerische zeitdiskrete Methoden (Differenzengleichungen) und im Zustandsraum beschrieben werden.

Nichtlineare Übertragungssysteme wie Signalbegrenzungen und Systeme mit nichtlinearen Kennlinien können in Form von Tabellen (Matrizen) mit numerischen zeitdiskreten Methoden oder in der Zustandsraumdarstellung beschrieben werden. Totzeitsysteme können mit der komplexen Frequenz beschrieben oder mit numerischen zeitdiskreten Methoden berechnet werden.

Um den Regler für anspruchsvolle Regelaufgaben auslegen zu können, ist es nötig, die Regelstrecke zu identifizieren. Dies geschieht über die Erstellung eines mathematischen Modells der Regelstrecke, das möglichst genau das zeitliche Verhalten der Regelstrecke wiedergeben soll. Lässt sich das Modell nicht berechnen, kann als Identifizierungsmethode (siehe Identifizierung Regelstrecke) die Regelstrecke durch ein geeignetes Testsignal angeregt und das Ausgangssignal aufgezeichnet werden. Das zeitliche Verhalten dieser Signale erlaubt die Identifizierung zu einem Streckenmodell.

Charakterisierung der Regelstrecken

Die allgemeine Form einer Differentialgleichung für ein lineares zeitinvariantes Übertragungsglied (lineares zeitinvariantes System) mit u(t) als Eingangsgröße und y(t) als Ausgangsgröße und konstanten Koeffizienten lautet:

$a_{n}\cdot y^{(n)}(t)+\cdots a_{3}\cdot y'''(t)+a_{2}\cdot y''(t)+a_{1}\cdot y'(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)+b_{1}\cdot u'(t)+b_{2}\cdot u''(t)+b_{3}\cdot u'''(t)\cdots +b_{m}\cdot u^{(m)}(t)$

Der höchste Grad der Ableitung von y(t) gibt die Anzahl der Systemspeicherelemente der Strecke wieder.

Für alle Eingangssignale wird vorausgesetzt, dass sie für t<0 verschwinden. Damit kann das einseitige Laplace-Integral verwendet werden. Mit Hilfe der Laplace-Transformation lässt sich eine Zeitfunktion f(t) in eine Bildfunktion F(s) zuordnen.

Für die Transformation aus dem Zeitbereich in den s-Bereich existieren mehrere Lehrsätze wie Verschiebesatz, Dämpfungssatz, Differentiationssatz, Integrationssatz, Faltungssatz, Grenzwertsätze. Diese Laplace-Lehrsätze sind in jedem Fachbuch der Regelungstechnik beschrieben.

Anwendung der Übertragungsfunktion

Wird die Differentialgleichung eines Übertragungssystems mittels des Laplace-Differentiationssatzes in den s-Bereich (auch Bildbereich) transformiert, entsteht die allgemeine Form der Übertragungsfunktion G(s) als eine rational gebrochene Funktion in Polynom-Darstellung.

Die Übertragungsfunktion ist definiert als das Verhältnis von Ausgangssignal Y(s) zu Eingangssignal U(s) eines Systems als Funktion der komplexen Frequenz :

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}+b_{1}\cdot s+b_{2}\cdot s^{2}+b_{3}\cdot s^{3}+\cdots +b_{m}\cdot s^{m}}{a_{0}+a_{1}\cdot s+a_{2}\cdot s^{2}+a_{3}\cdot s^{3}+\cdots +a_{n}\cdot s^{n}}}={\frac {\text{Zählerpolynom (s)}}{\text{Nennerpolynom (s)}}}$

Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n>m ein zeitverzögerndes asymptotisch stabiles System dar.

Es bestehen mehrere Wege, die zu einer Übertragungsfunktion G(s) führen:

Laplace-Transformation der systembeschreibenden gewöhnlichen Differentialgleichung,
aus dem Signalverhältnis , wenn dieses bekannt ist,
durch Messen des Frequenzgangs $G(j\omega )$ ,
Spannungsteiler aus einem rückwirkungsfreien Impedanzverhältnis, (Beispiel: RC-beschalteter Operationsverstärker),
durch Systemidentifikation mittels Sprung- oder Impulsantwort.

Die Übertragungsfunktion G(s) ist eine abstrakte nicht messbare Größe und beschreibt das mathematische Verhalten eines linearen zeitinvarianten Systems im Frequenzbereich mit der komplexen Variable . Sie wird nach der Zerlegung der Zähler- und Nennerpolynome durch Nullstellenbestimmung in Produktterme (Linearfaktoren) erfolgreich eingesetzt für Systemanalyse, Systemsynthese, Systemstabilität und erlaubt die algebraische Behandlung von beliebig geschalteten rückwirkungsfreien Teilsystemen. Die Lage der Nullstellen und Polstellen einer Übertragungsfunktion in der s-Ebene $s=\delta +j\cdot \omega$ im Pol-Nullstellen-Diagramm ist eines der wichtigsten Kriterien zur Bestimmung der Stabilität eines Systems.

Die im komplexen Frequenzbereich (s-Bereich) definierten Übertragungssysteme haben folgende Bedeutungen:

$s=\delta +j\omega$ ist die unabhängige Variable im komplexen Frequenzbereich (Bildbereich, s-Bereich) mit $\delta$ als Realteil und $j\omega$ als Imaginärteil. Sie erlaubt beliebige algebraische Operationen im s-Bereich, ist aber nur ein Symbol für eine vollzogene Laplace-Transformation und enthält keinen Zahlenwert. Exponenten von s entsprechen dem Grad der Ableitung der Differentiale.
Zahlenwerte entstehen aus den Koeffizienten von und seinen Potenzen, indem die Polynome der s-Übertragungsfunktion durch Nullstellenzerlegung in Linearfaktoren (Produkte) zerlegt werden. Diese Nullstellen bzw. Pole können Null, real oder konjugiert komplex sein.

In der Zeitkonstantendarstellung der Linearfaktoren bestimmt die Zeitkonstante als dimensionslose Zahl nach der inversen Transformation das Zeitverhalten eines Teilsystems im Zeitbereich.

Fehlen die Grundglieder (Koeffizienten) $a_{0}$ oder $b_{0}$ der Übertragungsfunktion, wird der Linearfaktor $G(s)=s-0=s$ . Die Variable lässt sich aus dem Polynom freistellen und bedeutet je nach Lage im Zähler oder Nenner ein globales differenzierendes oder integrierendes Systemverhalten im Zeitbereich.
Linearfaktoren 2. Grades mit konjugiert komplexen Polen oder Nullstellen werden zur einfacheren Berechenbarkeit zu quadratischem Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.
Die Zählerordnung der Übertragungsfunktion darf nicht größer als die Nennerordnung sein. Es gilt $m\leq n$ mit zu Null angenommenen Anfangsbedingungen.

Faktorisierung der Übertragungsfunktion im s-Bereich

Mittels der Nullstellenbestimmung können die Polynome der Übertragungsfunktion G(s) in eine Produktform (Linearfaktoren) im Zähler und Nenner gebracht werden. Die Pole (Nullstellen des Nenners) oder Nullstellen (Nullstellen des Zählers) sind entweder Null, reell oder konjugiert komplex. Die Produktdarstellung im Zähler und Nenner der Übertragungsfunktion G(s) ist mathematisch identisch mit der Polynomdarstellung im Zähler und Nenner.

Für die Nullstellenbestimmung eines Polynoms bis 4. Ordnung sind im Internet fertige Programme unter dem Aufruf „Nullstellen (Lösungen) von Polynomen bestimmen“ zu finden. Für Systeme 2. Ordnung kann die „pq-Formel“: $x^{2}+px+q=0$ verwendet werden zur Berechnung von $x_{1},x_{2}$ der konjugiert komplexen Nullstellen.

Linearfaktoren der Pol-Nullstellendarstellung

Beispiel der Zerlegung der Polynome der Übertragungsfunktion durch die Pol- Nullstellungbestimmung in reelle Linearfaktoren:

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}+b_{1}\cdot s+b_{2}\cdot s^{2}+\cdots +b_{m}\cdot s^{m}}{a_{0}+a_{1}\cdot s+a_{2}\cdot s^{2}+\cdots +a_{n}\cdot s^{n}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}$

Da die Linearfaktoren des Zähler und Nenners der Übertragungsfunktion identisch sind, werden die Nullstellen und Polstellen zur vereinfachten Darstellung mit $s_{0}$ bezeichnet. Negative Realteile der Pole und Nullstellen der Linearfaktoren bedeuteten stabile Elementarsysteme, positive Realteile bedeuten instabile Elementarsysteme.

Bei den Linearfaktoren für reelle Pole und Nullstellen werden die negativen Zahlenwerte gleich gesetzt: Nullstelle $s_{01}=a$ (negativer Zahlenwert).

Bei den Linearfaktoren für Systeme 2. Ordnung mit reellen konjugiert komplexen Polen und Nullstellen haben die Zahlenwerte die Form: $s_{01/2}=a\pm j\omega$ mit a = Realteil, $\pm j\omega =$ Imaginärteile.

Liegen Zahlenwerte der Polynome der Übertragungsfunktion vor, können mit der Nullstellenbestimmung folgende Formen der Linearfaktoren entstehen:

bei fehlenden Absolutgliedern (Koeffizienten) $a_{0};b_{0}$ der Übertragungsfunktion:

$G_{1}(s)=s$

bei reellen Polen und Nullstellen:

$G_{2}(s)=s-s_{0}=s+a$ $|\qquad {\text{mit}}\ a=-s_{0}$ = Realteil.

bei Systemen 2. Ordnung mit konjugiert komplexen Polen und Nullstellen:

$G_{3}(s)=s-s_{0}=s+a\pm j\omega$ $|\qquad {\text{mit}}\ a=-s_{0}$ = Realteil, $\pm j\omega$ = Imaginärteile.

Diese Linearfaktoren werden zur einfacheren Berechenbarkeit zu quadratischem Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.

$G_{3}(s)=(s+a+j\omega )\cdot (s+a-j\omega )=s^{2}+2\cdot a\cdot s+a^{2}+\omega ^{2}:=s^{2}+p\cdot s+q\ {\bigg |}\qquad p=2a;\ \ q=a^{2}+\omega ^{2}$ .

Linearfaktoren der Zeitkonstantendarstellung

Die Linearfaktoren der Pol- Nullstellen-Darstellung können auch als Zeitkonstantendarstellung definiert werden, in dem die Zahlenwerte der Pole oder Nullstellen als Quotient $T=1/a$ definiert werden. ( $-s_{0}=a$ )

$\underbrace {(s-s_{0})} _{\text{Produktterm}}=\underbrace {(s+a)} _{a={\text{negativer Wert}}}=\underbrace {k\cdot (T\cdot s+1)} _{\text{Zeitkonstantendarstellung}}$

Aus dem Linearfaktor 1. Ordnung $G_{2}(s)=s+a$ wird in der Zeitkonstantendarstellung:

$G_{2}(s)=k\cdot (T\cdot s+1)$ , in der alle Terme positiv sind.

Ein Faktor $k=a$ berücksichtigt, dass die Pol-Nullstellen-Darstellung und die Zeitkonstantendarstellung mathematisch identisch sein müssen.

Aus dem quadratischen Linearfaktor 2. Ordnung gilt in der Zeitkonstantendarstellung die Normalform:

$G_{3}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1$

mit D = Dämpfungsgrad.

Die faktorisierte Zeitkonstantendarstellung ist üblich und anschaulicher. Alle Terme der Übertragungsfunktion sind bei stabilen Systemen stets positiv.

Die Linearfaktoren im Nenner der Übertragungsfunktion G(s) bestimmen für ein gegebenes Eingangssignal U(s) das Zeitverhalten f(t) des Teilsystems. Die Linearfaktoren im Zähler haben nur Einfluss auf die Größe der Amplitude des Ausgangssignals y(t) .

In der linearen Regelungstechnik können alle Übertragungsglieder aus folgenden drei Grundformen zusammengesetzt werden. Sie haben eine völlig unterschiedliche Bedeutung, ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen. Weiterhin unterscheiden sie sich darin, ob es sich um reguläre oder um die nur selten natürlich vorkommenden nichtregulären Systeme handelt.

Die Linearfaktoren mit negativen Realteilen der Pole und Nullstellen kennzeichnen folgende stabile Elementarsysteme:

Typ Linearfaktor Pol-Nullstellen-Darstellung	Typ Linearfaktor Zeitkonstanten-Darstellung	Bedeutung im Zähler	Bedeutung im Nenner
$G_{1}(s)=s+0=s$ Absolutglied a₀ oder b₀ fehlt,	$G_{1}(s)=s$ Nullstelle oder Pol	Differenzierer, D-Glied	Integrator, I-Glied
$G_{2}(s)=s+a$ $a=-s_{0}$ ; reelle Nullstelle	$G_{2}(s)=k\cdot (T\cdot s+1)$ mit $T=1/a,\quad k=a$	$PD_{1}$ -Glied	Verzögerung, $PT_{1}$ -Glied
Quadratischer Linearfaktor: $G_{3}(s)=s^{2}+2\cdot a\cdot s+a^{2}+\omega ^{2}$ $G_{3}(s):=s^{2}+p\cdot s+q$ mit $\ p=2\cdot a,\quad q=a^{2}+\omega ^{2}$	Normalform: $G_{3}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1$ mit $T={\sqrt {T^{2}}};\quad D={\frac {2DT}{2T}}$	$PD2_{kk}$ -Glied für 0 < D < 1 mit konjugiert komplexen Nullstellen. Anwendung: Vorfilter der Führungsgröße	Schwingungsglied, $PT2_{{kk}}$ -Glied für 0 < D < 1 mit konjugiert komplexen Polen.

Dabei ist die Zeitkonstante, die komplexe Frequenz, der Dämpfungsgrad.

Sind die Zahlenwerte der Pole und Nullstellen positiv, ergeben sich folgende instabile Übertragungssysteme in der Zeitkonstantendarstellung:

Typ Linearfaktor Zeitkonstanten-Darstellung	Bedeutung im Zähler	Bedeutung im Nenner
Nichtreguläres System 1. Ordnung $G_{2}^{*}(s)=T\cdot s-1$	Instabiles Übertragungsglied mit positiver Nullstelle (keine technische Bedeutung)	Instabiles nichtreguläres Übertragungsglied mit einer positiven Polstelle. Als Übergangsfunktion monoton steigende Amplitude.
Nichtreguläres System 2. Ordnung $G_{3}^{*}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s-1$	Instabiles Übertragungsglied 2. Ordnung mit einer negativen und positiven Nullstelle (keine technische Bedeutung)	Instabiles Schwingungsglied mit einer negativen und positiven Polstelle. Als Übergangsfunktion monoton steigende Schwingamplitude.

Diese nichtregulären Linearfaktoren haben ein nichtlineares Ein- Ausgangsverhalten und können als mathematische Modelle der Mitkopplung (positive Rückkopplung) als Hystereseeffekte verstanden werden. Die nichtregulären Linearfaktoren sind in Kombination mit regulären Linearfaktoren algebraisch berechenbar. Gleiche nichtreguläre Teilsysteme mit gleichen Zeitkonstanten dürfen aus dem Zähler und Nenner einer Übertragungsfunktion nicht gekürzt werden. Regelkreise mit einem nichtregulären Teilsystem der Regelstrecke können bei geeigneter Reglerparametrierung problemlos stabil werden.

Tabellarische Darstellung des Systemverhaltens von Linearfaktoren 1. und 2. Ordnung im Nenner der Übertragungsfunktion

Benennung →	PT1-Glied	I-Glied Grenzstabil	Instab. T1-Glied Monoton instab.	PT2_KK-Glied Oszillatorisch gedämpft	PT2_KK-Glied Oszillat. grenzstabil	Instab. T2_KK-Glied Oszillatorisch instabil
Übergangsfunktion → (Sprungantwort) Diagramme numerisch berechnet $\Delta t=0{,}01$ [s]
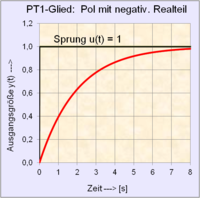Polstellen →	$s_{p}=-0{,}5$	$s_{p}=0$	$s_{p}=0{,}5$	$s_{p1/2}=-0{,}25\pm j\cdot 1{,}98$	$s_{p1/2}=0\pm j\cdot 2{,}0$	$s_{p1/2}=0{,}25\pm j\cdot 1{,}98$
Übertragungsfunktion → $Y(s)=G(s)\cdot {\frac {1}{s}}=$ als Sprungantwort	${\frac {1}{s\cdot (2\cdot s+1)}}$	${\frac {1}{s\cdot s}}$	${\frac {1}{s\cdot (2\cdot s-1)}}$	${\frac {1}{s\cdot (0{,}25s^{2}+0{,}125s+1)}}$	${\frac {1}{s\cdot (0{,}25s^{2}+1)}}$	${\frac {1}{s\cdot (0{,}25s^{2}-0{,}125s+1)}}$

Partialbruch-Darstellung

Mit der in jedem Fachbuch der Regelungstechnik befindlichen Korrespondenz-Tabelle der Laplace-Transformation können Terme der Übertragungsfunktion G(s) der Produktdarstellung in den Zeitbereich f(t) transferiert werden. Für nicht in den Korrespondenztabellen behandelte Übertragungsfunktionen können die Übertragungsfunktionen der Produktdarstellung mittels Partialbruchzerlegung in additive Terme zerlegt werden, deren einfache Zeitfunktionen bekannt sind.

Dazu muss das Nennerpolynom N(s) einer Übertragungsfunktion G(s) in folgende Form faktorisiert werden. Die Pole der Übertragungsfunktion bestimmen die Partialbrüche:

$G(s)={\frac {Z(s)}{N(s)}}={\frac {Z(s)}{(s-s_{p1})(s-s_{p2})\dotsb (s-s_{pn})}}=\sum _{i=1}^{n}{\frac {A_{i}}{(s-s_{pi})}}$

Partialbruch-Darstellung für reelle Pole und Nullstellen mit Absolutglied:

$G(s)={\frac {A_{1}}{s-s_{p1}}}+{\frac {A_{2}}{s-s_{p2}}}+\dotsb +{\frac {A_{n}}{s-s_{pn}}}$

Die unbekannten Parameter $A_{1}\dotsb A_{n}$ lassen sich durch Koeffizientenvergleich ermitteln.

Ein Produktterm eines einfachen $PT_{1}$ -Verzögerungsgliedes einer Übertragungsfunktion mit der Polstelle kann unmittelbar in den Zeitbereich überführt werden:

${\frac {1}{s+a}}\ \bullet \!\!-\!\!\circ \ e^{-at}\ {\bigg |}$ (Impulsantwort)

Für Übertragungsfunktionen mit den verschiedenen Formen der Linearfaktoren kann die Berechnung der Partialbrüche aufwendig werden.

Grundsätzlich einfacher gestaltet sich die Berechnung des Ausgangssignal eines dynamischen Systems f(t) bei gegebenem Eingangssignal U(s) , wenn die Linearfaktoren F(s) in Differenzengleichungen $f(\Delta t)$ umgesetzt werden und diese numerisch gelöst werden.

Frequenzgang

Der Frequenzgang ist ein Spezialfall der Übertragungsfunktion. Er kennzeichnet das Verhalten eines Systems mit erzwungener Dauerschwingung und der imaginären Frequenz $s=j\cdot \omega$ . Frequenzgang und Übertragungsfunktion unterscheiden sich nur durch die Entstehungsweise.

Alle Formen der Linearfaktoren (hier in Zeitkonstantendarstellung):

$G_{1}(s)=s;\quad G_{2}(s)=Ts+1;\quad G_{3}(s)=T^{2}s^{2}+2DTs+1$

des Zählers und des Nenners können ohne Informationsverlust auch als Frequenzgang $G(j\omega )$ mit $\delta =0$ grafisch im Bode-Diagramm oder als Ortskurve des Frequenzgangs dargestellt werden und dienen der Stabilitätsbetrachtung und der Systemanalyse.

Schaltung von Regelkreisgliedern

Übertragungsglieder können verschaltet werden als:

Reihenschaltung: $G(s)=G1(s)\cdot G2(s)$

Es gilt das Prinzip der ungestörten Superposition. Die Systeme in Produktdarstellung können in der Reihenfolge z.B. innerhalb eines offenen Regelkreises beliebig verschoben werden.

Das Superpositionsprinzip für den offenen Regelkreis gilt nicht, wenn

innerhalb der Regelstrecke Begrenzungen wirksam werden (nichtlineares Verhalten)
innerhalb des Reglers - was sehr häufig vorkommt - Begrenzungen wirken (nichtlineares Verhalten)
der Angriffspunkt einer Störgröße z.B. am Eingang der Regelstrecke liegt. (Begründung: Die Zähler der Stör-Übertragungsfunktionen bei der Verschiebung einer Komponente des Reglers vor oder hinter den Angriffspunkt der Störgröße sind nicht identisch)

Parallelschaltung: $G(s)=G1(s)\pm G2(s)$ ,
Gegen- und Mitkopplung: $G(s)={\frac {G1(s)}{1\pm G1(s)\cdot G2(s)}}$

Die faktorielle Darstellung der Grundglieder in der Reihenschaltung ist sehr vorteilhaft, weil sämtliche Daten für die Kriterien der Stabilität wie Pole, Nullstellen, Verstärkung und Zeitkonstanten sich aus den Übertragungsfunktionen der Regelkreisglieder ableiten lassen. Gleiche differenzierende und verzögernde Grundformen der Übertragungsfunktionen mit gleichen Zeitkonstanten kompensieren sich zu G(s) = 1.

Regelstreckenarten

Man unterscheidet lineare Regelstrecken und nichtlineare Regelstrecken. Bei linearen Regelstrecken unterscheidet man Regelstrecken mit Ausgleich, ohne Ausgleich und instabile Regelstrecken.

Bei Regelstreckengliedern mit Ausgleich erreicht die Ausgangsgröße y(t) nach genügend langer Zeit die Eingangsgröße u(t). Beide Größen unterscheiden sich für $t\to \infty$ nur durch den Proportionalitätsfaktor K. $y(t)\sim u(t)$ .
Unter linearen Regelstreckengliedern ohne Ausgleich versteht man Regelstrecken mit I-Verhalten (I-Glied). Dabei strebt die Ausgangsgröße y(t) bei sprungförmiger Eingangsgröße u(t) nach genügend langer Zeit einen unendlich großen Wert an.

Formal sind diese Regelstrecken mit einem I-Glied damit grenzstabil, der Wert der Ausgangsgröße bleibt gespeichert, wenn die Eingangsgröße u(t) zu Null wird.

Ein I-Glied erfüllt den Begriff der „Internen Stabilität“, ist aber nicht „Extern stabil“, weil seine Ausgangsgröße für eine gegebene Eingangsgröße unbeschränkt steigt.

Instabile Regelstrecken erkennt man an der Art der Polstellen. Sie liegen in der rechten s-Halbebene und haben einen positiven Realteil. Die Übertragungsfunktion in Produktdarstellung hat einen negativen Koeffizienten. Das Polynom der charakteristischen Gleichung der Übertragungsfunktion kann trotz positiver Koeffizienten positive Pole enthalten und damit instabil sein.

Lineare Regelstrecken

P-Regelstrecke

Der Ausgang eines P-Gliedes ist proportional zum Eingang. Ein Spannungsteiler oder die Untersetzungen in Hydrauliksystemen sind Beispiele für P-Regelstrecken.

Verzögerungsglied 1. Ordnung (PT1-Glied)

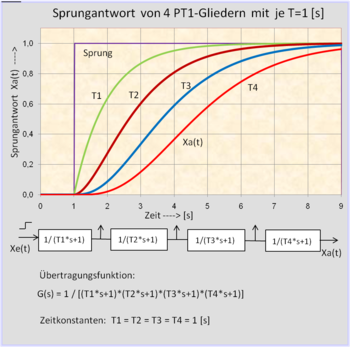
Die Sprungantworten Xaσ(t) mit 4 PT1-Gliedern mit je gleichen Zeitkonstanten mit je T = 1[s]

Das PT1-Glied kommt in der Natur und in der Technik am häufigsten vor. Es entsteht z.B., wenn Wärme in ein Medium fließt oder Spannung an ein RC-Glied angelegt wird. Das PT1-Glied ist ein System mit Ausgleich.

Differentialgleichung:

$T\cdot y'(t)+y(t)=K\cdot u(t)\quad \quad y(t)={\frac {1}{T}}\int K\cdot (u-y)\cdot dt$

Übertragungsfunktion:

$G(s)={\frac {Y(s)}{U(s)}}=K\cdot {\frac {1}{T\cdot s+1}}$

Siehe auch Bode-Diagramm und Ortskurve des Frequenzgangs unter PT1-Glied!

Verzögerungsglied 2. Ordnung (PT2-Glied)

Wenn ein Nennerpolynom der Normalform $T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1\,$ in Faktoren mit Hilfe der Formel zur Lösung gemischt quadratische Gleichungen aufgelöst werden kann, entstehen zwei PT1-Glieder in Reihenschaltung. Das PT2-Glied ist ein System mit Ausgleich.

Differentialgleichung: $T^{2}\cdot y''(t)+T\cdot y'(t)+y(t)=K\cdot u(t)$

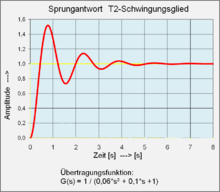
Übertragungsfunktion: $G(s)=K\cdot {\frac {1}{(T1\cdot s+1)\cdot (T2\cdot s+1)}}$

Darstellung der Sprungantwort eines PT2-Schwingungsgliedes

Wenn das Nennerpolynom der oben genannten Form für die Dämpfung D einen Wert 0 < D < 1 hat, hat das System konjugiert komplexe Pole. Diese Form des PT2-Gliedes bezeichnet man als Schwingungsglied:

Übertragungsfunktion: $G(s)=K\cdot {\frac {1}{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}\quad \quad \quad \quad 0<D<1$

Schwingungsglieder entstehen durch Energieaustausch von zwei speicherfähigen Verzögerungsgliedern 1. Ordnung, wie Feder-Masse-Systeme, LC-Schwingkreis.

Die Grafik zeigt die Sprungantwort eines Schwingungsgliedes mit der Übertragungsfunktion:

$G(s)={\frac {1}{0{,}06\cdot s^{2}+0{,}1\cdot s+1}}$ , der Dämpfungsgrad beträgt D = 0,22

Siehe auch Bode-Diagramm und Ortskurve des Frequenzgangs unter PT2-Glied!

Integrierendes Übertragungsglied (I-Glied)

Typisches Beispiel für ein I-Glied ist der Zufluss einer Flüssigkeit in einen Behälter oder das Aufladen eines Kondensators mit einstellbarem Konstantstrom.

Das I-Glied ist ein System ohne Ausgleich, die Ausgangsgröße steigt als Funktion einer beliebigen, konstanten Eingangsgröße monoton an.

Wegen der Lage des Pols in der s-Ebene bezeichnet man es auch als grenzstabil.

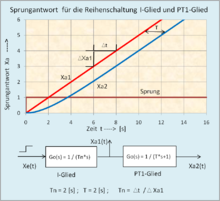
Die Sprungantworten Xaσ(t) an einer Reihenschaltung mit einem I-Glied G(s) = 1 / (Tn*s) und einem PT1-Glied G(s)= 1/(T*s+1). Die Eingangsgröße des PT1-Gliedes Xa1(t) entspricht der Anstiegsfunktion.

Es unterscheidet sich dadurch von einem PT1-Glied, dass in der linearen Differentialgleichung der Beiwert $a_{0}=0$ ist.

Die allgemeine Differentialgleichung: $\cdots a_{2}\cdot y''(t)+a_{1}\cdot y'(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)\cdots ,\quad$

wird für das I-Glied zu:

$a_{1}\cdot y'(t)=b_{0}\cdot u(t)\qquad y(t)={\frac {1}{T_{n}}}\int (u)\cdot dt$

Übertragungsfunktion mit $T_{n}=a_{1}/b_{0}$ , $T_{n}=$ Nachstellzeit:

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}}{a_{1}\cdot s}}={\frac {1}{T_{n}\cdot s}}$

Siehe auch Bode-Diagramm und Ortskurve des Frequenzgangs unter I-Glied!

Instabile Regelstrecken

Instabile Regelstrecken können entstehen z.B. durch:

zwei oder mehrere in Reihe geschaltete I-Glieder
Rückkopplung im Funktionsplan (Wirkungsplan) der Strecke. Wird z.B. das Ausgangssignal eines positiv verstärkenden I-Gliedes auf den Eingang mit positivem Vorzeichen zurückgekoppelt, so entsteht ein instabiles Übertragungsglied 1. Ordnung.

Sie können in der Natur entstehen, wenn auf die Lage von Körpern Beschleunigungskräfte einwirken, wie sie z.B. durch die Gravitation oder durch den Magnetismus hervorgerufen werden, dann wird die Lage zunehmend beschleunigt. Die Ausgangsgröße y(t) wächst progressiv bis zu einer natürlichen Begrenzung.

Die Stabilisierung solcher Strecken hat in der Industrie eine zunehmende Bedeutung. In der Fachliteratur werden Berechnungsbeispiele zu instabilen Regelstrecken immer häufiger dargestellt. Anwendungen sind Inverses Pendel (Transport aufrechtstehender Rakete auf dem Wagen, Ladebrücke beim Schiff oder Güterzug), „Magnetschwebekörper“ (Positionierung beim Anfahren einer Magnetschwebebahn). Häufig haben diese instabilen Regelstrecken auch nichtlineare Komponenten, wie zum Beispiel in chemischen Reaktoren mit exothermer Reaktion.

Instabiles Übertragungsglied 1. Ordnung

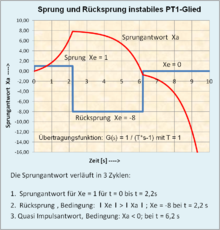
Sprungantwort eines instabilen Gliedes erster Ordnung bei einem Sprung und einem Rücksprung am Eingang

Dieses Übertragungsglied wird manchmal umgangssprachlich auch als 'instabiles PT1-Glied' bezeichnet. Diese Bezeichnung ist jedoch formal inkorrekt, da bei einem instabilen Übertragungsglied kein proportionales Verhalten vorliegen kann, weil sich die Ausgangsgröße nicht auf einen Endwert einstellt.

Die Differentialgleichung mit einem negativen Koeffizienten lautet z.B.:

$T\cdot y'(t)-y(t)=K\cdot u(t)$

Die Übertragungsfunktion lautet:

$G(s)={\frac {Y(s)}{U(s)}}=K\cdot {\frac {1}{T\cdot s-1}}$

Die Sprungantwort lautet:

$y(t)=K\cdot u\cdot (e^{t/T}-1)\,$

Das Zeitverhalten eines instabilen Gliedes 1. Ordnung mit einem Testsignal wird wie folgt beschrieben:

Eine Impulsfunktion oder eine Sprungfunktion beliebiger Amplitude startet unverzüglich das Ausgangssignal, das bis zu einer natürlichen Grenze exponentiell zunimmt.
Innerhalb des Arbeitsbereichs kann das Ausgangssignal nur dann in die entgegengesetzte negative Richtung gestartet werden, wenn ein negatives Eingangssignal – eine Sprungfunktion – im Betrag größer ist, als der momentanen positive Betrag der Impuls- bzw. Sprungantwort. Dies erklärt sich aus dem Prinzip der Mitkopplung.
Wenn die negative Sprungfunktion solange ansteht, dass die Sprungantwort auch negativ wird, kann die Sprungfunktion zu Null werden. Die Sprungantwort läuft dann selbständig weiter bis zu einer Begrenzung in negativer Richtung.

Diese Regelstrecke ist relativ leicht mit einem PI-Regler zu regeln.

Instabiles Übertragungsglied 2. Ordnung

Wenn im Nenner eines Übertragungsgliedes 2. Ordnung negative Koeffizienten stehen, oder die Dämpfung D = 0 ist, so ist das System instabil. Liegen konjugiert komplexe Pole vor, schwingt das System mit zunehmender Amplitude. Enthält der Zähler der Übertragungsfunktion keine Potenz von s höher als 0. Ordnung, wird oft aufgrund der Ähnlichkeit der Übertragungsfunktion zu einem PT2-Glied von einem 'instabilen PT2-Glied' gesprochen. Formal ist diese Bezeichnung jedoch falsch, da die Ausgangsgröße des instabilen Übertragungsglieds erster Ordnung gegen keinen endlichen Wert konvergiert, also kein proportionales Verhalten aufweisen kann.

Lautet die Übertragungsfunktion eines instabilen Übertragungsglieds 2. Ordnung z.B.:

$G(s)={\frac {K}{T1\cdot T2\cdot s^{2}+(T2-T1)\cdot s-1}}$

Falls das Nennerpolynom der Übertragungsfunktion keine konjugiert komplexen Pole hat, d.h. die Dämpfung D beträgt $D\geq 1$ , dann lässt sich das Polynom in ein PT1-Glied und ein instabiles Übertragungsglied erster Ordnung oder in zwei instabile Übertragungsglieder erster Ordnung zerlegen. Z.B.

$G(s)={\frac {K}{(T1\cdot s+1)\cdot (T2\cdot s-1)}}$

Das gleiche Ergebnis ergibt sich für die Übertragungsfunktion, wenn T1 = T2 = T für

$G(s)={\frac {K}{T^{2}\cdot s^{2}-1}}={\frac {K}{(T\cdot s+1)\cdot (T\cdot s-1)}}$

Diese instabile Regelstrecke ist ebenfalls relativ leicht mit einem PID-Regler zu regeln.

Totzeitglied

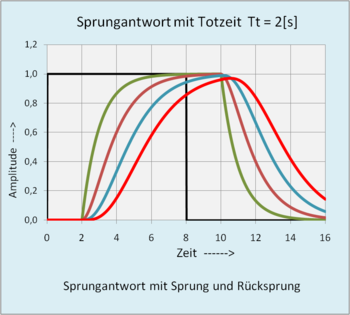
Sprungantwort von einem Sprung und einem Rücksprung eines Systems mit Totzeit T_t = 2 [s] und 4 in Reihe geschalteten Verzögerungsgliedern mit je T = 1 [s]

Das Totzeitglied ist ein in der Praxis häufig vorkommendes Übertragungsglied und wirkt meist in Verbindung mit weiteren Verzögerungsgliedern. Es wird durch reine Laufzeit bzw. Transportzeit eines Signals verursacht. Es verhält sich wie ein P-Glied, dessen Ausgangsgröße verspätet um die Totzeit ankommt, ohne die Eingangsgröße während dieser Zeit zu verzerren. Jede Änderung der Eingangsgröße wirkt um die Totzeit verspätet am Ausgang.

Zeitverhalten:

$\displaystyle y(t)={u}(t-T_{t})$

Sprungantwort:

$y(t)=0;\quad {\text{für}}\quad t<T_{t}\;$ ,

$y(t)=1;\quad {\text{für}}\quad t\geq T_{t}\;$ .

Übertragungsfunktion:

$G(s)={\frac {Y(s)}{U(s)}}=e^{-s\cdot T_{t}}$

Nichtlineare Übertragungssysteme

Beispiele nichtlinearer Übertragungssysteme

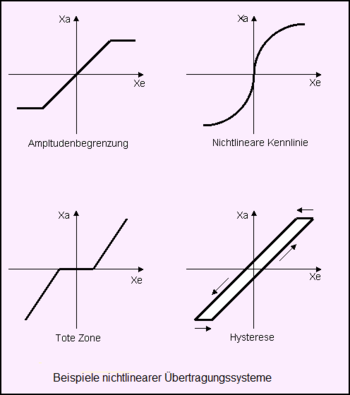
Bei linearen Übertragungssystemen ist die Ausgangsgröße im eingeschwungenen Zustand der Eingangsgröße stets proportional. Bei nichtlinearen Systemen wirkt mindestens eine nichtlineare Funktion in Verbindung mit linearen Systemen. Diese nichtlinearen Funktionen werden nach stetigen und unstetigen Nichtlinearitäten unterschieden. Sie können als Signal- bzw. Stellgrößenbegrenzungen, als stetige Nichtlinearität z.B. mit quadratischem Verhalten, als Funktionen mit begrenzter Ansprechempfindlichkeit (Tote Zone) bei Messfühlern und/oder mit Hysterese behaftet sein. Theoretische Untersuchungen der Stabilität von Regelkreisen mit Nichtlinearitäten können sehr aufwendig sein. Zur einfacheren Bestimmung des dynamischen Verhaltens und der Stabilität eines Regelkreises kann ein bestimmter Bereich um den Arbeitspunkt eines nichtlinearen Übertragungssystems betrachtet werden. Gehen die dynamischen Abweichungen um den gewählten Arbeitspunkt hinaus, muss die gesamte Nichtlinearität in die Berechnung einbezogen werden.

Als Analysemethode kann unter anderem die Harmonische Balance angewendet werden. Mit der Gleichung der Harmonischen Balance werden die Beziehungen der Beschreibungsfunktion N(A) des statischen nichtlinearen Systems und des dynamischen linearen Systems $G_{0}(j\omega )$ in ein Verhältnis gesetzt. Daraus lassen sich die zwei kritischen Systemgrößen des harmonisch schwingenden Regelkreises – die Eingangs-Amplitude und die kritische Frequenz $\omega _{\mathrm {KRIT} }$ an der Stabilitätsgrenze – errechnen oder grafisch nach dem Zwei-Ortskurven-Verfahren bestimmen.

Laut der Fachliteratur können bis zu 40 unterschiedliche Beschreibungsfunktionen nichtlinearer statischer Systeme entnommen werden.

Signal- und Stellgrößenbegrenzung (Sättigung)

Diese nichtlineare Funktion kommt in der Praxis am häufigsten bei allen Übertragungssystemen vor. Ein Ventil kann nur zu 100 % geöffnet sein, und ein Elektromotor darf nicht über seine maximale Leistung betrieben werden. Begrenzungen des Reglers und der Strecke müssen wegen der Regeldynamik aufeinander abgestimmt sein, in der Weise, dass die Begrenzung des Reglers eine kleinere Stellgröße zulässt, als die Strecke verarbeiten kann. Signal- bzw. Stellgrößenbegrenzungen wirken dämpfend auf das Großsignalverhalten der Regelgröße. Liegt die Übertragungsfunktion einer offenen Regelstrecke mit den linearen Systemen vor, hilft die Simulation mit geeigneten Rechenprogrammen den Einfluss der Begrenzung darzustellen.

Nichtlineare stetige Kennlinie einer Regelstrecke

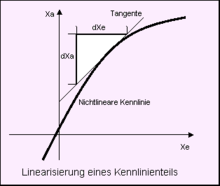
Linearisierung im Arbeitspunkt eines nichtlinearen Systems

Die quadratische Charakteristik einer Federkennlinie oder die nichtlineare Querschnittveränderung eines Ventils bedeuten in sonst mit linearen Systemen wirkenden Regelstrecken unterschiedliche Streckenverstärkungen. Wenn ein Regelkreis für einen festen Sollwert eingestellt ist, hat die Stellgröße einen bestimmten Arbeitsbereich innerhalb der nichtlinearen Funktion. Durch Anlegen einer Tangente an den Arbeitsbereich der nichtlinearen Funktion der Regelstrecke kann die Verstärkung der so linearisierten Teilkennlinie bestimmt werden. Mit der Verstärkung aus dem Quotienten $K={\frac {dy}{du}}$ der Tangente in diesem Arbeitspunkt kann das Verhalten des Regelkreises berechnet werden, wenn die Übertragungsfunktionen der übrigen Übertragungssysteme bekannt sind.

Sollen beliebige Sollwerte für einen gegebenen Regelkreises eingestellt werden, müssen die Parameter des Reglers für die größte Verstärkung der Nichtlinearität der Strecke optimiert werden, anderenfalls besteht bei zunehmender Streckenverstärkung die Gefahr der Instabilität des Regelkreises. Gleichzeitig ist damit ein schlechtes dynamisches Verhalten des Regelkreises verbunden, wenn die Nichtlinearität um den Arbeitspunkt eine geringere Verstärkung aufweist.

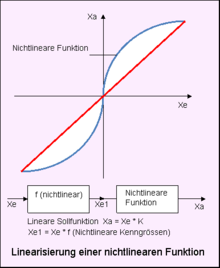
Linearisierung einer nichtlinearen Funktion mit einer Kompensationsfunktion

Abhilfe kann eine Kompensationsfunktion (Inverse Nichtlinearität) im Eingang des nichtlinearen Systems bringen. Für einen digitalen Regler wäre das nur eine Tabelle, die berücksichtigt werden muss, damit die Nichtlinearität zu einer linearen Funktion mit proportionalem Verhalten gewandelt werden kann. Die Kompensationsfunktion unterliegt nicht dem Superpositionsprinzip.

Unstetige Ansprechempfindlichkeit (Tote Zone)

Bei Messfühlern tritt manchmal der Effekt auf, dass eine bestimmte Größe des Messwertes überschritten werden muss, damit der Messfühler ein Signal abgibt. Für einen Regelkreis bedeutet dies, dass kleine Sollwerte und damit kleine Regelgrößen nicht eingestellt werden können.

Hysterese

Durch Reibung an Ventilen, durch magnetische Effekte z.B. bei Relais oder durch Mitkopplung an Operationsverstärkern kann der Hystereseeffekt auftreten. Die Hysterese kann stetiges oder unstetiges Verhalten haben. Für unstetige Regler ist die Hysteresefunktion erwünscht. Für die stetige Regelung ist der Hystereseeffekt sehr unerwünscht.

Testsignale

Den nichtperiodischen (deterministischen) Testsignalen kommt in der Regelungstechnik eine zentrale Bedeutung zu. Mit ihrer Hilfe ist es möglich, ein Übertragungssystem zu testen, auf Stabilität zu prüfen oder Eigenschaften zu ermitteln.

Den Testsignalen ist gemeinsam, dass sie zum Zeitpunkt t = 0 beginnen und bei t < 0 eine Amplitude = 0 aufweisen. Es wird das Testsignal als Eingangsgröße u(t) an einem Übertragungssystem und die Systemantwort als Ausgangsgröße y(t) in der nachfolgenden Tabelle dargestellt. Zur Unterscheidung der Funktion der Signale werden sie mit den Zeichen δ (Impuls), Ϭ (Sprung), a (Anstieg) und s (Sinus) indiziert.

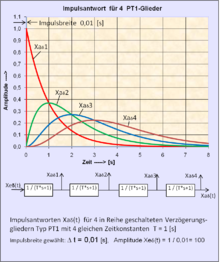
Die Impulsantwort Xaδ(t) von 4 hintereinander geschalteten PT1-Gliedern mit gleichen Zeitkonstanten

Der theoretische Deltaimpuls (δ-Impuls, Dirac-Impuls) für t = 0 mit unendlich großer Amplitude ist technisch nicht realisierbar. An seiner Stelle wird ein Rechteckimpuls mit der Impulsfläche 1 = Amplitude · Zeit definiert. In der Praxis genügt ein Wert für die Impulsdauer von Δt = 1 % bis 10 % der dominanten Zeitkonstante des zu prüfenden Übertragungssystems.

Systemantwort Xa(s) und Xa(t) der Testsignale: Die Testsignale im Bildbereich können mit einer Übertragungsfunktion eines Systems multipliziert werden. Bei der Rücktransformation in den Zeitbereich stellt sich die Antwort des Testsignals für das Übertragungssystem dar. Soll ein digitaler Rechner mittels numerischer Verfahren zur Lösung der Systemantwort herangezogen werden, kann für die nichtperiodischen Testsignale Xe die kontinuierliche Zeitvariable t durch eine Folge von n Zeitschritten (Diskretisierungszeit = Dt) durch t = n · Dt ersetzt werden.

Die Systemantwort einer Impulsfunktion Xaδ(t) im Zeitbereich stellt das Verhalten des Systems dar. Die Rücktransformation einer beliebigen Übertragungsfunktion f(s) in den Zeitbereich f(t) immer auch die Impulsantwort des Systems.

Die Differentiation der Sprungfunktion entspricht der Impulsfunktion. Die Integration einer Sprungfunktion entspricht der Anstiegsfunktion. Die Differentiation der Sprungantwort eines Übertragungssystems entspricht der Impulsantwort.

Die Sinusfunktion gehört zur Gruppe der periodischen Signale. Die Frequenz-variable Einspeisung eines Übertragungssystems erlaubt die Aufnahme des Amplituden- und Phasengangs des Systems. Mit Hilfe des Bode-Diagramms kann die Übertragungsfunktion des Systems bestimmt werden.

Begriff Testsignal u(t)	Zeitverhalten des Testsignals	Bildbereich	Systemantwort y(t)
Impulsfunktion δ oder Stoßfunktion, Deltaimpuls	Normierter Impuls = $\int _{0}^{\infty }{\hat {u}}_{\delta }\cdot \,dt=1;$ $\qquad$ $\qquad$ Impulsdauer = $\Delta t={\frac {1}{{\hat {u}}_{\delta }(t)}}$ Hauptanwendung: Erkennung des Systems, der Ordnung und der Stabilität	$u_{\delta }(s)=1\,$	Impulsantwort oder Gewichtsfunktion
Sprungfunktion σ	Einheitssprung: ${\hat {u}}_{\sigma }(t)=1\quad {\text{für}}\ t>0,\qquad u_{\sigma }(t)=0\quad {\text{für}}\ t<0$ Hauptanwendung: Erkennung des Systems	$u_{\sigma }(s)={\frac {1}{s}}$	Sprungantwort oder Übergangsfunktion
Anstiegsfunktion oder Rampe	Anstiegsfunktion: $u_{a}(t)=c\cdot t;\,$ $\qquad$ $\qquad$ Gradient: $c={\frac {\Delta \,u_{a}(t)}{\Delta \,t}}$ Hauptanwendung: Bestimmung der Nachlaufeigenschaften	$u_{a}(s)={\frac {1}{s^{2}}}$	Anstiegsantwort oder Rampenantwort
Sinusfunktion s	$u_{s}(t)={\hat {u}}_{s}\cdot \sin(\omega \cdot t)\,\qquad \omega =2\cdot \pi \cdot f\qquad T={\frac {1}{f}}$ Hauptanwendung: Aufnahme des Amplituden- und Phasengang eines Systems	$u_{s}(s)={\frac {\omega }{s^{2}+\omega ^{2}}}$	Frequenzgang

Experimentelle Systemidentifikation von Regelstrecken nach der Sprungantwort

Systeme 1. Ordnung

Einfache Regelstrecken, die durch ein System 1. Ordnung beschrieben werden, sind leicht durch die Sprungantwort des Systems zu identifizieren. Es gelten die grafischen Bilder des Kapitels „Lineare Regelstrecken“.

Verzögerungsglied 1. Ordnung (PT1-Glied)

Die Übergangsfunktion für t>0 zeigt bereits für einen verschwindend kleinen Zeitwert t einen verschwindend kleinen Ausgangswert y(t).

Im Gegensatz zur Übergangsfunktion von Verzögerungen 2. oder höherer Ordnung beträgt die Ausgangsgröße y(t) für einen verschwindend kleinen Zeitwert t immer y(t)=0. Dieses Verhalten kann man besonders gut beobachten bei den Impulsantworten mehrerer PT1-Glieder in der Reihenschaltung (→ siehe Grafik unter Kapitel Testsignale).

Die Funktion y(t) nähert sich asymptotisch an das Maximum der physikalischen Größe Y_max. Die Zeitkonstante T entspricht dem Zeitwert von t, der von 63 % von y_max als Schnittpunkt in der Funktion der Sprungantwort gebildet wird. Der Proportianalitätsfaktor der Strecke Ks(t) wird bestimmt aus y / u im Beharrungsverhalten.

Übertragungsfunktion: ${\frac {Y(s)}{U(s)}}={\frac {K_{s}}{T\cdot s+1}}$

Integrale Regelstrecke (I-Glied)

Die Sprungantwort- vorausgesetzt der Speicher des Systems ist leer - bildet eine monoton ansteigende Gerade, die durch den Ursprung des Koordinatensystem startet und erst durch natürliche Begrenzungen endet. Der Streckenbeiwert $K_{i}=1/T_{n}$ ergibt sich durch $K_{i}=\Delta y/\Delta t$ .

Übertragungsfunktion: ${\frac {Y}{U}}(s)={\frac {Ki}{s}}$

Kombinationen von PT1-Glied und I-Glied

Oberhalb des eingeschwungenen Zustandes (Beharrungsverhalten) des PT1-Systems kann eine Hilfslinie durch parallele Verschiebung direkt in den Ursprung gezogen werden und stellt das Verhalten des I-Gliedes dar. Eine waagerechte Linie eines Wertes im eingeschwungenen Zustand von y schneidet die beiden Kennlinien. Der waagerechte Abstand dieser Schnittpunkte entspricht der Zeitkonstante T des PT1-Gliedes. Die Kennwerte des I-Gliedes werden wie bereits definiert errechnet.

Übertragungsfunktion: ${\frac {Y(s)}{U(s)}}={\frac {Ki\cdot Ks}{s\cdot (T\cdot s+1)}}$

Instabiles Übertragungsglied 1. Ordnung

Die Zeitkonstante kann direkt aus der Sprungantwort abgelesen werden. Für den Sprung $U_{\text{max}}$ gilt:

Der Wert von $Y=U_{\text{max}}\cdot 0{,}63$ schneidet die Funktion der Sprungantwort in waagerechter Richtung. Die diesem Punkt zugehörige Zeit – Schnittlinie in senkrechter Richtung – ist gleich der Zeitkonstante .

Übertragungsfunktion: ${\frac {Y(s)}{U(s)}}={\frac {1}{T\cdot s-1}}$

Systeme höherer Ordnung

PT2-Schwingungsglied

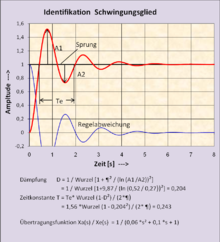
Identifikation eines PT2-Schwingungsgliedes durch die Amplituden der 1. und 2. Halbwelle

Ist die Sprungantwort dieses Systems grafisch gegeben, kann die Übertragungsfunktion des Schwingungsgliedes aus dem Amplitudenverhältnis der zwei ersten Halbwellen errechnet werden.

Zunächst wird die Dämpfung der Schwingung berechnet:

$D={\frac {1}{\sqrt {1+{\frac {\pi ^{2}}{\left(\ln {\frac {A1}{A2}}\right)^{2}}}}}}$

Die Zeitkonstante T errechnet sich aus der Periodendauer Te der 1. Schwingung und aus der Dämpfung D:

$T={\frac {Te\cdot {\sqrt {1-D^{2}}}}{2\cdot \pi }}$

Damit ergibt sich die Übertragungsfunktion zu:

${\frac {Y(s)}{U(s)}}={\frac {1}{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}$

Nichtschwingende Systeme höherer Ordnung

Es gibt eine Reihe von Faustformelverfahren, die aus der Sprungantwort der Regelstrecke mit angelegter Tangente im Wendepunkt der Funktion eine Näherung der Sprungantwortfunktion ermitteln.

Zeit-Prozentkennwert-Verfahren (Schwarze)

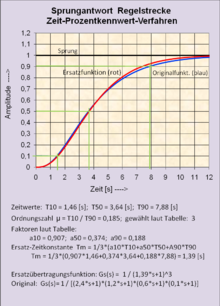
Identifikation einer Regelstrecke höherer Ordnung durch das Zeit-Prozentkennwert-Verfahren nach Schwarze

Mit der Methode des „Zeit-Prozentkennwert-Verfahrens“ wird zum Beispiel eine Modellstrecke ermittelt, die mit gleichen Zeitkonstanten je nach Streckenkonstanten beliebiger Ordnung tatsächlich eine sehr gute Annäherung an die reale Sprungantwort bietet (Zeitschrift Automatisierungstechnik, München 1993 von Latzel).

Für eine gegebene Sprungantwort einer nicht schwingenden Regelstrecke werden von den Amplitudenwerten Xa von 10 %, 50 % und 90 % der Maximalamplitude im Beharrungszustand die zugehörigen Zeitwerte T10, T50 und T90 erfasst und daraus eine Modell-Übertragungsfunktion aus n gleichen Verzögerungsgliedern gebildet.

Folgende Schritte sind erforderlich:

Aus dem Verhältnis μ = T10 / T90 wird mittels einer Tabelle die Ordnung des Streckenmodells festgelegt.
Aus derselben Tabelle werden Faktoren α10, α50 und α90 abgelesen.
Die für jede Ordnung gleiche Verzögerungszeit Tm der Modellstrecke berechnet sich zu:

$Tm={\frac {1}{3}}\cdot (\alpha 10\cdot T10+\alpha 50\cdot T50+\alpha 90\cdot T90)$

Damit liegt die Ordnung des Modellsystems und die für jede Ordnung gleiche Zeitkonstante fest.

In einer weiteren Tabelle (nach Latzel) kann man für die ermittelte Modellübertragungsfunktion zugleich die Reglerparameter für verschiedene Standardregler in Parallelstruktur ablesen.

Experimentelle Systemidentifikation durch frequenzvariable Einspeisung in die Regelstrecke

Wenn das Bode-Diagramm einer unbekannten Regelstrecke höherer Ordnung vorliegt, können durch Eintragung der Asymptoten in dem Amplitudengang die Streckenkonstanten ermittelt werden. Enthält die Regelstrecke auch eine Totzeit, wird auch der Phasengang der Regelstrecke benötigt.

Die Ermittlung des Bode-Diagramms und der Streckenkonstanten geschieht wie folgt:

Arbeitspunkt der Regelstrecke festlegen, z.B. auf 50 % des Arbeitsbereiches.
Auf den Arbeitspunkt eine sinusförmige variable Frequenz mit möglichst großer konstanter Amplitude so additiv einspeisen, dass keine Begrenzungseffekte am Ausgang der Regelstrecke auftreten. Die Frequenz wird in Schritten so verstellt, dass sich die Ausgangsamplitude von ungedämpft bis kleiner 1 % ändert.
Die z.B. auf den Wert 1 normierte Eingangsamplitude, die Ausgangsamplitude und die Phasenverschiebung der Ausgangsamplitude werden als Funktion der Frequenz tabellarisch erfasst. Das Amplitudenverhältnis wird in das Bode-Diagramm im logarithmischen Maßstab als Amplitudengang eingetragen. Beim Phasengang wird die Phase im linearen Maßstab eingetragen.
Nach Einzeichnen der Asymptoten (20 dB / Dekade für ein PT1-Glied) können die Eckfrequenzen $\omega _{E}={\frac {1}{T}}$ ermittelt werden. Mit dem Phasengang wird geprüft, ob die Summe der Anzahl der Zeitkonstanten (bzw. die Ordnung des Systems) mit der Summe der Phasenverschiebung (PT1-Glied 90° / Dekade) übereinstimmt.
Falls die Eckfrequenzen eng zusammenliegen, können diese nicht so genau bestimmt werden. Es empfiehlt sich in diesem Fall mit der gefundenen Übertragungsfunktion ein neues Bode-Diagramm zu erstellen und die beiden Amplitudengänge auf Deckungsgleichheit zu vergleichen und notfalls die vorher ermittelte Übertragungsfunktion zu korrigieren.

Experimentelle Identifikation einer Regelstrecke mit Hilfe einer Modellregelstrecke

Eine Regelstrecke kann man durch die Sprungantwort, durch die Impulsantwort der Regelstrecke oder auch durch Einspeisung einer variablen Frequenz identifizieren.

Wichtigste Merkmale für die Anwendung einer Modellregelstrecke mit Hilfe der Sprung- oder Impulsantwort sind:

Die Parameter einer Regelstrecke können mittels einer einfachen Modellregelstrecke ermittelt werden, indem die Kennlinie des Modells durch schrittweises Ändern der Zeitkonstanten des Modells auf die Kennlinie der unbekannten Regelstrecke angepasst wird.
Das Modell muss ähnliche Streckeneigenschaften aufweisen, wie die unbekannte Regelstrecke.

Bei Strecken ohne Ausgleich benötigt das Modell einen I-Anteil, bei Strecken mit Totzeit ist für das Modell ebenfalls ein Totzeitglied erforderlich.

Die Anpassung eines Modells an die unbekannte Regelstrecke mit Hilfe der Sprungantwort ist relativ einfach und kann evtl. auch grafisch durchgeführt werden.
Das Anpassung eines Modells an die unbekannte Regelstrecke mit Hilfe der Impulsantwort ist etwas aufwendiger, bietet aber bei Deckungsgleichheit der Kennlinien eine völlige Übereinstimmung zwischen Original und Modell in einem Regelkreis im Vergleich mit den jeweiligen Sprungantworten. Mit diesem Modell lässt sich auch die Ordnung des Originals feststellen.
Es sollte einfach zu realisieren sein.

Identifikation einer Regelstrecke mit Ausgleich und Totzeit durch die Sprungantwort

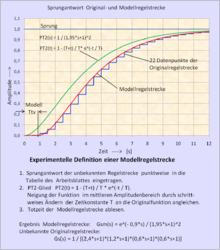
Sprungantwort einer Regelstrecke 4. Ordnung mit dominanter Zeitkonstante und deren Modellregelstrecke 2. Ordnung mit Totzeitglied

Die Sprungantwort hat den Vorteil der einfacheren Durchführung und des höheren Bekanntheitsgrades des zu erwartenden Ergebnisses. Die zeitunabhängige Streckenverstärkung Ks kann bei Regelstrecken mit Ausgleich im statischen Zustand direkt abgelesen werden.

Folgende Anforderungen werden an die Modellregelstrecke für eine Regelstrecke mit Ausgleich gestellt:

Die Sprungantwort der Modellregelstrecke soll weitgehend deckungsgleich mit der Originalregelstrecke sein.
Die Modellregelstrecke soll eine bestimmte Form der Übertragungsfunktion aufweisen, die sich mit einem guten linearen Standardregler – beispielsweise einem PID-Regler – leicht für eine Parametrierung des Reglers eignet.
Das Verfahren soll für Regelstrecken ab 2. Ordnung mit und ohne Totzeit anwendbar sein.

Ein PID-Regler in Produktdarstellung (Reihenschaltung) kann 2 PT1-Verzögerungen kompensieren. Deshalb wird folgende leicht zu bestimmende Form der Modellregelstrecke gewählt, die aus einem schwingungsfreien PT2-Glied und einem Totzeitglied besteht:

Übertragungsfunktion Modell:

$G_{sm}(s)={\frac {e^{-Ttv\cdot s}}{(T\cdot s+1)^{2}}}$

Ttv besteht aus einer eventuell vorhandenen Totzeit Tt und der durch die grafische Konstruktion – bzw. durch ein Simulationsprogramm – bedingten Verschiebezeit.

Die Sprungantwort des PT2-Gliedes lautet:

$G_{PT2}(t)=1-{\frac {T+t}{T}}\cdot e^{-{\frac {t}{T}}}$

Verfahren zur Ermittlung der Modellregelstrecke:

Die Durchführung der Konstruktion des Modells kann grafisch in das aufgezeichnete Diagramm der Sprungantwort der unbekannten Regelstrecke erfolgen.

Wesentlich einfacher ist der Verlauf des PT2-Gliedes durch ein Simulationsprogramm zu gestalten, wenn die Originalfunktion durch eine geeignete Anzahl von Messpunkten in das Rechenprogramm eingetragen wird. Die Vorgehensweise für das grafische Verfahren und für die Anwendung eines Simulationsprogrammes ist in beiden Fällen identisch. Für die Konstruktion des Modells wird die Kennlinie des PT2-Gliedes im mittleren Amplitudenbereich des Originals durch schrittweises Ändern der beiden Zeitkonstanten T der Neigung des Kennlinienverlaufs des Originals angeglichen. Die Deckung der beiden Kennlinien wird durch horizontale Verschiebung der Kennlinie des PT2-Gliedes – bei Vorliegen eines Simulationsprogrammes durch ein Totzeitglied – auf die Kennlinie des Originals erreicht. Danach erfolgt der Feinabgleich mit der Zeitkonstanten T und der Verschiebezeit (Ttv). Bei Deckungsgleichheit der beiden Kennlinien können die Zeitkonstanten des Modells mit Ttv und T abgelesen werden.

Wenn die Totzeit der Originalstrecke nicht größer als 50 % der dominanten Zeitkonstante ist, kann mit den ermittelten Daten des Modells Ks, Ttv und T ein PID-Regler in Produktdarstellung optimal mit Führungseigenschaften parametriert werden nach folgenden Regeln:

Polstellen-Nullstellenkompensation: Tv1 = T, Tv2 = T,
Verstärkung: $K_{\mathrm {PID} }={\frac {0{,}6}{Ttv\cdot Ks}}$

Die Streckenverstärkung Ks ergibt sich aus dem Verhältnis von y / u der Originalstrecke im statischen Zustand.

Ergebnis: Die Sprungantwort des Regelkreises enthält ca. 5 % bis 10 % Überschwingungen mit dem Dämpfungsgrad D ca. > 0,5

Siehe unter Parametrierung eines PID-Reglers: „Beispiel: PID-Reglerstruktur für eine Regelstrecke mit zwei Verzögerungen und einer Totzeit“.

Die zugehörige Grafik zeigt die gute Deckung der Kennlinien der Sprungantworten des Modells und des Originals. Die gefundenen Parameter des Modells eignen sich gut für die Parametrierung eines PID-Reglers.

Fehlerbetrachtung der Sprungantwort des Modells zur Sprungantwort der Originalfunktion:

Für Strecken höherer Ordnung mit beliebigen Zeitkonstanten und Totzeit-Glied ist die Anwendung des vorgeschlagenen Modells bezogen auf die Sprungantworten der beiden Systeme relativ genau mit einem zu erwartenden Amplitudenfehler von 0,5 % bis 1 %. Lediglich bei einer nicht realistischen Regelstrecke, bei der z.B. vier ähnliche oder gleich große Zeitkonstanten auftreten, kann ein systembedingter Fehler – sorgfältige Anpassung der beiden Kennlinien vorausgesetzt – von 3 % auftreten. Der Fehler der Sprungantwort eines Regelkreises, der die Originalstrecke oder das Modell bei sonst gleichen Regler-Einstellungen enthält, ist natürlich größer.

Identifikation einer Regelstrecke mit Ausgleich und Totzeit durch die Impulsantwort (Gewichtsfunktion)

Die Impulsfunktion kann durch einen normierten Impuls definiert werden. Die Impulsbreite $\Delta t\,$ des Produktes $u\cdot \Delta t=1$ soll sehr klein sein gegenüber den Zeitkonstanten des Übertragungssystems. In der Praxis genügt ein Wert für $\Delta t\,$ von 1 % bis 10 % der dominanten Zeitkonstante des zu prüfenden Übertragungssystems. Die sich aus dieser Beziehung ergebene Amplitude von y ist auf mögliche Begrenzungseffekte des Übertragungssystems zu prüfen, andernfalls ergeben sich Fehler in der Impulsantwort.

Modell für eine Regelstrecke mit Hilfe der Impulsantwort

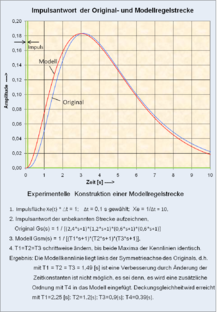
Impulsantwort einer Regelstrecke 4. Ordnung mit dominanter Zeitkonstante und deren Modellregelstrecke 3. Ordnung

Analog zum Modell-Beispiel mit der Sprungantwort wird ein Modell mit drei Verzögerungen mit folgender Übertragungsfunktion vorgeschlagen:

$G_{sm}(s)={\frac {1}{(T1\cdot s+1)\cdot (T2\cdot s+1)\cdot (T3\cdot s+1)}}$

Liegt eine Totzeit in der Originalfunktion vor, muss das Modell um ein Totzeitglied erweitert werden. Im Gegensatz zum Modell mit der Sprungantwort kann mit einem PT2-Glied und einem Totzeitglied keine Deckung der Kennlinien der Impulsantworten des Originals und des Modells erzielt werden, weil die Kennlinie der Impulsantwort empfindlicher auf Fehlanpassung reagiert.

Die experimentelle Parametrierung des Modells erfolgt schrittweise durch Verändern der Zeitkonstanten, wobei zuerst der Scheitelwert der Impulsantwort des Modells und dann die gesamte Kennlinie bei gleichem Scheitelwert mit der Kennlinie der unbekannten Impulsantwort zur Deckung gebracht wird.

Bei der Konstruktion der Kennlinien-Deckung bei gleichem Scheitelwert der Impulsantworten fällt auf:

Eine oder alle Zeitkonstanten des Modells müssen verkleinert werden, wenn die Kennlinie des Modells rechts der Symmetrieachse des Scheitelwertes des Originals liegt. Andernfalls ist die Ordnung des Modells höher als das Original.
Liegt die Kennlinie der Impulsantwort links der Symmetrieachse des Scheitelwertes des Originals, müsste eine zusätzliche Verzögerung in das Modell einbezogen werden, wenn man Deckungsgleichheit beider Kennlinien erzielen möchte.

Grafisch ist dieses Modell nur schwer zu erstellen. Es empfiehlt sich die Anwendung eines Simulationsprogramms für die drei PT1-Glieder.

Die zugehörige Grafik der Impulsantworten des Originals und des Modells zeigt keine vollständige Übereinstimmung der beiden Kennlinien, weil das Original Zeitverzögerungen 4. Ordnung enthält. Dennoch ist das ermittelte Modell mindestens so genau wie das ermittelte Modell mit der Sprungantwort.

Vergleich der Qualität der Modelle mit der Sprungantwort und der Impulsantwort

Die Impulsantwort eines Übertragungssystems ist identisch mit der Differentiation der Sprungantwort des Systems. Deshalb ist der mittlere Bereich um den Wendepunkt der Kennlinie der Sprungantwort durch die Differentiation stark vergrößert. Das Verfahren mit dem Vergleich der Kennlinien der Impulsantworten eines Streckenmodells und des Originals erlaubt eine genauere Identifikation der Strecke als mit dem Vergleich der Sprungantworten. Den Beweis kann man nur durch Simulation beider Verfahren in einem Regelkreis antreten.

Stabilität der Regelstreckenglieder

Wenn für ein Übertragungssystem alle Koeffizienten der Differentialgleichung von der höchsten Ableitung von $y^{(n)}(t)$ bis y(t) lückenlos vorhanden und positiv sind, dann ist zunächst eine Grundforderung der Stabilität des Systems erfüllt.

Ein lineares zeitinvariantes Übertragungssystem ist asymptotisch stabil (auch intern stabil genannt), wenn seine Impulsantwort (Gewichtsfunktion) nach genügend langer Zeit asymptotisch abklingt. Steigt dagegen die Impulsantwort nach genügend langer Zeit gegen eine natürliche Anschlagbegrenzung, ist das System instabil.

Als Sonderfall gibt es Systeme, die nach der Impulsantwort mit steigender Zeit zwar ansteigen, aber einen endlichen Grenzwert nicht übersteigen. Diese auch mit grenzstabil bezeichneten Systeme betreffen z.B. das I-Glied oder das T2-Schwingungsglied.

Interne Stabilität

Interne Stabilität bedeutet, dass jedes Glied der Regelstrecke stabil ist. Ein Übertragungssystem ist intern stabil, wenn die Übertragungsfunktion nur Pole in der linken s-Halbebene hat:

Externe Stabilität (BIBO-Stabilität)

Sie bezieht sich im Gegensatz zur internen Stabilität auf das Gesamtsystem des Regelkreises. Ein Übertragungssystem gilt als extern stabil, wenn ein beschränktes Eingangssignal an dem System auch ein beschränktes Ausgangssignal hervorruft. Dabei können einzelne Elemente des Regelkreises instabil sein, solange der gesamte Regelkreis stabiles Verhalten aufweist.

>Bedeutung der Pole und der konjugiert komplexen Polpaare in der linken und rechten s-Halbebene

Ein Regelstreckensystem ist instabil

wenn die Ausgangsgröße kontinuierlich schwingt,
wenn die Ausgangsgröße mit ansteigenden Amplituden schwingt,
wenn die Ausgangsgröße progressiv über alle Grenzen ansteigt.

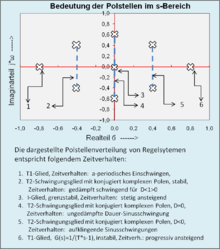
Stabilitätsbetrachtung durch Lage der Pole

Es genügt, für die Erkennung der Stabilität einer Übertragungsfunktion die Lage der Pole in der s-Ebene (Ordinate mit Ϭ, Abszisse mit j*ω) zu betrachten:

Asymptotische Stabilität: sämtliche Pole müssen in der linken s-Halbebene liegen,
Instabilität: wenn mindestens ein Pol in der rechten s-Halbebene liegt oder wenn ein mehrfacher Pol auf der Imaginären Achse der s-Ebene liegt.
Grenzstabil: wenn kein Pol in der rechten s-Halbebene liegt, keine mehrfachen Pole auf der imaginären Achse der s-Halbebene liegen und mindestens ein einfacher Pol vorhanden ist.

Regelstrecke im Zustandsraum

→ Hauptartikel: Zustandsraumdarstellung

siehe auch Regler#Zustandsregler

In der klassischen Regelungstheorie hatte die Analyse und Berechnung von Regeleinrichtungen im Zeitbereich nur eine geringere Bedeutung als die Methoden im Frequenz- und s-Bereich, wie die Laplace-Transformation, der Frequenzgang und das Wurzelortsverfahren. Dabei wurden hauptsächlich lineare zeitinvariante Übertragungsglieder mit konstanten Koeffizienten behandelt. Nichtlineare Systeme wurden linearisiert.

Erst mit dem Aufkommen von digitalen Rechnern war auch die Berechnung und Simulation von Regelkreisen mit numerischen Methoden möglich. Anstelle der Berechnung des kontinuierlichen Verhaltens der physikalischen Größen eines dynamischen Systems als f(t) erfolgt die Umsetzung in eine quantisierte Berechnungsmethode mit konstanten kleinen Zeitintervallen, der diskretisierten Zeit Δt. Das dynamische System wird mit Differenzengleichungen beschrieben und algebraisch berechnet.

Die seit den 1960er Jahren bekannte Theorie des Zustandsraumes stammt aus den USA von Rudolf E. Kalman. Sie kann die oben genannte klassische Regelungstheorie nicht ersetzen, wohl aber um einige Verfahren erweitern. Das Zustandsraummodell basiert auf den systemtheoretischen Begriff des Zustandes eines dynamischen Systems. Diese Modellform erlaubt viele Analyse- und Entwurfsverfahren der Regelungstechnik, wie z.B.:

Nichtlineare Systeme,
Systeme mit mehreren Eingangs- und Ausgangsgrößen,
Lineare Übertragungsglieder mit zeitabhängigen Koeffizienten (zeitvariable Systeme),
Synthese von optimalen Regelsystemen.

Das Modell beschreibt den Zusammenhang zwischen dem Eingangssignal u(t) und dem Ausgangssignal y(t) eines Übertragungssystems. Damit ist es möglich, für ein gegebenes Eingangssignal u(t) mittels der Modellbeschreibung das erzeugte Ausgangssignal y(t) zu berechnen.

Bei der Aufstellung der Modelle geht man von den physikalischen Grundgesetzen aus, wie z.B. bei elektrischen Systemen von den Kirchhoffschen Gesetzen, bei mechanischen Systemen von den Erhaltungssätzen für Energie und Impuls.

Bei den Modellen der Dynamik eines Übertragungssystems beschreiben die Inhalte der Systemspeicher den Zustand des Systems zu einem bestimmten Zeitpunkt. Aus der Kenntnis des Zustandes der Speicher zu einem beliebigen Zeitpunkt t = t(0), der als Anfangszustand x(t0) bezeichnet wird, und dem Verlauf der Eingangsgröße e(t), folgt das Verhalten des Modells für alle nachfolgende Zeiten.

Diese physikalischen Beziehungen werden mathematisch in eine Differenzialgleichung und dann in ein Zustandsraummodell umgesetzt. Ein alternativer Weg zur theoretischen Modellbildung ist die experimentelle Identifikation eines Übertragungssystems, bei dem das Modell anhand eines bekannten Eingangssignals e(t) an dem System über das Verhalten des Ausgangssignals identifiziert wird.

Der Zustand eines linearen dynamischen Systems mit n Energiespeichern wird durch n Zustandsgrößen oder Zustandsvariablen $x_{1}(t),\ x_{2}(t)\cdots x_{n}(t)\,$ beschrieben, die zu einem Zustandsvektor ${\underline {x}}(t)\,$ zusammengefasst werden. Die Zustandsgrößen beschreiben den inneren Bewegungsablauf des Systems. Bei Übertragungssystemen ohne differenzierende Anteile sind sie physikalisch die Energieträger des Systems. Bei einem Feder-Massesystem sind das z.B. die potentiellen und kinetischen Energieanteile.

Die Zustandsgrößen eines mathematischen Modells einer Regelstrecke mit konzentrierten Speichern (im Gegensatz zu verteilten Speichern) können aus einer gewöhnlichen systembeschreibenden Differentialgleichung bestimmt werden. Dabei werden die Terme der Ableitungen der Ausgangsgröße jeweils integriert und mit den zugehörigen Koeffizienten auf den Systemeingang zurückgeführt. Dies entspricht im Prinzip dem Signalflussplan der klassischen Lösung einer Differentialgleichung durch analoge Rechentechnik, wobei die Zustandsgrößen die Ausgänge der Integratoren sind.

Unter der Zustandsraumdarstellung versteht man die Beschreibung eines dynamischen Systems durch seine Zustandsgrößen. Dabei werden sämtliche Beziehungen der Zustandsgrößen, der Eingangsgrößen und Ausgangsgrößen in Form von Matrizen und Vektoren dargestellt.

Mathematisch geht es bei der Zustandsdifferenzialgleichung um die Umwandlung einer Differenzialgleichung n-ter Ordnung in n Differentialgleichungen 1. Ordnung.

Für die Regelungstechnik ist die Einbindung der Zustandsgrößen zu einem Zustandsregler anstelle der klassischen Ausgangsrückführung sehr vorteilhaft für die Dynamik des Regelkreises. Die Zustandsgrößen wirken zeitlich schneller als die Ausgangsrückführung eines Standardregelkreises. In erster Linie geht es bei der Behandlung von Regelsystemen im Zustandsraum um die Nutzung dieser dynamischen Eigenschaft.

Alle Zustandsgrößen einer Regelstrecke müssen für den Zustandsregler verfügbar sein. Sie können an der Regelstrecke gemessen werden, was aber häufig aus verschiedenen Gründen nicht möglich ist. Abhilfe bietet ein Zustandsbeobachter, der über ein mathematisches Modell der Regelstrecke die Zustandsvariablen für den Zustandsregler rekonstruiert.

Begriffsdefinition dynamischer Übertragungssysteme im Zustandsraum

Zustandsraum:

Ein dynamisches System im Zustandsraum wird durch seine inneren Systemgrößen, den Zustandsgrößen, beschrieben. Die Zustandsgrößen werden aus der systembeschreibenden Differentialgleichung eines Modells der Regelstrecke durch Integrationsverfahren aller Ableitungen der Ausgangsgröße ermittelt.

Der Zustand eines Systems mit n Energiespeichern ist durch n Zustandsgrößen $x_{1},x_{2}\cdots x_{n}\,$ bestimmt. Die Zustandsgrößen sind die inneren Systemgrößen, die das dynamische Übertragungsverhalten festlegen. Diese werden zu einem Zustandsvektor ${\underline {x}}\,$ zusammengefasst. Der Wert der Zustandsgrößen zu einem bestimmten Zeitpunkt t ist der Zustand des Systems. Physikalisch ist der Zustand eines Systems durch das Verhalten seiner Energiespeicher zu einem bestimmten Zeitpunkt durch die Anfangsbedingungen $x(t=0)=x(0)\,$ gegeben.

Die Anzahl der Zustandsgrößen des Zustandsvektors ${\underline {x}}(t)\,$ ist die Dimension des Zustandsraumes.

Zustandsraumdarstellung

Die Zustandsraumdarstellung wird definiert als die Verknüpfung der Eingangsgrößen, Ausgangsgrößen und Zustandsvariablen eines Übertragungssystems in Form von Matrizen und Vektoren.

Die Behandlung eines Systems im Zustandsraum ist nicht zwangsläufig an die Systembeschreibung in Form von Matrizen gebunden. Das zeitliche Verhalten der Ausgangsgröße y(t) und der Zustandsgrößen x(t) kann auch leicht mittels numerischer Methoden als Funktion eines beliebigen Eingangssignals w(t) berechnet und grafisch dargestellt werden.

Zustandsraummodell

Das Zustandsraummodell eines Übertragungssystems beschreibt symbolisch durch Matrizen und Vektoren die Regelungsnormalform. Es zeigt in einer standardisierten Form den Zusammenhang des Eingangssignals u(t), des Ausgangssignals y(t) und die additive Rückführung der Zustandsgrößen auf das Eingangssignal in Form von Matrizen und Vektoren. Es beschreibt Ein- und Mehrgrößensysteme.

Das Blockdiagramm des Zustandsraummodells ist ein vereinfachtes Modell, das die erste Ableitung des Zustandsvektors ${\underline {x}}'(t)\,$ und die einfache Integration des Zustandsvektors und dessen Rückführung anzeigt. Es symbolisiert die überführte Differentialgleichung n-ter Ordnung in n-gekoppelte Zustands-Differentialgleichungen erster Ordnung. Die tatsächlichen Signalflüsse und Zustandsgrößen, die sich aus der systembeschreibenden Differenzialgleichung höherer Ordnung ergeben, werden in dem Diagramm der Signalflüsse der Regelungsnormalform angezeigt.

Die dem System zugehörigen ebenfalls standardisierten Zustandsdifferentialgleichung und Ausgangsgleichung beschreiben vollständig das Übertragungssystem mit Matrizen und Vektoren.

Die Gleichungen der Ableitung des Zustandsvektors ${\underline {x}}'(t)\,$ und die Ausgangsvariable y(t) ergeben sich algebraisch anhand des Bockdiagramms des Zustandsraummodells.

Zustandsgrößen

Die Zustandsgrößen (= Zustandsvariablen) beschreiben physikalisch den Energiegehalt der in einem dynamischen System enthaltenen Speicherelemente. Sie können sich bei Anregung des Systems nicht sprunghaft ändern und bedeuten physikalisch z.B. Spannung an einem Kondensator, Strom in einer Induktivität, bei einem Feder-Massesystem die potentiellen und kinetischen Energieanteile.

Die meisten linearen Übertragungssysteme bzw. Regelstrecken höherer Ordnung lassen sich durch gewöhnliche Differentialgleichungen n-ter Ordnung beschreiben. Die Zustandsgrößen $x_{1}(t)\cdots x_{n}(t)\,$ ergeben sich aus der Differentialgleichung, indem alle Ableitungen der Ausgangsgröße y(t) integriert und mit dem zugehörigen Koeffizienten von der Eingangsgröße u(t) subtrahiert werden (= Addition negativer Koeffizienten der Pole des Übertragungssystems).

Systemmatrix

Die Systemmatrix ${\underline {A}}\,$ enthält die Koeffizienten der Zustandsgrößen. Durch die Regelungsnormalform kann die Systemmatrix nach einem relativ einfachen Schema erstellt werden. Die Koeffizienten eines Übertragungssystems n-ter Ordnung stehen in einer Zeile der Matrix.

Bei Mehrgrößensystemen mit verkoppelten Übertragungsgliedern können die Bestimmung der Zustandsvariablen und die Auslegung der Systemmatrix aufwendig werden. Für jede Ausgangsgröße $y_{1}(t)\cdots y_{n}(t)\,$ lässt sich eine verkoppelte Übertragungsfunktion bzw. die zugehörige Differenzialgleichung bestimmen. Daraus werden die Koeffizienten für die n*n-Systemmatrix ${\underline {A}}\,$ gebildet.

Durchgangsmatrix

Im Normalfall der Regelungstechnik gilt für die Beschreibung des Übertragungsverhaltens der Regelstrecke das Pole- Nullstellenverhältnis n > m, d.h. die Anzahl der Pole n ist größer als die der Nullstellen m des Systems. In diesem Fall ist das System nicht sprungfähig. Die Durchgangsmatrix ${\underline {D}}(t)\,$ beziehungsweise der Durchgangsfaktor ${d}(t)\,$ wird zu Null.

Normalformen im Zustandsraum für lineare Übertragungssysteme

Es existieren verschiedene Formen von Signalflussplänen, von denen die bekanntesten die Regelungsnormalform (auch mit Frobenius-Form, Steuerungsnormalform oder 1. Standardform bezeichnet) und die Beobachtungsnormalform sind.

In der Matrizen-Vektordarstellung der Zustandsgleichungen haben beide Normalformen ein festgelegtes Schema der Koeffizienten in der Systemmatrix ${\underline {A}}\,$ der systembeschreibenden Differenzialgleichung beziehungsweise der Übertragungsfunktion.

Die Regelungsnormalform zeigt die Umsetzung und Lösung der Differenzialgleichung in die physikalischen analogen Signalflüsse der Zustandsgrößen einschließlich der Ausgangsgröße bei gegebener Eingangsgröße. Man kann sie als eine Weiterentwicklung der in der Analogrechentechnik bekannten Verfahren zur Lösung einer Differentialgleichung n-ter Ordnung mit n Integratoren betrachten.

Sie ist besonders geeignet für Reglerentwurf, z.B. mit dem Polvorgabe-Verfahren. Von den n*n Elementen der Systemmatrix ${\underline {A}}\,$ ist nur die letzte Zeile vom Übertragungssystem abhängig.

Beobachtungsnormalform

Sie ist besonders geeignet zur Überprüfung der Systemeigenschaft auf die Beobachtbarkeit. Von den n*n Elementen der Systemmatrix ${\underline {A}}\,$ ist nur die letzte Spalte vom Übertragungssystem abhängig.

Steuerbarkeit und Beobachtbarkeit von Übertragungssystemen

Steuerbarkeit

Ein System ist steuerbar, wenn es von einem beliebigen Anfangszustand nach endlicher Zeit in einen beliebigen Endzustand gebracht werden kann.

Allgemein gilt auf die Signalgrößen bezogen:

Ein System ist vollständig zustandssteuerbar, wenn für jede Anfangszeit $t_{0}\,$ jeder Anfangszustand ${\underline {x}}_{0}(t)\,$ nach endlicher Zeit durch einen unbeschränkten Steuervektor ${\underline {u}}(t)\,$ in jeden beliebigen Endzustand ${\underline {x}}\,$ gebracht werden kann.

Beobachtbarkeit

Zustandsbeobachter können nur realisiert werden, wenn das zu beobachtende System beobachtbar ist, was bei den allermeisten technischen Regelstrecken der Fall ist.

Ein lineares Übertragungssystem ist beobachtbar, wenn durch Messung der Ausgangsvariablen y(t) der Anfangszustand des Zustandsvektors ${\underline {x}}_{0}\,$ nach endlicher Zeit bestimmt werden kann. Die Eingangsvariable u(t) muss bekannt sein.

Ein System heißt vollständig beobachtbar, wenn jeder Anfangszustand ${\underline {x}}(t_{0})\,$ aus den Messungen des Ausgangssignals y(t) in einem bestimmten Zeitintervall ab $t_{0}\,$ exakt bestimmt werden kann.

Blockdiagramm eines Zustandsraummodells eines Eingrößensystems

Bei der Zustandsraumdarstellung wird von einem Blockdiagramm der Signalflüsse eines Zustandsraummodells ausgegangen. Die gezeigte Darstellung bezieht sich auf ein Eingrößensystem, kann aber leicht auf ein Mehrgrößensystem erweitert werden.

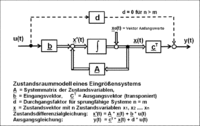
Symbolisches Blockdiagramm eines Modells eines Übertragungssystems 1. Ordnung in Zustandsraumdarstellung für ein Eingrößensystem.

Das Blockdiagramm des Zustandsraummodells zeigt symbolisch die Signalflüsse eines linearen Übertragungssystems n-ter Ordnung, das durch Umwandlung in n Differenzialgleichungen erster Ordnung überführt wurde. Es stellt den Zusammenhang der Ableitung des Zustandsvektors ${\underline {x}}'(t)\,$ mit der Systemmatrix ${\underline {A}}\,$ eines linearen Übertragungssystems mit den Eingangsgrößen ${\underline {u}}(t)\,$ und Ausgangsgrößen ${\underline {y}}(t)\,$ dar.

Die mathematische Beschreibung des Zustandsraummodells erfolgt durch die Zustandsdifferenzialgleichung und durch die Ausgangsgleichung. Beide zusammen werden als Zustandsraumgleichungen bezeichnet.

Das Blockdiagramm des Zustandsraummodells hat eine einheitliche Form, wird aber als Ein- oder Mehrgrößensystem unterschiedlich dargestellt. Bei dem Mehrgrößensystem treten anstelle der skalaren Ein- und Ausgangsgrößen u(t) und y(t) die Vektoren ${\underline {u}}(t)\,$ und ${\underline {y}}(t)\,$ . Die Signalflüsse von Matrizen und Vektoren werden in dem Blockschaltbild durch Doppellinien dargestellt.

Gleichungen des Zustandsraummodells laut des dargestellten grafischen Signalflussplanes:

Gleichung	Bei Eingrößensystemen	Bei Mehrgrößensystemen
Zustandsdifferenzialgleichung (auch Zustandsgleichung)	${\underline {x}}'(t)={\underline {A}}\cdot {\underline {x}}(t)+{\underline {b}}\cdot u(t)$	${\underline {x}}'(t)={\underline {A}}\cdot {\underline {x}}(t)+{\underline {B}}\cdot {\underline {u}}(t)$
Ausgangsgleichung	$y(t)={\underline {c}}^{T}\cdot {\underline {x}}(t)+d\cdot u(t)$ d = 0 für n > m	${\underline {y}}(t)={\underline {C}}\cdot {\underline {x}}(t)+{\underline {D}}\cdot {\underline {u}}(t)$ ${\underline {D}}\,$ = 0 für n > m

Bedeutung der Signale und Systemblöcke des Zustandsraummodells:

Bedeutung	Eingrößensystem	Mehrgrößensystem
Ableitung des Zustandsvektors	${\underline {x}}'(t)\,$	${\underline {x}}'(t)\,$
Zustandsvektor	${\underline {x}}(t)\,$	${\underline {x}}(t)\,$
Zustandsvariable	${x}(t)\,$	${x}(t)\,$
Vektor der Anfangsbedingungen	${\underline {x}}_{0}(t)\,$	${\underline {x}}_{0}(t)\,$
Eingangssignale	${u}(t)\,$ Eingangsvariable	${\underline {u}}(t)\,$ Eingangsvariablenvektor
Ausgangssignale	${y}(t)\,$ Ausgangsvariable	${\underline {y}}(t)\,$ Ausgangsvariablenvektor
Systemmatrix	${\underline {A}}(t)\,$
Eingangsmatrix	${\underline {b}}(t)\,$ Eingangsvektor	${\underline {B}}(t)\,$ Eingangsmatrix
Ausgangsmatrix	${\underline {c}}^{T}(t)\,$ Ausgangsvektor (transponiert)	${\underline {C}}(t)\,$ Ausgangsmatrix
Durchgangsmatrix	${d}(t)\,$ Durchgangsfaktor = Null für n > m	${\underline {D}}(t)\,$ Durchgangsmatrix = Null für n > m

Anmerkung: Die mit Vektoren bezeichneten Größen bedeuten jeweils eine Spalte oder eine Zeile einer Matrix.

Zustandsdifferenzialgleichung und Ausgangsgleichung des Zustandsraummodells in Matrix- Vektorschreibweise:

Eingrößensysteme haben nur eine Eingangsgröße u(t) und eine Ausgangsgröße y(t). Dabei gehen die Eingangsmatrizen ${\underline {B}}\,$ und Ausgangsmatrizen ${\underline {C}}\,$ in den Eingangsvektor ${\underline {b}}\,$ und Ausgangsvektor ${\underline {c}}\,$ über.

Zustandsdifferenzialgleichungen der Eingrößensysteme

${\begin{bmatrix}x'_{1}(t)\\x'_{2}(t)\\\vdots \\x'_{n}(t)\\\end{bmatrix}}=\underbrace {\begin{bmatrix}a_{11}&\dots &a_{1n}\\a_{21}&\dots &a_{2n}\\\vdots &\ddots &\vdots \\a_{n1}&\dots &a_{nn}\\\end{bmatrix}} _{\text{System-Matrix}}\ *\underbrace {\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\\vdots \\x_{n}(t)\\\end{bmatrix}} _{\text{Zustd.-Vektor}}+\underbrace {\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\\\end{bmatrix}} _{\text{Eingangs-Vektor}}*\underbrace {\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\\vdots \\u_{m}(t)\\\end{bmatrix}} _{\text{Eing. Gr.-Vektor}}$

Ausgangsgleichung der Eingrößensysteme:

${\begin{bmatrix}y(t)\\\end{bmatrix}}=\underbrace {\begin{bmatrix}c_{1}&\dots &c_{n}\\\end{bmatrix}} _{\text{Ausgangs-Vektor}}\ *\underbrace {\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\\vdots \\x_{n}(t)\\\end{bmatrix}} _{\text{Zustd.-Vektor}}+\underbrace {\begin{bmatrix}d\\\end{bmatrix}} _{\text{Durchg.-Faktor}}*\underbrace {\begin{bmatrix}u(t)\\\end{bmatrix}} _{\text{Eing.-Variable}}$

Unter der Zustandsraumdarstellung in der Regelungsnormalform versteht man eine einheitliche Form der Matrizendarstellung mit folgenden vorteilhaften Eigenschaften:

Die Zählerkoeffizienten der Übertragungsfunktion (Nullstellen) sind nur in dem Ausgangsvektor ${\underline {c}}^{T}(t)\,$ enthalten,
Die Nennerkoeffizienten der Übertragungsfunktion (Pole) sind nur in der Systemmatrix ${\underline {A}}\,$ enthalten,
Die Systemmatrix ${\underline {A}}\,$ hat eine spezielle Struktur. Von den n*n Elementen sind nur die n-Elemente der letzten Zeile vom Übertragungssystem abhängig,
Der Eingangsvektor ${\underline {b}}\,$ ist unabhängig von den Systemeigenschaften.

Für den weiteren, über den Hauptartikel Zustandsraumdarstellung hinausgehenden Informationsbedarf, muss auf die Fachliteratur hingewiesen werden.

Mehrgrößensysteme

Siehe auch Artikel: Regler#Regler für Mehrgrößensysteme!

Wenn Regelstrecken mehrere Ein- und Ausgangsgrößen aufweisen, bezeichnet man sie als Mehrgrößensysteme. Dabei wirken mehrere Eingangssignale der Strecke wechselseitig auf die Ausgangsgrößen und auch umgekehrt.

Beispiele für Mehrgrößensysteme findet man

In der Chemoindustrie, z.B. bei der Mischung von Flüssigkeiten verschiedener Temperaturen zu einer Solltemperatur und einer bestimmten Flüssigkeitsmenge
in der Flugtechnik u.a. bei Hubschraubern: Stellgrößen für die Bewegung sind die Anstellwinkel des Hauptrotors und des Heckrotors, Ausgangsgrößen sind z.B. die Flughöhe und der Gierwinkel.

Diese Systeme können z.B. durch einschleifige Regelsysteme nicht zufriedenstellend geregelt werden.

Zweigrößen-Regelstrecken

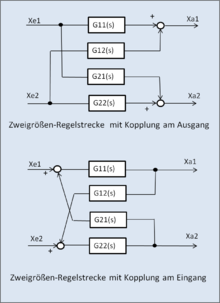
Darstellung einer Zweigrößen-Regelstrecke in zwei Beispielen, oben in P-kanonischer, unten in V-kanonischer Verkopplungs-Struktur

Von den bekanntesten Mehrgrößen-Regelstrecken ist die Struktur der Zweigrößen-Regelstrecken nachfolgend dargestellt.

Die Regelstrecke hat zwei Eingangsgrößen und zwei Ausgangsgrößen.
Beide Ausgangsgrößen sind dynamisch mit der jeweils anderen Eingangsgröße verkoppelt.
Je nach Vorzeichen der Additionsstellen unterscheidet man positive und negative Kopplung. Unter der negativen Kopplung versteht man bei Zweigrößen-Regelstrecken, dass nur eine von beiden Koppelstellen negativ eingreift.
Die Kopplung kann am Ausgang der Hauptstrecke wie auch am Eingang erfolgen.

Mehrgrößen-Regelsysteme können wie einschleifige Regelsysteme sowohl im Zeitbereich durch Differentialgleichungen, als Zustandsdarstellung und auch im Frequenzbereich durch Übertragungsfunktionen beschrieben werden.

Nach dem Blockschaltbild mit den Koppelstellen an den Ausgängen gelten für lineare Regelstrecken nach dem Überlagerungsprinzip mit

G11(s) und G22(s) als Hauptstrecken und
G12(s) und G21(s) als Koppelstrecken.

Die zugehörigen Übertragungsfunktionen der beiden Ausgangsgrößen für die Kopplung am Ausgang lauten:

$Y_{1}(s)=U_{1}(s)\cdot G11(s)+U_{2}(s)\cdot G12(s)$

$Y_{2}(s)=U_{2}(s)\cdot G22(s)+U_{1}(s)\cdot G21(s)\,$

Analog zu den Zweigrößen-Regelstrecken mit Kopplung am Ausgang gibt es die Zweigrößen-Regelstrecken mit der Kopplung am Eingang. Die zugehörigen Übertragungsfunktionen der beiden Ausgangsgrößen mit der Kopplung am Eingang lauten:

$Y_{1}(s)=(U_{1}(s)+U_{2}(s)\cdot G21(s))\cdot G11(s)\,$

$Y_{2}(s)=(U_{2}(s)+U_{1}(s)\cdot G12(s))\cdot G22(s)\,$

Darstellung einer Sprungantwort einer Zweigrößen-Regelstrecke mit negativer Kopplung am Ausgang

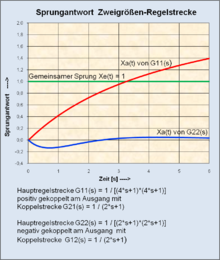
In der Grafik ist die Sprungantwort für eine Zweigrößen-Regelstrecke mit Kopplung am Ausgang dargestellt. Bei positiver Kopplung und Übertragungssystemen mit Ausgleich ohne Verstärkungsfaktoren ist die Ausgangsgröße im stationären Zustand immer y(t) = 2 * u(t). Bei negativer Kopplung ist die Ausgangsgröße unter den gleichen Bedingungen im stationären Zustand y(t) = 0. Vorübergehend kann y(t) je nach Verhalten der Koppelstrecke positive oder negative Werte annehmen.

Mehrgrößen-Regelkreise

Regelstrecken mit mehreren Eingangs- und Ausgangsgrößen werden ebenfalls von Reglern mit mehreren Eingangs- und Ausgangsgrößen geregelt. Liegen mehrere Regelgrößen vor, sind ebenfalls mehrere Sollwerte und Stellgrößen erforderlich, damit entsteht ein mehrschleifiger Regelkreis.

Die übliche Entwurfsstrategie von Reglern in einschleifigen Regelkreisen – z.B. Pol- Nullstellenkompensation – bringt bei Mehrgrößen-Regelsystemen keine zufriedenstellenden Resultate.

Abhilfe schafft die Methode, durch eine spezielle Struktur der Regler die Verkopplung zu eliminieren. Dafür sind bei den Zweigrößen-Regelkreisen vier Regler erforderlich, die einen Zweigrößen-Regelkreis in zwei einschleifige Regelkreise überführen können.

Andere Verfahren zur Vereinfachung von Mehrgrößensystemen sind „Modellreduktionen“ und „angenäherte Entkopplungen“. Siehe dazu auch Regler für Mehrgrößensysteme.-->

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de