Differenzengleichung

Differenzengleichungen werden zur numerischen Berechnung in vielen wissenschaftlichen Disziplinen – wie Wirtschaft, Medizin, Technik, Elektrotechnik, Kybernetik, Informatik, Akustik und andere – eingesetzt.

Eine Differenzengleichung ist eine numerisch lösbare Berechnungsvorschrift für eine diskret definierte Folge $k=[0,\ 1,\ 2,\ 3,\dotsc ]$ von Folgegleichungen, die Variablen $y_{(k)}$ zu fortlaufenden nummerierten Ereignissen bzw. nummerierten Zeitpunkten im Abstand eines Intervalls $\Delta x$ berechnen.

Die rekursive Lösung einer Differenzengleichung erster Ordnung erfolgt von einer Anfangsbedingung durch nummerierte Folgegleichungen, die sich je auf das Ergebnis einer zurückliegenden Folgegleichung bezieht. Bei Differenzengleichungen höherer Ordnung bezieht sich jede aktuelle Folgegleichung, entsprechend der Ordnungszahl, auf mehrere der zurückliegenden Folgegleichungen.

Das Lösungsergebnis $y_{(k)}=f(x_{(k)})$ besteht aus gestuften nummerierten Einzelergebnissen als sogenannte Funktions-Stützstellen (auch Knoten genannt).

Für die Aufstellung der meisten Differenzengleichungen werden verschiedene Verfahren eingesetzt, wie das einfache Euler-Streckenzugverfahren oder die besseren und aufwendigeren Mehrschrittverfahren. Die komplizierteren Mehrschrittverfahren benötigen vorteilhaft für ein gleiches genaues Berechnungsergebnis eine wesentlich geringere Anzahl von Folgegleichungen.

Zwischen einer Differentialgleichung und einer Differenzengleichung besteht eine enge mathematische Verwandtschaft. Wird der Differentialquotient durch einen Differenzenquotient ersetzt, entsteht die Differenzengleichung. Damit ist zwangsläufig ein Bezug zu einer zurückliegenden Folgegleichung gegeben.

Einfache Differenzengleichungen vom Typ $y_{(k+1)}=f(y_{(k)})$ mit nur einer Variablen $y_{(k)}$ und einer festen Stufung können auch ohne Differentialgleichungen durch logische Betrachtungsweisen entstehen (z.B. Bevölkerungswachstum, Zinseszins).

Der Schwerpunkt dieses Artikels befasst sich mit der Erstellung der Differenzengleichungen nach dem Euler-Streckenzug-Verfahren zur numerischen Berechnung dynamischer Systeme. Dabei werden auch andere Diskretisierungsverfahren, Totzeitsysteme, nichtlineare Systeme und die z-Transformation tangiert.

Anwendung numerische Berechnungsmethoden mit Differenzengleichungen

Numerische Berechnungen im wissenschaftlichen Bereich hoher Genauigkeit:

Für die numerische Berechnung wissenschaftlicher Aufgaben höchster Genauigkeit kommen meist (kommerzielle) Spezialprogramme zum Einsatz.

Anwendungen sind z.B. Wettersimulation oder Flugbahnverfolgung von Satelliten (Raumflugmechanik). Dabei werden häufig Großrechenanlagen eingesetzt.

Kommerzielle Programme numerischer Verfahren:

Für den ingenieurtechnischen Bereich stehen die bekanntesten Programme wie Matlab und Simulink mit umfangreichen Befehlssätzen für die theoretische Modellierung von dynamischen Systemen und vielen speziellen kybernetischen und regelungstechnischen Anwendungen zur Verfügung. Für diese Aufgaben ist ein normal ausgestatteter Personal Computer geeignet.

Kommerzielle Programme zur numerischen Berechnungen wie Matlab unterscheiden sich von einfachen numerischen Eulerverfahren in drei wesentlichen Punkten:

Es kann eine gewünschte Berechnungsgenauigkeit durch ausgewählte Verfahren bestimmt werden.
Die gewählten Verfahren sind adaptiv, d.h. es muss kein diskretes Intervall (auch Zeitintervall) und maximale Folge vorgegeben werden. Die Größe des Intervalls ist auch nicht über alle Folgen konstant.
Die gewählten Verfahren kontrollieren die Stabilität der Lösung.

Numerische Verfahren mit Differenzengleichungen:

Als einfachstes Verfahren zur Erstellung der Differenzengleichungen wird meistens das explizite Euler-Streckenzugverfahren verwendet.

Andere Methoden der numerischen Berechnung bedienen sich zur besseren Approximation z.B. an Stelle des Euler-Streckenzugverfahrens des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Adams-Bashforth-Verfahren) und anderer Verfahren. Grund der aufwendigeren Approximationsverfahren und damit der umfangreicheren Differenzengleichungen ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Mikrocomputern und dessen Schnittstellen bei Echtzeitberechnungen erforderlich sein kann.

Offline-Anwendung zur numerischen Simulation dynamischer Systeme:

In vielen Anwendungsfällen werden Differenzengleichungen offline als Computer-Simulation am Personal Computer zur zeitdiskreten Darstellung dynamischer Vorgänge verwendet. Hierbei ist die diskretisierte Zeit $\Delta t$ ein Parameter, keine echte Zeit.

Bei dynamischen Übertragungssystemen G(s)

beliebiger Ordnung interessiert das zeitliche Verhalten des Ausgangssignals y(t)

als Funktion des Eingangssignals u(t)

und der Systemparameter.

Jede Differenzengleichung einer Programmzeile ist eine Folgegleichung mit der Ausgangsgröße $y_{(k)}$ und bezieht sich entsprechend dem Rekursions-Algorithmus bei Differenzengleichungen 1. Ordnung auf eine zurückliegende Zeile $y_{(k-1)}$

Das Ergebnis ist eine gespeicherte Tabelle von Programmzeilen mit den Berechnungsfolgen $k=(0,1,2,3,\dotsc ,k_{\mathrm {max} })$ gegeben. Die Ausgangsgröße $y_{(k)}$ der Endgleichung einer Zeile liegt im Abstand $\Delta t$ vor und kann leicht zu einer Grafik f(t)

gestaltet werden.

Online-Anwendung der digitalen Regelung:

Bei der digitalen Regelung erfolgt im einfachsten Falle eine zeitliche Abtastung und Digitalisierung der Regeldifferenz. Im gleichen Abtast-Intervall berechnet ein Mikrocomputer mit Hilfe von Differenzengleichungen den notwendigen Regel-Algorithmus. Die digitale Ausgangsgröße des Reglers, die Stellgröße, wird für die meist analog wirkenden Regelstrecken durch Wandler analogisiert.

Bei solchen Signalabtastungen im Rhythmus der Abtastzeit T_A handelt es sich um eine echte Zeit.

Anders als bei der Simulation muss der Mikrocomputer kontinuierlich unendlich oft im Abstand der Abtastzeit für jede neue Eingangsgröße einen neuen Digitalwert berechnen.

Bei den häufig vorkommenden Differenzengleichungen 1. Ordnung wird nur eine Programmeile für die Berechnung der aktuellen Ausgangsgröße $y_{(k)}$ und die Programmzeile $y_{(k-1)}$ der vorherigen Berechnung gespeichert. Jede Ausgangsgröße bezieht sich rekursiv auf die vorhergehende Ausgangsgröße als Eingangsgröße. Die Ergebnisse weiterer vorhergehender Programmzeilen werden nicht benötigt und deshalb gelöscht.

Eine Programmzeile beinhaltet je nach gewünschtem Regelalgorithmus mehrere Differenzengleichungen vorteilhaft in Produktdarstellung, weil differenziell wirkende Übertragungsglieder des Reglers die verzögernd wirkenden Übertragungsglieder der Regelstrecke kompensieren können. Damit wird die Parametrierung des Digitalreglers sehr vereinfacht, indem die Zeitkonstanten der differenzierenden Komponenten des Reglers denen der Verzögerungsglieder der Regelstrecke gleichgesetzt werden.

Die Ausgangsgröße einer Differenzengleichung ist die Eingangsgröße der nächsten Differenzengleichung der gleichen Programmzeile.

In der Fachliteratur unterscheiden sich Differenzengleichungen je nach der Aufgabenstellung, dem Diskretisierungsverfahren, der Art der physikalischen Größen und den dargestellten Größenbezeichnungen erheblich.

Grundlagen der Differenzengleichungen

Zum besseren Verständnis dieses Themas werden Kenntnisse der Differentialrechnung, der Laplace-Transformation und der s-Übertragungsfunktion vorausgesetzt.

Differentialgleichungen

Eine lineare Differentialgleichung enthält die gesuchte Funktion y=f(x) und deren Ableitungen nur in der ersten Potenz. Es dürfen auch keine Produkte der gesuchten Funktion und ihren Ableitungen auftreten. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen.

Eine Differentialgleichung, in der gewöhnliche Ableitungen einer unbekannten Funktion y(x) bis zur n-ten Ordnung auftreten, wird als gewöhnliche DGL n-ter Ordnung bezeichnet. Die zu den Ableitungen zugehörigen Koeffizienten können variabel sein oder konstante Zahlenwerte enthalten. Sind es Konstanten, bezeichnet man diese Differentialgleichungen als gewöhnliche lineare Differentialgleichungen mit konstanten Koeffizienten. Lineare gewöhnliche Differentialgleichungen mit konstanten Koeffizienten werden gerne als Spezialform bezeichnet, dennoch kommt dieser Typ Differenzialgleichung in der Systemtheorie und Regelungstechnik hauptsächlich zur Anwendung.

Lösung einer Differentialgleichung:

Unter einer Lösung der Differentialgleichung $y'=f[x,y(x)]$ versteht man eine Funktion $y=y(x)$ , keinen Einzelwert.

Die Lösung einer Differentialgleichung erfolgt durch Integration. Die Integration ist keine eindeutige Rechenoperation, denn man erhält zu jeder Funktion f(x) verschiedene Stammfunktionen F(x) mit dem Begriff des unbestimmten Integrals.

Bei der Integration wird zwischen dem bestimmten und dem unbestimmten Integral unterschieden. Die Stammfunktion F(x) ist Lösung des unbestimmten Integrals:

Lösung der Differentialgleichung: $y'=f(x)$

$y=\int f(x)dx=F(x)+C$

Diese Lösung ist unbestimmt wegen der unbestimmten Integrationskonstante . Jede Integration ergibt Integrationskonstanten, deren Anzahl durch die Ordnung der Differentialgleichung bestimmt ist. Die Lösung einer Differentialgleichung n-ter Ordnung enthält voneinander unabhängige Integrationskonstanten. Diese sind für eine spezielle Lösung der Differentialgleichung abhängig von den Eigenwerten und gegebenen Anfangsbedingungen des Übertragungssystems zu bestimmen.

Nichtlineare Differentialgleichungen sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Sie können mittels der numerischen zeitdiskreten Methoden gelöst werden.

Differenzengleichungen aus Differentialgleichungen

Die kontinuierlichen mathematischen Operationen der Integration und Differentiation der Differentialgleichungen werden bei Differenzengleichungen diskret durch Summen- und Differenzenbildung angenähert.

Differenzengleichungen beziehen sich allgemein auf die Differentialquotienten einer Differentialgleichung, die durch Differenzenquotienten $\Delta y/\Delta x$ (Differenzenquotient 1. Ordnung) ersetzt werden. Damit entsteht eine numerisch lösbare rekursive Differenzengleichung in Annäherung an die analytische Lösung der Differentialgleichung [rekursiv = Mathematik: zu bekannten Werten zurückgehend].

Definitionen der Parameter:

Nachfolgend wird die unabhängige Variable mit und die abhängige Variable mit oder oder bezeichnet. Handelt es sich um Zeitvorgänge, so wird als unabhängige Variable und oder als abhängige Variable bezeichnet.
Die Größe ist die übliche Bezeichnung einer mathematischen Folge von Daten. Andere Bezeichnungen einer Folge innerhalb der Fachliteratur sind "" und "".
Die Größe ist das Intervall (Schrittweite) zwischen den Folgen mit der unabhängigen Variablen . Bei Zeitvorgängen ist das Intervall $\Delta t$ .
Die Indizierung der diskreten Größen wie:

$y_{(k)}$ = "Aktuelle Größe"; $y_{(k+1)}$ = "um einen positiven Folgeschritt geänderte aktuelle Größe"; $y_{(k-1)}$ = "um einen Schritt zurückliegende Größe".

Homogene und inhomogene Differenzengleichung:

Aus der Differentialgleichung $y'=f[x,y(x)]$ entsteht die diskrete Differenzengleichung $y_{(k+1)}=f\,[y_{(k)},x_{(k)},\Delta x]$ . Die Indizierung der Differenzengleichung mit der Folge kennzeichnet, dass es sich um eine schrittweise Annäherung an die analytische Funktion der Lösung $y=y(x)$ handelt.

Die Lösung einer Differenzengleichung bezieht sich meist auf die Integrationsgrenzen der Wertefolgen von $y_{(k=0)}$ bis $y_{(k=kmax)}$ . Deshalb existiert das Problem der Integrationskonstanten der numerischen Berechnung nicht.

Aus der allgemeinen Form einer homogenen linearen Differentialgleichung erster Ordnung mit den konstanten Koeffizienten und entsteht durch Austausch des Differentialquotienten durch einen Differenzenquotienten ${\frac {y_{(k+1)}-y_{(k)}}{h}}$ und der Schrittweite die rekursive Differenzengleichung:

$y'+a\cdot y(x)=0\qquad \to \qquad y_{(k+1)}+h\cdot a\cdot y_{(k)}=0$

Bedeutung: Ein dynamisches System mit einer zu Null gesetzten Differenzengleichung startet von einem Anfangswert $y_{(0)}>0$ . Die Systembewegung $y_{(k)}$ ist sich selbst mit dem momentanen Inhalt seines Systemspeichers überlassen.

Aus der allgemeinen Form einer inhomogenen linearen Differentialgleichung erster Ordnung entsteht durch Austausch des Differentialquotienten durch einen Differenzenquotienten ${\frac {y_{(k+1)}-y_{(k)}}{h}}$ und der Schrittweite die rekursive Differenzengleichung:

$y'+a\cdot y(x)=b\cdot u(x)\qquad \to \qquad y_{(k+1)}+h\cdot a\cdot y_{(k)}=b\cdot u_{(k)}$

Bedeutung: Ein dynamisches System mit einer Eingangsgröße $u_{(k)}$ startet von einem Anfangswert $y_{(0)}\geq 0$ . Der Verlauf der Ausgangsgröße $y_{(k)}$ ist abhängig von der Eingangsgröße und dem Verhalten seines Systemspeichers.

Dynamische Systeme werden durch verschiedene Formen von Differentialgleichungen beschrieben.

Lösung einer Differenzengleichung:

Die Lösung einer linearen Differenzengleichung in Annäherung an die analytische Funktion $y(x)=f(x)$ ist eine Folge von nummerierten Folgegleichungen der Folge $k=[0,1,2,3,\dotsc ]$ im Abstand $\Delta x$ .

Nichtlineare Übertragungssysteme können – durch Separieren der Nichtlinearität (z.B. Hammerstein-Modell) – häufig mit Hilfe von logischen Operatoren wie z.B. mit WENN-DANN-SONST-Anweisungen bei Signalbegrenzungen und Hysterese gelöst werden. Auch für System-Totzeitverhalten existieren numerische INDEX-Anweisungen durch rückwertige Tabellen-Spaltenverschiebungen.

Differenzengleichungen nach dem Euler-Streckenzugverfahren

Euler Streckenzugverfahren:

Allgemein berechnen Differenzengleichungen in Annäherung an eine kontinuierliche Funktion y=f(x) schrittweise eine Wertefolge $y_{(k)}$ mit den Folgegliedern $k=[0,1,2,3,\dotsc ]$ für ein kleines Intervall $h=\Delta x$ die Wertefolge $y_{(k)}=y_{(0)},y_{(1)},y_{(2)},y_{(3)},\dotsc$ an der Stelle $x_{(k)}=x_{(0)},x_{(1)},x_{(2)},x_{(3)},\dotsc$ , wobei eine Nummerierung der errechneten Werte $y_{(k)}$ darstellt.

Ist eine Funktion y(x) mit einem Anfangswert $y(x_{0})=y_{0}$ für eine Differentialgleichung 1. Ordnung gegeben, lässt sich über die Differenzengleichung in Annäherung an die analytische Funktion die nächste Stützstelle $y_{(k+1)}$ an der Stelle $x_{(k+1)}$ für die Schrittweite $h=\Delta x$ berechnen. Das gilt auch für alle weiteren Stützstellen im Abstand , die sich schrittweise der analytischen Funktion annähern. In der Praxis muss zur grafischen Darstellung des kontinuierlichen Funktionsverlaufs y=f(x) nicht interpoliert werden, PC-Grafikprogramme beherrschen die Interpolation der Stützstellen.

Die Differenzengleichung verknüpft je nach Größe der Ordnung die aktuell errechneten Werte der Stützstellen zu einer oder zu mehreren zurückliegenden Stützstellen.

$y_{(k)}=f[y_{(k-1)},y_{(k-2)},y_{(k-3)},\dotsc ]$

Zum leichteren Verständnis des Euler-Streckenzug-Verfahrens werden Differenzengleichungen 1. Ordnung mit einer Ableitung betrachtet. Jede gewöhnliche Differentialgleichung höherer Ordnung lässt sich in einzelne Differentialgleichungen 1. Ordnung überführen. Ein zusammenhängendes Übertragungssystem in Form von Differenzengleichungen 1. Ordnung lässt sich hintereinander für jede Folge und einer gegebenen Eingangsgröße berechnen. Dabei ist jeder errechneter Ausgangs-Folgewert die Eingangsgröße der nächsten Differenzengleichung der gleichen Folge. Berechnete Übertragungssysteme mit mehreren Differenzengleichungen und einer endlichen Folge von k=0 bis $k_{\mathrm {max} }$ werden im PC zur besseren Übersicht tabellarisch gespeichert. Jede Zeile mit den Differenzengleichungen ist mathematisch identisch und zeigt von links nach rechts das jeweilige Teilergebnis der entsprechenden Folge.

Lineare Übertragungssysteme höherer Ordnung, die in Differentialgleichungen 1. Ordnung zerlegt werden und deren Systemverhalten mittels Differenzengleichungen 1. Ordnung berechnet werden, konvergieren nach dem Euler-Verfahren zur analytischen Funktion, wenn das Intervall beziehungsweise im Zeitbereich das Intervall $\Delta t$ gegen Null geht.

Explizites Euler-Streckenzugverfahren (Euler-Vorwärts)

Darstellung der Integrationsschritte des expliziten Euler-Streckenzugverfahrens.

Das klassische Verfahren der Lösung von Differentialgleichungen mit Differenzengleichungen ist das explizite Euler-Verfahren mit der Berechnungsfolge .

Das Verfahren wird für jeden Rechenschritt (Stützpunkt, Knoten) $y_{(k)},x_{(k)}$ für die Ableitung y'(x) durch einen Vorwärts-Differenzenquotienten approximiert. Der Begriff Vorwärts-Differenzenquotient bezieht sich auf die linke Intervallgrenze laut Diagramm $x_{(0)}$ nach $x_{{(1)}}$ mit dem Intervall .

Der Vorwärts-Differenzenquotient für eine Funktion y'=f(x,y) lautet:

$y'\approx {\frac {\Delta y}{\Delta x}}={\frac {y(x+h)-y(x)}{(x+h)-x}}:={\frac {y_{(k+1)}-y_{(k)}}{h}}$

Beim Euler-Vorwärts-Verfahren wird das Integral für einen Streckenzug approximiert:

$\int _{x}^{x+h}f[y(x)dx]\approx h\cdot f[y_{k},x_{k}]$

Die Annäherung für das Integral ist die Festlegung, dass der Integrand f(x,y) im gesamten Integrationsintervall konstant ist und durch den Wert f(x,y) am linken Rand des Integrationsintervalls ersetzt werden kann. $x_{0}$ und $y_{0}$ sind bekannte Größen (Anfangswerte).

Der Algorithmus zur Approximation des Integrals führt auf folgende Berechnungsvorschrift:

Explizite Form der Differenzengleichung der Vorwärtsdifferenz:

$y_{(k+1)}=y_{(k)}+h\cdot f(y_{(k)},x_{(k)})$

Für die Terme der Differenzengleichung lassen sich die Integrationsgrenzen der Indizierungen um (−1) zurücksetzen. Damit entsteht eine identisch verwendbare Form der Differenzengleichung als Rückwärtsdifferenz (siehe Implizites Eulerverfahren):

$\underbrace {y_{(k)}} =\underbrace {y_{(k-1)}} +\ \underbrace {h\cdot f(y_{(k-1)},x_{(k-1)})}$

Dabei bedeutet:

${y_{(k)}}$ = ${\begin{bmatrix}y_{(0)}&=&0&+&\ h\cdot f(y_{(0)},x_{(0)})\\y_{(1)}&=&y_{(0)}&+&\ h\cdot f(y_{(1)},x_{(1)})\\y_{(2)}&=&y_{(1)}&+&\ h\cdot f(y_{(2)},x_{(2)})\\y_{(k)}&=&y_{(k-1)}&+&\ h\cdot f(y_{(k)},x_{(k)})\\\end{bmatrix}}$

${y_{(k)}}$ sind die aktuellen Lösungen der rekursiven Differenzengleichung. ${y_{(k=0)}}$ ist der Folge k=0

zugeordnet.

$y_{(k-1)}$ = das um einen Schritt zurückliegende Ergebnis,
${h\cdot f(y_{(k-1)},x_{(k-1)})}$ bedeutet: Parameter der diskretisierten Differentialgleichung zu einer Differenzengleichung.

Diese Parameter und sind in jeder Berechnungsfolge konstant. (Es existieren aber auch aufwendigere Diskretisierungsverfahren, die variable Intervalle benutzen.)

Durch die Anwendung dieser Form der Differenzengleichung (Rückwärtsdifferenz) ergibt sich der Verlauf von ${y_{(k)}}$ als Obersumme gegenüber der analytischen Funktion y=f(x) . Die zugehörige Differenzengleichung entsteht erst durch Einsetzen des Differenzenquotienten anstelle des Differenzialquotienten in der Differentialgleichung.

Das explizite Eulerverfahren wird auch unter dem Begriff: Integrationsformel (Euler-Cauchy-Verfahren) bezeichnet.

Implizites Euler-Streckenzugverfahren (Euler Rückwärts)

Darstellung der Tangenten der Euler-Streckenzugverfahren.

Bei diesem Verfahren wird nicht der – wie beim expliziten Verfahren berechnete Stützpunkt $y(x+h),(x+h)$ – benutzt, sondern ein neuer Punkt $y(x-h),(x-h)$ festgelegt. Das implizite Eulerverfahren entsteht, wenn bei der Approximation des Integrals durch eine Rechteckfläche mit der Höhe des Funktionswertes nicht am linken, sondern am rechten Rand des Intervalls festgelegt und als Stützpunkt verwendet wird.

Da dieser Stützpunkt zunächst unbekannt ist, besteht die Notwendigkeit, erst eine meist nichtlineare Gleichung (bzw. System) zu lösen. Diese kann mit geeigneten numerischen Verfahren, z.B. dem Newton-Verfahren, Fixpunktiteration gelöst werden. Dieses implizite Euler-Verfahren gilt als unbeschränkt stabil, d.h. der Größe des Intervalls unterliegt aufgrund der Stabilität keiner Beschränkung.

Das implizite Euler-Verfahren wird für jeden Rechenschritt (Stützpunkt, Knoten) $y_{(k)},x_{(k)}$ für die Ableitung y'(x) durch einen Rückwärts-Differenzenquotienten approximiert.

Der Rückwärts-Differenzenquotient für eine Funktion y'=f(x,y) lautet:

$y'\approx {\frac {\Delta y}{\Delta x}}={\frac {y(x)-y(x-h)}{(x+h)-x}}:={\frac {y_{(k)}-y_{(k-1)}}{h}}$

Beim Euler-Rückwärts-Verfahren wird das Integral für einen Streckenzug approximiert:

$\int _{x}^{x+h}f[y(x)dx]\approx h\cdot f[y_{k+1},x_{k+1}]$

Der Algorithmus zur Approximation des Integrals führt auf folgende Berechnungsvorschrift:

Implizite Form der Differenzengleichung der Rückwärtsdifferenz:

$y_{(k+1)}=y_{(k)}+h\cdot f(y_{(k+1)},x_{(k+1)})$

Anmerkungen:

Verfahren, bei denen zu jedem Stützpunkt eine Gleichung gelöst werden muss, werden als implizite Verfahren bezeichnet.

Beim implizierten Euler-Verfahren hängt $y_{(k+1)}$ von sich selbst ab. Zur Berechnung von $y_{(k+1)}$ ist meist die Lösung einer nichtlinearen Gleichung erforderlich.

Die nichtlineare Gleichung kann z.B. mit dem Newton-Verfahren gelöst werden.
Das implizierte Euler-Streckenzug-Verfahren gilt bei großen Schrittweiten (sind praktisch unbrauchbar) gegenüber dem expliziten Verfahren als das stabilere Verfahren. Die Approximation an die analytische Funktion ist bei beiden Methoden ähnlich.

Berechnungsbeispiel Euler-Streckenzugverfahren

Sind durch die numerische Berechnung einer Differentialgleichung die an die Originalfunktion approximierten Stützstellen ermittelt, können diese durch Interpolation, z.B. mit geraden Strecken als geschlossene Funktion dargestellt werden. Die Grafikfunktionen der Tabellenkalkulation stellen bei Tabellenwerten automatisch durch Interpolation geschlossenen Funktionen dar.

Entscheidend für das Ergebnis der numerischen Berechnung ist die Differenzengleichung in der Startzeile für x=0 , $y_{(k=0)}$ bzw. $y_{(k=1)}$ . Damit ist festgelegt, ob es sich bei dem Ergebnis $y_{(k)}$ um eine Obersumme oder Untersumme gegenüber der analytischen Funktion handelt. Ober- und Untersumme können sich durch eine einzelne Schrittweite unterscheiden.

Beispiel einer numerischen Berechnung einer gegebenen Differentialgleichung 1. Ordnung

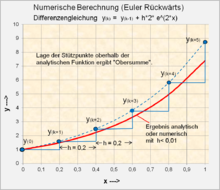
Numerische Berechnung einer Differentialgleichung mit Anfangswert.

Gegeben: Differentialgleichung $y'=2\cdot e^{2\cdot x}$ , Anfangswert $y_{0}=1$

Analytische Lösung: $y=e^{2\cdot x}$

Gesucht: Differenzengleichung nach Euler-Rückwärts:

Die Ableitung $y'={\frac {dy}{dx}}$
wird näherungsweise durch den Differenzenquotient ${\frac {y_{(k)}-y_{(k-1)}}{h}}$ ersetzt.

$y'=2\cdot e^{2\cdot x}\approx {\frac {y_{(k)}-y_{(k-1)}}{h}}=2\cdot e^{2\cdot x_{k}}$

Die Differenzengleichung wird nach $y_{(k)}$ freigestellt:

$y_{(k)}=y_{(k-1)}+h\cdot 2\cdot e^{2\cdot x_{k}}$

Schrittweite h = 0,2; e = 2,718.

Folge k	$x_{(k)}$	$y_{(k-1)}$	Parameter $h\cdot 2\cdot e^{2\cdot x_{k}}$	Ergebnis $y_{(k)}$	Analytisch $y(x)=e^{2\cdot x_{k}}$
0	0	0	0,4	$y_{{(0)}}$ = 1	1
1	0,2	1	0,597	1,597	1,492
2	0,4	1,597	0,890	2,487	2,225
3	0,6	2,487	1,328	3,815	3,320
4	0,8	3,815	1,981	5,796	4,952
5	1,0	5,796	2,955	8,751	7,387

Anmerkung zur Programmierung von Differenzengleichungen:

Das tabellarische Ergebnis $y_{(k)}=[y_{(0)},y_{(1)},y_{(2)},y_{(3)},\dotsc ,y_{\mathrm {(max)} }]$ ist eine Folge von Berechnungspunkten (Stützstellen) in Annäherung an die analytische Funktion. Werden diese Punkte interpoliert, entsteht eine geschlossene Funktion. Mit fallender Größe von konvergiert die numerische Lösung gegenüber der analytischen Funktion im Unendlichen.

Differenzengleichungen können mit jeder Programmiersprache berechnet werden. Da das Ergebnis der Berechnungsfolgen immer tabellarisch ist, empfiehlt es sich die Software der Tabellenkalkulation anzuwenden. Die Differenzengleichung wird beliebig oft kopiert. Der Vorteil: Das Programm macht keine Fehler, die Rechengenauigkeit (Dezimalstellen) ist sehr hoch, die grafische Darstellung der Funktion $y_{(k)}=f(x_{(k)})$ ist als XY-Diagramm bereits im Programm enthalten und muss nur aufgerufen werden.

Zur Erzielung einer höheren Genauigkeit der Approximation an die Originalfunktion sind viele Berechnungsfolgen, z.B. 100, 1000 und mehr, mit dem Euler-Streckenzug-Verfahren erforderlich, wenn ein Annäherungsfehler – bezogen auf den Endwert – von ca. 1 % zugelassen werden soll. Die Anzahl der Berechnungsfolgen kann abhängig von der gewünschten Auflösung von ${x_{(k=0)}}$ bis ${x_{(k=k_{\mathrm {max} })}}$ festgelegt werden. Die Grenzen der Genauigkeit bei Steigerung der Folgen sind gegeben, wenn die Rundungsfehler einer jeden Folge sich zu größeren Fehlerwerten aufaddieren können.

Bei einer Schrittweite von $h=0{,}01$ ergibt sich bei dem Rechenbeispiel für $y_{(k=100)}\to x_{(k=100)}=1$ ein Wert von 7,452 mit der Abweichung von 0,065. Dies entspricht einem Fehler von 0,88 %.
Bei einer Schrittweite von $h=0{,}001$ ergibt sich bei dem Rechenbeispiel für $y_{(k=1000)}\to x_{(k=1000)}=1$ ein Wert von 7,394 mit der Abweichung von 0,0065. Dies entspricht einem Fehler von 0,088 %.

Anmerkung zum Anfangswert: (Anfangswertproblem)
Wäre der Anfangswert $y_{0}=1$ nicht bekannt gewesen, dann würde die Differenzengleichung mit $y_{0}=0$ starten. Da diese Form der Differenzengleichung die Obersumme (die Approximation liegt oberhalb der analytischen Funktion) darstellt, ergäbe sich ein Wert für $y_{0}=0{,}4$ an der Stelle $x_{0}=0$ und damit eine Verschiebung aller anderen Werte für $y_{(k)}$ . Bei einem kleinen Folge-Endwert wäre damit ohne Kenntnis des Anfangswertes $y_{{(0)}}$ die Approximation falsch.

Mit dem Newton-Verfahren als Standard-Verfahren zur numerischen Lösung von nichtlinearen Gleichungen lassen sich Näherungswerte zu Lösungen der Gleichung f(x)=0 , d.h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d.h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt.

Der Vorteil der Darstellung der Obersumme ist die Differenzierbarkeit des Wertes y_0>0 an der Stelle $x_{0}=0$ . (Anwendung in der Systemtheorie und Regelungstechnik bei Stoßfunktionen).

Modifiziertes Eulerverfahren

Zur besseren Approximation an eine analytische Funktion besteht die Möglichkeit, anstelle der Vorwärts- oder Rückwärtsdifferenz den Mittelwert der beiden Gleichungen zu verwenden.

$y'\approx {\frac {\Delta y}{\Delta x}}={\frac {y{(x+h)}-y{(x-h)}}{2\cdot h}}$

Diese Gleichung wird als zentraler Differenzenquotient oder als symmetrische Differenz bezeichnet und entspricht dem Mittelwert aus der Vorwärts- und Rückwärtsdifferenz. Wird dieser Differenzenquotient in eine lineare Differentialgleichung eingesetzt, wird eine sehr gute Annäherung – auf Kosten eines höheren Berechnungsaufwandes – an die analytische Funktion erreicht.

Einfache Differenzengleichungen mit einer Variablen vom Typ $y_{(k+1)}=f(y_{(k)})$

Eine Differenzengleichung ist eine diskrete Berechnungsvorschrift für die Glieder einer rekursiv definierten Folge. Sie enthält Werte einer Variablen $y_{(k)}$ zu verschiedenen Zeitpunkten. Aus einem Element der Folge wird das nächste Folgeglied errechnet. Für die Berechnung der Folgeglieder wird immer ein Anfangswert $y_{(k)}=y_{(0)}$ benötigt, anderenfalls entsteht eine Vielzahl von Lösungen.

Es handelt sich hier bei diesem Abschnitt nicht um eine Approximation an einen Verlauf einer durch Differentialgleichungen vorgegebenen mathematischen Funktion, sondern die nachfolgend dargestellten Differenzengleichungen ergeben sich durch die Aufgabenstellung. Dabei wird bei den Folgegliedern unterschieden:

Bei der arithmetischen Folge wächst oder fällt jedes Folgeglied um einen festen Betrag.

Die allgemeine Form einer homogenen linearen Differenzengleichung 1. Ordnung lautet:

$y_{(k+1)}\pm h\cdot a\cdot y_{(k)}=0;\quad \mid \quad {\text{mit h = Zeitschritt, a = Konstante.}}$

Dabei ist eine Konstante. Die Schrittweite ist eine konstante Zeitdifferenz zwischen den Folgegliedern. Diese Berechnung mit einer arithmetischen Folge ist sehr einfach. Beispiel: Mit einer Spardose wird monatlich ein konstanter Betrag angespart. Zinsen gibt es dafür nicht.

Bei der exponentiellen Folge wächst oder fällt jedes Folgeglied um einen relativen Anteil.

Beispiel: Gegeben sei eine homogene Differenzengleichung folgender Schreibweise:

$\Delta y_{(k)}-0{,}5\cdot y_{(k)}=0\quad |\quad {\text{mit}}\quad \Delta y_{(k)}=y_{(k+1)}-y_{(k)}$

Diese Gleichung kann nach Gleichungsumstellungen in verschiedenen Formen gleichwertig dargestellt werden:

$y_{(k+1)}-y_{(k)}-0{,}5\cdot y_{(k)}=0\quad |\quad \Delta y_{(k)}=y_{(k+1)}-y_{(k)}\ {\text{eingesetzt}}$
$y_{(k+1)}-1{,}5\cdot y_{(k)}=0$
$y_{(k+1)}=1{,}5\cdot y_{(k)}$

Diese Form der Differenzengleichungen wird gerne für einfache Aufgabenstellungen wie Zinseszinsberechnung, zeitliche Entwicklung der Bevölkerungszahl, gebremstes Wachstum, Aufwärmen oder Abkühlen von Flüssigkeiten, Entleerung von Behältern (mit und ohne Reibung) und andere verwendet. Die Berechnung dieser Aufgaben ist exakt und kann durch Berechnung der einzelnen Folgeglieder tabellarisch für die Folge $k=[0,\ 1,\ 2,\ 3,\dotsc ]$ durchgeführt werden.

Für die exponentielle Folge kann eine Gleichung mit dem sogenannten Wachstumsfaktor als Basis für eine exponentielle Funktion erstellt werden, der die Berechnung einzelner Folgen $y_{(k)}$ für ein beliebiges erlaubt.

Beispiel der Berechnung einer Folge:

Aus der nachfolgenden Differenzengleichung 1. Ordnung werden die Folgegleichungen bestimmt:

$y_{(k+1)}=1{,}5\cdot y_{(k)}$ .

Folgegleichungen mit dem Anfangswert $y_{(0)}=4$ :

$y_{(0)}=4$

$y_{(1)}=1{,}5\cdot y_{(0)}=1{,}5\cdot 4=6$

$y_{(2)}=1{,}5\cdot y_{(1)}=1{,}5\cdot 6=9$

$y_{(3)}=1{,}5\cdot y_{(2)}=1{,}5\cdot 9=13{,}5$

Die Differenz $y_{(k+1)}-y_{(k)}$ der errechneten Folgeglieder ist nicht konstant. Die Werte der Folgeglieder $y_{(k)}$ nehmen einen exponentiellen Verlauf. Die Berechnung weiterer Folgeglieder kann in dieser Weise für beliebige Werte von tabellarisch erfolgen.

Aus dieser einfachen Differenzengleichung mit Hilfe der Folgeglieder $y_{(1)}=1,5\cdot y_{(0)}$ und $y_{(2)}=1{,}5\cdot y_{(1)}$ lässt sich das Bildungsgesetz für ein beliebiges nummeriertes Folgeglied erraten und bilden. Damit gilt für diesen Anwendungsfall der Faktor vor $y_{(k)}=1{,}5$ als Basis der Exponentialfunktion und wird als Wachstumsfaktor bezeichnet.

$y_{(k)}=1{,}5^{k}\cdot y_{(0)}$

Beispiel einer Differenzengleichung zur numerischen Berechnung des Bevölkerungswachstums

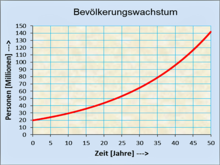
Beispiel des Bevölkerungswachstums über 50 Jahre in Abhängigkeit von der Geburtenrate und der Sterberate.

Gegeben:

Stand der Bevölkerung eines Staates am Jahresanfang: $B_{(0)}=20$ Millionen.
Konstante Geburtenrate nach Jahresende pro Jahr: $G=6$ %

Vernachlässigung: in den Anfangsjahren der neuen Geburtenjahrgänge sind keine Nachkommen möglich.

Konstante Sterberate nach Jahresende pro Jahr: $S=2$ %
Die Schrittweite beträgt Jahr
Gesucht: Entwicklung der Bevölkerung nach 50 Jahren.

Gesucht:

Differenzengleichung zur Bestimmung des Bevölkerungswachstums,
Tabellarische Bildung der Folgegleichungen,
Stand der Bevölkerung nach 50 Jahren,
Wachstumsfaktor.

Form der Differenzengleichung:

$B_{(k+1)}=B_{(k)}+B_{(k)}\cdot a\cdot h$

Anfangswert $B_{(0)}=20$ [Millionen] im Jahr Null mit $h_{(0)}=0$ ,

Bereinigte Geburtenrate $a=G-S=6-2=4$ [%].

Die tabellarische Entwicklung der Folgeglieder pro Zeiteinheit lautet:

Jahr k	Bevölkerung $B_{(k)}$ [Millionen]	$B_{(k)}+B_{(k)}\cdot 0,04\cdot h$	$B_{(k+1)}$ [Millionen]
0	20	$20+20\cdot 0{,}04\cdot 0=$	20
1	20	$20+20\cdot 0{,}04\cdot 1=$	$20{,}8$
2	$20{,}8$	$20{,}8+20{,}8\cdot 0{,}04\cdot 1=$	$21{,}632$
3	$21{,}632$	$21{,}632+21{,}632\cdot 0,04\cdot 1=$	$22{,}49728$
$\vdots$	$\vdots$	$\vdots$	$\vdots$
50	$B_{(49)}=(1{,}04)^{49}\cdot 20=136{,}667$	$B_{(k+1)}=B_{(50)}=(1{,}04)^{50}\cdot 20=$	$142{,}13366$

$B_{(k+1)}-B_{(k)}=B_{(k)}\cdot a\cdot h=1{,}04\cdot B_{(k)}$ . $\quad 1{,}04$ ist hier der Wachstumsfaktor.

Die Ergebnisse der Folgegleichungen ergeben Stützstellen mit potenziellem Wachstum.

Anmerkung: Ein mit dieser linearen Differenzengleichung berechnetes ungebremstes Wachstum wird es in der Praxis nicht geben, weil andere Einflüsse wie z.B. Nahrungsmittelknappheit dagegen wirken.

Beispiel einer numerischen Berechnung der Kapitalentwicklung mit Zinseszins

Modell: Differenzengleichungen vom Typ $y_{(k+1)}=f(y_{(k)})$ .

Bei der Zinseszinsberechnung handelt es sich um eine konstante Zunahme der jährlichen Zinsen bezogen auf den jeweiligen aktuellen angesparten Betrag einer Folge. Die Kapitalentwicklung vom Anfangskapital über die kommenden Jahre nimmt einen progressiven Verlauf.

Gegeben: Anfangswert = Kapital $K_{0}$ = 1000 €; Zins: = 2 % pro Jahr am Jahresende,
Laufzeit = 20 Jahre, Schrittweite = 1 Jahr.

Gesucht:

Differenzengleichung,
Tabellarische Bildung der Folgeglieder,
Endkapital,
Wachstumsfaktor.

Differenzengleichung aufgestellt:

$y_{(k+1)}=y_{(k)}+y_{(k)}\cdot p\cdot h$

Wachstumsfaktor: $y_{(k+1)}=y_{(k)}\cdot (1+p/100)=1{,}02\cdot y_{(k)}$

Aktuelle Formelzeichen eingesetzt:

$K_{(k+1)}=K_{(k)}+K_{(k)}\cdot p\cdot h\qquad {\text{Der Anfangswert von}}\ K_{(k)}=K_{(0)}=1000$ €.

Die tabellarische Entwicklung der Folgeglieder pro Zeiteinheit lautet:

Jahr h	Kapital [€] $y_{(k)}$	$y_{(k)}+y_{(k)}\cdot p\cdot h$	Kapital [€] $y_{(k+1)}$
0	1000	1000 + 1000 * 0,02 * 0 =	1000
1	1000	1000 + 1000 * 0,02 * 1 =	1020
2	1020	1020 + 1020 * 0,02 * 1 =	1040,40
3	1040,40	1020 + 1040 * 0,02 * 1 =	1061,208
$\vdots$	$\vdots$	$\vdots$	$\vdots$
19	1428,2462	1428,2462 * 0,02 * 1 =	1456,8112
20	1456,8112	1456,8112 * 0,02 * 1 =	1485,9474

Zum Vergleich, die Zinseszinsformel mit dem Zinssatz p und Anzahl n=20 (Jahre) der Zeiträume lautet:

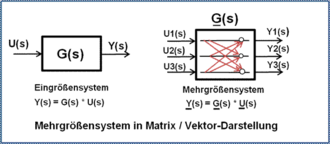
$K_{n}=K_{0}\left(1+{\frac {p}{100}}\right)^{n}=1000\cdot (1+0{,}02)^{20}=1485{,}9474$ €.

Differenzengleichungen für lineare Übertragungssysteme als Funktion der kontinuierlichen Beziehung $y(t)=f[u(t),t]$

Bei linearen Übertragungssystemen, die durch eine gewöhnliche Differentialgleichung mit konstanten Koeffizienten beschrieben werden, ergibt sich über die Anwendung der Laplace-Transformation eine Übertragungsfunktion G(s). Durch Ermittlung der Nullstellen im Zähler und Nenner der Übertragungsfunktion lässt sich über die Polynomdarstellung eine Faktorendarstellung erreichen. Durch die inverse Laplace-Transformation ergeben sich mit Hilfe des Laplace-Differentiationssatzes Differentialgleichungen 1. und 2. Ordnung als phasenminimale Elementarsysteme. Je nach Ordnung der gewöhnlichen Differentialgleichung existieren nur sechs phasenminimale unterschiedliche Elementarsysteme, die einfach oder mehrfach vorkommen kennen.

Aus den Elementarsystemen 1. und 2. Ordnung G(s) lassen sich über die zugehörigen Differentialgleichungen Differenzengleichungen entwickeln.

Grundlagen der linearen dynamischen Übertragungssysteme

Definition dynamisches System: Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Das System kann beispielsweise ein mechanisches Gebilde, ein elektrisches Netzwerk aber auch ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein. Es hat mindestens einen Signaleingang und einen Signalausgang.

Dynamische Systeme werden mit Hilfe mathematischer Werkzeuge als Modelle eines realen Übertragungssystems beschrieben. Damit lässt sich für gegebene Eingangssignale der Verlauf der Ausgangssignale von einem bestimmten Zeitpunkt $t=0=t_{(0)}$ für $t>t_{(0)}$ bestimmen. Ebenso eignen sich die Modelle zur Systemanalyse.

Übertragungsfunktion

eines linearen dynamischen Ein- und Mehrgrößensystems.

Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen. Systembeispiele: Feder-Masse-Dämpfungssystem, Elektrischer Schwingkreis.

Das Ausgangs- Eingangsverhalten technische Systeme können sich zeitabhängig, zeitunabhängig, linear, nichtlinear, kontinuierlich, diskontinuierlich, zeitinvariant, zeitvariant und totzeitbehaftet verhalten. Zu deren Berechnung müssen verschiedene Methoden der linearen und nichtlinearen numerischen Berechnung kombiniert werden.

Ferner können die internen Energiespeicher Anfangswerte enthalten, wenn das Signalverhalten eines Systems zu einem bestimmten Zeitpunkt $t_{0}$ innerhalb eines Einschwingvorgangs für t>0 betrachtete werden sollen.

In der linearen Systemtheorie ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen $G(s)$ von Übertragungsgliedern auf 6 Grundformen (ohne Totzeit) geschrieben bzw. zurückgeführt werden können. Diese Übertragungsglieder wurden aus einer gewöhnlichen Differentialgleichung höherer Ordnung mittels Laplace-Transformation bestimmt und haben integrierendes, differenzierendes und asymptotisches zeitverzögerndes Verhalten.

Übertragungsfunktionen der Verzögerungssysteme mit konjugiert komplexen Polen im Nennerpolynom lassen sich algebraisch nicht aufspalten und sind damit Systeme 2. Ordnung.

Systeme mit konjugiert komplexen Polen im Zählerpolynom der Übertragungsfunktion, d.h. differenzierendes Verhalten 2. Ordnung, haben in der Filtertechnik eine Bedeutung.

Dieses System $PD2_{kk}$ -Glied:

$G_{PD2}(s)=K_{PD2}\cdot (T^{2}s^{2}+2DTs+1)$ ist nicht in der Tabelle aufgeführt.

Ein in der Systemtheorie häufig auftretendes Übertragungssystem ist das Totzeitsystem $T_{t}$ . Es ist kein lineares System, es kann aber numerisch leicht behandelt werden.

Damit bestehen praktisch nur die 5 tabellarisch aufgeführten zeitabhängigen Systeme (ohne Totzeit) einfach oder mehrfach, die in der Praxis auftreten können. Sogenannte nichtreguläre Systeme (Nichtphasenminimum-Systeme) sind instabile Systeme. Auch sie können numerisch behandelt werden.

Tabelle wichtiger regulärer (phasenminimaler) Übertragungsfunktionen in Zeitkonstanten-Darstellung:

Übertragungsfunktion G(s) =		${\frac {1}{T\cdot s}}$	$T\cdot s$	$K_{PD1}(T\cdot s+1)$	${\frac {K_{PT1}}{T\cdot s+1}}$	${\frac {K_{PT2}}{T^{2}s^{2}+2DTs+1}}$	$K_{T_{t}}\cdot e^{-T_{t}\cdot s}$
Sprungantwort (Übergangsfunktion)
Benennung	P-Glied	I-Glied	D-Glied	PD₁-Glied	PT₁-Glied	PT₂-Glied	Totzeitglied

Durch die inverse Laplace-Transformation von Übertragungsfunktionen 1. Ordnung G(s) entstehen gewöhnliche Differentialgleichungen 1. Ordnung, die im nachfolgenden Abschnitt in Differenzengleichungen überführt werden. Das dargestellte Totzeitglied ist kein phasenminimales Übertragungsglied.

Eulerverfahren für Differenzengleichungen linearer und nichtlinearer Übertragungssysteme

Im technischen Bereich der Ingenieurwissenschaften beschreiben Differenzengleichungen zeitdiskret das spezifische Zeitverhalten linearer Übertragungssysteme für ein kleines Zeitintervall $\Delta t$ die Signaländerungen des Systemausgangs $y(k,\Delta t)$ (vereinfachte Schreibweise $y_{(k)}$ ) als Funktion des betreffenden kontinuierlichen Teilsystems (Linearfaktoren) G(s) in Abhängigkeit der Systemparameter und des Eingangssignals u(t) .

Das einfachste numerische Verfahren der Berechnung des Ausgangssignals y(t) eines linearen Übertragungssystems als Funktion des Eingangssignals u(t) ist das sogenannte explizite Eulerverfahren (auch Euler-Vorwärtsverfahren, Streckenzugverfahren, Rechteckverfahren, Tangentenverfahren genannt), bei dem durch wiederholte Berechnungen für ein kleines Zeitintervall $\Delta t$ eine Annäherung an die analytische Funktion des Systems durchgeführt wird.

Die numerische Integration einer monoton steigenden analytischen Funktion für ein Zeitintervall entspricht der Fläche des berechneten Ausgangssignals $y_{(k)}$ einer beliebigen Folge für die Zeit $\Delta t$ , also $y_{(k)}\cdot \Delta t$ . Je nach verwendetem Verfahren der numerischen Annäherung an die rechte oder linke Intervallgrenze der Folge $k-1,k,k+1$ spricht man von der Annäherung als Obersumme oder Untersumme der Integration.

Die Funktion einer einfachen Integration wird durch die Summe der Folgen des Produktes $u_{(k)}\cdot \Delta t$ nachgebildet:

$y(t)={\frac {1}{T_{I}}}\cdot \int u(t)\cdot dt\quad \rightarrow \quad y_{(k)}={\frac {1}{T_{I}}}\cdot \sum _{k}u_{(k\cdot \Delta t)}\cdot \Delta t$

Differenzengleichungen für eine endliche Folge $k=[0,1,2,3,\dotsc ,k_{\mathrm {(max)} }]$ berechnen die Integrationsgrenzen eines bestimmten Integrals, nämlich k=0 bis $k=k_{\mathrm {max} }$ .

Differenzengleichungen entstehen durch Einsatz eines Differenzenquotienten anstelle des Differentialquotienten der Differentialgleichung, die das System beschreibt. Durch fortlaufende Berechnung ausgehend vom Stützpunkt mit dem Anfangswert $[y_{(0)},t_{(0)}]$ und Berechnung des nächsten Stützpunktes $[y_{(1)},t_{(1)}]$ durch $f[System(t),t,u(t)]$ ergibt sich durch Interpolation der Stützstellen ein geschlossener Funktionsverlauf für die Stützpunkte $[y_{(k=0)}{\text{ bis }}y_{(k=max)}]$ im Abstand $\Delta t$ in Annäherung an den analytischen Verlauf des Übertragungssystems. Zur grafischen Darstellung des Funktionsverlaufs y=f(t) wird die Interpolation der Stützstellen selten benötigt.

Differenzengleichungen für lineare Systeme
Die numerische Gesamtlösung des Systemverhaltens erfolgt rekursiv über viele Berechnungsfolgen $k=[0;1;2;3;\dotsc ;k_{\mathrm {(max)} }]$ in je kleinen meist konstanten Zeitintervallen als Stützstellen in Annäherung an die analytische Funktion.

Jede aktuelle Berechnungsfolge (bei Euler-Rückwärts) $y_{(k)}$ bezieht sich bei Differenzengleichungen 1. Ordnung auf das vorhergehende Ergebnis $y_{(k-1)}$ und addiert die Änderung des Eingangssignals u_(k) unter Berücksichtigung der Systemübertragungsfunktion und des Zeitintervalls $\Delta t$ .

Lineare Übertragungssysteme höherer Ordnung werden pro Folge hintereinander durch die systembeschreibenden Differenzengleichungen 1. Ordnung für $k=[0;1;2;3;\dotsc ;k_{\mathrm {(max)} }]$ pro Zeile in tabellarischer Darstellung berechnet. Dabei wird in jeder Folge (Zeile) pro Teilsystem 1. Ordnung die Ausgangsgröße $y_{(k)}$ zu einer Eingangsgröße $u_{(k)}$ des nächsten Teilsystems, vorausgesetzt, es handelt sich um eine Reihenschaltung der Teilsysteme. Diese Anordnung der Differenzengleichungen kann auch mit Totzeitsystemen und nichtlinearen Systemen kombiniert werden.

Das Ergebnis ist eine tabellarisch im Rechner gespeicherte Folge von Berechnungswerten (Stützstellen) mehrerer Systeme 1. Ordnung im zeitlichen Abstand $\Delta t$ pro Zeile. Die Werte der Stützstellen mehrerer Teilsysteme lassen sich in Abhängigkeit von dem Eingangssignal $u_{(k)}$ und der diskreten Zeit grafisch für die Teilsysteme und des Gesamtsystems darstellen.

Die numerische Berechnung erlaubt tabellarisch und grafisch eine völlige Durchsicht des inneren Bewegungsablaufs dynamischer Übertragungssysteme.

Die Genauigkeit der numerischen Berechnung eines dynamischen Systems mit dem Euler-Verfahren steigt linear mit dem kleiner werdenden Zeitintervall $\Delta t$ . Die Genauigkeit wird begrenzt durch steigende Folgen $k_{\mathrm {max} }$ mit steigenden Rundungsfehlern.

Instabile nicht phasenminimale Übertragungssysteme

Die Ausgangssignale solcher Übertragungssysteme streben monoton einem unendlich hohen Wert an. Diese Übertragungssysteme 1. Ordnung werden umgangssprachlich – sachlich nicht korrekt – auch als instabile $PT1$ -Glieder benannt. Diese instabilen nicht phasenminimalen elementare Übertragungsfunktionen enthalten ein negatives Zeichen in der Übertragungsfunktion G(s) und in der zugehörigen Differenzengleichung. Nicht phasenminimale Übertragungsglieder 2. Ordnung als instabile $PT2_{{kk}}$ Glieder streben oszillierend mit einer bis ins Unendliche steigenden Amplitude an. Die Übertragungsfunktion G(s) enthält ebenfalls ein Minuszeichen und in der zugehörigen Differenzengleichung.

Nichtlineare Systeme

Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Mit handelsüblichen Personal-Computern kann das Verhalten beliebig vermaschter Systemstrukturen mittels numerischer Berechnung relativ einfach ausgeführt werden. Dabei sind für die Anwendung von Differenzengleichungen relativ geringe mathematische Kenntnisse erforderlich.

Treten bei linearen Übertragungssystemen G(s) zusätzlich Begrenzungseffekte, nichtlineares Verhalten oder Totzeitverhalten auf, kann das zeitliche Verhalten des Systems nur numerisch mit der diskreten Zeit $\Delta t$ berechnet werden. Alternativ können mit selbst erstellten beliebigen Rechenprogrammen des einfachen Euler-Verfahrens mit Differenzengleichungen in Kombination mit logischen Operatoren sehr effiziente Simulationen dynamischer Systeme mit nichtlinearen Elementen durchgeführt werden.

Ist einer Übertragungsfunktion G(s) die transzendente Funktion des Totzeitgliedes $e^{-s\cdot T_{t}}$ multiplikativ angehängt, dann kann das Gesamtsystem nicht mehr algebraisch behandelt werden. [transzendent (Mathematik): über das algebraische hinausgehend].

Für Totzeitsysteme existiert in der Tabellenkalkulation ein Befehl unter dem Oberbegriff "Nachschlagen und verweisen"

$INDEX\,[Bezug,\ Zeile,\ Spalte,\ Bereich]$ (z.B. $INDEX(F20;F200;180-T_{t}/\Delta t$ ),

der in einer Spalte einen Bezug zu einer bereits zurückliegenden Zelle macht. Die Totzeit $T_{t}$ muss nur in Folgewerte $y(k\cdot \Delta t)$ zugeordnet werden.

Nichtlineare Systeme ohne Zeitverhalten sind je nach Funktion Unikate, für die selten kommerzielle Programme zur Verfügung stehen. Handelt es sich um unstetige Funktionen (z.B. Signale die die Zustände $EIN$ oder $AUS$ annehmen), können diese mit logischen Funktionen mit sogenannten $WENN,\ DANN,\ SONST\ -Anweisungen$ definiert werden.

Signalbegrenzungen (z.B. mechanische Anschläge) verhalten sich ebenfalls nichtlinear. Auch sie können mit den genannten logischen Funktionen berechnet werden.

Für nichtlineare stetige Funktionen müssen notfalls eigene Tabellenwerte berechnet werden.

Die nachfolgende Berechnung und Aufstellung der Differenzengleichungen gilt für alle phasenminimalen 4 Formen der Übertragungssysteme 1. Ordnung. Diese linearen Systeme kommen einfach und mehrfach in größeren technischen Anlagen vor. Das $PT2_{{kk}}$ -Schwingungsglied lässt sich einfach über einen Hilfsregelkreis mit einem I-Glied und PT1-Glied nachbilden (Siehe Abschnitt "Differenzengleichungen höherer Ordnung").

Differenzengleichung der Integration (I-Glied)

Die Übertragungsfunktion lautet:

$\ G(s)={\frac {Y(s)}{U(s)}}={\frac 1{T_{I}\cdot s}}$

Die zugehörige Differenzialgleichung lautet:

$T_{I}\cdot {\dot y}(t)=u(t)$

Der Differenzenquotient wird an Stelle des Differenzialquotienten ${\dot y}(t)$ eingesetzt:

$T_{I}\cdot {\frac {y_{{(k)}}-y_{{(k-1)}}}{\Delta t}}=u_{{(k)}}$

Damit lautet die nach $y_{(k)}$ umgestellte Differenzengleichung des I-Gliedes:

$y_{{(k)}}=y_{{(k-1)}}+u_{{(k)}}\cdot {\frac {\Delta t}{T_{I}}}$

Differenzengleichung des Differenzierers (ideales D-Glied)

Mit der Zeitdiskretisierung wird der Übergang einer Differenzialgleichung in eine Differenzengleichung von einer zeitkontinuierlichen Systembeschreibung in eine Systembeschreibung mit kleinen Zeitintervallen Δt der diskreten Zeit geschaffen. Der Differentialquotient wird durch einen Differenzenquotient ersetzt.

Die Übertragungsfunktion des idealen Differenzierers lautet:

$G(s)={\frac {Y(s)}{U(s)}}=T_{V}\cdot s$

Differenzialgleichung des idealen Differenzierers:

$y(t)=T_{V}\cdot {\frac {d}{dt}}{u(t)}$

Der Differenzialquotient ${\dot {u}}(t)$ wird durch einen Differenzenquotient mit der Anpassung an die linke Intervallgrenze ersetzt. Für eine Anpassung an die rechte Intervallgrenze steht der Wert u_(k+1) nicht zur Verfügung.

${\dot {u}}(t)={\frac {du}{dt}}\approx {\frac {\Delta u}{\Delta t}}={\frac {u_{(k)}-u_{(k-1)}}{\Delta t}}$

Differenzengleichung der Differentiation (Ideales D-Glied)

$y_{{(k)}}=(u_{{(k)}}-u_{{(k-1)}})\cdot {\frac {T_{V}}{\Delta t}}$

Differenzengleichung der Verzögerung (PT1-Glied)

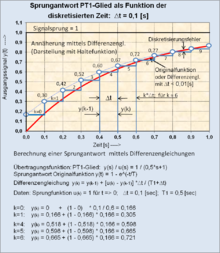
Rechteck-Approximation eines PT1-Gliedes durch Berechnung mit einer Differenzengleichung.

Übertragungsfunktion des PT1-Gliedes: $G(s)={\frac {Y(s)}{U(s)}}={\frac {K_{{PT}}}{1+s\cdot T_{1}}}={\frac {{\frac {K_{{PT}}}{T_{1}}}}{s+{\frac 1{T_{1}}}}}$

Zugehörige Differenzialgleichung: ${\dot y}(t)+{\frac 1{T_{1}}}\cdot y(t)={\frac {K_{{PT}}}{T_{1}}}\cdot u(t)$

Der Differenzialquotient der Differenzialgleichung wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:

${\frac {y_{{(k)}}-y_{{(k-1)}}}{\Delta t}}+{\frac 1{T_{1}}}\cdot y_{{(k)}}={\frac {K_{{PT}}}{T_{1}}}\cdot u_{{(k)}}$

Diese Gleichung wird nach y_(k) aufgelöst.

$y_{{(k)}}+{\frac {\Delta t}{T_{1}}}\cdot y_{{(k)}}=y_{{(k-1)}}+{\frac {K_{{PT}}\cdot \Delta t}{T_{1}}}\cdot u_{{(k)}}$

Die Differenzengleichung des PT1-Gliedes lautet:

$y_{{(k)}}={\frac {T_{1}}{T_{1}+\Delta t}}\cdot y_{{(k-1)}}+{\frac {\Delta t\cdot K_{{PT}}}{T_{1}+\Delta t}}\cdot u_{{(k)}}$

Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:

$y_{{(k)}}=y_{{(k-1)}}+(K_{{PT}}\cdot u_{{(k)}}-y_{{(k-1)}})\cdot {\frac {\Delta t}{T_{1}+\Delta t}}$

Differenzengleichung der Proportional-Differenzialfunktion (Ideales PD1-Glied)

Übertragungsfunktion PD1-Glied:

$G(s)={\frac {Y(s)}{U(s)}}=K_{{PD}}\cdot (T_{V}\cdot s+1)$

Die zugehörige Differenzialgleichung lautet:

$y(t)=K_{{PD}}\cdot T_{V}\cdot {\dot u}(t)+K_{{PD}}\cdot u(t)$

Der Differenzialquotient der Differenzialgleichung wird ersetzt durch den Differenzialalgorithmus mit folgendem Ansatz:

$y_{{(k)}}=K_{{PD}}\cdot T_{V}\cdot {\frac {u_{{(k)}}-u_{{(k-1)}}}{\Delta t}}+K_{{PD}}\cdot u_{{(k)}}$

Die Differenzengleichung des idealen PD1-Gliedes lautet:

$y_{{(k)}}=K_{{PD}}\cdot [u_{{(k)}}+(u_{{(k)}}-u_{{(k-1)}})\cdot {\frac {T_{V}}{\Delta t}}]$

Anmerkung: Differenzierende Systeme ohne sogenannte parasitäre Zeitkonstanten von PT1-Gliedern lassen sich als Hardware technisch nicht herstellen. Die parasitäre Zeitkonstante ist wesentlich kleiner, als die Zeitkonstante des Differenzierers. Dennoch kann man numerisch mit idealen Differenzierern rechnen, dabei ist die Größe des Impulses der Sprungantwort umgekehrt proportional der Größe von Δt. Erst bei der energetischen Bereitstellung als Stellgröße in einem Regelkreis ergibt sich durch die nachgeschaltete Hardware eine unvermeidbare Zeitverzögerung.

Tabelle der Differenzengleichungen (Euler-Rückwärts) der Elementarsysteme G(s) erster Ordnung

Elementarsysteme	P-Glied	I-Glied	D-Glied	PD₁-Glied	PT₁-Glied
Übertragungsfunktion	${\frac {Y}{U}}(s)=K$	${\frac {Y}{U}}(s)={\frac {1}{T\cdot s}}$	${\frac {Y}{U}}(s)=T\cdot s$	${\frac {Y}{U}}(s)=K\cdot (T\cdot s+1)$	${\frac {Y}{U}}(s)={\frac {K}{T\cdot s+1}}$
Differenzengleichungen $y_{(k)}=\,$	$y_{(k)}=K\cdot u_{(k)}$	$y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}$	$[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}$	$K_{{PD1}}\cdot \left[u_{{(k)}}+(u_{{(k)}}-u_{{(k-1)}})\cdot {\frac {T}{\Delta t}}\right]$	$y_{(k-1)}+[K_{PT1}\cdot u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}$

(Mit K = Verstärkungsfaktor, $y_{(k)}$ = aktuelle Ausgangsgröße, $y_{(k-1)}$ = vorherige Ausgangsgröße, T = Zeitkonstante, $u_{(k)}$ = aktuelle Eingangsgröße)

Diese Differenzengleichungen von Elementarsystemen können beliebig multiplikativ, additiv oder zurückgekoppelt vermascht sein. Jede Gleichung eines Gesamtsystems wird hintereinander berechnet. Bei Reihenschaltungen von Teilsystemen ist die berechnete Ausgangsgröße $y_{(k)}$ die Eingangsgröße $u_{(k)}$ des folgenden Teilsystems. Bei Parallelschaltungen von Teilsystemen werden die Ergebnisse der Ausgangsgrößen additiv zusammengeführt.

Differenzengleichungen als Funktion der Ober- und Untersumme

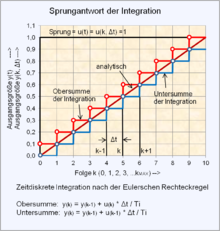
Definition der Obersumme und Untersumme der numerischen Integration.

In der numerischen Mathematik bedeuten die Flächen der Rechteckapproximation an eine gegebene analytische Funktion dann als Obersumme, wenn die Oberkante der Rechtecke oberhalb der analytischen Funktion anstößt. Umgekehrt handelt es sich um die Untersumme, wenn die Oberkante der Rechtecke unterhalb der analytischen Funktion anstößt. Für die numerische Berechnung interessiert nicht die Fläche der Rechtecke, sondern die Lage des Verlaufs der Stützstellen der Oberkante der Rechtapproximation.

Ein Wert einer Differenzengleichung nach der Obersumme zum Zeitpunkt $k=0;T_{A}=0$ ist differenzierbar. Der Funktionsunterschied der Obersumme zur Untersumme bedeutet beispielsweise, dass ein Eingangssignal als einzelner $\delta$ -Impuls zum Zeitpunkt t = 0 und Folge k = 0 in einem zeitdiskreten dynamischen System für den Zeitraum T_A – also zwischen k=0 und k=1 – wirksam wird. Differenzengleichungen nach der Untersumme können diesen $\delta$ -Impuls nicht erfassen.

Die Wertefolge der mit Differenzengleichungen berechneten Ausgangsfolge der Funktion der Untersumme unterscheiden sich von denen der Obersumme, dass die Wertefolge der Untersumme um einen Folgeschritt verzögert ist.

Differenzengleichungen höherer Ordnung

Differenzengleichungen höherer Ordnung entstehen dadurch, dass die Differentialquotienten einer Differentialgleichung höherer Ordnung durch Differenzenquotienten höherer Ordnung näherungsweise ersetzt werden. Die Anwendung einer solchen Differenzengleichung kann algebraisch sehr aufwendig werden.

Zeitkontinuierliche lineare Systeme werden im Zeitbereich durch die gewöhnlichen Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten für $n\geq m$ beschrieben. Dabei sind n und m die höchsten Ableitungen der Ausgangssignale y(t) und Eingangssignale u(t) .

Differenzengleichungen können auch aus gewöhnlichen Differentialgleichungen höherer Ordnung entwickelt werden, wenn ab dem Zeitpunkt $t=k\cdot \Delta t\geq 0$ die letzten vergangenen Ausgangs-Wertefolgen mit $k=[-1\to -n]$ und die Eingangs-Wertefolgen mit $k=[-1\to -m]$ bekannt sind.

Eine gegebene gewöhnliche Differentialgleichung wird durch den Koeffizienten $a_{0}$ dividiert, um y(t) freistellen zu können. Diese Form der Differentialgleichung wird entsprechend den dargestellten Koeffizienten wie folgt neu geordnet.

$y(t)+a_{1}{\dot {y}}(t)+a_{2}{\ddot {y}}(t)+\dots +a_{n}y^{(n)}(t)=b_{0}u(t)+b_{1}{\dot {u}}(t)+b_{2}{\ddot {u}}(t)+\dotsb +b_{m}u^{(m)}(t)$

Diese Differentialgleichung kann in eine Differenzengleichung überführt werden:

Als diskrete Zeit wird $h=\Delta t$ festgelegt.
$f(k\cdot T_{A})$ wird vereinfacht als $f_{{(k)}}$ geschrieben und entspricht der aktuellen Funktion des Folgegliedes.
Die kontinuierlichen Systemgrößen $y(t)\to y_{{(k)}}$ und $u(t)\to u_{{(k)}}$ werden zeitdiskret dargestellt.
Die Ableitungen im Zeitbereich werden entsprechend der Ordnung durch Differenzenquotienten $\Delta y/\Delta t$ der zugehörigen Ordnung ersetzt.

Jede Ableitung der Systemgrößen wird im zeitdiskreten Bereich entsprechend der Ordnung als zurückliegende Folgeglieder der Eingangs- und Ausgangsfolgen k-1 bis k-n oder k-m berücksichtigt.

Daraus folgt die Differenzengleichung:

$y_{(k)}+a_{1}\cdot y_{(k-1)}+a_{2}\cdot y_{(k-2)}+\dotsb +a_{n}\cdot y_{(k-n)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dotsb +b_{m}\cdot u_{(k-m)}$ .

Damit kann die allgemeine Form der Differenzengleichung nach $y_{(k)}$ aufgelöst werden:

$y_{(k)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dotsb +b_{m}\cdot u_{(k-m)}-a_{1}\cdot y_{(k-1)}-a_{2}\cdot y_{(k-2)}-\dotsb -a_{n}\cdot y_{(k-n)}$ .

Für die numerische Berechnung eines dynamischen Systems wird die Übertragungsfunktion G(s) oder die zugehörige Differentialgleichung benötigt. Die Umsetzung einer systembeschreibenden Differentialgleichung in eine angenäherte Differenzengleichung zur Beschreibung von Eingangsfolgen und Ausgangsfolgen eines dynamischen Systems wird ermöglicht, wenn die Differentiale der Differentialgleichung durch Rückwärts-Differenzenquotienten über die Abtastperiode ersetzt werden.>

Die folgenden Ableitungen der Differentialquotienten in Differenzenquotienten der 1. 2. und 3. Ordnung sind gegeben:

Differenzenquotient 1. Ordnung:

${\dot {y}}(t)={\frac {dy}{dt}}\approx {\frac {\Delta y}{\Delta t}}:={\frac {\Delta y_{(k)}}{h}}={\frac {y_{(k)}-y_{(k-1)}}{h}}$

Der Differenzenquotient 2. Ordnung entsteht aus Differenzen der Differenz:

${\ddot {y}}(t)={\frac {d^{2}y}{dt^{2}}}\approx {\frac {\Delta ^{2}y_{k}}{h^{2}}}={\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{h^{2}}}$

Der Differenzenquotient 3. Ordnung lautet:

$y^{(3)}(t)={\frac {d^{3}y}{dt^{3}}}\approx {\frac {\Delta ^{3}y_{k}}{h^{3}}}={\frac {y_{(k)}-3y_{(k-1)}+3y_{(k-2)}-y_{(k-3)}}{h^{3}}}$

Nach erfolgtem Einsetzen der Differenzenquotienten in die Differenzengleichung eines dynamischen Systems lassen sich die neuen Koeffizienten aus den Koeffizienten der Differentialgleichung berechnen.

Beispiel der Entwicklung einer Differenzengleichung zur Berechnung der Sprungantwort eines $PT2_{{kk}}$ -Gliedes mit konjugiert komplexen Polen:

Sprungantwort eines PT2-Gliedes mit konjugiert komplexen Polen. Δt = 0,01 s.
$0{,}25{\ddot y}(t)+0{,}125{\dot y}(t)+y(t)=1(t)$

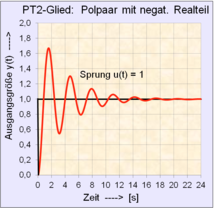
Gegeben: Übertragungsfunktion im s-Bereich:

$G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{0{,}25s^{2}+0{,}125s+1}}$

Sprungfunktion: u(t)=1

Gesucht: Differenzengleichung $y_{(k)}$ 2. Ordnung zur numerischen Bestimmung des System-Zeitverhaltens.
Zugehörige Differentialgleichung nach dem Differentiationssatz der Laplace-Transformation:

$0{,}25{\ddot {y}}(t)+0{,}125{\dot {y}}(t)+y(t)=u(t)$

Die Differenzenquotienten für ${\ddot y}(t)$ und ${\dot y}(t)$ werden in die nachfolgende Differenzengleichung eingesetzt:

$0{,}25\cdot {\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{h^{2}}}+0{,}125\cdot {\frac {y_{(k)}-y_{(k-1)}}{h}}+y_{k}=u_{k}\quad |\qquad y(t)\to y_{(k)};\ u(t)\to u_{(k)}$

Die Brüche werden in einzelne additive Terme aufgelöst, um $y_{(k)}$ freistellen zu können, Hilfsgröße $\psi$ eingeführt:

$y_{(k)}{\bigg (}{\frac {0{,}25}{h^{2}}}+{\frac {0{,}125}{h}}+1{\bigg )}:=y_{(k)}\cdot \psi =u_{(k)}+{\frac {0{,}5y_{(k-1)}}{h^{2}}}-{\frac {0{,}25y_{(k-2)}}{h^{2}}}+{\frac {0{,}125y_{(k-1)}}{h}}$

$y_{(k)}={\frac {u_{(k)}}{\psi }}+{\frac {0{,}5y_{(k-1)}}{\psi \cdot h^{2}}}-{\frac {0{,}25y_{(k-2)}}{\psi \cdot h^{2}}}+{\frac {0{,}125y_{(k-1)}}{\psi \cdot h}}\quad {\bigg |}\qquad \psi ={\frac {0{,}25}{h^{2}}}+{\frac {0{,}125}{h}}+1;\quad u_{(k)}=1$

Berechnungsbeispiel für einige Werte der Ausgangsfolge $y_{(k)}$ mit $h=0{,}01;\ \psi =2513{,}5;$ Sprung $u_{(k)}=1$ :

$t_{0}=0{,}00\,\mathrm {s} ;\qquad y_{(k=0)}=0{,}0004+0-0+0=0{,}0004$ .

$t_{1}=0{,}01\,\mathrm {s} ;\qquad y_{(k=1)}=0{,}0004+0{,}0008-0+0=0{,}0012$ .

$t_{2}=0{,}02\,\mathrm {s} ;\qquad y_{(k=2)}=0{,}0004+0{,}0024-0{,}0004+0=0{,}0024$ .

$t_{157}=1{,}57\,\mathrm {s} ;\qquad y_{(k=157)}=0{,}0004+3{,}286-1{,}643+0{,}008=1{,}652$ .

Diese Differenzengleichung entspricht einem Rekursionsalgorithmus eines dynamischen Systems, der schrittweise mit einem Personal-Computer gelöst werden kann.

Die rekursive Berechnung der Differenzengleichung 2. Ordnung bezieht sich für die aktuelle Ausgangsfolge $y_{(k)}$ durch Einsetzen der zurückliegenden Werte der Ausgangsfolge $u_{{(k-1)}}$ und $u_{(k-2)}$ in die Gleichung. Für das 1. Folgeglied der Berechnungsfolge k=0 sind die zurückliegenden Werte der Ausgangsfolge noch nicht verfügbar und damit Null. Die Anzahl $k=(0,1,2,3,\dotsc ,k_{\mathrm {max} })$ der Glieder der Ausgangsfolge wird durch die diskrete Zeit $h=\Delta t$ und durch die gewünschte zu beobachtende Gesamtzeit des Einschwingvorgangs bestimmt.

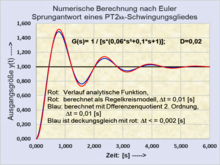
Sprungantwort eines PT2-Schwingungsgliedes nach zwei Berechnungsmethoden.

Beispiel zur Berechnung eines $PT2_{(kk)}$ -Gliedes durch eine einfachere Methode als Modellregelkreis:

Nachdem bereits dargestellt wurde, dass laut Systemtheorie nur Übertragungsfunktionen G(s) 1. und 2. Ordnung oder Produkte dieser Systeme existieren, lassen sich PT2-Glieder (Schwingungsglieder) über Differenzengleichungen 1. Ordnung über einen Modellregelkreis erheblich einfacher berechnen und simulieren. Dazu werden 2 Differenzengleichungen mit je einem I-Glied und einem PT1-Glied als offener Modellregelkreis mit einer zusätzlichen Schließbedingung der Regelabweichung $e=w-y$ definiert.

Der Modellregelkreis erzwingt mit den geeigneten Parametern für das -Glied und das $PT1$ -Glied, dass die Ausgangsgröße $y_{(k)}$ einem System $PT2_{(kk)}$ -Glied (Schwingungsglied) mit konjugiert komplexen Polen entspricht.

Ein weiterer Vorteil liegt darin, dass die numerische Berechnung mit Differenzengleichungen 1. Ordnung schneller ist, als die Berechnung von Differenzengleichungen 2. Ordnung.

Beispiel der Simulation eines $PT2_{{kk}}$ -Schwingungsgliedes mit zwei Differenzengleichungen 1. Ordnung:

Aufgeschnittener Modellregelkreis:

$G_{0}(s)={\frac {Y}{W}}(s)={\frac {K_{H}}{s\cdot (T_{H}\cdot s+1)}}$

Die Übertragungsfunktion des Modellregelkreises:

$G(s)=G_{0}/(1+G_{0})$ lautet in der allgemeinen Form für ein $PT2_{{kk}}$ -Schwingungsglied:

$G_{H}(s)={\frac {Y}{W}}(s)={\frac {G_{0}}{1+G_{0}}}={\frac {1}{{\frac {T_{H}}{K_{H}}}\cdot s^{2}+{\frac {1}{K_{H}}}\cdot s+1}}\ {\mathrel {\hat {=}}}\ {\frac {1}{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}={\frac {1}{a\cdot s^{2}+b\cdot s+1}}$

Durch Koeffizientenvergleich lassen sich die gewünschten Parameter $K_{H}$ und $T_{H}$ des offenen Modellregelkreises bestimmen:

${\frac {T_{H}}{K_{H}}}=a;\qquad {\frac {1}{K_{H}}}=b;\qquad T={\sqrt {a}}$ = Zeitkonstante des PT2-Gliedes.

Mit diesen Parametern kann die numerische Berechnung mit den nachstehend aufgeführten Differenzengleichungen durchgeführt werden.

$T_{H}=a\cdot K_{H}={\frac {a}{b}};\qquad K_{H}={\frac {1}{b}};\qquad {\text{Dämpfung}}\ D={\frac {b}{2\cdot T}}$

Mit dem Vergleich Regelabweichung = Sollwert − Istwert wird der aufgeschnittene Regelkreis geschlossen ( $w_{(k)}$ = normierte Führungsgröße = 1):

Regelabweichung: $e_{{(k)}}=w_{{(k)}}-y_{{(k-1)}}$

Die beiden Differenzengleichungen der Einzelglieder lauten:

I-Glied: $u_{(k)}=u_{(k-1)}+e_{(k)}\cdot K_{H}\cdot \Delta t$

PT1-Glied: $y_{(k)}=y_{(k-1)}+[u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T_{H}+\Delta t}}$

Werden diese 3 Gleichungen tabellarisch hintereinander berechnet und jeweils das Ergebnisse der 1. Gleichung in die 2. Gleichung und dieses Ergebnis in die 3. Gleichung eingesetzt, entsteht die Berechnungsfolge $y_{(k)}$ des PT2-Gliedes mit gewählten z.B. 100 bis 1000 Folgen als Sprungantwort. Das Verfahren der Approximation über den Modellregelkreis ist gegenüber dem Verfahren mit dem Differenzenquotienten 2. Ordnung vorzuziehen, weil algebraisch einfacher und $\Delta t$ für die gleiche Genauigkeit der Approximation etwa 3-fach größer sein kann.

Genauigkeit der numerischen Berechnung des Euler-Streckenzugverfahrens

Man bezeichnet ein numerisches Verfahren als stabil, wenn die Approximationsfehler im Laufe der Berechnung nicht anwachsen.

Es sind die Verläufe der numerischen Lösung $y_{(k)}=f(x_{(k)})$ zu unterscheiden:

Verhalten der Exponentialfunktion zum monoton strebenden Maximum

Für eine Auflösung von $h=\Delta x=0{,}01$ bzw. $\Delta t=0{,}01$ kann im Allgemeinen eine Genauigkeit mit einem Approximationsfehler bezogen auf einen Endwert von ca. 1 % erzielt werden, wenn $1/h=100$ Folgen berechnet werden.

Liegt ein Anfangswert der Exponentialfunktion $y_{(0)}>0$ vor, beispielsweise $y_{(0)}=1$ , der nicht bekannt ist, startet die numerische Berechnung bei $y_{{(0)}}=0$ . Wird ein Funktionsendwert der Größe $y_{(k=max)}=10$ betrachtet, liegt der Approximationsfehler durch den vernachlässigten Anfangswert bei 10 %. Hat der Funktionsendwert die Größe $y_{(k=max)}=100$ , liegt der Approximationsfehler durch den vernachlässigten Anfangswert bei 1 %, dem sich der übliche Diskretisierungsfehler $f(h)$ überlagert.

Verhalten einer Exponentialfunktion mit asymptotischen Anstieg auf einen Endwert

Bei dynamischen Systemen im Zeitbereich startet die numerische Berechnung von $y_{{(0)}}=0$ oder $y_{(0)}>0$ für eine Auflösung $\Delta t=0{,}01$ und erreicht asymptotisch einen Endwert in minimal $1/{\Delta t}=100$ Folgen oder beliebig mehr Folgen. Der Approximationsfehler liegt bei 1 % bezogen auf den Endwert.

Die Anzahl der Folgen $k_{\mathrm {max} }$ kann beliebig erhöht werden, um einen größeren Zeitabschnitt zu betrachten. Der Approximationsfehler ändert sich nicht, solange ${\Delta t}$ nicht geändert wird.

Differenzengleichungen, welche die Obersumme in Annäherung an eine analytische Funktion berechnen, ergeben immer einen kleinen Anfangswert für $y_{(0)}>0$ , der sich aus den Parametern der Differenzengleichung ergibt. Dieser Wert ist in der Regel kleiner als $y_{(2-h)}=y_{(1)}$ .

Differenzengleichungen 2. Ordnung als Schwingungsglieder

Differenzengleichungen 2. Ordnung, die dynamische Systeme im Zeitbereich beschreiben, stellen sich für eine Dämpfung $0<D<1$ mit konjugiert komplexen Polen als Schwingungsglied dar. Solche Systeme enthalten gedämpfte sinusförmige Schwingungen, die mit schnellen Anstiegs- und Abfallgeschwindigkeiten auftreten. Für die Betrachtung der Genauigkeit der Approximation ist maßgebend, wieviel Folgen innerhalb der ersten Schwingung mit dem steilsten Gradienten stattfinden.

Die größte Änderungsgeschwindigkeit einer gedämpften sinusförmigen Schwingung liegt beim 1. Nulldurchgang und vermindert sich mit jedem weiteren Nulldurchgang.

In grober Annäherung an die analytische Funktion mit der Asymptote 1 sollte der ersten positiven Halbwelle eine Auflösung von mehr als 100 Folgen mit $>100\cdot \Delta t$ gegeben werden. Der zu erwartende maximale Approximationsfehler für $y_{(k)}=f(\Delta t=0{,}003)$ liegt bei ca. 1 %.

Die Anzahl der Folgen für einen zu betrachtenden Zeitraum $k_{\mathrm {max} }\cdot \Delta t$ hat keinen Einfluss auf die Genauigkeit.

z-Transformation für Abtastsysteme linearer Übertragungssysteme

Durch die z-Transformation können aus impulsförmig abgetasteten Signalen und Differenzengleichungen gebrochen rationale Funktionen als z-Übertragungsfunktion entstehen. Damit vereinfachen sich insbesondere in der Regelungstechnik durch z-Verschiebungssätze die Überführung in eine neue erweiterte Differenzengleichung und damit Festlegung des Regelalgorithmus für einen Mikrorechner.

Grundlagen der z-Transformation für lineare Abtastsysteme (Online Prozess)

Die Anwendung der z-Transformation bezieht sich ausschließlich auf Digitalrechner-geführte Anlagen, die Steuer- und Regelungstechnik und digitale Filter.

Vergleich der z-Transformation und der Laplace-Transformation.
Mit $z=e^{{s\cdot T_{A}}}$ wird die s-Ebene auf die z-Ebene abgebildet.

Die z-Transformation ist eine mathematische Methode, um zyklisch abgetastete kontinuierliche Signale im Zusammenhang mit dynamischen Systemen im z-Bereich berechenbar zu machen (vgl. Matched-Z-Transformation). Sie ist eine Transformation von Abtastfolgen, die im Vergleich zur Behandlung von Differentialgleichungen ähnliche Eigenschaften aufweist, wie die Laplace-Transformation.

Mit den Methoden der z-Transformation lassen sich Differenzengleichungen von abgetasteten Signalfolgen ermitteln.

Sollen die analogen Signale dynamischer Systeme in einem Computer bearbeitet werden, ist eine Digitalisierung der Signale erforderlich. Dabei werden die analogen Signale im Rhythmus der Abtastzeit T_A abgetastet und mittels AD-Wandlern digitalisiert.

Bei dynamischen Systemen mit Signalabtastung ist die Ausgangswertefolge mit der Folge $k=[0;1;2;3;\dotsc ]$ eine unbegrenzte Folge. Im Gegensatz dazu handelt es sich bei der Simulation eines Systemverhaltens mit der Berechnungsfolge $k=[0;1;2;3;\dotsc ;k_{\mathrm {(max)} }]$ mit der diskreten Zeit $\Delta t$ um eine begrenzte Folge, die eine Nummerierung der Werte darstellt.

Die Eingangsfolgen werden durch einen Mikrocomputer zu Ausgangsfolgen berechnet. Diese Abtastzeit T_A ist eine reale Zeit.

Entsprechend den Eigenschaften der z-Transformation F(z) ergeben sich folgende Operationen:

Spezielle Rechenoperationen:

Rechtsverschiebung, Linksverschiebung, Differenzensatz, Summensatz usw., zurückliegende Berechnungsfolgen sind zu speichern.

Überführung des dynamischen Systems als z-Übertragungsfunktion,
Eigenschaften des z-Bildbereichs ähnlich der Laplace-Transformation:

z-Blockdarstellung von reihen- und parallelgeschalteten Systemen, Pol-Nullstellenzerlegung, Stabilitätsbetrachtung, Berechnungsregeln und die Überführung vom z-Bildbereich in den diskreten Zeitbereich $f_{{(k)}}$ .

Definition Signalabtastung:

Bei einem gegebenen Hardwaresystem wird das Eingangssignal (z.B. Regeldifferenz $e_{{(k)}}$ ) im zeitlichen Abstand der Abtastzeit T_A abgetastet, digitalisiert und als Eingangswertefolge in einen Mikrorechner geleitet. Meist handelt es sich bei diesem System um den Regelalgorithmus eines Reglers als Differenzengleichung. Die Ausgangsfolge wird analogisiert und in ein Halteglied z.B. nullter Ordnung geleitet. Damit entsteht als Stellgröße ein gestuftes quasi stetiges Signal, das von einer kontinuierlich wirkenden Regelstrecke verarbeitet werden kann.

Liegt für andere Anwendungen das Eingangssignal bereits als diskretes Signal vor, gilt die gleiche Prozedur mit der Digitalisierung des Eingangssignals und der Eingangsfolge. Ein Mikrorechner verarbeitet fortlaufend die Eingangsfolge zu einer Ausgangsfolge über Differenzengleichungen mit einem spezifischen Systemverhalten. Bei den Werten der Ausgangsfolge handelt es sich um digitale Signale.

Bei diesen Anwendungen ist das Zeitintervall $T_{A}=\Delta t$ eine reale Zeit.

Differenzengleichungen können auch mit Hilfe der z-Transformation aus der z-Übertragungsfunktion entstehen.

z-Übertragungsfunktion

Wendet man den Rechtsverschiebungssatz der z-Transformation auf Differenzengleichungen an, so erhält man daraus direkt als Verhältnis der z–Transformierten von Eingangs- und Ausgangsfolge die z–Übertragungsfunktion des diskreten Systems. Zu der Anwendung mit linearen Systemen folgende Informationen:

Die Differenzengleichungen $y_{(k)}$ können ausschließlich mit Hilfe des Linearitätssatzes und Verschiebungssatzes in den komplexen z-Bildbereich und in die z-Übertragungsfunktionen überführt werden.
Gegebene Übertragungsfunktionen des s-Bereiches in Verbindung mit Haltegliedern und Abtastelementen können ebenfalls mit Hilfe der z-Korrespondenztabellen als z-Übertragungsfunktion transformiert werden.
Die z-Übertragungsfunktion lautet:

$G(z)={\frac {Y(z)}{U(z)}}={\frac {{\text{Zählerpolynom}}\ (z)}{{\text{Nennerpolynom}}\ (z)}}$ .

Die Rücktransformation von der z-Übertragungsfunktion in den zeitdiskreten Bereich als Differenzengleichung erfolgt durch den invers angewendeten Linearitätssatz und Verschiebungssatz für alle einzelnen Terme.

Anwendung der z-Übertragungsfunktion in einem Regelkreis

Siehe auch z-Transformation.

Es können sowohl abgetastete Eingangssignale u(kT_A) als auch Differenzengleichungen f(kT_A), die im diskreten Zeitbereich das Verhalten eines Systems (z.B. den Regelalgorithmus eines Reglers) beschreiben, als z-Übertragungsfunktionen in den z-Bereich transformiert und als algebraische Gleichungen behandelt werden.

Wird eine inverse z-Transformation der z-Übertragungsfunktionen durchgeführt, entsteht die Lösung der zeitdiskreten Differenzengleichung $f_{{(k)}}={\mathcal Z}^{{-1}}\{F(z)\}$ im $f(kT_{A})$ -Bereich. Mit Hilfe verschiedener Verfahren der Rücktransformation vom z-Bereich in den zeitdiskreten k-Bereich ergeben sich dann als Lösung die Differenzengleichungen des Regelalgorithmus für den diskreten Bereich f(kT_A).

Die typische Anwendungsprozedur der z-Transformation an einem digitalen Systems, einem digitalen Regler oder einem digitalen Filter lautet für den Regelalgorithmus wie folgt:

Die Abtastfolge des Eingangssignals (Eingangsfolge) wird transformiert als z-Übertragungsfunktion ,
Die Differenzengleichung $f_{{(k\cdot T_{A})}}$ des gewünschten Reglerverhaltens wird transformiert als z-Übertragungsfunktion ,
Die z-transformierten Systeme werden algebraisch entsprechend den z-Rechenregeln zusammengefasst,
Mit der inversen z-Transformation des z-Produktes von Signal und Regelalgorithmus entsteht der Berechnungsalgorithmus des digitalen Reglers (Mikro Computers) wieder als Differenzengleichung.

Die Analyse und die Synthese diskreter Signale und Systeme lässt sich mit der z-Transformation erleichtern, setzt aber auch umfangreiches mathematisches Spezialwissen voraus, dass zum Teil auf ähnliche Regeln wie bei der Laplace-Transformation aufgebaut ist.

$\to$ Siehe Artikel z-Transformation.

Differenzengleichungen in der Ökonomie

In der ökonomischen Theorie kommen Differenzengleichungen vor allem zum Einsatz, um die Entwicklung ökonomischer Größen über die Zeit zu analysieren. Vor allem in der Wachstumstheorie und Konjunkturtheorie werden zeitliche Abläufe vielmals in Form von Differenzengleichungen abgebildet.

Man geht dabei davon aus, dass z.B. das Bruttoinlandsprodukt sich auf einem bestimmten Pfad hin zu einem langfristigen Gleichgewicht entwickelt, in dem alle Kapazitäten ausgelastet sind. Je nach Lösung der Differenzengleichung ergibt sich der Entwicklungspfad als asymptotischer Verlauf oder als schwingender Verlauf (in etwa Kosinus-Kurven). Es bleibt aber nicht aus, dass zur mathematischen Modellierung (z.B. beim Bruttoinlandsprodukt) einige vereinfachende Annahmen gemacht werden müssen (z.B. über die Lagerbildung, Konsum als Anteil des BIP oder Investitionssteigerung durch Gewinnerwartung).

Anwendung von Differenzengleichung 1. Ordnung

Ein weiteres klassisches Beispiel ist das Spinnwebtheorem (auch cobweb theorem). Die Entwicklung der Preise und Mengen folgt rekursiven Funktionen oder, mathematisch ausgedrückt, allgemeinen Differenzengleichungen erster Ordnung.

Anwendung von Differenzengleichung 2. Ordnung

Das Multiplikator-Akzelerator-Modell will erklären, warum das wirtschaftliche Wachstum nicht monoton verläuft, sondern typischerweise einem Konjunkturzyklus folgt. Das Modell lässt sich aus dem Wachstumsmodell von Harrod und Domar heraus entwickeln, eine besondere Variante stammt von Paul A. Samuelson (1939) und John Richard Hicks (1950).

Siehe auch

Literatur

Jan Lunze: Regelungstechnik 2, Mehrgrößensysteme, Digitale Regelung. 7. Auflage. Springer Verlag, 2013, ISBN 978-3-642-10197-7.
Krause, Nesemann: Differenzengleichungen und diskrete dynamische Systeme. Eine Einführung in Theorie und Anwendungen. 1999. Auflage. Vieweg+Teubner Verlag, 1999, ISBN 978-3-519-02639-6.

Basierend auf einem Artikel in:

Wikipedia.de