
D-Glied


Als D-Glied bezeichnet man ein LZI-Übertragungsglied in der Regelungstechnik, welches ein differenzierendes Übertragungsverhalten aufweist. D.h. der Wert der Ausgangsgröße ist abhängig von der Änderungsgeschwindigkeit der Eingangsgröße.
Die zugehörige Funktionalbeziehung im Zeitbereich lautet
,
so dass die komplexe Übertragungsfunktion im Bildbereich die Form
hat. Hierbei bezeichnet K, K > 0, die Übertragungskonstante bzw. den Verstärkungsfaktor des D-Gliedes.
Das D-Glied wird nur theoretisch betrachtet, da in der Sprungantwort ein Dirac-Impuls auftritt. Im realen System geht ein D-Glied immer mit einer Verzögerung einher.
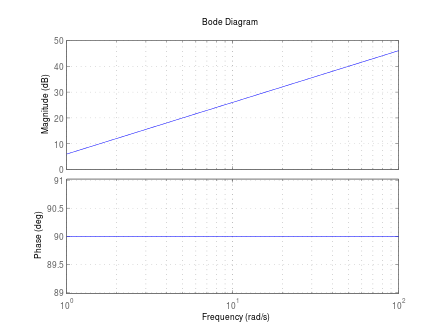
Bodediagramm
Beim D-Glied ist .
Daher gilt für den Amplituden-
und Phasengang im Bode-Diagramm:
Die Betragskennlinie ist also eine Gerade, die mit 20 dB/Dekade steigt und bei ω = 1 den Wert KdB hat. Aufgrund der linearen Steigung der Verstärkung hat ein ideales D-Glied für unendlich hohe Frequenzen eine unendlich hohe Verstärkung, was nicht durch ein reales System dargestellt werden kann. Die Phasenkennlinie ist konstant 90°.
Sprungantwort
Die Sprungantwort des D-Gliedes wird beschrieben durch ,
wobei
für die Delta-Funktion
steht.
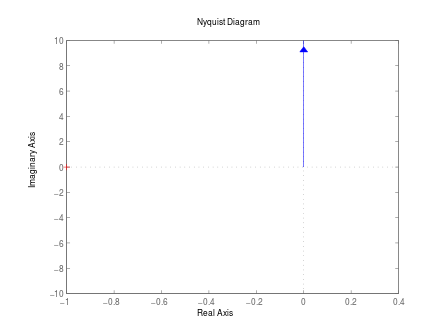
Ortskurve
Die Ortskurve ()
des D-Gliedes verläuft auf der positiven imaginären Achse vom Punkt Null für
gegen
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.09. 2025