PT1-Glied

PT₁-Glied im Strukturbild

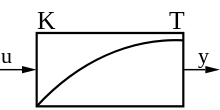
Als PT₁-Glied bezeichnet man ein LZI-Übertragungsglied in der Regelungstechnik, welches ein proportionales Übertragungsverhalten mit Verzögerung 1. Ordnung aufweist. Ein gebräuchliches Beispiel ist in der Elektrotechnik der Tiefpass (1. Ordnung).

Die zugehörige Funktionalbeziehung im Zeitbereich ist die Differentialgleichung

$T\cdot {\dot {y}}(t)+y(t)=K\cdot u(t)$ ,

so dass die komplexe Übertragungsfunktion im Bildbereich die Form

$G(s)={\frac {K}{1+T\cdot s}}$

hat. Hierbei bezeichnet K, K > 0, die Übertragungskonstante bzw. den Verstärkungsfaktor und T , T > 0, die Zeitkonstante.

Bodediagramm

Beim PT₁-Glied ist $G(j\omega )={\frac {K}{1+j\omega T}}$ der Frequenzgang. Daher gilt für den Amplituden- und Phasengang im Bodediagramm:

$|G(j\omega )|={\frac {K}{{\sqrt {1+\omega ^{2}T^{2}}}}}$

$\varphi (\omega )=-\arctan(\omega T)$

Amplitudengang

Bezeichnet $\omega _{0}={\frac {1}{T}}$ die Knick- bzw. Eckkreisfrequenz, so lässt sich der Amplitudengang grob in zwei Bereiche einteilen:

$G(j\omega )={\begin{cases}K,&{\mbox{wenn }}\omega \ll \omega _{0}\\{\frac {K}{{\frac {\omega }{\omega _{0}}}}},&{\mbox{wenn }}\omega \gg \omega _{0}\end{cases}}$

bzw.

$|G|_{{{\mathrm {dB}}}}={\begin{cases}20\log K,&{\mbox{wenn }}\omega \ll \omega _{0}\\20\log K-20\log {\frac {\omega }{\omega _{0}}},&{\mbox{wenn }}\omega \gg \omega _{0}\end{cases}}$

Für Kreisfrequenzen unterhalb der Eckkreisfrequenz liegt die Betragskennlinie des PT₁-Gliedes parallel zur 0-dB-Linie im Abstand von K_dB und für große Kreisfrequenzen fällt sie mit 20 dB/Dekade. Bei der Knickkreisfrequenz ω = ω₀ schneiden sich die beiden Asymptoten. Der tatsächliche Wert des Amplitudenganges weicht dort um −3 dB von der asymptotischen Näherung ab. Bei ω = 0,5 ω₀ bzw. ω = 2 ω₀ beträgt die Abweichung nur noch −1 dB.

Die Eckkreisfrequenz berechnet sich aus der Polstelle der Übertragungsfunktion, also der Nullstelle des Nenners 1 + Ts. Die Polstelle ist $-{\frac {1}{T}}$ und heißt Eigenwert, dessen Betrag die Eckkreisfrequenz ω₀ beschreibt.

Phasengang

Die Phasenverschiebung des PT₁-Gliedes beträgt bei kleinen Kreisfrequenzen 0°, bei großen Kreisfrequenzen −90° und bei der Knickkreisfrequenz ω₀ −45°.

Für die asymptotische Näherung zeichnet man eine Gerade, die eine Dekade vor der Knickkreisfrequenz bei 0° beginnt und eine Dekade nach der Knickkreisfrequenz bei −90° endet.

Bodediagramm eines PT₁-Gliedes (K = 2, T = 1)

Sprungantwort

Die Sprungantwort des PT₁-Gliedes wird beschrieben durch

$a(t)=K(1-{\mathrm {e}}^{{-{\frac {t}{T}}}})$

und hat den Verlauf einer e-Funktion. Der Verlauf nähert sich dem Endwert K an. Nach der Zeit t = T beträgt der Wert 0,63 K und nach t = 3 T bereits 0,95 K, es bleibt theoretisch aber immer eine minimale Abweichung vom Endwert erhalten. Die Tangente im Ursprung schneidet den Wert des Verstärkungsfaktors K nach der Zeit T. Der Betrag der Zeitkonstanten T bestimmt die Schnelligkeit des Gliedes.

Sprungantwort eines PT₁-Gliedes (K = 2, T = 1)

Ortskurve

Die Ortskurve ( $0\leq \omega \leq \infty$ ) des PT₁-Gliedes verläuft vom Punkt K auf der positiven reellen Achse durch den vierten Quadranten für $\omega \to \infty$ in den Punkt 0.

$F({\mathrm j}\omega )={\frac {K}{1+{\mathrm j}\omega T_{1}}}$

Komplex konjugiertes Erweitern liefert

$F({\mathrm j}\omega )={\frac {K}{1+{\mathrm j}\omega T_{1}}}\cdot {\frac {1-{\mathrm j}\omega T_{1}}{1-{\mathrm j}\omega T_{1}}}={\frac {K-{\mathrm j}\omega T_{1}K}{1+\omega ^{2}T_{1}^{2}}}$

sodass sich Real- und Imaginärteil explizit darstellen lässt:

${\mathrm {Re}}\left\{F({\mathrm j}\omega )\right\}={\frac {K}{1+\omega ^{2}T_{1}^{2}}}$

${\mathrm {Im}}\left\{F({\mathrm j}\omega )\right\}={\frac {-\omega T_{1}K}{1+\omega ^{2}T_{1}^{2}}}$

Damit errechnet sich Betrag und Phase

$\left|F\left({\mathrm j}\omega \right)\right|={\frac {K}{{\sqrt {1+\omega ^{2}T_{1}^{2}}}}}$

$\varphi (\omega )=\varphi \left(F({\mathrm j}\omega )\right)=\arctan(-\omega T_{1})=-\arctan(\omega T_{1})$

Die Extremwerte ergeben sich folgendermaßen:

${\mathrm {Re}}\left\{F({\mathrm j}\omega \to 0)\right\}=K$

${\mathrm {Im}}\left\{F({\mathrm j}\omega \to 0)\right\}=0$

${\mathrm {Re}}\left\{F({\mathrm j}\omega \to \infty )\right\}=0$

${\mathrm {Im}}\left\{F({\mathrm j}\omega \to \infty )\right\}=0$

$|F({\mathrm j}\omega \to 0)|=K$

$\varphi ({\mathrm j}\omega \to 0)=0^{\circ }$

$|F({\mathrm j}\omega \to \infty )|=0$

$\varphi ({\mathrm j}\omega \to \infty )=-90^{\circ }$

Ortskurve eines PT₁-Gliedes (T = 1, K = 2)

Zeitdiskretes PT1-Glied

Das Verhalten eines PT1-Gliedes lässt sich mit der folgenden Formel zeitdiskret berechnen. Sie ist Grundlage zur Nachbildung dieses Reglertypes in der digitalen Signalverarbeitung.

Aus obiger Differentialgleichung folgt mit $\Delta t$ als der Schrittweite der Abtastung die Differenzengleichung:

$T\cdot {\frac {y_{{n}}-y_{{n-1}}}{\Delta t}}+y_{{n}}=Ku_{{n}}$