
Proportionalität
Zwischen zwei veränderlichen Größen besteht Proportionalität, wenn sie immer in demselben Verhältnis zueinander stehen.
Grundlagen
Proportionale Größen sind verhältnisgleich; das heißt, bei den proportionalen
Größen
und
ist die Verdopplung (Verdreifachung, Halbierung, …) der Größe
stets mit einer Verdopplung (Verdreifachung, Halbierung, …) der Größe
verbunden, oder allgemein gesagt: Die Größe
geht aus der Größe
durch Multiplikation mit einem immer gleichen Faktor hervor. Das Verhältnis
wird Proportionalitätsfaktor oder Proportionalitätskonstante
genannt.
Beispiele:
- Der Kreisumfang ist proportional dem Kreisdurchmesser; der
Proportionalitätsfaktor ist die Kreiszahl
= 3,14159…
- Bei einem Kauf ist die Mehrwertsteuer proportional dem Nettopreis; der Proportionalitätsfaktor ist der Mehrwertsteuersatz, beispielsweise 0,19 (= 19 %).
- Die Masse einer Flüssigkeit ist (bei sonst gleichen Bedingungen) proportional ihrem Volumen (siehe ausführliches Beispiel unten).
Proportionalität ist ein Spezialfall der Linearität. Für eine lineare Funktion mit zwei reellen Größen ist jeder Zusammenhang zwischen den Größen dann linear, wenn dessen Darstellung in einem kartesischen Koordinatensystem eine Gerade ist. Proportionalität bedeutet hierbei, dass diese Gerade durch den Nullpunkt (Koordinatenursprung) geht (Ursprungsgerade); der Proportionalitätsfaktor bestimmt deren Steigung.
Gelegentlich wird auch von direkter Proportionalität gesprochen im Gegensatz zur indirekten, inversen, umgekehrten oder reziproken Proportionalität, bei der eine Größe proportional dem Kehrwert der anderen Größe ist; statt des Verhältnisses ist hierbei also das Produkt der beiden Größen konstant. Der Graph ist eine Hyperbel und geht nicht durch den Nullpunkt.
Der Kalkül des Dreisatzes setzt eine proportionale Funktion voraus.
Mathematische Definition
Historische Definition
Euklid, Elemente Buch V, Definitionen 3–6.
Definition 5 lautet:
„Man sagt, dass Größen in demselben Verhältnis stehen, die erste zur zweiten wie die dritte zur vierten, wenn bei beliebiger Vervielfachung die Gleichvielfachen der ersten und dritten den Gleichvielfachen der zweiten und vierten gegenüber, paarweise entsprechend genommen, entweder zugleich größer oder zugleich gleich oder zugleich kleiner sind.“
Definition 6:
„Und die dieses Verhältnis habenden Größen sollen in Proportion stehend heißen.“
Aktuelle Definition
Eine proportionale Funktion
ist eine homogene
lineare Zuordnung zwischen Argumenten
und ihren Funktionswerten
:
mit einem konstanten Proportionalitätsfaktor .
Dabei ist der Faktor
nicht sinnvoll.
Da es bei Proportionalität gleichwertig ist, ob die Größe
aus der Größe
durch Multiplikation mit einem immer gleichen Faktor hervorgeht, oder umgekehrt
aus
,
gilt ferner
;
dabei ist der Faktor
unzulässig.
Zwei Variable,
für die das Verhältnis zusammengehöriger Werte
und
konstant ist, heißen proportional zueinander
.
Proportionalität liegt demnach genau dann vor, wenn dieses Verhältnis
konstant ist; wenn es reell ist, kann es positiv oder
negativ sein.
Beispiel
Dichte

Die Tabelle gibt die Masse verschiedener Volumina von Öl an:
| Volumen |
Masse |
|---|---|
| 1 | 0,8 |
| 3 | 2,4 |
| 7 | 5,6 |
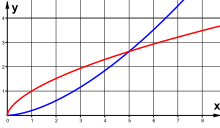
Die drei Wertepaare sind im Bild (rechts) als Punkte markiert. Berechnet man
den Quotienten ,
Masse/Volumen, so erhält man stets denselben Wert 0,8 t/m3. Allgemein
gibt der Quotient
die Steigung der Geraden an und ist zugleich der Proportionalitätsfaktor der
Zuordnung, hier mit der Bedeutung der Dichte des Öls. Auch
der umgekehrte Quotient
ist eine Proportionalitätskonstante, in diesem Fall mit der Bedeutung des spezifischen
Volumens. Im Beispiel erhält man
- Volumen/Masse = 1,25 m3/t
Luftdruckänderung
Der Luftdruck ist abhängig von der Höhe über dem Meeresspiegel. In erdnahen
Schichten ist die Druckänderung
proportional zur Höhenänderung
mit
und mit der Proportionalitätskonstante für diese Änderungen ,
siehe Barometrische
Höhenformel.
Das Minuszeichen bedeutet: Beim Hochsteigen einer Treppe (positives )
nimmt der Druck ab (negatives
).
Schreibweise
Für „a proportional zu b“ verwendet man das Tilde-Zeichen ~:
Ebenfalls genormt ist die Schreibweise:
Das Zeichen
leitet sich aus dem mittelalterlichen æ
für lat. aequalis, dem Vorgänger des Gleichheitszeichens
ab.
| Zeichen | HTML | TeX | Unicode | ASCII |
|---|---|---|---|---|
| ~ | ~ oder ~ |
\sim |
U+007E | 126 |
| ∼ | ∼ oder ∼ |
U+223C | – | |
| ∝ | ∝ oder ∝ |
\propto |
U+221D | – |
Verwandte Begriffe
Es wird von Überproportionalität zwischen zwei Größen gesprochen, wenn
die eine sich immer stärker ändert als die andere. Entsprechend spricht man von
Unterproportionalität bei einer systematisch schwächeren Änderung der
anderen Größe. „Stärker“ und „schwächer“ bedeuten hierbei, wenn man es auf die
Formulierung mit der Gleichung
mit einem Exponenten
bezieht, dass bei normaler Proportionalität
,
bei Überproportionalität
und bei Unterproportionalität
gilt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.08. 2022