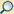Hyperreelle Zahl

In der Mathematik sind hyperreelle Zahlen ein zentraler Untersuchungsgegenstand der Nichtstandardanalysis. Die Menge der hyperreellen Zahlen wird meist als ${}^{*}\mathbb {R}$ geschrieben; sie erweitert die reellen Zahlen um infinitesimal benachbarte Zahlen sowie um unendlich große (infinite) Zahlen.

Als Newton und Leibniz ihre Differentialrechnung mit „Fluxionen“ bzw. „Monaden“ durchführten, benutzten sie infinitesimale Zahlen, und noch Euler und Cauchy fanden sie nützlich. Trotzdem wurden diese Zahlen von Anfang an skeptisch betrachtet, und im 19. Jahrhundert wurde die Analysis durch die Einführung der epsilon-delta-Definition des Grenzwertes und die Definition der reellen Zahlen durch Cauchy, Weierstraß und andere auf eine strenge Grundlage gestellt, die ohne infinitesimale Größen auskommt.

Abraham Robinson zeigte dann in den 1960er Jahren, auf welche Weise unendlich große und kleine Zahlen streng formal definiert werden können, und eröffnete so das Gebiet der Nichtstandardanalysis. Die hier gegebene Konstruktion ist eine vereinfachte, aber nicht minder strenge Version, die zuerst von Lindstrom gegeben wurde.

Durch die hyperreellen Zahlen ist eine Formulierung der Differential- und Integralrechnung ohne den Grenzwertbegriff möglich.

Elementare Eigenschaften

Die hyperreellen Zahlen ${}^{*}\mathbb {R}$ bilden einen geordneten Körper, der $\mathbb {R}$ als Teilkörper enthält. Beide sind reell abgeschlossen.

Infinitesimale (ε) und Infinite (ω) auf der hyperreellen Zahlengerade

Der Körper ${}^{*}\mathbb {R}$ wird so konstruiert, dass er elementar äquivalent zu $\mathbb {R}$ ist. Das bedeutet, dass jede Aussage, die in $\mathbb {R}$ gilt, auch in ${}^{*}\mathbb {R}$ gilt, falls die Aussage sich in der Prädikatenlogik erster Stufe über der Signatur $\{0,1,+,-,\cdot,<\}$ formulieren lässt.

Die Signatur bestimmt, welche Symbole man in den Aussagen gebrauchen darf. Die Einschränkung auf die Prädikatenlogik erster Stufe bedeutet, dass man nur über Elemente des Körpers quantifizieren kann, nicht jedoch über Teilmengen. Folgende Aussagen gelten z.B. sowohl in $\mathbb {R}$ als auch in ${}^{*}\mathbb {R}$ :

$\forall x \ \exists y\ x < y$
$\forall x\ x<x+1$
Jede Zahl, die größer oder gleich Null ist, hat eine Quadratwurzel. In Formeln: $\forall x\ ((x>0\lor x=0)\rightarrow (\exists y\ x=y\cdot y))$

Das heißt nun nicht, dass $\mathbb {R}$ und ${}^{*}\mathbb {R}$ sich genau gleich verhalten; sie sind nicht isomorph. Zum Beispiel gibt es in ${}^{*}\mathbb {R}$ ein Element , das größer als alle natürlichen Zahlen ist. Dies lässt sich jedoch nicht durch eine Aussage der obigen Form ausdrücken, man braucht dazu unendlich viele:

$1 < w, 1+1 < w, 1+1+1 < w, 1+1+1+1 < w, \dotsc$

Eine solche Zahl gibt es in $\mathbb {R}$ nicht. Eine hyperreelle Zahl wie nennt man infinit oder unendlich, der Kehrwert einer unendlich großen Zahl ist eine infinitesimale Zahl.

Ein weiterer Unterschied: Die reellen Zahlen sind ordnungsvollständig, d. h. jede nichtleere, nach oben beschränkte Teilmenge von $\mathbb {R}$ besitzt ein Supremum in $\mathbb {R}$ . Diese Forderung charakterisiert die reellen Zahlen als geordneten Körper eindeutig, d.h. bis auf eindeutige Isomorphie. ${}^{*}\mathbb {R}$ ist hingegen nicht ordnungsvollständig: Die Menge aller endlichen Zahlen in ${}^{*}\mathbb {R}$ besitzt kein Supremum, ist aber z.B. durch obiges beschränkt. Das liegt daran, dass man zur Formulierung der Ordnungsvollständigkeit über alle Teilmengen quantifizieren muss; sie kann daher nicht in der Prädikatenlogik erster Stufe formalisiert werden.

Die hyperreellen Zahlen sind gleichmächtig zu den reellen Zahlen:

$|{}^*\mathbb{R}| = |\mathbb{R}| = 2^{\aleph_0}$

Konstruktion

Die Menge aller Folgen reeller Zahlen ( $\textstyle \mathbb {R} ^{\mathbb {N} }=\prod _{n=1}^{\infty }\mathbb {R}$ ) bilden eine Erweiterung der reellen Zahlen, wenn man die reellen Zahlen mit den konstanten Folgen identifiziert.

wird also mit der Folge $( 1; 1; 1; 1; 1; 1; \dotsc)$ ,

wird also mit der Folge $( 2; 2; 2; 2; 2; 2; \dotsc)$ identifiziert.

Die Prototypen für „unendliche große“ Zahlen sind in dieser Menge Folgen, die irgendwann größer als jede reelle Zahl werden, z.B. die Folge:

$A = ( 1; 10; 100; 1000; 10000; \dotsc)$

Auf $\R^{\N}$ kann man nun die Addition und Multiplikation gliedweise definieren:

$( 1; 1; 1; 1; 1; 1; \dotsc) + ( 2; 2; 2; 2; 2; 2; \dotsc) = ( 3; 3; 3; 3; 3; 3; \dotsc)$

Dadurch wird $\R^{\N}$ zu einem kommutativen unitären Ring, allerdings besitzt dieser Nullteiler und ist daher kein Körper. Es gilt z.B. für

$p = ( 1; 0; 1; 0; 1; 0; \dotsc)$

$q = ( 0; 1; 0; 1; 0; 1; \dotsc)$

die Gleichung

$p \cdot q=0$ ,

obwohl sowohl als auch ungleich null sind. Es müssen daher noch Folgen über eine Äquivalenzrelation identifiziert werden. Die Idee ist, dass Folgen äquivalent sind, wenn die Menge aller Stellen, wo sich die Folgen unterscheiden, eine unwesentliche ist. Was ist nun die Menge aller unwesentlichen Mengen? Insbesondere sollen ja Folgen äquivalent sein, wenn sie sich im Unendlichen gleich verhalten, wenn sie also nur an endlich vielen Stellen verschieden sind. Alle endlichen Mengen sind daher unwesentlich. Und das Beispiel mit und zeigt, dass für jede Teilmenge entweder die Teilmenge oder ihr Komplement unwesentlich ist. Unter anderem wird dann noch gebraucht, dass die Vereinigung zweier unwesentlicher Mengen unwesentlich ist, da die Äquivalenzrelation transitiv sein muss. Das führt zu einem Ultrafilter:

Ein Filter auf den natürlichen Zahlen ist eine Menge von Teilmengen der natürlichen Zahlen, für die gilt:

Die leere Menge liegt nicht in .
Wenn sie zwei Mengen enthält, dann auch deren Schnittmenge.
Wenn sie eine Menge enthält, dann auch deren Obermengen.

Ein Filter ist frei, wenn gilt:

enthält keine endlichen Mengen

Er ist ein Ultrafilter, falls gilt:

Wenn eine bestimmte Teilmenge nicht enthält, enthält deren Komplement.

Die Existenz eines freien Ultrafilters folgt aus dem Lemma von Zorn. Mit Hilfe dieses Ultrafilters lässt sich eine Äquivalenzrelation definieren:

$(x_0, x_1, x_2, \dotsc) \sim (y_0, y_1, y_2, \dotsc)$ , falls $\{n : x_n = y_n\} \in U$ .

Auf der Menge der Äquivalenzklassen, die mit ${}^*\mathbb{R} := {}^{\textstyle\mathbb{R}^{\mathbb{N}}}\!/\!{}_{\textstyle\sim}$ bezeichnet wird, kann nun die Addition und Multiplikation der Äquivalenzklassen über Repräsentanten definiert werden. Dies ist wohldefiniert, da ein Filter ist. Da sogar ein Ultrafilter ist, hat jedes Element außer 0 in ${}^{*}\mathbb {R}$ ein Inverses. Z.B. ist eine der beiden Folgen und äquivalent zu null, die andere zu eins.

Nun müssen wir auf ${}^{*}\mathbb {R}$ noch eine Ordnung definieren. Dies geschieht durch

$(x_{0},x_{1},x_{2},\dotsc )<(y_{0},y_{1},y_{2},\dotsc )$ , falls $\{n:x_{n}<y_{n}\}\in U$ .

Leicht wird klar, dass dieses eine totale Ordnung auf ${}^{*}\mathbb {R}$ definiert (für die Totalität ist wichtig, dass ein Ultrafilter ist).

Die Äquivalenzklasse der Folge ist größer als jede reelle Zahl, denn für eine reelle Zahl gilt

$\{n : w_n > r\} \in U$

Anschließend ist noch zu zeigen, dass der konstruierte Körper tatsächlich elementar äquivalent zu $\mathbb {R}$ ist. Dies geschieht durch einen Induktionsbeweis über den Aufbau der Formeln, wobei von den Ultrafilter-Eigenschaften Gebrauch gemacht wird.

Bemerkungen

Jedem Filter auf den natürlichen Zahlen entspricht ein Ideal des Ringes $\R^{\N}$ (aber nicht umgekehrt). Einem Ultrafilter entspricht dabei ein maximales Ideal, daher ist der Quotient ein Körper. Die Wahl eines nicht-freien Ultrafilters hätte zur Folge, dass der Körper der Äquivalenzklassen isomorph zum Ausgangskörper ist.
Diese Konstruktion ist ein Spezialfall der Ultrapotenz. Unter anderem heißt das, dass die Einbettung von $\mathbb {R}$ in ${}^{*}\mathbb {R}$ eine elementare Einbettung ist und dass ${}^*\mathbb{R}\ \omega_1$ -saturiert ist.
Aus den Axiomen der Mengenlehre (ZFC) plus der Kontinuumshypothese folgt, dass diese Konstruktion nicht von der Wahl des Ultrafilters abhängt. (Das bedeutet, dass unterschiedliche Ultrafilter zu isomorphen Ultraprodukten führen.)

Infinitesimale und unendlich große Zahlen

Eine hyperreelle Zahl heißt infinitesimal, wenn sie kleiner als jede positive reelle Zahl und größer als jede negative reelle Zahl ist. Die Zahl Null ist die einzige infinitesimale reelle Zahl, aber es gibt andere hyperreelle infinitesimale Zahlen, beispielsweise $a = (1; 0{,}1; 0{,}01; 0{,}001; \dotsc)$ . Sie ist größer als null, aber kleiner als jede positive reelle Zahl, denn der Ultrafilter enthält alle Komplemente endlicher Mengen.

Eine negativ infinitesimale Zahl ist größer als jede negative reelle Zahl und kleiner als jede positive reelle Zahl, z.B. $-a=(-1;-0{,}1;-0{,}01;-0{,}001;\dotsc )$ .

Eine hyperreelle Zahl heißt endlich, wenn es eine natürliche Zahl gibt mit -n < x < n , anderenfalls heißt unendlich. Die Zahl $A = ( 1; 10; 100; 1000; \dotsc)$ ist eine infinite Zahl. Beachte: Die Bezeichnung „unendlich groß“ bezeichnet meist eine Zahl, die größer ist als jede natürliche Zahl, „unendlich“ schließt aber auch Zahlen ein, die kleiner sind als jede ganze Zahl, wie $-A = ( -1; -10; -100; \dotsc)$ .

Eine von 0 verschiedene Zahl ist genau dann unendlich, wenn 1/x infinitesimal ist. Zum Beispiel ist $A = \tfrac{1}{a}$ .

Es lässt sich zeigen, dass jede endliche hyperreelle Zahl „sehr nah“ an genau einer reellen Zahl liegt. Genauer: Ist eine endliche hyperreelle Zahl, dann gibt es genau eine reelle Zahl $\operatorname{st}(x)$ , so dass $x-\operatorname{st}(x)$ infinitesimal ist. Die Zahl $\operatorname{st}(x)$ nennt man den Standardteil von , die Differenz zu ist der Nichtstandardteil. Die Abbildung st hat einige angenehme Eigenschaften: Für alle endlichen hyperreellen Zahlen , gilt:

$\operatorname{st}(x + y) = \operatorname{st}(x) + \operatorname{st}(y),$
$\operatorname{st}(xy) = \operatorname{st}(x) \operatorname{st}(y),$
$\operatorname{st}(x) = x$ genau dann, wenn reell ist

Wobei das insbesondere bedeutet, dass der Term auf der linken Seite definiert ist, dass also z.B. x+y endlich ist, falls sowohl als auch endlich sind. Die Menge der endlichen Zahlen bilden also einen Unterring in den hyperreellen Zahlen. Außerdem ist

$\operatorname{st}\left(\frac{1}{x}\right) = \frac{1}{\operatorname{st}(x)}$ , falls nicht infinitesimal ist,

Ferner gilt:

Die Abbildung st ist stetig bzgl. der Ordnungstopologie auf der Menge der endlichen hyperreellen Zahlen, sie ist sogar lokal konstant.

Die ersten zwei Eigenschaften (und die Folgerung $\operatorname{st}(0)=0, \operatorname{st}(1)=1$ aus der dritten Eigenschaft) besagen, dass st ein Ring-Homomorphismus ist.

Zum Beispiel ist die hyperreelle Zahl $g = ( 0; 0{,}9; 0{,}99; 0{,}999; \dotsc)$ gliedweise kleiner als $( 1; 1; 1; 1; \dotsc)$ , also ist g < 1 . Sie ist aber größer als jede reelle Zahl kleiner 1. Sie ist daher zur 1 infinitesimal benachbart und 1 ist ihr Standardteil. Ihr Nichtstandardteil (die Differenz zu 1) ist

$g - 1 = ( -1; -0{,}1; -0{,}01; -0{,}001; \dotsc) = -a$ .

Beachte aber, dass die reelle Zahl $0{,}999\dotso$ als Grenzwert der Folge gleich 1 ist.

Weitere Eigenschaften

Die hyperreellen Zahlen sind gleichmächtig zu den reellen Zahlen, denn die Mächtigkeit muss mindestens so groß wie die der reellen Zahlen sein, da sie die reellen Zahlen enthalten, und kann höchstens so groß sein, da die Menge $\R^\N$ gleichmächtig zu den reellen Zahlen ist. Die Ordnungsstruktur der hyperreellen Zahlen hat überabzählbare Konfinalität, d.h. es existiert keine unbeschränkte abzählbare Menge, also keine unbeschränkte Folge von hyperreellen Zahlen: Sei eine Folge von hyperreellen Zahlen durch Repräsentanten $(a_n)\in{}^*\R^\N$ gegeben. Dann ist die hyperreelle Zahl mit dem Repräsentanten $A\in\R^\N$ ,

$A_n = \max_{i\leq n} a_{in}$

eine obere Schranke. Es lassen sich also mit keiner Folge beliebig große hyperreelle Zahlen erreichen. Die Ordnung der hyperreellen Zahlen induziert eine Ordnungstopologie. Mittels dieser lassen sich die üblichen topologischen Begriffe von Grenzwerten und Stetigkeit auf die hyperreellen Zahlen übertragen. Als geordneter Körper weisen sie mit der Addition eine mit der Topologie verträgliche Gruppenstruktur auf, es handelt sich also um eine topologische Gruppe. Diese induziert eine uniforme Struktur, sodass man auf den hyperreellen Zahlen auch von gleichmäßiger Stetigkeit, Cauchyfiltern etc. sprechen kann. Aus der überabzählbaren Konfinalität folgt durch Betrachtung von Kehrwerten, dass es auch keine Folge bestehend aus von 0 (oder entsprechend einer beliebigen anderen hyperreellen Zahl) verschiedenen hyperreellen Zahlen gibt, die beliebig nah an die 0 gelangt. Daher erfüllt die Topologie der hyperreellen Zahlen nicht die beiden Abzählbarkeitsaxiome, sie ist also insbesondere nicht metrisierbar. Aus der überabzählbaren Konfinalität folgt auch, dass sie nicht separabel sind. Aus dem Nichtvorhandensein von Suprema zahlreicher Mengen folgt, dass der Raum total unzusammenhängend und nicht lokalkompakt ist.

Siehe auch

Erweiterte reelle Zahl

Literatur

Heinz-Dieter Ebbinghaus et al.: Zahlen. 3. Auflage. Springer, Berlin/Heidelberg 1992, ISBN 3-540-55654-0.

Basierend auf einem Artikel in:

Wikipedia.de