Diskrete Wahrscheinlichkeitsverteilung
Eine diskrete (Wahrscheinlichkeits-)verteilung bzw. ein diskretes Wahrscheinlichkeitsmaß ist ein spezielles Wahrscheinlichkeitsmaß in der Stochastik. In Gegensatz zu den allgemeinen Wahrscheinlichkeitsmaßen sind die diskreten Wahrscheinlichkeitsverteilungen leicht zu handhaben, da sie nur auf mathematisch "kleinen" Mengen definiert sind. Dies verhindert einerseits das Auftreten von Paradoxien wie sie der Satz von Vitali zeigt und die damit verbundene Verwendung von komplexeren Mengensysteme wie der Borelschen σ-Algebra, andererseits kann dadurch auch auf die Verwendung von Integralen zugunsten der Verwendung von (endlichen oder unendlichen) Summen verzichtet werden.
Einfachstes Beispiel einer diskreten Wahrscheinlichkeitsverteilung wäre ein Wurf mit einer möglicherweise gezinkten Münze: Die Wahrscheinlichkeitsverteilung ordnet dem Ereignis "Die Münze zeigt Kopf" eine Zahl zu, die der Wahrscheinlichkeit entspricht, dass die Münze Kopf zeigt. Ebenso ordnet sie dem Ergebnis "Die Münze zeigt Zahl" eine Zahl zu, die der Wahrscheinlichkeit entspricht, dass die Münze Zahl zeigt. Dem intuitiven Verständnis von Wahrscheinlichkeit entsprechend summieren sich diese Zahlen zu eins auf.
Dieser Artikel behandelt Eigenschaften von diskreten Wahrscheinlichkeitsverteilungen, welche für ebendiese charakteristisch sind. Für die allgemeinen Eigenschaften von Wahrscheinlichkeitsmaßen, die auch für diskrete Wahrscheinlichkeitsverteilungen gelten; siehe den Hauptartikel zu den Wahrscheinlichkeitsmaßen.
Definition
Eine Wahrscheinlichkeitsverteilung heißt eine diskrete Wahrscheinlichkeitsverteilung, wenn einer der folgenden drei Fälle gilt:
- Sie ist auf einer endlichen
Menge definiert (meist
)
- Sie ist auf einer abzählbar
unendlichen Menge definiert (meist die natürlichen
Zahlen
)
- Sie ist auf einer beliebigen Menge definiert, nimmt aber nur auf höchstens
abzählbar vielen Elementen dieser Menge einen positiven Wert an. Das bedeutet
es existiert eine höchstens abzählbare Menge
mit
(meist die natürlichen Zahlen, eingebettet in die reellen Zahlen).
Zufallsvariablen, deren Verteilung eine diskrete Wahrscheinlichkeitsverteilung ist werden auch als diskrete Zufallsvariablen bezeichnet.
Beispiele
Beispiel für die Definition auf einer endlichen Menge ist das Eingangs
genannte Beispiel mit dem Münzwurf. Dieses wird auf der Menge
definiert und ist im fairen Fall gegeben durch
.
Häufig werden die Seiten der Münze auch kodiert, wie Kopf = 1, Zahl =0 oder Kopf = K, Zahl = Z. Die Kodierung ändert dabei nichts an der Eigenschaft der Verteilung, diskret zu sein.
Typisches Beispiel einer Wahrscheinlichkeitsverteilung auf einer abzählbar
unendlichen Menge, genauer auf
ist die Poisson-Verteilung.
Sie wird für einen reellen Parameter
definiert durch
.
Die Normiertheit einer Wahrscheinlichkeitsverteilung folgt hier aus der Definition der Exponentialfunktion über die Potenzreihe.
Beide obigen Beispiele können auch als diskrete
Wahrscheinlichkeitsverteilungen auf dem Grundraum
aufgefasst werden. Dies ermöglicht beispielsweise das definieren einer Verteilungsfunktion
und erlaubt die Faltung
der Wahrscheinlichkeitsverteilungen mit weiteren, eventuell stetigen
Wahrscheinlichkeitsverteilungen.
Konstruktion
Diskrete Wahrscheinlichkeitsverteilungen werden meist mittels Wahrscheinlichkeitsfunktionen
definiert. Im Falle des Grundraumes
sind dies Funktionen
,
die jeder natürlichen Zahl
eine positive, reelle Zahl zwischen null und eins zuordnet. Alle diese reellen
Zahlen müssen sich zu eins aufsummieren. Dann setzt man
.
Im obigen Beispiel der Poisson-Verteilung wäre zum Beispiel
.
Dieses Verfahren lässt sich für beliebige diskrete Wahrscheinlichkeitsverteilungen verwenden. Tatsächlich sind die diskreten Wahrscheinlichkeitsverteilungen genau diejenigen Verteilungen, die sich über eine Wahrscheinlichkeitsfunktion definieren lassen. Die Zuordnung diskrete Wahrscheinlichkeitsverteilung - Wahrscheinlichkeitsfunktion ist also bijektiv.
Eigenschaften
Verteilungsfunktion
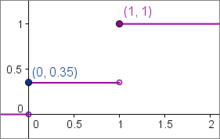
Bettet man diskrete Verteilungen auf
(oder einer beliebigen höchstens abzählbaren Teilmenge der reellen Zahlen) in
die reellen Zahlen
ein, so kann der Verteilung eine Verteilungsfunktion
zugeordnet werden. Diese zeichnet sich bei diskreten
Wahrscheinlichkeitsverteilungen dadurch aus, dass sie stückweise konstant ist.
An einer Stelle
mit
besitzt die Verteilungsfunktion immer einen „Sprung“ nach oben, und das um genau
den Wert
.
Wahrscheinlichkeitserzeugende Funktion
Diskreten Wahrscheinlichkeitsverteilungen auf
kann zusätzlich zu den klassischen erzeugenden Funktionen (Momenterzeugende
Funktion, Kumulantenerzeugende
Funktion und Charakteristische
Funktion) noch eine Wahrscheinlichkeitserzeugende
Funktion zuggeornet werden. Dabei handelt es sich um ein Polynom oder um eine Potenzreihe, die jeder
Wahrscheinlichkeitsverteilung eindeutig zugeordnet werden kann.
Wahrscheinlichkeitserzeugende Funktionen erleichtern Beispielsweise das
Berechnen der Momente
wie Erwartungswert oder Varianz oder liefern einfache Faltungsidenditäten.
Spezielle diskrete Wahrscheinlichkeitsverteilungen
Folgend sind einige wichtige diskrete Wahrscheinlichkeitsverteilungen und ihre Konstruktion aufgezählt. Die Einteilung ist dabei nicht zwingend, manche Verteilungen können auch auf mehrere Arten konstruiert werden.
Aus der Bernoulli-Verteilung abgeleitet
Ein Ausgangspunkt der Modellierung ist die Bernoulli-Verteilung.
Sie modelliert den Wurf einer Münze, wobei "Kopf" mit 1 codiert wird und "Zahl"
mit 0. Die Wahrscheinlichkeit für "Kopf" wird durch eine Zahl
gegeben. Somit handelt es sich um eine diskrete Wahrscheinlichkeitsverteilung
auf
.
Aus dieser Verteilung lassen sich direkt ableiten:
- Die Binomialverteilung: Sie gibt die Wahrscheinlichkeit an, bei n unabhängigen Würfen mit derselben Münze k Erfolge zu erhalten. Ihre multivariate Entsprechung ist die Multinomialverteilung.
- Die Verallgemeinerte Binomialverteilung: Sie gibt die Wahrscheinlichkeit an, bei n unabhängigen Würfen mit unterschiedlichen Münzen k Erfolge zu erhalten.
- Die Geometrische Verteilung: Sie gibt die Wahrscheinlichkeit für die Wartezeit auf den ersten Erfolg beim sukzessiven, unabhängigen Werfen einer Münze an.
- Die Negative Binomialverteilung: Sie gibt die Wahrscheinlichkeit für die Wartezeit auf den r.-ten Erfolg beim sukzessiven, unabhängigen Werfen einer Münze an.
Dabei werden geometrische und negative Binomialverteilung auch in verschiedenen Varianten definiert. Weitere ableitbare Wahrscheinlichkeitsverteilungen sind die Beta-Binomialverteilung (die Erfolgswahrscheinlichkeit der Münze selbst wird als Betaverteilt angenommen) sowie die Rademacher-Verteilung und die Zweipunktverteilung (Bernoulli-Verteilungen auf speziellen Werten) und die Dirac-Verteilung (degeneriertet Grenzfall einer Münze, die immer dasselbe Ergebnis zeigt).
Aus dem Urnenmodell abgeleitet
Ein weiterer Ausgangspunkt der Modellierung ist das Urnenmodell, das auf der
diskreten
Gleichverteilung basiert. Dabei werden insgesamt
Kugeln in mehrere Gruppen geteilt (gefärbt, nummeriert, etc.), in eine Urne
gelegt. Aus dieser wird dann gezogen, entweder mit zurücklegen oder ohne. Dabei
soll (entsprechend der Gleichverteilung) jede Kugel gleich wahrscheinlich sein.
So lassen sich beispielsweise konstruieren:
- die Hypergeometrische Verteilung: Sie gibt die Wahrscheinlichkeit an, bei n-maligem Ziehen ohne Zurücklegen aus einer Urne mit zwei Sorten Kugeln genau k Kugeln einer Sorte zu erhalten.
- ihr multivariates Pendant, die multivariate hypergeometrische Verteilung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.02. 2022