Wahrscheinlichkeitsfunktion

Wahrscheinlichkeitsfunktion eines fairen Würfels. Alle Augenzahlen haben die gleiche Wahrscheinlichkeit 1/6.

Eine Wahrscheinlichkeitsfunktion, auch Zähldichte genannt, ist eine spezielle reellwertige Funktion in der Stochastik. Wahrscheinlichkeitsfunktionen werden zur Konstruktion und Untersuchung von Wahrscheinlichkeitsverteilungen, genauer diskreten Wahrscheinlichkeitsverteilungen verwendet. Dabei kann jeder diskreten Wahrscheinlichkeitsverteilung eine eindeutige Wahrscheinlichkeitsfunktion zugeordnet werden. Umgekehrt definiert jede Wahrscheinlichkeitsfunktion eine eindeutig bestimmte diskrete Wahrscheinlichkeitsverteilung.

In den meisten Fällen werden Wahrscheinlichkeitsfunktionen auf den natürlichen Zahlen definiert. Sie ordnen dann jeder Zahl die Wahrscheinlichkeit zu, dass diese Zahl auftritt. So würde bei der Modellierung eines fairen Würfels die Wahrscheinlichkeitsfunktion den Zahlen von eins bis sechs jeweils den Wert ${\tfrac {1}{6}}$ zuordnen und allen anderen die null.

Aus der Sicht der Maßtheorie handelt es sich bei Wahrscheinlichkeitsfunktionen um spezielle Dichtefunktionen (im Sinne der Maßtheorie) bezüglich des Zählmaßes. Diese werden im allgemeineren Kontext auch Gewichtsfunktionen genannt.

Definition

Definition Wahrscheinlichkeitsfunktion: Für eine diskrete Zufallsvariable ist die Wahrscheinlichkeitsfunktion f(x) für $x\in \mathbb {R}$ definiert durch

$f(x)={\begin{cases}P(X=x_{i})=p_{i},&x=x_{i}\in \{x_{1},x_{2},\dots ,x_{k}\dots \}\\0,&{\text{ sonst.}}\end{cases}}$

Zur Konstruktion von Wahrscheinlichkeitsverteilungen

Gegeben sei eine Funktion

$f\colon \mathbb {N} \to \mathbb {R}$ ,

für die gilt

Es ist $f(i)\in [0,1]$ für alle $i\in \mathbb{N}$ . ordnet also jeder natürlichen Zahl eine reelle Zahl zwischen null und eins zu.
ist normiert in dem Sinne, dass sich die Funktionswerte zu eins aufsummieren. Es gilt also

$\sum _{i=0}^{\infty }f(i)=1$ .

Dann heißt eine Wahrscheinlichkeitsfunktion und definiert durch

$P(\{i\}):=f(i)$ für alle $i\in \mathbb{N}$

eine eindeutig bestimmte Wahrscheinlichkeitsverteilung auf den natürlichen Zahlen $\mathbb{N}$ , versehen mit der Potenzmenge ${\mathcal {P}}(\mathbb {N} )$ als Ereignissystem.

Aus Wahrscheinlichkeitsverteilungen abgeleitet

Gegeben sei eine Wahrscheinlichkeitsverteilung auf den natürlichen Zahlen $\mathbb{N}$ , versehen mit ${\mathcal {P}}(\mathbb {N} )$ , und sei eine Zufallsvariable mit Werten in $\mathbb{N}$ . Dann heißt

$f_{P}\colon \mathbb {N} \to \mathbb {R}$

definiert durch

$f_{P}(i):=P(\{i\})$

die Wahrscheinlichkeitsfunktion von . Analog heißt

$f_{X}\colon \mathbb {N} \to \mathbb {R}$

definiert durch

$f_{X}(i):=P(X=i)$

die Wahrscheinlichkeitsfunktion von

Beispiele

Eine typische Wahrscheinlichkeitsfunktion ist

$f_{n,p}(k)={\begin{cases}{\binom {n}{k}}p^{k}(1-p)^{n-k}&{\text{ für }}k\in \{0,1,\dots ,n\}\\0&{\text{ sonst}}\end{cases}}$

für eine natürliche Zahl und eine reelle Zahl $p\in (0,1)$ . Die Normiertheit folgt hier direkt aus dem binomischen Lehrsatz, denn es ist

$\sum _{k=0}^{\infty }f_{n,p}(k)=\sum _{k=0}^{n}{\binom {n}{k}}p^{k}(1-p)^{n-k}=((1-p)+p)^{n}=1$ .

Die so erzeugte Wahrscheinlichkeitsverteilung ist die Binomialverteilung.

Eine weitere klassische Wahrscheinlichkeitsfunktion ist

$f_{p}(k)=p(1-p)^{k}$ für $k\in \{0,1,2,\dots \}$

und ein $p\in (0,1)$ . Hier folgt die Normiertheit aus der geometrischen Reihe, denn es ist

$\sum _{k=0}^{\infty }f_{p}(k)=p\sum _{k=0}^{\infty }(1-p)^{k}={\frac {p}{1-(1-p)}}=1$ .

Die so erzeugte Wahrscheinlichkeitsverteilung ist die Geometrische Verteilung.

Allgemeine Definition

Die Definition lässt sich von den natürlichen Zahlen auf beliebige höchstens abzählbare Mengen ausweiten. Ist $\Omega$ solch eine Menge und ist

$f\colon \Omega \to [0,1]$

mit

$\sum _{i\in \Omega }f(i)=1$ ,

so definiert durch

$P(\{i\}):=f(i)$ für alle $i\in \Omega$

eine eindeutig bestimmte Wahrscheinlichkeitsverteilung auf $(\Omega ,{\mathcal {P}}(\Omega ))$ . Ist umgekehrt eine Wahrscheinlichkeitsverteilung auf $(\Omega ,{\mathcal {P}}(\Omega ))$ und eine Zufallsvariable mit Werten in $\Omega$ , so heißen

$f_{P}\colon \Omega \to [0,1]$ definiert durch $f_{P}(i):=P(\{i\})$

und

$f_{X}\colon \Omega \to [0,1]$ definiert durch $f_{X}(i):=P(X=i)$

die Wahrscheinlichkeitsfunktion von beziehungsweise .

Alternative Definition

Manche Autoren definieren zuerst reelle Folgen $(p_{i})_{i\in \Omega }$ mit $p_{i}\in [0,1]$ für alle $i\in \Omega$ und

$\sum _{i\in \Omega }p_{i}=1$

und nennen diese Folgen Wahrscheinlichkeitsvektoren oder stochastische Folgen.

Eine Wahrscheinlichkeitsfunktion wird dann definiert als

$f\colon \Omega \to [0,1]$

gegeben durch

$f(i)=p_{i}$ für alle $i\in \Omega$

Umgekehrt definiert dann jede Wahrscheinlichkeitsverteilung oder Zufallsvariable auf $\Omega$ auch eine stochastische Folge/Wahrscheinlichkeitsvektor über $(P(\{i\}))_{i\in \Omega }$ beziehungsweise $(P(X=i))_{i\in \Omega }$

Andere Autoren nennen bereits die Folge $(p_{i})_{i\in \Omega }$ eine Zähldichte.

Weitere Beispiele

Typisches Beispiel für Wahrscheinlichkeitsfunktionen auf beliebigen Mengen ist die diskrete Gleichverteilung auf einer endlichen Menge $\Omega$ . Sie besitzt dann per Definition die Wahrscheinlichkeitsfunktion

$f(i)={\tfrac {1}{|\Omega |}}$ für alle $i\in \Omega$ .

Der Zugang über die stochastischen Folgen erlaubt die folgende Konstruktion von Wahrscheinlichkeitsfunktionen: Ist eine beliebige (höchstens abzählbare) Folge von positiven reellen Zahlen $(a_{i})_{i\in \Omega }$ mit Indexmenge $\Omega$ gegeben, für die

$\sum _{i\in \Omega }a_{i}<\infty$

gilt, so definiert man

$c=\sum _{i\in \Omega }a_{i}$ .

Dann ist $({\tfrac {a_{i}}{c}})_{i\in \Omega }$ eine stochastische Folge und definiert damit auch eine Wahrscheinlichkeitsfunktion. Betrachtet man zum Beispiel die Folge

$a_{k}:={\frac {\lambda ^{k}}{k!}}$ für $k\in \mathbb {N}$ ,

so ist

$\sum _{k=0}^{\infty }{\frac {\lambda ^{k}}{k!}}=e^{\lambda }$ .

Somit ist die Normierungskonstante $c=e^{\lambda }$ und als Wahrscheinlichkeitsfunktion ergibt sich

$f(k)=e^{-\lambda }{\frac {\lambda ^{k}}{k!}}$ .

Dies ist die Wahrscheinlichkeitsfunktion der Poisson-Verteilung.

Bestimmung von Kennzahlen durch Wahrscheinlichkeitsfunktionen

Viele der wichtigen Kennzahlen von Zufallsvariablen und Wahrscheinlichkeitsverteilungen lassen sich bei Existenz der Wahrscheinlichkeitsfunktion direkt aus dieser herleiten.

Erwartungswert

Ist eine Zufallsvariable mit Werten in $\mathbb{N}$ und Wahrscheinlichkeitsfunktion $f_{X}$ , so ist der Erwartungswert gegeben durch

$\operatorname {E} (X)=\sum _{k=0}^{\infty }k\cdot f_{X}(k)$ .

Er existiert immer, kann aber auch unendlich sein. Ist allgemeiner $\Omega \subset \mathbb {R}$ eine höchstens abzählbare Teilmenge der reellen Zahlen und eine Zufallsvariable mit Werten in und Wahrscheinlichkeitsfunktion $f_{X}$ so ist der Erwartungswert gegeben durch

$\operatorname {E} (X)=\sum _{k\in \Omega }k\cdot f_{X}(k)$

falls die Summe existiert.

Varianz

Analog zum Erwartungswert lässt sich auch die Varianz direkt aus der Wahrscheinlichkeitsfunktion herleiten. Sei dazu

$\operatorname {E} (X)=\mu$

der Erwartungswert. Ist dann eine Zufallsvariable mit Werten in $\mathbb{N}$ und Wahrscheinlichkeitsfunktion $f_{X}$ , so ist die Varianz gegeben durch

$\operatorname {Var} (X)=\sum _{k=0}^{\infty }(k-\mu )^{2}f_{X}(k)$

oder aufgrund des Verschiebungssatzes äquivalent dazu

$\operatorname {Var} (X)=-\mu ^{2}+\sum _{k=0}^{\infty }k^{2}f_{X}(k)$

Entsprechend gilt im allgemeineren Fall einer Zufallsvariable mit Werten in $\Omega$ (vgl. oben), dass

$\operatorname {Var} (X)=\sum _{k\in \Omega }(k-\mu )^{2}f_{X}(k)$

Auch hier gelten alle Aussagen nur, wenn die entsprechenden Summen existieren.

Modus

Für diskrete Wahrscheinlichkeitsverteilungen wird der Modus direkt über die Wahrscheinlichkeitsfunktion definiert: Ist eine Zufallsvariable mit Werten in $\mathbb{N}$ und Wahrscheinlichkeitsfunktion oder ist eine Wahrscheinlichkeitsverteilung auf $\mathbb{N}$ mit Wahrscheinlichkeitsfunktion , so heißt $k_{\text{mod}}$ ein Modus oder Modalwert von oder , wenn

$f(k-1)\leq f(k_{\text{mod}})\geq f(k+1)$

ist. Ist etwas allgemeiner eine höchstens abzählbare Menge $\Omega$ gegeben, deren Elemente $x_{k}$ in aufsteigender Ordnung sortiert sind, das heißt $\dots <x_{k-1}<x_{k}<x_{k+1}<\dots$ , so heißt ein $x_{k}$ ein Modus oder Modalwert, wenn

$f(x_{k-1})\leq f(x_{k})\geq f(x_{k+1})$

gilt.

Eigenschaften und aufbauende Begriffe

Verteilungsfunktionen und Wahrscheinlichkeitsfunktionen

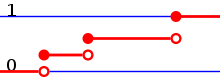
Verteilungsfunktion eines Wahrscheinlichkeitsmaßes, dass sich über eine Wahrscheinlichkeitsfunktion definieren lässt. Charakteristischerweise hat die Verteilungsfunktion an der Stelle

einen Sprung um $f(i)=P(\{i\})$ nach oben.

Ist eine Wahrscheinlichkeitsfunktion auf $\mathbb{N}$ , so ist die Verteilungsfunktion des entsprechenden Wahrscheinlichkeitsmaßes gegeben als

$F_{P}(x)=\sum _{i=0}^{\lfloor x\rfloor }f(i)$ .

Dabei bezeichnet $\lfloor \cdot \rfloor$ die Abrundungsfunktion, das heißt $\lfloor x\rfloor$ ist größte ganze Zahl, die kleiner oder gleich ist.

Ist auf einer höchstens abzählbaren Teilmenge der reellen Zahlen definiert, also auf $A \subset \R$ , so ist die Verteilungsfunktion des Wahrscheinlichkeitsmaßes definiert durch

$F_{P}(x)=\sum _{i\leq x}f(i)$ .

Beispiel hierfür ist $A=\mathbb {Z}$ .

Faltung und Summe von Zufallsvariablen

Für Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsfunktionen kann die Faltung (von Wahrscheinlichkeitsverteilungen) auf die Faltung (von Funktionen) der entsprechenden Wahrscheinlichkeitsfunktionen zurückgeführt werden. Sind $P,Q$ Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsfunktionen f_P und $f_{Q}$ , so ist

$f_{P*Q}=f_{P}*f_{Q}$ .

Hierbei bezeichnet $P*Q$ die Faltung von und und $f*g$ die Faltung der Funktionen und . Die Wahrscheinlichkeitsfunktion der Faltung zweier Wahrscheinlichkeitsverteilungen ist somit genau die Faltung der Wahrscheinlichkeitsfunktionen der Wahrscheinlichkeitsverteilungen.

Diese Eigenschaft überträgt sich direkt auf die Summe von stochastisch unabhängigen Zufallsvariablen. Sind zwei stochastisch unabhängige Zufallsvariablen $X,Y$ mit Wahrscheinlichkeitsfunktionen $f_{X}$ und $f_{Y}$ gegeben, so ist

$f_{X+Y}=f_{X}*f_{Y}$ .

Die Wahrscheinlichkeitsfunktion der Summe ist somit die Faltung der Wahrscheinlichkeitsfunktionen der einzelnen Zufallsvariablen.

Wahrscheinlichkeitserzeugende Funktion

→ Hauptartikel: Wahrscheinlichkeitserzeugende Funktion

Auf $\mathbb{N}$ lässt sich jeder Wahrscheinlichkeitsverteilung eine wahrscheinlichkeitserzeugende Funktion zuordnen. Dies ist ein Polynom oder eine Potenzreihe mit der Wahrscheinlichkeitsfunktion als Koeffizienten. Sie ist somit definiert als

$m_{P}(t)=\sum _{k=0}^{\infty }f_{P}(k)t^{k}$

für die Wahrscheinlichkeitsfunktion f_P einer Wahrscheinlichkeitsverteilung . Die wahrscheinlichkeitserzeugende Funktion einer Zufallsvariable wird analog definiert.

Wahrscheinlichkeitserzeugende Funktionen erleichtern die Untersuchung von und das Rechnen mit Wahrscheinlichkeitsverteilungen. So ist beispielsweise die wahrscheinlichkeitserzeugende Funktion der Faltung zweier Wahrscheinlichkeitsverteilungen genau das Produkt der wahrscheinlichkeitserzeugenden Funktionen der einzelnen Wahrscheinlichkeitsverteilungen. Ebenso finden sich wichtige Kennzahlen wie der Erwartungswert und die Varianz in den Ableitungen der wahrscheinlichkeitserzeugenden Funktionen wieder.

Basierend auf einem Artikel in:

Wikipedia.de