Lineare Einfachregression
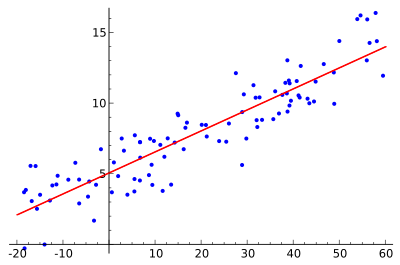
In der Statistik ist die lineare Einfachregression, oder auch einfache lineare Regression (kurz: ELR, selten univariate lineare Regression) genannt, ein regressionsanalytisches Verfahren und ein Spezialfall der linearen Regression. Die Bezeichnung einfach gibt an, dass bei der linearen Einfachregression nur eine unabhängige Variable verwendet wird, um die Zielgröße zu erklären. Ziel ist die Schätzung von Achsenabschnitt und Steigung der Regressionsgeraden sowie die Schätzung der Varianz der Störgrößen.
Einführung in die Problemstellung
Das Ziel einer Regression ist es, eine abhängige Variable durch eine oder
mehrere unabhängige Variablen zu erklären. Bei der einfachen linearen Regression
wird eine abhängige Variable lediglich durch eine unabhängige
Variable erklärt. Das Modell der linearen Einfachregression geht daher von
zwei metrischen Größen aus: einer Einflussgröße
(auch: erklärende Variable, Regressor oder unabhängige Variable) und einer
Zielgröße
(auch: endogene
Variable, abhängige Variable, erklärte Variable oder Regressand). Des
Weiteren liegen
Paare
von Messwerten vor (die Darstellung der Messwerte
im
-
-Diagramm
wird im Folgenden Streudiagramm
bezeichnet), die in einem funktionalen
Zusammenhang stehen, der sich aus einem systematischen und einem stochastischen Teil
zusammensetzt:
Die stochastische Komponente beschreibt nur noch zufällige Einflüsse
(z.B. zufällige
Abweichungen wie Messfehler),
alle systematischen Einflüsse sind in der systematischen Komponente enthalten.
Die lineare Einfachregression stellt den Zusammenhang zwischen der Einfluss- und
der Zielgröße mithilfe von zwei festen, unbekannten, reellen Parametern
und
auf lineare Weise her, d.h. die Regressionsfunktion
wird wie folgt spezifiziert:
Dadurch ergibt sich das Modell der linearen Einfachregression wie folgt:
.
Hierbei ist
die abhängige Variable und stellt eine Zufallsvariable
dar. Die
-Werte
sind beobachtbare, nicht zufällige Messwerte, der bekannten erklärenden
Variablen
;
die Parameter
und
sind unbekannte skalare
Regressionsparameter und
ist eine zufällige und unbeobachtbare Störgröße. Bei der einfachen linearen
Regression wird also eine Gerade so durch das Streudiagramm gelegt, dass der
lineare Zusammenhang zwischen
und
möglichst gut beschrieben wird.
Einführendes Beispiel
Eine renommierte Sektkellerei möchte einen hochwertigen Rieslingsekt auf den
Markt bringen. Für die Festlegung des Abgabepreises
soll zunächst eine Preis-Absatz-Funktion
ermittelt werden. Dazu wird in
Geschäften ein Testverkauf durchgeführt und man erhält sechs Wertepaare mit dem
jeweiligen Ladenpreis einer Flasche
(in Euro) sowie der Zahl der jeweils verkauften Flaschen
:
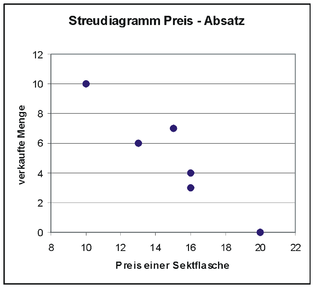
| Geschäft |
1 | 2 | 3 | 4 | 5 | 6 |
| Flaschenpreis |
20 | 16 | 15 | 16 | 13 | 10 |
| verkaufte Menge |
0 | 3 | 7 | 4 | 6 | 10 |
| Geschätzte Regressionskoeffizienten | |
|---|---|
|
| |
| Verwendete Symbole | |
| Mittel der Messwerte | |
| Messwerte | |
Auf die Vermutung, dass es sich um einen linearen Zusammenhang handelt, kommt man, wenn man das obige Streudiagramm betrachtet. Dort erkennt man, dass die eingetragenen Datenpunkte nahezu auf einer Linie liegen. Im Weiteren sind der Preis als unabhängige und die Zahl der verkauften Flaschen als abhängige Variable definiert und es gibt sechs Beobachtungen. Die Anzahl der verkauften Flaschen mag aber nicht nur vom Preis abhängen, z.B. könnte in der Verkaufsstelle 3 eine große Werbetafel gehangen haben, so dass dort mehr Flaschen als erwartet verkauft wurden (zufälliger Einfluss). Damit scheint das einfache lineare Regressionsmodell zu passen.
Nach der graphischen Inspektion, ob ein linearer Zusammenhang vorliegt, wird zunächst die Regressiongerade mit der Methode der kleinsten Quadrate geschätzt und es ergeben sich die Formeln in der Infobox für die geschätzten Regressionsparameter.
Für das folgende Zahlenbeispiel ergeben sich für die abhängige und
unabhängige Variable jeweils ein Mittelwert
zu
und
.
Somit erhält man die Schätzwerte
für
und
für
durch einfaches Einsetzen in die weiter unten erklärten Formeln. Zwischenwerte
(z.B.
)
in diesen Formeln sind in folgender Tabelle dargestellt
| Flaschenpreis |
verkaufte Menge |
|||||||||
| 1 | 20 | 0 | 5 | −5 | −25 | 25 | 25 | 0,09 | −0,09 | 0,0081 |
| 2 | 16 | 3 | 1 | −2 | −2 | 1 | 4 | 4,02 | −1,02 | 1,0404 |
| 3 | 15 | 7 | 0 | 2 | 0 | 0 | 4 | 5,00 | 2,00 | 4,0000 |
| 4 | 16 | 4 | 1 | −1 | −1 | 1 | 1 | 4,02 | −0,02 | 0,0004 |
| 5 | 13 | 6 | −2 | 1 | −2 | 4 | 1 | 6,96 | −0,96 | 0,9216 |
| 6 | 10 | 10 | −5 | 5 | −25 | 25 | 25 | 9,91 | 0,09 | 0,0081 |
| Summe | 90 | 30 | 0 | 0 | −55 | 56 | 60 | 30,00 | 0,00 | 5,9786 |
Es ergibt sich in dem Beispiel
und
.
Die geschätzte Regressionsgerade lautet somit
,
sodass man vermuten kann, dass bei jedem Euro mehr der Absatz im Mittel um ungefähr eine Flasche sinkt.
Für einen konkreten Preis
kann die Absatzmenge ausgerechnet werden, z.B.
ergibt sich eine geschätzte Absatzmenge von
.
Für jeden Beobachtungswert
kann eine geschätzte Absatzmenge angegeben werden, z.B. für
ergibt sich
.
Die geschätzte Störgröße, genannt Residuum,
ist dann
.
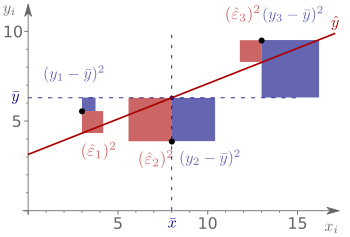
Bestimmtheitsmaß
.png)
Das Bestimmtheitsmaß
misst, wie gut die Messwerte zu einem Regressionsmodell passen (Anpassungsgüte). Es
ist definiert als der Anteil der „erklärten
Variation“ an der „Gesamtvariation“
und liegt daher zwischen:
(oder
): kein linearer Zusammenhang und
(oder
): perfekter linearer Zusammenhang.
Je näher das Bestimmtheitsmaß am Wert Eins liegt, desto höher ist die
„Bestimmtheit“ bzw. „Güte“ der Anpassung. Ist ,
dann besteht das „beste“ lineare
Regressionsmodell nur aus dem Achsenabschnitt
,
während
ist. Je näher der Wert des Bestimmtheitsmaß an
liegt, desto besser erklärt die Regressionsgerade das wahre Modell. Ist
,
dann lässt sich die abhängige Variable
vollständig durch das lineare Regressionsmodell erklären. Anschaulich liegen
dann die Messpunkte
alle auf der nichthorizontalen Regressionsgeraden. Somit liegt bei diesem Fall
kein stochastischer Zusammenhang vor, sondern ein deterministischer.
Eine häufige Fehlinterpretation eines niedrigen Bestimmtheitsmaßes ist es,
dass es keinen Zusammenhang zwischen den Variablen gibt. Tatsächlich wird nur
der lineare Zusammenhang gemessen, d.h. obwohl
klein ist, kann es trotzdem einen starken nichtlinearen Zusammenhang geben.
Umgekehrt muss ein hoher Wert des Bestimmtheitsmaßes nicht bedeuten, dass ein
nichtlineares Regressionsmodell nicht noch besser als ein lineares Modell ist.
Bei einer einfachen linearen Regression entspricht das Bestimmtheitsmaß
dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten
(siehe Bestimmtheitsmaß
als quadrierter Korrelationskoeffizient).
Im oben genannten Beispiel kann die Güte des Regressionsmodells mit Hilfe des Bestimmtheitsmaßes überprüft werden. Für das Beispiel ergibt sich für die Residuenquadratsumme und die totale Quadratsumme
und
und das Bestimmtheitsmaß zu
.
Das heißt ca. 90 % der Variation bzw. Streuung in
können mithilfe des Regressionsmodells „erklärt“ werden, nur 10 % der
Streuung bleiben „unerklärt“.
Das Modell
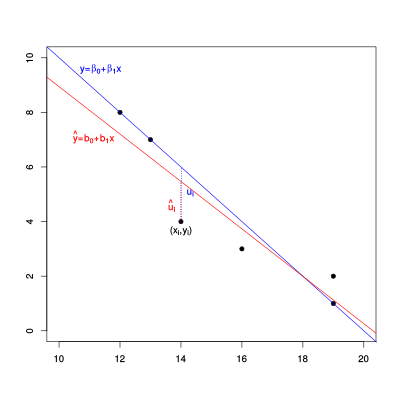
Im Regressionsmodell werden die Zufallskomponenten mit Hilfe von Zufallsvariablen
modelliert. Wenn
eine Zufallsvariable ist, dann ist es auch
.
Die beobachteten Werte
werden als Realisierungen
der Zufallsvariablen
aufgefasst.
Daraus ergibt sich das einfache lineare Regressionsmodell:
(mit Zufallsvariablen) bzw.
(mit deren Realisierungen).
Bildlich gesprochen wird eine Gerade
durch das Streudiagramm
der Messung gelegt. In der gängigen Literatur wird die Gerade oft durch den Achsenabschnitt
und den Steigungsparameter
beschrieben. Die abhängige Variable wird in diesem Kontext oft auch endogene
Variable genannt. Dabei ist
eine additive stochastische Störgröße, die Abweichungen vom idealen Zusammenhang
– also der Geraden – achsenparallel misst.
Anhand der Messwerte
werden die Regressionsparameter
und die
geschätzt. So erhält man die
Stichproben-Regressionsfunktion
.
Im Gegensatz zur unabhängigen und abhängigen Variablen sind die
Zufallskomponenten
und deren Realisierungen nicht direkt beobachtbar. Ihre geschätzten
Realisierungen
sind nur indirekt beobachtbar und heißen Residuen.
Sie sind berechnete Größen und messen den vertikalen Abstand zwischen
Beobachtungspunkt und der geschätzten Regressionsgerade
Modellannahmen
Um die Zerlegung von
in eine systematische und zufällige Komponente zu sichern sowie gute
Schätzeigenschaften für die Schätzung
und
der Regressionsparameter
und
zu haben, sind einige Annahmen bezüglich der Störgrößen sowie der unabhängigen
Variable nötig.
Annahmen über die unabhängige Variable
In Bezug auf die unabhängige Variable werden folgende Annahmen getroffen:
- Die Werte der unabhängigen Variablen
sind deterministisch, d. h. sie sind fest gegeben
- Sie können also wie in einem Experiment kontrolliert werden und sind damit
keine Zufallsvariablen (Exogenität
der Regressoren). Wären die
Zufallsvariablen, z.B. wenn die
auch nur fehlerbehaftet gemessen werden können, dann wäre
und die Verteilung von
sowie die Verteilungsparameter (Erwartungswert und Varianz) würden nicht nur von
abhängen
.
- Mit speziellen Regressionsverfahren kann dieser Fall aber auch behandelt werden, siehe z.B. Regression mit stochastischen Regressoren.
- Stichprobenvariation in der unabhängigen Variablen
- Die Realisierungen der unabhängigen Variablen
sind nicht alle gleich. Man schließt also den unwahrscheinlichen Fall aus, dass die unabhängige Variable keinerlei Variabilität aufweist, d.h.
. Dies impliziert, dass die Quadratsumme der unabhängigen Variablen
positiv sein muss. Diese Annahme wird im Schätzprozess benötigt.
- Keine perfekte Multikollinearität
- Dies bedeutet, dass sich keine unabhängige Variable als eine perfekte Linearkombination aus den anderen unabhängigen Variablen ergeben darf.
Annahmen über die unabhängige und abhängige Variable
- Der wahre Zusammenhang zwischen den Variablen
und
ist linear
- Die Regressionsgleichung der einfachen linearen Regression muss linear in
den Parametern
und
sein, kann aber nichtlineare Transformationen der unabhängigen und der abhängigen Variablen beinhalten. Beispielsweise sind die Transformationen
und
zulässig, da sie ebenfalls lineare Modelle darstellen. Bei transformierten Daten ist zu beachten, dass sie die Interpretation der Regressionsparameter ändert.
- Vorliegen einer Zufallsstichprobe
Es liegt eine Zufallsstichprobe
des Umfangs
mit Realisierungen
vor, die dem wahren Modell
Annahmen über die Störgrößen
In Bezug auf die Störgrößen werden folgende Annahmen getroffen:
- Der Erwartungswert der Störgrößen ist Null:
- Wenn das Modell einen – von Null verschiedenen – Achsenabschnitt enthält,
ist es vernünftig dass man zumindest fordert dass der Mittelwert von
in der Grundgesamtheit Null ist und sich die Schwankungen der einzelnen Störgrößen über die Gesamtheit der Beobachtungen ausgleichen. Mathematisch bedeutet das, dass der Erwartungswert der Störgrößen Null ist
. Diese Annahme macht keine Aussage über den Zusammenhang zwischen
und
, sondern gibt lediglich eine Aussage über die Verteilung der unsystematischen Komponente in der Grundgesamtheit. Dies bedeutet, dass das betrachte Modell im Mittel dem wahren Zusammenhang entspricht. Wäre der Erwartungswert nicht Null, dann würde man im Mittel einen falschen Zusammenhang schätzen. Zur Verletzung dieser Annahme kann es kommen, wenn eine relevante Variable im Regressionsmodell nicht berücksichtigt wurde (siehe Verzerrung durch ausgelassene Variablen).
- Die Störgrößen
sind voneinander unabhängige Zufallsvariablen
- Wären die Störgrößen nicht unabhängig, dann könnte man einen
systematischen Zusammenhang zwischen ihnen formulieren. Das würde der
Zerlegung von
in eine eindeutige systematische und zufällige Komponente widersprechen. Es wird in der Zeitreihenanalyse z.B. oft ein Zusammenhang der Form
betrachtet.
- Oft wird auch nur die Unkorreliertheit der
Störgrößen gefordert:
oder äquivalent
.
Unabhängige Zufallsvariablen sind immer auch unkorreliert. Man spricht in diesem Zusammenhang auch von Abwesenheit von Autokorrelation.
- Eine konstante Varianz
(Homoskedastizität)
der Störgrößen:
- Wäre die Varianz nicht konstant, liesse sich evtl. die Varianz
systematisch modellieren, d.h. dies widerspräche Zerlegung von
in eine eindeutige systematische und zufällige Komponente. Zudem lässt sich zeigen, dass sich die Schätzeigenschaften der Regressionsparameter verbessern lassen, wenn die Varianz nicht konstant ist.
Alle oben genannten Annahmen über die Störgrößen lassen sich so zusammenfassen:
,
d.h. alle Störgrößen sind unabhängig
und identisch verteilt mit Erwartungswert
und
.
- Optionale Annahme: Die Störgrößen sind normalverteilt,
also
- Diese Annahme wird nur benötigt um z.B. Konfidenzintervalle zu berechnen bzw. um Tests für die Regressionsparameter durchzuführen.
Wird die Normalverteilung der Störgrößen angenommen, so folgt, dass auch
normalverteilt ist:
Die Verteilung der
hängt also von der Verteilung der Störgrößen ab. Der Erwartungswert der
abhängigen Variablen lautet:
Da die einzige zufällige Komponente in
die Störgröße
ist, gilt für die Varianz der abhängigen Variablen, dass sie gleich der Varianz
der Störgrößen entspricht:
.
Die Varianz der Störgrößen spiegelt somit die Variabilität der abhängigen Variablen um ihren Mittelwert wider. Damit ergibt sich für die Verteilung der abhängigen Variablen:
.
Aufgrund der Annahme, dass die Störgrößen im Mittel Null sein müssen, muss
der Erwartungswert von
der Regressionsfunktion der Grundgesamtheit
entsprechen. D.h. mit der Annahme über die Störgrößen schlussfolgert man, dass das Modell im Mittel korrekt sein muss. Wenn zusätzlich zu den anderen Annahmen auch die Annahme der Normalverteiltheit gefordert wird spricht man auch vom klassischen linearen Modell (siehe auch #Klassisches lineares Modell der Normalregression).
Im Rahmen der Regressionsdiagnostik sollen die Voraussetzungen des Regressionsmodells, soweit möglich, geprüft werden. Dazu zählen die Überprüfung, ob die Störgrößen keine Struktur (die dann nicht zufällig wäre) haben.
Schätzung der Regressionsparameter und der Störgrößen
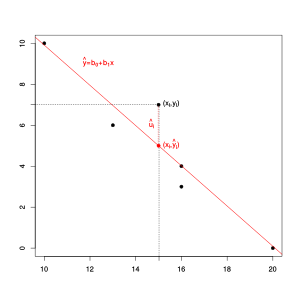
Die Schätzung der Regressionsparameter
und
und der Störgrößen
geschieht in zwei Schritten:
- Zunächst werden mit Hilfe der Kleinste-Quadrate-Schätzung
die unbekannten Regressionsparameter
und
geschätzt. Dabei wird die Summe der quadrierten Abweichungen zwischen dem geschätzten Regressionswert
und dem beobachteten Wert
minimiert. Dabei ergeben sich folgende Formeln:
- Sind
und
berechnet, so kann das Residuum geschätzt werden als
.
Herleitung der Formeln für die Regressionsparameter
Um nun die Parameter der Gerade zu bestimmen, wird die Zielfunktion
(Fehlerquadratsumme
bzw. die Residuenquadratsumme)
minimiert
Die Bedingungen erster Ordnung (notwendige Bedingungen) lauten:
und
.
Durch Nullsetzen der partiellen
Ableitungen nach
und
ergeben sich die gesuchten Parameterschätzer,
bei denen die Residuenquadratsumme
minimal wird:
und
,
wobei
die Summe
der Abweichungsprodukte zwischen
und
und
die Summe
der Abweichungsquadrate von
darstellt. Mithilfe des Verschiebungssatzes
von Steiner lässt sich
auch wie folgt einfacher, in nichtzentrierter
Form, darstellen
.
Weitere Darstellungen von
erhält man, indem man die Formel in Abhängigkeit des Bravais-Pearson-Korrelationskoeffizienten
schreibt. Entweder als
oder
,
wobei
und
die empirischen
Standardabweichungen von
und
darstellen. Die letztere Darstellung impliziert, dass der
Kleinste-Quadrate-Schätzer für den Anstieg proportional
zum Bravais-Pearson-Korrelationskoeffizienten
ist, d.h.
.
Die jeweiligen Kleinste-Quadrate-Schätzwerte von
und
werden als
und
abgekürzt.
Algebraische Eigenschaften der Kleinste-Quadrate-Schätzer
Aus den Formeln sind drei Eigenschaften ableitbar:
1.) Die Regressiongerade verläuft durch den Schwerpunkt bzw. durch das
„Gravitationszentrum“ der Daten ,
was direkt aus der obigen Definition von
folgt. Man sollte beachten, dass dies nur gilt, wenn ein Achsenabschnitt für die
Regression verwendet wird, wie man leicht an dem Beispiel mit den zwei
Datenpunkten
sieht.
2.) Die KQ-Regressionsgerade wird so bestimmt, dass die Residuenquadratsumme zu einem Minimum wird. Äquivalent dazu bedeutet das, dass sich positive und negative Abweichungen von der Regressionsgeraden ausgleichen. Wenn das Modell der linearen Einfachregression einen – von Null verschiedenen – Achsenabschnitt enthält, dann muss also gelten, dass die Summe der Residuen ist Null ist (dies ist äquivalent zu der Eigenschaft, dass die gemittelten Residuen Null ergeben)
bzw.
.
- Oder, da sich die Residuen
als Funktion der Störgrößen darstellen lassen
. Diese Darstellung wird für die Herleitung der erwartungstreuen Schätzung der Varianz der Störgrößen benötigt.
3.) Die Residuen und die unabhängigen Variablen sind (unabhängig davon ob ein Achsenabschnitt mit einbezogen wurde oder nicht) unkorreliert, d.h.
, was direkt aus der zweiten Optimalitätsbedingung von oben folgt.
- Die Residuen und die geschätzten Werten sind unkorreliert, d.h.
.
- Diese Unkorreliertheit der prognostizierten Werte mit den Residuen kann so interpretiert werden, dass in der Vorhersage bereits alle relevante Information der erklärenden Variablen bezüglich der abhängigen Variablen steckt.
Schätzfunktionen der Kleinste-Quadrate-Schätzer
Aus der Regressionsgleichung
lassen sich die Schätzfunktionen
für
und
für
ableiten.
mit der Gewichtsfunktion
.
Die Formeln zeigen auch, dass die Schätzfunktionen der Regressionsparameter
linear von
abhängen. Unter der Annahme der Normalverteilung der Residuen
(oder wenn für
der zentrale
Grenzwertsatz erfüllt ist) folgt, dass auch die Schätzfunktionen der
Regressionsparameter
und
zumindest approximativ normalverteilt sind:
und
.
Statistische Eigenschaften der Kleinste-Quadrate-Schätzer
Erwartungstreue der Kleinste-Quadrate-Schätzer
Die Schätzfunktionen der Regressionsparameter
und
sind erwartungstreu
für
und
,
d.h. es gilt
und
.
Der Kleinste-Quadrate-Schätzer liefert also „im Mittel“ die
wahren Werte der Koeffizienten.
Mit der Linearität des Erwartungswerts und der Voraussetzung
folgt nämlich
und :
.
Als Erwartungswert von
ergibt sich daher:
Für den Erwartungswert von
erhält man schließlich:
.
Varianzen der Kleinste-Quadrate-Schätzer
Die Varianzen des Achsenabschnittes
und des Steigungsparameters
sind gegeben durch:
und
.
Dabei stellt
die empirische
Varianz dar. Je größer die Streuung in der erklärenden Variablen (d.h.
je größer
),
desto größer ist die Präzision von
und
.
Da die Anzahl der Terme in dem Ausdruck
,
umso größer ist, je größer die Stichprobengröße
ist, führen größere Stichproben immer zu einer größeren Präzision. Außerdem kann
man sehen, dass je kleiner die Varianz der Störgrößen
ist, desto Präziser sind die Schätzer.
Die Kovarianz von
und
ist gegeben durch
.
Falls für
die Konsistenzbedingung
gilt, sind die Kleinste-Quadrate-Schätzer
und
konsistent
für
und
.
Dies bedeutet, dass mit zunehmender Stichprobengröße der wahre Wert immer
genauer geschätzt wird und die Varianz letztendlich verschwindet. Die
Konsistenzbedingung besagt, dass das die Werte
hinreichend stark um ihr arithmetisches Mittel variieren. Nur auf diese Art und
Weise kommt zusätzliche Information zur Schätzung von
und
hinzu.
Das Problem an den beiden Varianzformeln ist jedoch, dass die wahre Varianz der
Störgrößen
unbekannt ist und somit geschätzt werden muss. Die positiven Quadratwurzeln der
geschätzten Varianzen werden als (geschätzte)
Standardfehler
der Regressionskoeffizienten
und
bezeichnet und sind wichtig für die Beurteilung der Anpassungsgüte
(siehe auch Standardfehler
der Regressionsparameter im einfachen Regressionsmodell).
Schätzer für die Varianz der Störgrößen
Eine erwartungstreue Schätzung der Varianz der Störgrößen ist gegeben durch
,
d.h., es gilt
(für einen Beweis, siehe
Erwartungstreuer
Schätzer für die Varianz der Störgrößen). Die positive Quadratwurzel dieser
erwartungstreuen Schätzfunktion wird auch als Standardfehler
der Regression bezeichnet.
Der Schätzwert von
wird auch mittleres
Residuenquadrat
genannt. Das mittlere Residuenquadrat wird benötigt, um Konfidenzintervalle für
und
zu bestimmen.
Das Ersetzen von
durch
in den obigen Formeln für die Varianzen der Regressionsparameter liefert die
Schätzungen
und
für die Varianzen.
Bester lineare erwartungstreue Schätzer
Es lässt sich zeigen, dass der Kleinste-Quadrate-Schätzer die beste lineare
erwartungstreue Schätzfunktion darstellt. Eine erwartungstreue Schätzfunktion
ist „besser“ als eine andere, wenn sie eine kleinere Varianz aufweist, da die
Varianz ein Maß für die Unsicherheit ist. Somit ist die beste Schätzfunktion
dadurch gekennzeichnet, dass sie eine minimale
Varianz und somit die geringste Unsicherheit aufweist. Diejenige
Schätzfunktion, die unter den linearen erwartungstreuen Schätzfunktionen die
kleinste Varianz aufweist, wird auch als bester linearer erwartungstreuer
Schätzer, kurz BLES (englisch
Best Linear Unbiased Estimator, kurz: BLUE) bezeichnet. Für alle
anderen linearen erwartungstreuen Schätzer
und
gilt somit
und
.
Auch ohne Normalverteilungsannahme ist der Kleinste-Quadrate-Schätzer ein bester linearer erwartungstreuer Schätzer.
Klassisches lineares Modell der Normalregression
Wenn man zusätzlich zu den klassischen Annahmen annimmt, dass die Störgrößen
normalverteilt
sind (),
dann ist es möglich statistische Inferenz (Schätzen und Testen) durchzuführen.
Ein Modell das zusätzlich die Normalverteilungsannahme erfüllt, wird Klassisches
lineares Modell der Normalregression genannt. Bei solch einem Modell können
dann Konfidenzintervalle
und Tests für die Regressionsparameter konstruiert werden. Insbesondere wird bei
t-Tests diese Normalverteilungsannahme benötigt, da eine t-Verteilung
als Prüfgrößenverteilung herangezogen wird, die man erhält wenn man eine
standardnormalverteilte Zufallsvariable durch die Quadratwurzel einer (um die
Anzahl ihrer Freiheitsgrade korrigierten) Chi-Quadrat-verteilten
Zufallsvariablen dividiert.
t-Tests
Die Normalverteilungsannahme
impliziert
und
und damit ergibt sich für Achsenabschnitt und Steigung die folgende t-Statistik:
.
Zum Beispiel kann ein Signifikanztest durchgeführt werden, bei dem Nullhypothese und Alternativhypothese
wie folgt spezifiziert
sind:
gegen
.
Für die Prüfgröße gilt dann:
,
wobei
das
der t-Verteilung mit
Freiheitsgraden ist.
Konfidenzintervalle
Um Konfidenzintervalle
für den Fall der linearen Einfachregression herzuleiten benötigt man die
Normalverteilungsannahme für die Störgrößen. Als -Konfidenzintervalle
für die unbekannten Parameter
und
erhält man:
und
,
wobei
das
-Quantil
der studentschen
t-Verteilung mit
Freiheitsgraden
ist und die geschätzten Standardfehler
und
der unbekannten Parameter
und
gegeben sind durch die Quadratwurzeln der geschätzten Varianzen
der Kleinste-Quadrate-Schätzer:
und
,
wobei
das mittlere
Residuenquadrat darstellt.
Vorhersage
Oft ist man daran interessiert für einen neuen Wert
die (Realisierung) der abhängigen Variablen
zu schätzen. Beispielsweise könnte
der geplante Preis eines Produktes sein und
der Absatz sein. In diesem Fall nimmt man das gleiche einfache Regressionsmodell
wie oben dargestellt an. Für eine neue Beobachtung
mit dem Wert der unabhängigen Variablen
ist die Vorhersage basierend auf der einfachen linearen Regression gegeben durch
Da man den Wert der abhängigen Variablen nie genau vorhersehen kann, ergibt sich immer ein Schätzfehler. Dieser Fehler wird als Vorhersagefehler bezeichnet und ergibt sich aus
Im Fall der einfachen linearen Regression ergibt sich für den Erwartungswert und die Varianz des Vorhersagefehlers:
und
.
Bei Punktvorhersagen dient die Angabe eines Vorhersageintervalls dazu, die
Vorhersagepräzision und -sicherheit auszudrücken. Mit Wahrscheinlichkeit
wird die Variable an der Stelle
einen Wert annehmen, der in folgendem
-Vorhersageintervall
liegt
.
Aus dieser Form des Konfidenzintervalls erkennt man sofort, dass das
Konfidenzintervall breiter wird, wenn sich die unabhängige Vorhersagevariable
vom „Gravitationszentrum“ der Daten entfernt. Schätzungen der abhängigen
Variablen sollten also im Beobachtungsraum der Daten liegen, sonst werden sie
sehr unzuverlässig.
Kausalität und Regressionsrichtung
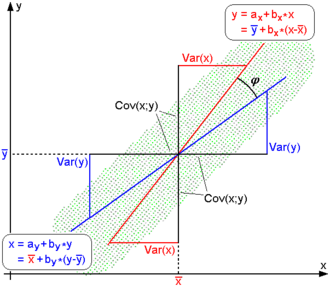
Wie in der statistischen Literatur immer wieder betont wird, ist ein hoher
Wert des Korrelationskoeffizienten
zweier Variablen
und
allein noch kein hinreichender Beleg für den kausalen
(d.h. ursächlichen) Zusammenhang von
und
,
ebenso wenig für dessen mögliche Richtung. Es ist hier nämlich ein Fehlschluss
der Art cum
hoc ergo propter hoc möglich.
Anders als gemeinhin beschrieben, sollte man es daher bei der linearen
Regression zweier Variablen
und
stets mit nicht nur einer, sondern zwei voneinander unabhängigen
Regressionsgeraden zu tun haben: der ersten für die vermutete lineare
Abhängigkeit
(Regression von
auf
),
der zweiten für die nicht minder mögliche Abhängigkeit
(Regression von
auf
).
Bezeichnet man die Richtung der -Achse
als Horizontale und die der
-Achse
als Vertikale, läuft die Berechnung des Regressionsparameter also im ersten Fall
auf das üblicherweise bestimmte Minimum der vertikalen quadratischen
Abweichungen hinaus, im zweiten Fall dagegen auf das Minimum der
horizontalen quadratischen Abweichungen.
Rein äußerlich betrachtet bilden die beiden Regressionsgeraden
und
eine Schere, deren Schnitt- und Angelpunkt der Schwerpunkt der Daten
ist. Je weiter sich diese Schere öffnet, desto geringer ist die Korrelation beider
Variablen, bis hin zur Orthogonalität
beider Regressionsgeraden, zahlenmäßig ausgedrückt durch den
Korrelationskoeffizienten
bzw. Schnittwinkel
.
Umgekehrt nimmt die Korrelation beider Variablen umso mehr zu, je mehr sich
die Schere schließt – bei Kollinearität
der Richtungsvektoren
beider Regressionsgeraden schließlich, also dann, wenn beide bildlich
übereinander liegen, nimmt
je nach Vorzeichen
der Kovarianz den Maximalwert
oder
an, was bedeutet, dass zwischen
und
ein streng linearer Zusammenhang besteht und sich (wohlgemerkt nur in diesem
einen einzigen Fall) die Berechnung einer zweiten Regressionsgeraden erübrigt.
Wie der nachfolgenden Tabelle zu entnehmen, haben die Gleichungen der beiden
Regressionsgeraden große formale Ähnlichkeit, etwa, was ihre Anstiege
bzw.
angeht, die gleich den jeweiligen Regressionsparameter sind und sich nur durch
ihre Nenner unterscheiden: im ersten Fall die Varianz von
,
im zweiten die von
:
| Regression von |
Zusammenhangsmaße | Regression von |
|---|---|---|
| Regressionskoeffizient |
Produkt-Moment-Korrelation | Regressionskoeffizient |
| Empirischer Regressionskoeffizient |
Empirischer Korrelationskoeffizient | Empirischer Regressionskoeffizient |
| Regressionsgerade |
Bestimmtheitsmaß | Regressionsgerade |
Zu erkennen ist außerdem die mathematische Mittelstellung des
Korrelationskoeffizienten und seines Quadrats, des Bestimmtheitsmaßes, gegenüber
den beiden Regressionsparameter, dadurch entstehend, dass man anstelle der
Varianzen von
bzw.
deren geometrisches
Mittel
in den Nenner setzt. Betrachtet man die Differenzen
als Komponenten eines
-dimensionalen
Vektors
und die Differenzen
als Komponenten eines
-dimensionalen
Vektors
,
lässt sich der empirische
Korrelationskoeffizient schließlich auch als Kosinus des von beiden Vektoren
eingeschlossenen Winkels
interpretieren:
Beispiel
Für das vorangegangene Beispiel aus der Sektkellerei ergibt sich folgende
Tabelle für die Regression von
auf
bzw. für die Regression von
auf
:
| Flaschenpreis |
verkaufte Menge |
||||||||
| 1 | 20 | 0 | 5 | −5 | −25 | 25 | 25 | 0,09 | 19,58 |
| 2 | 16 | 3 | 1 | −2 | −2 | 1 | 4 | 4,02 | 16,83 |
| 3 | 15 | 7 | 0 | 2 | 0 | 0 | 4 | 5,00 | 13,17 |
| 4 | 16 | 4 | 1 | −1 | −1 | 1 | 1 | 4,02 | 15,92 |
| 5 | 13 | 6 | −2 | 1 | −2 | 4 | 1 | 6,96 | 14,08 |
| 6 | 10 | 10 | −5 | 5 | −25 | 25 | 25 | 9,91 | 10,42 |
| Summe | 90 | 30 | 0 | 0 | −55 | 56 | 60 | 30,00 | 90,00 |
Daraus ergeben sich folgende Werte für die Regression von
auf
:
| Regression von | ||
|---|---|---|
| Koeffizient | Allgemeine Formel | Wert im Beispiel |
| Steigungsparameter der Regressionsgerade | ||
| Achsenabschnitt der Regressionsgerade | ||
| Geschätzte Regressionsgerade | ||
Und die Werte für die Regression von
auf
lauten:
| Regression von | ||
|---|---|---|
| Koeffizient | Allgemeine Formel | Wert im Beispiel |
| Steigungsparameter der Regressionsgerade | ||
| Achsenabschnitt der Regressionsgerade | ||
| Geschätzte Regressionsgerade | ||
Das heißt, je nachdem ob man die Regression von
auf
oder die Regression von
auf
ausführt, erhält man unterschiedliche Regressionsparameter. Für die Berechnung
des Korrelationskoeffizienten und des Bestimmheitsmaßes spielt jedoch die
Regressionsrichtung keine Rolle.
| Empirische Korrelation | ||
| Bestimmtheitsmaß |
Lineare Einfachregression durch den Ursprung
Im Fall der einfachen linearen Regression
durch den Ursprung/Regression ohne Achsenabschnitt (der Achsenabschnitt
wird nicht in die Regression miteinbezogen und daher verläuft die
Regressionsgleichung durch den Koordinatenursprung)
lautet die konkrete empirische Regressionsgerade
,
wobei die Notation
benutzt wird um von der allgemeinen Problemstellung der Schätzung eines
Steigungsparameters mit Hinzunahme eines Achsenabschnitts zu
unterscheiden. Manchmal ist es angebracht, die Regressionsgerade durch den
Ursprung zu legen, wenn
und
als proportional angenommen werden. Auch in diesem Spezialfall lässt sich die
Kleinste-Quadrate-Schätzung anwenden. Sie liefert für die Steigung
.
Dieser Schätzer für den Steigungsparameter
entspricht dem Schätzer für den Steigungsparameter
,
dann und nur dann wenn
.
Wenn für den wahren Achsenabschnitt
gilt, ist
ein verzerrter
Schätzer für den wahren Steigungsparameter
.
Für die lineare Einfachregression durch den Ursprung muss ein anderes
Bestimmtheitsmaß definiert werden, da das gewöhnliche Bestimmtheitsmaß bei einer
Regression durch den Ursprung negativ werden kann (siehe Bestimmtheitsmaß#Einfache
lineare Regression durch den Ursprung).
Die Varianz von
ist gegeben durch
.
Diese Varianz wird minimal wenn die Summe im Nenner maximal wird.
Matrixschreibweis
Der Modellcharakter des einfachen linearen Regressionsmodells wird besonders in der Matrixschreibweise mit der Datenmatrix deutlich:
mit
Diese Darstellung erleichtert die Verallgemeinerung auf mehrere Einflussgrößen (multiple lineare Regression).
Verhältnis zur multiplen linearen Regression
Die lineare Einfachregression ist ein Spezialfall der multiplen linearen Regression. Das multiple lineare Regressionsmodell
,
stellt eine Verallgemeinerung der linearen Einfachregression bzgl. der Anzahl
der Regressoren dar. Hierbei ist
die Anzahl der Regressionsparameter. Für
,
ergibt sich die lineare Einfachregression.
Lineare Einfachregression in R
Als einfaches Beispiel wird der Korrelationskoeffizient zweier Datenreihen berechnet:
# Groesse wird als numerischer Vektor
# durch den Zuweisungsoperator "<-" definiert:
Groesse <- c(176, 166, 172, 184, 179, 170, 176)
# Gewicht wird als numerischer Vektor definiert:
Gewicht <- c(65, 55, 67, 82, 75, 65, 75)
# Berechnung des Korrelationskoeffizienten nach Pearson mit der Funktion "cor":
cor(Gewicht, Groesse, method = "pearson")
Das Ergebnis lautet 0.9295038.
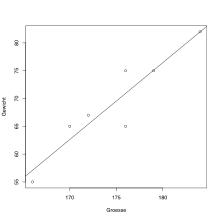
Mithilfe der Statistiksoftware R kann eine lineare Einfachregression durchgeführt werden. Dies kann in R durch die Funktion lm ausgeführt werden, wobei die abhängige Variable von den unabhängigen Variablen durch die Tilde getrennt wird. Die Funktion summary gibt die Koeffizienten der Regression und weitere Statistiken hierzu aus:
# Lineare Regression mit Gewicht als Zielvariable
# Ergebnis wird als reg gespeichert:
reg <- lm(Gewicht~Groesse)
# Ausgabe der Ergebnisse der obigen linearen Regression:
summary(reg)
Diagramme lassen sich einfach erzeugen:
# Streudiagramm der Daten:
plot(Gewicht~Groesse)
# Regressionsgerade hinzufügen:
abline(reg)
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.07. 2025