Quantil (Wahrscheinlichkeitstheorie)
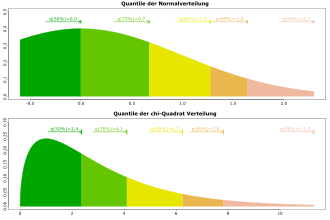
Ein Quantil ist ein Lagemaß in der Statistik. Anschaulich ist ein Quantil ein Schwellenwert: ein bestimmter Anteil der Werte ist kleiner als das Quantil, der Rest ist größer. Das 25-%-Quantil beispielsweise ist der Wert, für den gilt, dass 25 % aller Werte kleiner sind als dieser Wert. Quantile formalisieren praktische Aussagen wie „25 % aller Frauen sind kleiner als 1,62 m“ – wobei 1,62 m hier das 25-%-Quantil ist.
Genauer ist das -Quantil,
wobei
eine reelle Zahl zwischen 0 und 1 ist, ein Wert einer Variablen oder Zufallsvariablen, der
die Menge aller Merkmalswerte (salopp „die Verteilung“) in zwei Abschnitte
unterteilt: Links vom
-Quantil
liegt der Anteil
aller Beobachtungswerte oder der Gesamtzahl der Zufallswerte oder der Fläche
unter der Verteilungskurve; rechts davon liegt der jeweilige restliche Anteil
.
Die Zahl
heißt auch der Unterschreitungsanteil.
Spezielle Quantile sind der Median, die Quartile, die Quintile, die Dezile und die Perzentile.
Als Quantil der Ordnung
oder
-Quantil
(veraltet auch „Fraktil“) wird in der Statistik
ein Merkmalswert bezeichnet, unterhalb dessen ein vorgegebener Anteil
aller Fälle der Verteilung liegt. Jeder Wert unterhalb von
unterschreitet diesen vorgegebenen Anteil. Dabei kann der
Unterschreitungsanteil
auch als eine reelle Zahl zwischen 0 (gar kein Fall der Verteilung) und 1 (alle
Fälle bzw. 100 % der Verteilung) angegeben werden.
Definition
Für Wahrscheinlichkeitsverteilungen
Gegeben sei eine Wahrscheinlichkeitsverteilung
auf
,
also den reellen Zahlen, versehen
mit der Borelschen
σ-Algebra.
Dann heißt eine reelle Zahl
ein p-Quantil (von
),
wenn gilt:
und
.
Insbesondere kann mehr als ein p-Quantil existieren.
Für Zufallsvariablen
Gegeben sei eine reelle Zufallsvariable
.
Dann heißt eine reelle Zahl
ein p-Quantil (von
),
wenn gilt:
und
.
Damit ist das p-Quantil der Zufallsvariable
genau das p-Quantil ihrer
Verteilung
.
Definition über Verteilungsfunktionen
Ebenso lassen sich Quantile auch über Verteilungsfunktionen
definieren. Ist
die Verteilungsfunktion von
oder von
,
so heißt
ein p-Quantil, wenn
und
.
Hierbei bezeichnet
den linksseitigen
Grenzwert.
Bestimmung und Beispiele
Bei stetigen Verteilungsfunktionen
Ist die Verteilungsfunktion
der Zufallsvariable oder der Wahrscheinlichkeitsverteilung stetig, die Verteilung also
eine stetige
Wahrscheinlichkeitsverteilung, so vereinfacht sich die Definition. Das
p-Quantil
ist dann eine Lösung der Gleichung
Dies folgt aus der Definition des p-Quantils über die Verteilungsfunktion, da
die linksseitige Stetigkeit im zweiten Kriterium aufgrund der Stetigkeit dann
mit dem Funktionswert an der Stelle
übereinstimmt.
- Beispiel
Betrachtet man die Exponential-Verteilung
mit Parametern ,
so besitzt sie die Verteilungsfunktion
Auflösen der Gleichung
für ein
nach
liefert das p-Quantil. Hier ist
.
Ist die Verteilungsfunktion auf einem Intervall konstant, so existieren mehrdeutige p-Quantile. Betrachtet man die Verteilungsfunktion
,
so besitzt die Gleichung
unendlich viele Lösungen. Jedes
aus dem Intervall
ist dann ein
-Quantil
(also ein Median).
Bei Existenz einer Wahrscheinlichkeitsdichtefunktion
Besitzt die Zufallsvariable beziehungsweise die Wahrscheinlichkeitsverteilung
eine Wahrscheinlichkeitsdichtefunktion
,
(sie ist demnach eine Absolutstetige
Verteilung), so ist das p-Quantil
Lösung der Gleichung
.
Dies folgt direkt aus der Tatsache, dass absolutstetige Verteilungen immer eine stetige Verteilungsfunktion besitzen, diese sich über das Integral bestimmen lässt und der Aussage im obigen Abschnitt.
- Beispiel
Bei Verteilungen mit Wahrscheinlichkeitsdichtefunktionen treten mehrdeutige Quantile dann auf, wenn die Dichtefunktion auf einem Intervall konstant null ist. So besitzt die oben über die Verteilungsfunktion definierte Verteilung die Wahrscheinlichkeitsdichtefunktion
Der oben hergeleitete mehrdeutige Median wird hier durch das Intervall
verursacht, auf dem die Wahrscheinlichkeitsdichtefunktion konstant gleich null
ist.
Nicht-Eindeutigkeit und eindeutige Definition


Ist
invertierbar, beispielsweise bei stetigen Verteilungen mit streng monotoner
Verteilungsfunktion, fallen obere und untere Grenze zusammen, wodurch die
obengenannte Menge einelementig bzw. das p-Quantil eindeutig wird.
Die Funktion
heißt Quantilsfunktion
oder verallgemeinerte inverse Verteilungsfunktion, der Wert
,
zuweilen auch
geschrieben, dementsprechend
-Quantil
von
oder von
(ist klar, welche Zufallsvariable gemeint ist, wird diese oft auch
weggelassen.).
In den Grafiken rechts ist
das eindeutige
-Quantil,
ferner ist
das eindeutige
-Quantil,
-Quantil
sowie
-Quantil.
Hat
eine Sprungstelle bei
,
ist also
,
so gilt
für fast alle
mit
.
In der Grafik rechts oben ist
und daher .
Ist
für ein
nicht invertierbar, also ein Stück weit konstant, besitzt die Quantilfunktion
für dieses
eine Sprungstelle, bei der sie als Funktionswert das kleinstmögliche
p-Quantil angibt. In der Grafik ist
das kleinstmögliche
-Quantil,
das größtmögliche
-Quantil, und
- jedes
ein weiteres
-Quantil.
Beim oft verwendeten 50%-Quantil sind zur besseren Unterscheidung sogar
eigene Begrifflichkeiten üblich: Der Untermedian
ist das kleinstmögliche 50%-Quantil, der Median
das mittlere 50%-Quantil und der Obermedian
das größtmögliche 50%-Quantil, wobei alle drei deutlich auseinanderfallen
können.
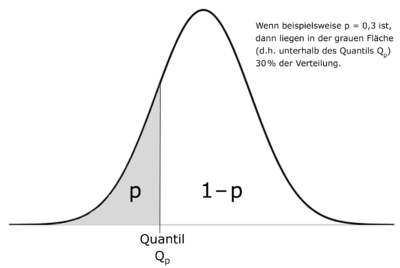
Beispiel
Das Quantil
(also das 0,3-Quantil) ist der Wert des Punktes einer Verteilung, unterhalb
dessen sich 30 % aller Fälle der Verteilung befinden.
Besondere Quantile
Für einige bestimmte
haben die
-Quantile
zusätzliche Bezeichnungen.
Median
Der Median oder Zentralwert entspricht dem Quantil
(0,5-Quantil). Es erfolgt also eine Einteilung aller Fälle der Verteilung in
zwei umfangsgleiche Teile. Bei jeder Einteilung in eine ungerade Anzahl von
-Quantilen
mit äquidistant-verteilten
(was eine gerade Anzahl umfangsgleicher Teile impliziert) entspricht der Median
jeweils dem mittleren Quantil (beispielsweise dem 2. Quartil Q2 oder dem 50.
Perzentil P50).
Terzil
Durch Terzile wird die größengeordnete Menge der Werte in drei Abschnitte gleichen Umfangs geteilt: unteres, mittleres und oberes Drittel.
Quartil

Quartile (lateinisch „Viertelwerte“) sind
die Quantile
(0,25-Quantil),
(0,5-Quantil = Median) und
(0,75-Quantil), die auch als Q1 („unteres Quartil“), Q2 („mittleres
Quartil“) und Q3 („oberes Quartil“) bezeichnet werden. Sie sind die
in der Statistik mit am häufigsten
verwendete Form der Quantile.
Der (Inter-)Quartilabstand oder auch (Inter-)Quartilsabstand
(englisch interquartile range) bezeichnet die Differenz zwischen dem
oberen und dem unteren Quartil, also
und umfasst daher 50 % der Verteilung. Der Quartilabstand wird als Streuungsmaß
verwendet.
Siehe auch: Streuung (Statistik)
Quintil
Durch Quintile (lateinisch „Fünftelwerte“) wird die Menge der Werte der
Verteilung in 5 umfangsgleiche Teile zerlegt. Unterhalb des ersten Quintils,
d.h. des Quantils ,
liegen 20 % der Werte der Verteilung, unterhalb des zweiten Quintils
(Quantil
)
40 % usw.
Dezil
Durch Dezile (lateinisch „Zehntelwerte“) wird die Menge der verteilten Werte
in 10 umfangsgleiche Teile zerlegt. Entsprechend liegen dann z.B.
unterhalb des dritten Dezils (Quantil )
30 % der Werte. Dezile teilen ein der Größe nach geordnetes Datenbündel in
10 umfangsgleiche Teile. Das 10-%-Dezil (oder 1. Dezil) gibt an, welcher Wert
die unteren 10 % von den oberen 90 % der Datenwerte trennt, das 2.
Dezil, welcher Wert die unteren 20 % von den oberen 80 % der Werte
trennt, usw. Der Abstand zwischen dem 10-%-Dezil und dem 90-%-Dezil heißt
Interdezilbereich.
Perzentil
Durch Perzentile (lateinisch „Hundertstelwerte“), auch Prozentränge
genannt, wird die Verteilung in 100 umfangsgleiche Teile zerlegt. Perzentile
teilen die Verteilung also in 1-%-Segmente auf. Daher können Perzentile als
Quantile betrachtet werden, bei denen
eine ganze Zahl ist. So entspricht das Quantil
dem Perzentil P97: unterhalb dieses Punktes liegen 97 % aller Fälle der
Verteilung.
a-Fraktil
Für
aus
wird das
-Quantil
auch als
-Fraktil
bezeichnet. Diese Unterteilung wird z.B. in der als „Paretoprinzip“
bezeichneten Vermutung verwendet.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.06. 2021