Ausgleichungsrechnung

Anpassung einer rauschenden Kurve durch ein asymmetrisches Peak-Modell mithilfe des iterativen Gauß-Newton-Verfahren. Oben: Roh-Daten und Modell; Unten: Entwicklung der normalisierten quadrierten Summe der Fehlerterme

Die Ausgleichungsrechnung (auch Ausgleichsrechnung, Ausgleichung, Parameterschätzung oder Anpassung genannt) ist eine mathematische Optimierungsmethode, mit deren Hilfe für eine Reihe von Messdaten die unbekannten Parameter ihres geometrisch-physikalischen Modells oder die Parameter einer vorgegebenen Funktion bestimmt oder geschätzt werden sollen. In der Regel werden mit ihr überbestimmte Probleme gelöst. Regression und Fit(ting) sind häufig verwendete Verfahren der Ausgleichsrechnung.

Ziel der Ausgleichung ist, dass sich das endgültige Modell bzw. die Funktion den Daten und ihren unvermeidlichen kleinen Widersprüchen bestmöglich anpasst. Im Allgemeinen wird die Berechnung mit der Methode der kleinsten Quadrate durchgeführt. Diese Methodik bedeutet, dass an den Parametern kleine Verbesserungen angebracht werden, so dass die Summe der Quadrate aller einzelnen Abweichungen zwischen Mess- und Modelldaten minimal werden soll. Bei zufällig verteilten Modell- oder Messfehlern führt dies zum wahrscheinlichsten Wert für die zu berechnenden Unbekannten. Die verbleibenden kleinen Reste werden Residuen genannt und lassen Aussagen über die Genauigkeit und Zuverlässigkeit des Mess- und Datenmodells zu.

Ausgleichung und Approximationstheorie

Da kleine Widersprüche in allen redundanten, auf Zuverlässigkeit geprüften Daten auftreten, ist der Umgang mit diesen meist statistisch verteilten Restabweichungen zur wichtigen Aufgabe in verschiedenen Wissenschaften und der Technik geworden. Neben der glättenden Wirkung auf streuende Daten wird die Ausgleichungsrechnung auch zur Milderung von Diskrepanzen etwa in den Sozialwissenschaften verwendet.

Diese Suche nach den naturnahen, wahrscheinlichsten Werten von Systemen oder Messreihen ist in der Sprache der Approximationstheorie die Schätzung von unbekannten Parametern eines mathematischen Modells. Die dabei meist verwendete Methode der kleinsten Quadrate (englisch least mean squares oder kurz least squares) entspricht dem Gauß-Markow-Modell. Im einfachsten Fall hat eine Ausgleichung zum Ziel, eine größere Anzahl empirischer Mess- oder Erhebungsdaten durch eine Kurve zu beschreiben und die Restabweichungen (Residualkategorie) zu minimieren. Eine solche Kurvenanpassung kann auch erstaunlich genau freiäugig-grafisch durch Betrachten der Datenreihe durchgeführt werden, was die naturnahe Charakteristik der Quadratabweichungsminimierung unterstreicht.

Die Ausgleichungsrechnung wurde um 1800 von Carl Friedrich Gauß für ein Vermessungsnetz der Geodäsie und für die Bahnbestimmung von Planetoiden entwickelt. Seither werden Ausgleichungen in allen Natur- und Ingenieurwissenschaften durchgeführt, bisweilen auch in den Wirtschafts- und Sozialwissenschaften. Die Ausgleichung nach dem Gauß-Markow-Modell liefert das bestmögliche Ergebnis, wenn die Residuen zufällig sind und einer Normalverteilung folgen. Unterschiedlich genaue Messwerte werden durch Gewichtung abgeglichen.

Enthalten die Messungen oder Daten allerdings auch systematische Einflüsse oder grobe Fehler, dann ist das ausgeglichene Ergebnis verfälscht und die Residuen weisen einen Trend hinsichtlich der Störeinflüsse auf. In solchen Fällen sind weitere Analysen erforderlich wie etwa eine Varianzanalyse oder die Wahl eines robusten Schätzverfahrens.

Einführung

Im einfachsten Fall handelt es sich um die Ausgleichung der Messabweichungen (Verbesserung, Residuum) nach der Methode der kleinsten Quadrate. Hierbei werden die Unbekannten (die Parameter) des Modells so bestimmt, dass die Quadratsumme der Messabweichungen aller Beobachtungen minimal wird. Die geschätzten Parameter stimmen dann erwartungstreu mit dem theoretischen Modell überein. Alternativ kann die Ausgleichung auch nach einer anderen Residuenbewertungsfunktion erfolgen, z.B. durch Minimierung der Summe oder des Maximums der Beträge der Messabweichungen.

Damit handelt es sich um ein Optimierungsproblem. Die Rechenschritte einer Ausgleichung vereinfachen sich wesentlich, wenn die Beobachtungen als normalverteilt und unkorreliert angesehen werden können. Falls ungleiche Genauigkeiten der Messgrößen vorliegen, kann dies durch Gewichtung berücksichtigt werden. Weitergehende stochastische Eigenschaften der Beobachtungen können in der Regressionsanalyse ergründet werden.

Funktionales und stochastisches Modell

Jeder Ausgleichung geht eine Modellbildung voraus. Hierbei wird im Allgemeinen zwischen funktionalem Modell und stochastischem Modell unterschieden.

Ein funktionales Modell beschreibt hierbei die mathematischen Relationen zwischen den bekannten (konstanten), unbekannten und den beobachteten Parametern. Die Beobachtungen stellen dabei stochastische Größen (Zufallsvariable) dar, z.B. mit zufälligen Störungen überlagerte Messungen.
- Als einfaches Beispiel sei ein Dreieck genannt, in dem überzählige Messungen zu geometrischen Widersprüchen führen (z.B. Winkelsumme ungleich 180°). Das funktionale Modell dazu sind die Formeln der Trigonometrie; die Störungen können z.B. kleine Zielabweichungen bei jeder Winkelmessung sein.
Das stochastische Modell beschreibt die Varianzen und Kovarianzen der beobachteten Parameter.

Das Ziel der Ausgleichung ist eine optimale Ableitung der unbekannten Werte (Parameter, z.B. die Koordinaten der Messpunkte) und der Maße für ihre Genauigkeit und Zuverlässigkeit im Sinne einer Zielfunktion. Für letztere wählt man meistens die minimale Summe der Abweichungsquadrate, doch können es für Sonderfälle beispielsweise auch minimale Absolutwerte oder andere Zielfunktionen sein.

Lösungsverfahren

Je nach funktionalem und stochastischem Modell werden verschiedene Ausgleichungsmodelle benutzt.

Das Hauptunterscheidungsmerkmal dabei ist,

ob sich alle Beobachtungen als Funktionen von Unbekannten und Konstanten darstellen lassen,
ob die Beobachtungen voneinander stochastisch unabhängig oder korreliert sind,
ob die Relationen nur Beobachtungen und Konstanten aufweisen, jedoch keinerlei Unbekannte enthalten,
ob es unter der Menge der Relationen auch solche gibt, die ausschließlich Beziehungen unter Konstanten und Unbekannten beschreiben und damit Restriktionen zwischen Unbekannten beschreiben.
Bei gemischtem Auftreten von sehr verschiedenen Messgrößen – etwa bei geometrischen und physikalischen Messungen – wurden die Methoden der Ausgleichsrechnung von einigen Mathematikern und Geodäten um 1970 zur sogenannten Kollokation erweitert. Sie wird unter anderem für die Geoidbestimmung verwendet.

Die Ausgleichungsmodelle heißen:

Ausgleichung nach vermittelnden Beobachtungen: Die einzelnen Beobachtungen sind Funktionen der unbekannten Parameter.
Ausgleichung nach vermittelnden Beobachtungen mit Bedingungen zwischen den Unbekannten: Es bestehen zusätzliche Bedingungen zwischen den unbekannten Parametern.
Ausgleichung nach bedingten Beobachtungen (bedingte Ausgleichung): Es werden Bedingungsgleichungen für die Beobachtungen aufgestellt, in denen die unbekannten Parameter nicht vorkommen. Die unbekannten Parameter können dann aus den ausgeglichenen Beobachtungen berechnet werden.
Allgemeinfall der Ausgleichung: Es werden funktionale Beziehungen zwischen Beobachtungen und Parametern aufgestellt, in denen die Beobachtungen nicht explizit als Funktion der Parameter vorkommen.

Grafisches Verfahren

Die gleichen Messpunkte mit zwei verschiedenen Ausgleichslinien

Während dem mathematischen Lösungsverfahren ein Modell zugrunde gelegt werden muss, ist das grafische Verfahren ohne solche Annahme möglich. Hier wird eine stetig gekrümmte ausgleichende Linie den Messpunkten angenähert. Je nach Hintergrundwissen (Erwartung an den Verlauf) oder persönlicher Bewertung (einzelne Messpunkte als „Ausreißer“) kann die Linie allerdings durchaus unterschiedlich ausfallen. Zum Zeichnen solcher Linien gibt es Schablonen(sätze), speziell die sog. Burmester-Schablonen sind gängig.

Definition

Allgemeine Ausgleichsrechnung

Gegeben seien die Messpunkte $(t_{i},b_{i})\in \mathbb {R} ^{2},\;i=1,\dotsc ,m$ . Die Modellfunktion $\phi$ habe Parameter $x_{i}\in \mathbb {R} ,\;i=1,\dotsc ,n$ , wobei $m\geq n$ gelten soll. Die Modellfunktion $\phi$ hängt dabei von den Messpunkten $t_{i}$ und den Parametern $x_{i}$ ab und soll die Messpunkte $b_{i}$ annähern. Kurz geschrieben als:

$\phi (t_{i};x_{1},\dotsc ,x_{n})\sim b_{i},\quad i=1,\dotsc ,m.$

Es werden nun Parameter $x\in \mathbb {R} ^{n}$ gesucht, welche die Messpunkte „gut“ annähern:

$\|b-\phi (x)\|=\min _{y\in \mathbb {R} ^{n}}\|b-\phi (y)\|$ ,

wobei die folgenden Definitionen getroffen wurden:

${\begin{aligned}b&:=(b_{i})_{i=1,\dotsc ,m}\\\phi (x)&:=\phi (t_{i};x_{1},\dotsc ,x_{n}).\end{aligned}}$

Wie „gut“ die Modellfunktion mit den gewählten Parametern die Messpunkte annähert, hängt von der gewählten Norm $\|\cdot \|$ ab. Die folgenden sind gebräuchlich:

${\begin{aligned}\|\cdot \|_{2}\quad &{\text{nach Gauß – kleinste Fehlerquadrate}}\\\|\cdot \|_{1}\quad &L^{1}{\text{-Ausgleichsrechnung}}\\\|\cdot \|_{\infty }\quad &{\text{Tschebyscheff-Ausgleichsrechnung}}.\end{aligned}}$

Lineare Ausgleichsrechnung

Die Abhängigkeit der Modellfunktion von den Parametern kann im Spezialfall als linear angenommen werden:

$\phi (x)=Ax\quad {\text{mit}}\;A\in \mathbb {R} ^{m\times n}.$

Das lineare Ausgleichsproblem lautet nun: Für $b\in \mathbb {R} ^{m},A\in \mathbb {R} ^{m\times n}$ suche $x\in\R^n$ , sodass

$\|b-Ax\|_{2}=\min _{y\in \mathbb {R} ^{n}}\|b-Ay\|_{2}$

gilt.

Diese Definition ist äquivalent dazu, dass $x\in\R^n$ die Normalengleichung erfüllt:

$A^{T}Ax=A^{T}b.$

Die Existenz einer Lösung $x\in\R^n$ ist stets gegeben und die Eindeutigkeit, falls vollen Rang hat: ${\mathrm {rang}}(A)=n$ .

Konditionierung der linearen Ausgleichsrechnung

Die Kondition des linearen Ausgleichsproblem hängt von der Konditionszahl der Matrix ab, wie aber auch von einer geometrischen Eigenschaft des Problems.

Sei im Folgenden $A\in \mathbb {R} ^{m\times n},m\geq n$ mit vollem Rang und $x^{*}\in \mathbb {R} ^{n}$ die Lösung des Ausgleichsproblems. Aufgrund der Orthogonalität der Anpassung:

$b-Ax^{*}\perp Ax^{*}$

gibt es ein eindeutiges $\Theta \in [0,{\frac {\pi }{2}}]$ mit (nach Pythagoras):

$\cos \Theta ={\frac {\|Ax^{*}\|}{\|b\|}}\quad {\text{und}}\quad \sin \Theta ={\frac {\|b-Ax^{*}\|}{\|b\|}}.$

Dies soll die geometrische Eigenschaft des Problems sein.

Gestörte rechte Seite

Seien $x^{*}$ und ${\tilde {x}}^{*}$ die Lösungen des linearen Ausgleichsproblems mit rechter Seite bzw. gestörter rechter Seite ${\tilde {b}}$ , also:

$A^{T}Ax^{*}=A^{T}b\quad {\text{und}}\quad A^{T}A{\tilde {x}}^{*}=A^{T}{\tilde {b}}.$

Die Konditionierung dieses Problems lautet nun:

${\frac {\|x^{*}-{\tilde {x}}^{*}\|_{2}}{\|x^{*}\|_{2}}}\leq {\frac {\kappa _{2}(A)}{\cos \Theta }}{\frac {\|b-{\tilde {b}}\|_{2}}{\|b\|_{2}}}.$

Für $\Theta =0$ erhält man somit die Konditionierung des LGS Ax=b und für $\Theta ={\frac {\pi }{2}}$ beliebig große Störempfindlichkeit.

Gestörte Matrix

Seien $x^{*}$ bzw. ${\tilde {x}}^{*}$ die Lösung des linearen Ausgleichsproblems zur Matrix bzw. ${\tilde {A}}$ , also:

$A^{T}Ax^{*}=A^{T}b\quad {\text{und}}\quad {\tilde {A}}^{T}{\tilde {A}}{\tilde {x}}^{*}={\tilde {A}}^{T}b.$

Die Konditionierung dieses Problems lautet nun:

${\frac {\|x^{*}-{\tilde {x}}^{*}\|_{2}}{\|x^{*}\|_{2}}}\leq \left(\kappa _{2}(A)+\kappa _{2}(A)^{2}\tan \Theta \right){\frac {\|A-{\tilde {A}}\|_{2}}{\|A\|_{2}}}.$

Unterschiede zwischen Regression und Anpassung

Regression und Anpassung sind nicht synonym und unterscheiden sich in den Problemstellungen und den auszuwertenden Daten.

Regression

Eine Regression untersucht eine mögliche Korrelation zwischen zwei oder mehrere Merkmalen mit einem angenommenen linearen Zusammenhang (hier zweidimensional (x,y(x)) ). Dabei werden die Datenpunkte als konstant bzw. fest angenommen. Mit einer angenommenen kontinuierlichen Funktion untersucht die Regression, wie sehr sich die Datenpunkte mit der angenommenen Funktion beschreiben lassen. Die einzige stochastische Größe ist das Residuum. Die geschätzten Regressionsparameter (bei einem linearen Zusammenhang z.B. $\beta _{0},\beta _{1}$ ) der Regressionsfunktion sind feste Größen: $y_{i}=\beta _{0}+\beta _{1}x_{i}+\varepsilon$ .

Anpassung

Unter einer Anpassung wird eine Funktionsanpassung verstanden unter Berücksichtigung von Messfehlern oder Unsicherheiten der Messpunkte $\left(x,y\pm \delta _{{y}}\right)$ . Die resultierenden Funktionsparameter sind dann wie die Messwerte mit einer Unsicherheit behaftet. Die geläufigste Methode einer Anpassung ist die Benutzung der Methode der kleinsten Quadrate, wobei gaußverteilte Fehlerterme angenommen werden. Die Anpassungsgüte kann durch das Bestimmtheitsmaß beurteilt werden.

Vergleichbar ist ein einzelner Messwert mit Fehler, hier liegt der „wahre“ Wert mit einer gewissen Wahrscheinlichkeit innerhalb der Fehlerbalken; der zentrale Wert ist hierbei nur der wahrscheinlichste Wert.

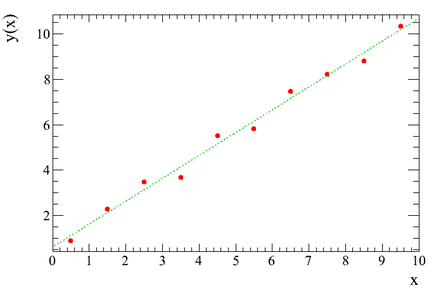Beispiel für Regression: Für die Wertepaare $\left(x,y\right)$ wird ein linearer Zusammenhang (Regressionsgerade) angenommen. Die Stützstellen $x_{i}$ sind konstant; hingegen unterliegen die Abstände $\epsilon _{i}$ der $y_{i}$ einem stochastischen Modell.
Fit mit einem linearen Zusammenhang. Der Fehler eines Datenpunktes ist hier die Wurzel aus dem Messwert. Obwohl die Zentralwerte der Messpunkte und das zentrale Fitergebnis gleich sind wie im Beispiel zuvor, ist die Kurvenschar aller wahrscheinlichen Funktionen eine andere.
Fit mit einem linearen Zusammenhang der Datenpunkte. Die Datenpunkte haben alle den gleichen Fehler. Das Ergebnis des Fits ist mit einer gewissen Wahrscheinlichkeit der „wahre“ funktionale Zusammenhang zwischen den Datenpunkten.

Zusammenfassung

Beide Methoden können in Spezialfällen die gleichen Funktionsparameter liefern, zum Beispiel bei linearen Zusammenhängen mit gleichen Unsicherheiten der Messwerte bei der Anpassung.

Bei der Anpassung ist die Methode der kleinsten Quadrate nur bedingt geeignet, wenn Datenpunkte Fehler haben, die nicht gaußförmig verteilt sind. Auch muss bei einer Transformation von Datenpunkten beachtet werden, dass die Unsicherheiten der Datenpunkte ebenso mittransformiert werden müssen (Beispiel: eine exponentielle Verteilung mit Unsicherheiten soll linearisiert werden).

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de