
Bestimmtheitsmaß
Das Bestimmtheitsmaß, auch Determinationskoeffizient (von lateinisch determinatio
„Abgrenzung, Bestimmung“ bzw. determinare „eingrenzen“, „festlegen“,
„bestimmen“ und coefficere „mitwirken“), bezeichnet mit ,
ist in der Statistik eine Kennzahl zur Beurteilung der
Anpassungsgüte
einer Regression –
beispielsweise, um zu bewerten, wie gut Messwerte
zu einem Modell passen. Das
Bestimmtheitsmaß beruht auf der Quadratsummenzerlegung, bei der die
totale
Quadratsumme in die (durch das Regressionsmodell) erklärte
Quadratsumme und in die Residuenquadratsumme
zerlegt wird.
In der einfachen und multiplen linearen Regression ist das Bestimmtheitsmaß definiert als „der Anteil der durch die Regression erklärten Quadratsumme an der zu erklärenden totalen Quadratsumme“ und gibt an, wie viel Streuung in den Daten durch ein vorliegendes lineares Regressionsmodell „erklärt“ werden kann. Das Bestimmtheitsmaß entspricht bei der einfachen linearen Regression und der multiplen linearen Regression genau dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten. Ansonsten existieren unterschiedliche Definitionen, wie zum Beispiel bei den Pseudo-Bestimmtheitsmaßen. Das Bestimmtheitsmaß steht in enger Beziehung zu weiteren Modellgütemaßen zur Prüfung der Regressionsfunktion, wie z.B zum Standardfehler der Regression und zur F-Statistik. Weil das Bestimmtheitsmaß durch die Aufnahme zusätzlicher Variablen wächst und die Gefahr der Überanpassung besteht, wird für praktische Anwendungen meist das adjustierte Bestimmtheitsmaß verwendet. Das adjustierte Bestimmtheitsmaß „bestraft“ im Gegensatz zum unadjustierten Bestimmtheitsmaß die Aufnahme jeder neu hinzugenommenen erklärenden Variable.
Obwohl das Bestimmtheitsmaß die am häufigsten benutzte Kennzahl ist, um die globale Anpassungsgüte einer Regression zu quantifizieren, wird es oft fehlinterpretiert und falsch angewendet, auch da bei einer Regression durch den Ursprung zahlreiche alternative Definitionen des Bestimmtheitsmaßes nicht äquivalent sind. Das Bestimmtheitsmaß ist ein reines Zusammenhangsmaß. So ist es nicht möglich das Bestimmtheitsmaß zu verwenden, um einen direkten kausalen Zusammenhang zwischen den Variablen nachzuweisen. Außerdem zeigt das Bestimmtheitsmaß nur die Größe des Zusammenhangs zwischen den Variablen, aber nicht, ob dieser Zusammenhang statistisch signifikant ist.
Einführung in die Problemstellung
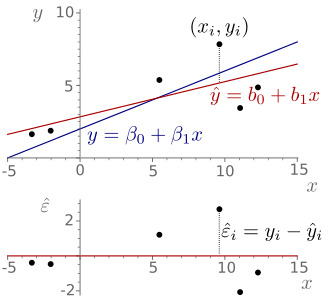
Gegeben sind
Messungen
,
d.h. bei dem
-ten
Wertepaar
wird einem Wert
(zB. Größe einer Person) ein Messwert
(z.B. das gemessene Gewicht der Person) zugeordnet. Dazu berechnet man den
empirischen
Mittelwert
(z.B. das mittlere Gewicht der Probanden).
Ferner gibt es einen Schätzer
(Modellfunktion), der jedem Wert
(z.B. Größe) einen Schätzwert
(geschätztes Gewicht für eine Person mit Größe
)
zuordnet. Die Abweichung einer Schätzung
von der zugehörigen Messung
ist durch
gegeben und wird „Residuum“
genannt. Bei der einfachen
linearen Regression, die zum Ziel hat, das Absolutglied (englisch
intercept)
,
die Steigung (englisch
slope)
und die Störgrößenvarianz
zu schätzen, wird der Schätzer anschaulich durch die Regressionsgerade
beschrieben und mathematisch durch die Stichproben-Regressionsfunktion
definiert. Die beiden Parameterschätzer
und
werden auch als Kleinste-Quadrate-Schätzer bezeichnet.[A
1] Wenn das zugrundeliegende Modell ein von Null verschiedenes Absolutglied
enthält, stimmt der empirische Mittelwert der Schätzwerte
mit dem der beobachteten Messwerte
überein, also
(für einen Beweis siehe Abschnitt Matrixschreibweise).
Es empfiehlt sich, nach der Schätzung der Regressionsparameter die Regressionsgerade gemeinsam mit den Datenpunkten in ein Streudiagramm einzuzeichnen. Auf diese Weise bekommt man eine Vorstellung davon, wie „gut“ die Punkteverteilung durch die Regressionsgerade wiedergegeben wird. Je enger die Datenpunkte um die Regressionsgerade herum konzentriert sind, d.h. je kleiner also die Residuenquadrate sind, desto „besser“. In diesem Zusammenhang ist allerdings zu beachten, dass die Residuenquadrate typischerweise klein sind, wenn die abhängige Variable eine geringe Variabilität aufweist. Die geforderte Kleinheit der Residuenquadrate muss also in Relation zur Streuung der abhängigen Variablen betrachtet werden.
Ein Maß zur Beurteilung der Anpassungsgüte sollte außerdem die Streuung
der Messwerte und die der geschätzten Werte in Relation setzen. Die Streuung der
jeweiligen Werte um ihren Mittelwert kann mithilfe der „Summe der
Abweichungsquadrate“ (Summe der Quadrate bzw. englisch
Sum of Squares, kurz: SQ oder SS)
gemessen werden. Das „mittlere
Abweichungsquadrat“ stellt die empirische
Varianz dar. Die Streuung der Schätzwerte
um ihren Mittelwert
kann durch
gemessen werden und die Streuung der Messwerte
um das Gesamtmittel
kann durch
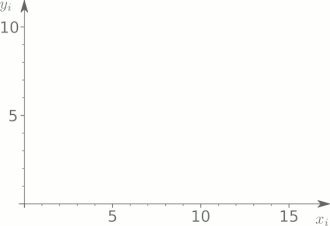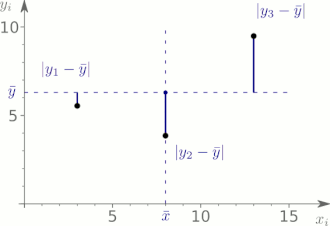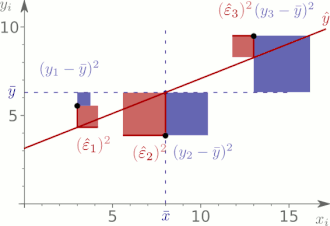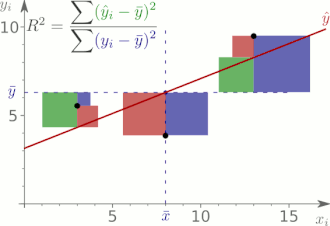
gemessen werden. Erstere stellt die durch die Regression „erklärte
Quadratsumme“ (Summe der Quadrate der Erklärten
Abweichungen bzw. englisch
Sum of Squares Explained, kurz: SQE
oder SSE) und letztere stellt die „zu erklärende Quadratsumme“ bzw. die
„totale
Quadratsumme“ (Summe der Quadrate der Totalen
Abweichungen bzw. englisch
Sum of Squares Total, kurz: SQT oder
SST) dar. Das Verhältnis
dieser beiden Größen wird das Bestimmtheitsmaß der Regression genannt (für die
Berechnung des Bestimmtheitsmaßes zum Körpergröße-Körpergewicht-Beispiel mittels
statistischer Software, siehe Bestimmtheitsmaß
in R). Das Bestimmtheitsmaß zeigt, wie gut die durch die Schätzung
gefundene Modellfunktion zu den Daten passt, d.h. wie gut sich die
konkrete empirische Regressionsgerade einer angenommenen wahren Gerade
annähert. Die durch die Regression „nicht erklärten Abweichungen“
(Restabweichungen), d.h. die Abweichungen der Datenpunkte von der
Regressionsgeraden werden durch die Regression „nicht erklärte Quadratsumme“
bzw. die Residuenquadratsumme
(Summe der Quadrate der Restabweichungen (oder:
„Residuen“) bzw. englisch
Sum of Squares Residual, kurz: SQR
oder SSR) erfasst, die durch
gegeben ist.[A 2]
Das Bestimmtheitsmaß
Definition
Das Bestimmtheitsmaß der Regression, auch empirisches Bestimmtheitsmaß,[A 3] ist eine dimensionslose Maßzahl die den Anteil der Variabilität in den Messwerten der abhängigen Variablen ausdrückt, der durch lineare Modell „erklärt“ wird. Gegeben die Quadratsummenzerlegung ist das Bestimmtheitsmaß der Regression definiert als das Verhältnis der durch die Regression erklärten Quadratsumme zur totalen Quadratsumme:[A 4]
,
wobei angenommen wird, dass für die totale Quadratsumme
gilt. Dies ist praktisch immer erfüllt, außer für den Fall, dass die Messwerte
der abhängigen Variable keinerlei Variabilität aufweisen, d.h.
.
In diesem Falle ist das Bestimmtheitsmaß nicht definiert.
Die zweite Gleichheit, die sich mithilfe der Quadratsummenzerlegung zeigen
lässt, ist eine alternative Berechnungsformel für das Bestimmtheitsmaß. Die
alternative Berechnungsformel setzt die geforderte Kleinheit der
Residuenquadrate in Relation zur gesamten Quadratsumme. Die zur Konstruktion des
Bestimmtheitsmaßes verwendete Quadratsummenzerlegung kann als
„Streuungszerlegung“ interpretiert werden, bei der die „Gesamtstreuung“ in die
„erklärte Streuung“ und die „Reststreuung“ zerlegt wird.[A
5] Das Bestimmtheitsmaß ist als gerade als jener Anteil der
Gesamstreuung
zu deuten, der mit der Regressionsfunktion erklärt werden kann. Der unerklärte
Teil bleibt als Reststreuung zurück.
Das Bestimmtheitsmaß dient als Maßzahl zur Beurteilung der globalen Anpassungsgüte
eines Regressionsmodells. In der einfachen linearen Regression und der multiplen
linearen Regression entspricht das Bestimmtheitsmaß dem Quadrat des
Bravais-Pearson-Korrelationskoeffizienten
(siehe auch Abschnitt Als
quadrierter Korrelationskoeffizient). Dieser Umstand ist dafür
verantwortlich, dass das Bestimmtheitsmaß als
(lies: R Quadrat) oder
notiert wird. In deutschsprachiger Literatur findet sich auch der Buchstabe
als Bezeichnung für das Bestimmtheitsmaß. In den Anfängen der Statistik wurde
mit dem Buchstaben
ein Schätzer des Korrelationskoeffizienten der Grundgesamtheit
notiert und in der Regressionsanalyse
wird diese Notation noch heute verwendet.
Eigenschaften
Wertebereich des Bestimmtheitsmaßes
Mithilfe der obigen Definition können die Extremwerte für das
Bestimmtheitsmaß aufgezeigt werden. Für das Bestimmtheitsmaß gilt, dass es umso
näher am Wert
ist, je kleiner die Residuenquadratsumme
ist. Es wird maximal gleich
,
wenn
ist, also alle Residuen null sind. In diesem Fall ist die Anpassung an die Daten
perfekt, was bedeutet, dass für jede Beobachtung
ist und alle Beobachtungspunkte des Streudiagramms
auf der Regressionsgeraden liegen. Das Bestimmtheitsmaß nimmt hingegen den Wert
an, wenn
beziehungsweise
ist. Diese Gleichung besagt, dass die „nicht erklärte Streuung“ der „gesamten zu
erklärenden Streuung“ entspricht und die erklärenden
Variablen
somit keinen Beitrag zur Erklärung der Gesamtstreuung leisten. Die gesamte zu
erklärende Streuung wird in diesem Fall durch die Residuen hervorgerufen und die
Regressionsgleichung „erklärt“ gar nicht.
Aus der Betrachtung dieser beiden Fälle folgt
.
Wenn das Regressionsmodell kein Absolutglied enthält (es liegt ein homogenes
Regressionsmodell vor), kann das Bestimmtheitsmaß negativ werden (siehe
Abschnitt Einfache
lineare Regression durch den Ursprung).
Ebenfalls kann das Bestimmtheitsmaß negativ werden, wenn es auf simultane
Gleichungsmodelle angewendet wird, da in diesem Kontext
nicht notwendigerweise gleich
ist.
Als quadrierter Korrelationskoeffizient
Bei einer einfachen
linearen Regression (nur eine erklärende Variable)
entspricht das Bestimmtheitsmaß dem Quadrat
des Bravais-Pearson-Korrelationskoeffizienten
und lässt sich aus der Produktsumme
(Summe der Produkte der Abweichungen der Messwerte vom
jeweiligen Mittelwert
)
und den Quadratsummen
und
berechnen:
,
wobei der Kleinste-Quadrate-Schätzer
für die Steigung
der Quotient aus Produktsumme von
und
und Quadratsumme von
ist. In der einfachen linearen Regression ist
,
wenn
ist, d.h. die erklärende Variable steht zur Schätzung von
nicht zur Verfügung. Dies folgt aus der Tatsache, dass in der einfachen linearen
Regression
[A
6] gilt. In diesem Fall besteht das „beste“ lineare Regressionsmodell
nur aus dem Absolutglied
.
Das so definierte Bestimmtheitsmaß ist ebenfalls gleich null, wenn der
Korrelationskoeffizient
gleich null ist, da es in der einfachen linearen Regression dem quadrierten
Korrelationskoeffizienten zwischen
und
entspricht. Im Kontext der einfachen linearen Regression wird das
Bestimmtheitsmaß auch als einfaches Bestimmtheitsmaß bezeichnet. Bei der
Interpretation des einfachen Bestimmtheitsmaßes muss man vorsichtig sein, da es
u.U. schon deshalb groß ist, weil die Steigung
der Regressionsgeraden groß ist.
In der Realität hängen abhängige Variablen im Allgemeinen von mehr als einer erklärenden Variablen ab. Zum Beispiel ist das Gewicht eines Probanden nicht nur von dessen Alter, sondern auch von dessen sportlicher Betätigung und psychologischen Faktoren abhängig. Bei einer multiplen Abhängigkeit gibt man die Annahme der einfachen linearen Regression auf, bei der die abhängige Variable nur von einer erklärenden Variablen abhängt. Um eine mehrfache Abhängigkeit zu modellieren, benutzt man ein typisches multiples lineares Regressionsmodell
.
Hierbei ist
die Anzahl der zu schätzenden unbekannten Parameter und
die Anzahl der erklärenden Variablen. Zusätzlich zur Dimension der unabhängigen
Variablen wird auch eine zeitliche Dimension integriert, wodurch sich ein
lineares Gleichungssystem ergibt, was sich
in Vektor-Matrix-Form
darstellen lässt.
Im Gegensatz zur einfachen linearen Regression entspricht in der multiplen
linearen Regression das
dem Quadrat des Korrelationskoeffizienten zwischen den Messwerten
und den Schätzwerten
(für einen Beweis, siehe Matrixschreibweise),
also
.
Im Kontext der multiplen linearen Regression wird das Bestimmtheitsmaß auch
als mehrfaches bzw. multiples Bestimmtheitsmaß bezeichnet.
Aufgrund des oben aufgezeigten Zusammenhangs kann das multiple Bestimmtheitsmaß
als eine Maßzahl für die Anpassungsgüte der geschätzten Regressionshyperebene
an die Realisierungen
der Zufallsvariablen
angesehen werden. Es ist also ein Maß
des linearen Zusammenhangs zwischen
und
.
Hierarchisch geordnete Modelle
Sei der
der Vektor der erklärenden Variablen. Ferner wird angenommen, dass
in zwei Teilvektoren
und
partitioniert
wird, d.h.
.
Sei weiterhin
das volle Modell
und
und ein darin enthaltenes Teilmodell
.
Dann gilt
,
d.h. für hierarchisch
geordnete Modelle ist das Bestimmtheitsmaß des Teilmodells immer kleiner
oder gleich dem Bestimmtheitsmaß des vollen Modells.
Dies bedeutet, dass das Bestimmtheitsmaß mit zunehmender Anzahl der erklärenden
Variablen automatisch ansteigt, ohne dass sich dabei die Güte der Anpassung
signifikant verbessern muss.
Interpretation
.png)
Das Bestimmtheitsmaß lässt sich mit
multiplizieren, um es in Prozent anzugeben:
ist dann der prozentuale Anteil der Streuung
in
,
der durch das lineare
Modell „erklärt“ wird, und liegt daher zwischen:
(oder
): kein linearer Zusammenhang und
(oder
): perfekter linearer Zusammenhang.
Je näher das Bestimmtheitsmaß am Wert Eins liegt, desto höher ist die
„Bestimmtheit“ bzw. „Güte“ der Anpassung. Bei
ist der lineare Schätzer
im Regressionsmodell völlig unbrauchbar für die Vorhersage des Zusammenhangs
zwischen
und
(z.B. kann man das tatsächliche Gewicht der Person
überhaupt nicht mit dem Schätzer
vorhersagen). Ist
,
dann lässt sich die abhängige Variable
vollständig durch das lineare Regressionsmodell erklären. Anschaulich liegen
dann die Messpunkte
alle auf der (nichthorizontalen) Regressionsgeraden. Somit liegt bei diesem Fall
kein stochastischer Zusammenhang vor, sondern ein deterministischer.
Durch die Aufnahme zusätzlicher erklärender Variablen kann das
Bestimmtheitsmaß nicht sinken. Das Bestimmtheitsmaß hat die Eigenschaft, dass es
i.d.R. durch die Hinzunahme weiterer erklärender Variablen steigt
(),
was scheinbar die Modellgüte steigert und zum Problem der Überanpassung führen
kann. Das Bestimmtheitsmaß steigt durch die Hinzunahme weiterer erklärender
Variablen, da durch die Hinzunahme dieser der Wert der Residuenquadratsumme
sinkt. Auch wenn dem Modell irrelevante „erklärende Variablen“ hinzugefügt
werden, können diese zu Erklärung der Gesamtstreuung beitragen und den
R-Quadrat-Wert künstlich steigern. Da die Hinzunahme jeder weiteren
erklärenden Variablen mit einem Verlust eines Freiheitsgrads verbunden ist,
führt dies zu einer ungenaueren Schätzung. Wenn man Modelle mit einer
unterschiedlichen Anzahl erklärender Variablen und gleichen unabhängigen
Variablen vergleichen will, ist die Aussagekraft des Bestimmtheitsmaßes
begrenzt.
Um solche Modelle vergleichen zu können, wird ein „adjustiertes“
Bestimmtheitsmaß verwendet, welches zusätzlich die Freiheitsgrade berücksichtigt
(siehe auch Abschnitt Das
adjustierte Bestimmtheitsmaß).
Aus dem Bestimmtheitsmaß kann man im Allgemeinen nicht schließen, ob das angenommene Regressionsmodell dem tatsächlichen funktionalen Zusammenhang in den Messpunkten entspricht (siehe auch Abschnitt zu Grenzen und Kritik). Der Vergleich des Bestimmtheitsmaßes über Modelle hinweg ist nur sinnvoll, wenn eine gemeinsame abhängige Variable vorliegt und wenn die Modelle die gleiche Anzahl von Regressionsparametern und ein Absolutglied aufweisen. Da mit dem Bestimmtheitsmaß auch indirekt der Zusammenhang zwischen der abhängigen und den unabhängigen Variablen gemessen wird, ist es ein proportionales Fehlerreduktionsmaß.
In den Sozialwissenschaften
sind niedrige R-Quadrat-Werte in Regressionsgleichungen nicht
ungewöhnlich.
Bei Querschnittsanalysen
treten häufig niedrige R-Quadrat-Werte auf. Dennoch bedeutet ein kleines
Bestimmtheitsmaß nicht notwendigerweise, dass die
Kleinste-Quadrate-Regressionsgleichung unnütz ist. Es ist immer noch möglich,
dass die Regressionsgleichung ein guter Schätzer für den ceteris
paribus-Zusammenhang zwischen
und
ist. Ob die Regressionsgleichung ein guter Schätzer für den Zusammenhang von
und
ist hängt nicht direkt von der Größe des Bestimmtheitsmaßes ab.
Cohen und Cohen (1975) und Kennedy (1981) konnten zeigen, dass sich das Bestimmtheitsmaß graphisch mittels Venn-Diagrammen veranschaulichen lässt.
Konstruktion
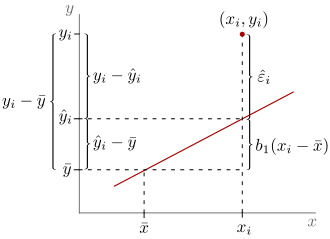
Ausgangspunkt für die Konstruktion des Bestimmtheitsmaßes ist die
Quadratsummenzerlegung, die als Streuungszerlegung interpretiert
werden kann. In Bezug auf
lässt sich
darstellen als
oder äquivalent
,
wobei
die Abweichung von
vom Mittelwert
und
die Restabweichung bzw. das Residuum darstellt. Die Gesamtabweichung
lässt sich also zerlegen in die erklärte Abweichung und das
Residuum. Die Gleichheit gilt auch dann noch, wenn man die Abweichungen
quadriert (Abweichungsquadrate bildet) und anschließend über alle Beobachtungen
summiert (Abweichungsquadratsummen, kurz: Quadratsummen bildet). Die totale
Quadratsumme bzw. die zu „erklärende“ Quadratsumme lässt sich in die
Quadratsumme der durch die Regressionsfunktion „erklärten“ Abweichungen vom
Gesamtmittel (durch das Modell „erklärte“ Quadratsumme) und die Residuenquadratsumme
(durch das Modell nicht „erklärte“ Quadratsumme) zerlegen. Die
Quadratsummenzerlegung ergibt somit
oder äquivalent dazu
.
Diese Zerlegung folgt in zwei Schritten. Im ersten Schritt wird eine Nullergänzung vorgenommen:
.
Im zweiten Schritt wurde die Eigenschaft benutzt, dass gewöhnliche
Residuen
vorliegen, die mit den geschätzten Werten unkorreliert
sind, d.h.
.
Dies kann so interpretiert werden, dass in der Schätzung bereits alle relevante
Information der erklärenden Variablen bezüglich der abhängigen Variablen
steckt.
Zudem wurde die Eigenschaft verwendet, dass – wenn das Modell das
Absolutglied enthält – die Summe
und damit der empirische Mittelwert der Residuen Null ist.
Dies folgt aus den verwendeten Schätzverfahren (Maximum-Likelihood-Schätzung
bei der klassischen
Normalregression oder Kleinste-Quadrate-Schätzung),
denn dort müssen die ersten
partiellen
Ableitungen der Residuenquadratsumme nach
gleich Null gesetzt werden um das Maximum bzw. Minimum zu finden, also für
:
bzw. für
mit
(siehe Algebraische
Eigenschaften). Werden die Regressionsparameter
mittels der Kleinste-Quadrate-Schätzung
geschätzt, dann wird der Wert für
automatisch maximiert, da die Kleinste-Quadrate-Schätzung die
Residuenquadratsumme minimiert.
Im Anschluss an die Zerlegung dividiert man die Quadratsummenzerlegungsformel durch die totale Quadratsumme und erhält damit
oder
.
Das Verhältnis der durch die Regression erklärten Quadratsumme zur gesamten Quadratsumme
wird Bestimmtheitsmaß der Regression genannt. Aus der Quadratsummenzerlegungsformel wird ersichtlich, dass man das Bestimmtheitsmaß auch als
darstellen kann. Wenn die obige Quadratsummenzerlegungsformel durch
den Stichprobenumfang
beziehungsweise durch die Anzahl
der Freiheitsgrade
dividiert wird, erhält man die Varianzzerlegungsformel:
.
Die Varianzzerlegung stellt eine additive Zerlegung der Varianz der abhängigen
Variablen (totale Varianz bzw. Gesamtvarianz)
in die Varianz der Schätzwerte
(erklärte Varianz) und die nicht erklärte Varianz
(auch Residualvarianz
genannt) dar.
Hierbei entspricht die Residualvarianz dem
Maximum-Likelihood-Schätzer
für die Varianz der Störgrößen
.
Aufgrund der Varianzzerlegung lässt sich das Bestimmtheitsmaß auch als
darstellen und wie folgt interpretieren: Das Bestimmtheitsmaß gibt an, wie viel
Varianzaufklärung alle erklärenden
Variablen
an der Varianz der abhängigen Variablen
leisten. Diese Interpretation ist jedoch nicht ganz korrekt, da die
Quadratsummen eigentlich unterschiedliche Freiheitsgrade aufweisen. Diese
Interpretation trifft eher auf das adjustierte
Bestimmtheitsmaß zu, da hier die erwartungstreuen Varianzschätzer ins
Verhältnis gesetzt werden.
Im Gegensatz zur Varianzaufklärung beim Bestimmtheitsmaß kann man bei der
Varianzaufklärung in der Hauptkomponenten-
und Faktorenanalyse
jeder Komponente bzw. jedem Faktor seinen Beitrag zur Aufklärung der gesamten
Varianz zuordnen.
Einfache lineare Regression durch den Ursprung
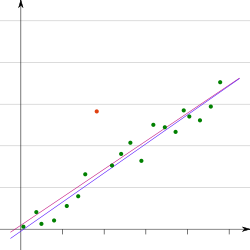
Im Fall der einfachen
linearen Regression durch den Ursprung/Regression ohne Absolutglied (das
Absolutglied
wird nicht in die Regression miteinbezogen und daher verläuft die
Regressionsgleichung durch den Koordinatenursprung)
lautet die konkrete empirische Regressionsgerade
,
wobei die Notation
benutzt wird um von der allgemeinen Problemstellung der Schätzung eines
Steigungsparameters mit Hinzunahme eines Absolutglieds zu unterscheiden.
Auch in einer einfachen linearen Regression durch den Ursprung lässt sich die
Kleinste-Quadrate-Schätzung anwenden. Sie liefert für die Steigung
.
Dieser Schätzer für den Steigungsparameter
entspricht dem Schätzer für den Steigungsparameter
,
dann und nur dann wenn
.
Wenn für das wahre Absolutglied
gilt, ist
ein verzerrter
Schätzer für den wahren Steigungsparameter
.
Wenn in eine Regressionsgleichung kein Absolutglied hinzugenommen wird, nimmt
der aus der obigen Quadratsummenzerlegungsformel entnommene Ausdruck
nicht den Wert Null an. Daher ist die oben angegebene
Quadratsummenzerlegungsformel in diesem Fall nicht gültig. Wenn das Modell der
Regression durch den Ursprung eine hinreichend schlechte Anpassung an die Daten
liefert (d.h. die Daten variieren mehr um die Regressionslinie als um
),
was in
resultiert und man die allgemeine
Definition des Bestimmtheitsmaßes
anwendet, dann führt dies zu einem negativen Bestimmtheitsmaß. Nach dieser
Definition kann
also negativ werden. Ein negatives Bestimmtheitsmaß bedeutet dann, dass das
empirische Mittel der abhängigen Variablen
eine bessere Anpassung an die Daten liefert als wenn man die erklärenden
Variablen
zur Schätzung benutzen würde.
Um ein negatives Bestimmtheitsmaß zu vermeiden wird eine modifizierte Form der
Quadratsummenzerlegung angegeben:
oder äquivalent dazu
.
Diese modifizierte Form der Quadratsummenzerlegung wird auch nicht
korrigierte Quadratsummenzerlegung genannt, da die erklärte und die totale
Quadratsumme nicht um den empirischen Mittelwert „korrigiert“ bzw.
„zentriert“
werden. Wenn man statt dem gewöhnlichen
und
die modifizierten Quadratsummen
und
benutzt, ist das Bestimmtheitsmaß gegeben durch
.
Dieses Bestimmtheitsmaß ist strikt nichtnegativ und wird – da es auf der nicht korrigierten Quadratsummenzerlegung aufbaut, bei der nicht um den empirischen Mittelwert „zentriert“ wird – auch als unzentriertes Bestimmtheitsmaß bezeichnet. Zur Abgrenzung wird das konventionelle Bestimmtheitsmaß auch als zentriertes Bestimmtheitsmaß bezeichnet. Bei einer Regression durch den Ursprung wird daher die modifizierte Form der Quadratsummenzerlegungsformel verwendet.
Rechenbeispiel
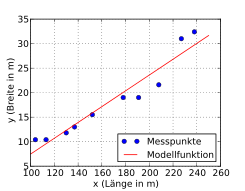
Folgendes Beispiel soll die Berechnung des Bestimmtheitsmaßes zeigen. Es wurden zufällig zehn Kriegsschiffe ausgewählt und bezüglich ihrer Länge und Breite (in Metern) analysiert. Es soll untersucht werden, ob die Breite eines Kriegsschiffs möglicherweise in einem festen Bezug zur Länge steht.
Das Streudiagramm
lässt einen linearen Zusammenhang zwischen Länge und Breite eines Schiffs
vermuten. Eine mittels der Kleinste-Quadrate-Schätzung
durchgeführte einfache lineare Regression ergibt für das Absolutglied
und die Steigung
(für die Berechnung der Regressionsparameter siehe Beispiel
mit einer Ausgleichsgeraden). Die geschätzte Regressionsgerade lautet somit
.
Die Gleichung stellt die geschätzte Breite
als Funktion der Länge
dar. Die Funktion zeigt, dass die Breite der ausgewählten Kriegsschiffe grob
einem Sechstel ihrer Länge entspricht.
| Kriegsschiff | Länge (m) | Breite (m) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 208 | 21,6 | 3,19 | 10,1761 | 24,8916 | −3,2916 | 10,8347 |
| 2 | 152 | 15,5 | −2,91 | 8,4681 | 15,8625 | −0,3625 | 0,1314 |
| 3 | 113 | 10,4 | −8,01 | 64,1601 | 9,5744 | 0,8256 | 0,6817 |
| 4 | 227 | 31,0 | 12,59 | 158,5081 | 27,9550 | 3,045 | 9,2720 |
| 5 | 137 | 13,0 | −5,41 | 29,2681 | 13,4440 | −0,4440 | 0,1971 |
| 6 | 238 | 32,4 | 13,99 | 195,7201 | 29,7286 | 2,6714 | 7,1362 |
| 7 | 178 | 19,0 | 0,59 | 0,3481 | 20,0546 | −1,0546 | 1,1122 |
| 8 | 104 | 10,4 | −8,01 | 64,1601 | 8,1233 | 2,2767 | 5,1835 |
| 9 | 191 | 19,0 | 0,59 | 0,3481 | 22,1506 | −3,1506 | 9,9265 |
| 10 | 130 | 11,8 | −6,61 | 43,6921 | 12,3154 | −0,5154 | 0,2656 |
| Σ | 1678 | 184,1 | 574,8490 | 0,0000 | 44,7405 | ||
| Σ/n | 167,8 | 18,41 | 57,48490 | 0,0000 | 4,47405 |
Aus der Tabelle lässt sich erkennen, dass der Gesamtmittelwert der Breite
beträgt, die totale Quadratsumme der Messwerte
beträgt und die Residuenquadratsumme
beträgt. Daher ergibt sich das Bestimmtheitsmaß zu
,
d.h. circa
der Streuung in der Kriegsschiffsbreite kann durch die lineare Regression
von Kriegsschiffsbreite auf Kriegsschiffslänge „erklärt“ werden. Das Komplement
des Bestimmtheitsmaßes
wird auch Unbestimmtheitsmaß (auch Koeffizient der
Nichtdetermination oder Alienationskoeffizient, von lateinisch alienus
„fremd“, „unbekannt“) genannt. Bestimmtheits- und Unbestimmtheitsmaß addieren
sich jeweils zu
.
Das Unbestimmtheitsmaß
sagt im vorliegenden Beispiel aus, dass knapp
der Streuung in der Breite „unerklärt“ bleiben. Hier könnte man z.B. nach
weiteren Faktoren suchen, welche die Breite eines Kriegsschiffes beeinflussen
und sie in die Regressionsgleichung mit aufnehmen.
Vergleich mit dem Standardfehler der Regression
Die „Qualität“ der Regression kann auch mithilfe des geschätzten
Standardfehlers der
Residuen (engl. residual standard error) beurteilt werden, der zum
Standardoutput der meisten statistischen Programmpakete gehört. Der geschätzte
Standardfehler der Residuen gibt an, mit welcher Sicherheit die Residuen
den wahren Störgrößen
näherkommen. Die Residuen sind somit eine Approximation
der Störgrößen. Der geschätzte Standardfehler der Residuen ist mit dem
Bestimmtheitsmaß und dem adjustierten Bestimmtheitsmaß vergleichbar und ähnlich
zu interpretieren. Der geschätzte Standardfehler der Residuen, der sich aus der
obigen Tabelle berechnen lässt, ergibt einen Wert von:
.
Es ist jedoch zu beachten, dass
eine verzerrte
Schätzung der wahren Varianz der Störgrößen
ist, da der verwendete Varianzschätzer
nicht erwartungstreu
ist. Wenn man berücksichtigt, dass man durch die Schätzung der beiden
Regressionsparameter
und
zwei Freiheitsgrade verliert und somit statt durch den Stichprobenumfang
durch die Anzahl
der Freiheitsgrade
dividiert, erhält man das „mittlere
Residuenquadrat“
und damit die
erwartungstreue
Darstellung:
.
Die Darstellung ist unverzerrt, da sie durch Einbezug der Freiheitsgrade der
Varianzschätzer, wegen ,
unter den Gauß-Markow-Annahmen
erwartungstreu ist (siehe auch Schätzer
für die Varianz der Störgrößen).
Die unverzerrte Darstellung
wird im Regressionsoutput statistischer
Software oft auch als Standardfehler der Schätzung oder
Standardfehler
der Regression (engl. standard error of the regression, kurz:
SER) bezeichnet.[A
7] Der Standardfehler der Regression wird als Quadratwurzel des
mittleren Residuenquadrats berechnet und ist ein eigenständiges Modellgütemaß.
Er gibt an, wie groß im Durchschnitt die Abweichung der Messwerte von der
Regressionsgerade ausfällt. Je größer der Standardfehler der Regression, desto
schlechter beschreibt die Regressionsgerade die Verteilung der Messwerte. Der
Standardfehler der Regression ist in der Regel kleiner als der Standardfehler
der Zielgröße
.
Das Bestimmtheitsmaß wird häufiger angegeben als der Standardfehler der
Residuen, obwohl der Standardfehler der Residuen bei der Bewertung
Anpassungsgüte möglicherweise aussagekräftiger ist.
Missverständnisse, Grenzen und Kritik
Missverständnisse
Neben den Vorteilen des Bestimmtheitsmaßes (es ist eine dimensionslose Größe,
hat eine einfache Interpretation und liegt stets zwischen
und
)
wird das Bestimmtheitsmaß immer wieder kritisiert und falsch angewendet:
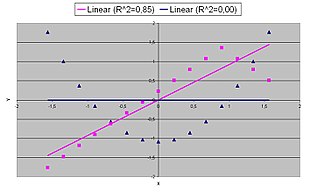
- Übliche Missverständnisse sind:
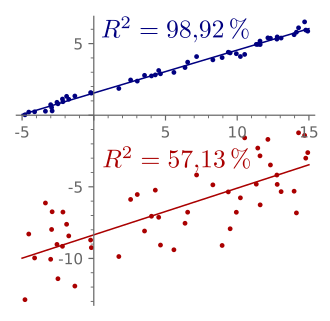
- Bei einem hohen Bestimmtheitsmaß für einen Schätzer
könne man folgern, dass der tatsächliche Zusammenhang linear sei. Die pinken Daten in der Grafik wurden mit einer nichtlinearen Funktion generiert:[A 8]
- Bei einem hohen Bestimmtheitsmaß für einen Schätzer
-
-
- Durch die Betragsfunktion
im Term nimmt die Funktion
an der Stelle
ihr Maximum
an. Für höhere Werte von
fällt die Funktion dann streng monoton mit der Steigung
. Damit wäre der tatsächliche Zusammenhang in den Daten auch bei dem hohen Bestimmtheitsmaß nach Konstruktion natürlich nicht linear. Dennoch legt das hohe Bestimmtheitsmaß nahe, dass es sich um einen linearen Zusammenhang handelt.
- Ein hohes Bestimmtheitsmaß gebe an, dass die geschätzte Regressionslinie überall eine gute Approximation an die Daten darstellt; die pinken Daten legen auch hier etwas anderes nahe.
- Ein Bestimmtheitsmaß nahe bei Null zeige an, dass es keinen Zusammenhang
zwischen der abhängigen und den unabhängigen Variablen gebe. Die blauen
Daten in der Grafik wurden mit der folgenden quadratischen
Funktion
generiert und besitzen daher einen deterministischen funktionalen Zusammenhang, der allerdings nicht linear ist[A 9]
-
.
- Obwohl das Bestimmtheitsmaß gleich Null ist, lässt sich nicht daraus
schließen, dass es keinen Zusammenhang zwischen der abhängigen und
den unabhängigen Variablen für die konstruierten Datenpunkte gibt. Eine Regressionsanalyse
für nichtlineare Fälle verallgemeinert die lineare Regression auf andere
Klassen von Funktionen und mehrdimensionale Definitionsbereiche
von
.
- Wählt man aus den Daten mit quadratischem Zusammenhang (Parabel
) nur die Datenpunkte mit positivem
-Werten aus, kann auch das Bestimmtheitsmaß sehr hoch sein und bei einem nach Konstruktion der Daten gegebenen quadratischem Zusammenhang durch
in den Messdaten dennoch eine lineare Modellannahme suggerieren (z.B. wenn man nur die Daten aus der Parabel wählt, in der die Funktion positive Steigung besitzt).
-
Grenzen und Kritik
-
- Das Bestimmtheitsmaß zeigt zwar die „Qualität“ der linearen Approximation, jedoch nicht, ob das Modell richtig spezifiziert wurde. Zum Beispiel kann ein nichtlinearer Zusammenhang bei einer der unabhängigen Variablen vorliegen. In einem solchen Fall können die unabhängigen Variablen unentdeckte Erklärungskraft enthalten, auch dann wenn das Bestimmtheitsmaß einen Wert nahe bei Null aufweist. Modelle, die mittels der Kleinste-Quadrate-Schätzung geschätzt wurden, werden daher die höchsten R-Quadrat-Werte aufweisen.
- (Korrelation/Kausaler
Zusammenhang) Das Bestimmtheitsmaß sagt nichts darüber aus, ob die
unabhängige Variable
der Grund (die kausale Ursache) für die Änderungen in
sind. Zum Beispiel kann das Bestimmtheitsmaß zwischen der Anzahl der Störche
und der Anzahl der neugeborenen Kinder
in untersuchten Gebieten
hoch sein. Ein direkter kausaler Zusammenhang zwischen Störchen und Neugeborenen ist jedoch biologisch ausgeschlossen (siehe Scheinkorrelation.
- Das Bestimmtheitsmaß sagt nichts über die statistische Signifikanz des ermittelten Zusammenhangs und der einzelnen erklärenden Variablen aus. Um diesen zu ermitteln muss die Stichprobengröße bekannt sein und ein Signifikanztest durchgeführt werden.
- Das Bestimmtheitsmaß macht keine Aussage über Multikollinearität
zwischen den unabhängigen Variablen
. Multikollinearität kann z.B. mithilfe des Varianzinflationsfaktors identifiziert werden (siehe auch Abschnitt Interpretation der Varianz der Regressionsparameter).
- Es zeigt nicht an, ob eine Verzerrung durch ausgelassene Variablen (engl. omitted variable bias) vorliegt.
- Es macht keine Aussage, ob eine Transformation der Daten die Erklärungskraft der Regression verbessert.
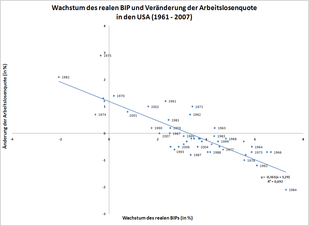
- Ein Nachteil des Bestimmtheitsmaßes ist die Empfindlichkeit gegenüber Trends: Wenn sich eine exogene Variable parallel zu einer erklärenden entwickelt, werden unabhängig von der wahren Erklärungskraft des Modells hohe R-Quadrat-Werte ausgewiesen.
- Zusammenfassend ist ein hohes Bestimmtheitsmaß kein Beweis für ein
„gutes“ Modell und ein niedriges Bestimmtheitsmaß bedeutet nicht, dass es
sich um ein „schlechtes“ Modell handelt. Dies wird anhand des Anscombe-Beispiels
(1973)
deutlich. Anscombe zeigte auf der Basis von vier verschiedenen Datensätzen,
dass ein in allen vier Fällen relativ hohes Bestimmtheitsmaß von
nichts darüber aussagt, ob der wahre Zusammenhang zwischen zwei Variablen richtig erfasst worden ist.
Geschichte


Die Grundlage des Bestimmtheitsmaßes stellt die Regressionsanalyse und der Korrelationskoeffizient dar. Der britische Naturforscher Sir Francis Galton (1822–1911) begründete in den 1870er-Jahren die Regressionsanalyse. Er war – wie auch sein Cousin Charles Darwin – ein Enkel von Erasmus Darwin. Galton war durch seine starke Leidenschaft Daten jeglicher Art zu sammeln bekannt. Beispielsweise sammelte er Daten der Samen von Platterbsen. Beim Vergleich der Durchmesser der Samen konstruierte er das, was heute allgemein als Korrelationsdiagramm bekannt ist. Den bei dieser Tätigkeit von ihm entdeckte Zusammenhang taufte er zunächst „Reversion“ (Umkehrung); später entschied er sich jedoch für die Bezeichnung „Regression“. Bei der Analyse der Samen entdeckte er das Phänomen der Regression zur Mitte, nach dem – nach einem extrem ausgefallenen Messwert – die nachfolgende Messung wieder näher am Durchschnitt liegt: Der Mediandurchmesser der Nachkommen der größeren Samen war kleiner als der Mediandurchmesser der Samen der Eltern (vice versa). In seine Korrelationsdiagramme zeichnete er eine Trendlinie ein, für die er als Steigung den Korrelationskoeffizienten verwendete.
Die Bezeichnung „Varianz“ wurde vom Statistiker Ronald Fisher (1890–1962) in seinem 1918 veröffentlichtem Aufsatz mit dem Titel Die Korrelation zwischen Verwandten in der Annahme der Mendelschen Vererbung (Originaltitel: The Correlation between Relatives on the Supposition of Mendelian Inheritance) eingeführt. Fisher war einer der bedeutendsten Statistiker des 20. Jahrhunderts und ist für seine Beiträge zur Evolutionstheorie berühmt. Ebenso ist er für die Entdeckung der Streuungszerlegung (engl. analysis of variance) bekannt, die die Grundlage für das Bestimmtheitsmaß darstellt. Die – eng in Verbindung mit dem Bestimmtheitsmaß stehende – F -Statistik ist ebenfalls nach ihm benannt. Karl Pearson (1857–1936), der Begründer der Biometrie, lieferte schließlich eine formal-mathematische Begründung für den Korrelationskoeffizienten, dessen Quadrat dem Bestimmtheitsmaß entspricht.
Das Bestimmtheitsmaß wurde in den folgenden Jahren stark kritisiert. Dies geschah auch da es die Eigenschaft hat, dass es umso größer wird, je größer die Zahl der unabhängigen Variablen ist. Dies ist unabhängig davon, ob die zusätzlichen erklärenden Variablen einen Beitrag zur Erklärungskraft liefern. Um diesen Umstand Rechnung zu tragen, schlug der Ökonometriker Henri Theil 1961 das adjustierte Bestimmtheitsmaß (auch bereinigtes, korrigiertes oder angepasstes Bestimmtheitsmaß genannt) vor. Dies berücksichtigt, dass die Hinzunahme jeder weiteren erklärenden Variablen mit einem Verlust eines Freiheitsgrads verbunden ist, wurde jedoch von Rinne (2004) in der Hinsicht kritisiert, dass das Auswahlkriterium den Verlust an Freiheitsgraden mit wachsender Anzahl an erklärenden Variablen nicht ausreichend bestraft.
Das adjustierte Bestimmtheitsmaß
Definition
Das Bestimmtheitsmaß
hat die Eigenschaft, dass es umso größer wird, je größer die Zahl der
unabhängigen Variablen ist. Dies ist unabhängig davon, ob die zusätzlichen
unabhängigen Variablen einen Beitrag zur Erklärungskraft liefern. Daher ist es
ratsam, das adjustierte (freiheitsgradbezogene) Bestimmtheitsmaß (auch
bereinigtes, korrigiertes oder angepasstes Bestimmtheitsmaß genannt) zu Rate zu
ziehen. Das adjustierte Bestimmtheitsmaß nach Theil wird mit
(lies: R Quer Quadrat) oder
bzw.
notiert. Man erhält das adjustierte Bestimmtheitsmaß, wenn an Stelle der
Quadratsummen die mittleren
Abweichungsquadrate (englisch
mean squares)
und
verwendet werden:
.
Hierbei ist
das „mittlere Residuenquadrat“
(Mittleres Quadrat der Residuen, kurz:
MQR) und
das „mittlere Gesamtabweichungsquadrat“ (Mittleres Quadrat der
Totalen Abweichungen, kurz: MQT). Das adjustierte
Bestimmtheitsmaß modifiziert die Definition des Bestimmtheitsmaßes, indem es den
Quotienten
mit dem Faktor
multipliziert.
Alternativ lässt sich das adjustierte Bestimmtheitsmaß algebraisch äquivalent
darstellen als
.
Definitionsgemäß ist das adjustierte Bestimmtheitsmaß für mehr als eine
erklärende Variable stets kleiner als das unadjustierte.
Beim adjustierten Bestimmtheitsmaß wird die Erklärungskraft des Modells,
repräsentiert durch ,
ausbalanciert mit der Komplexität des Modells, repräsentiert durch
,
die Anzahl der Parameter. Je komplexer das Modell ist, desto mehr „bestraft“ das
adjustierte Bestimmtheitsmaß jede neu hinzugenommene erklärende Variable. Das
adjustierte Bestimmtheitsmaß steigt nur, wenn
ausreichend steigt, um den gegenläufigen Effekt des Quotienten
auszugleichen und kann ebenfalls sinken (
).
Auf diese Weise lässt sich
als Entscheidungskriterium bei der Auswahl zwischen zwei alternativen Modellspezifikationen
(etwa einem restringierten
und einem unrestringierten
Modell) verwenden. Das adjustierte Bestimmtheitsmaß kann negative Werte
annehmen und ist kleiner als das unbereinigte, außer falls
und damit auch
ist. Als Ergebnis daraus folgt
.
Das adjustierte Bestimmtheitsmaß nähert sich mit steigendem Stichprobenumfang
dem unadjustierten Bestimmtheitsmaß. Dies liegt daran, dass bei fixer Anzahl der
erklärenden Variablen für den Grenzwert
für den Korrekturfaktor bzw. Strafterm gilt
.
In der Praxis ist es nicht zu empfehlen das adjustierte Bestimmtheitsmaß zu
verwenden, da die „Bestrafung“ für neu hinzugefügte erklärende Variablen zu
klein erscheint. Man kann zeigen, dass das
schon steigt, wenn eine erklärende Variable mit einem t-Wert
größer als Eins in das Modell inkludiert wird.
Aus diesem Grund wurden weitere Kriterien (sogenannte Informationskriterien)
wie z.B. das Akaike-Informationskriterium
und das bayessche
Informationskriterium zur Modellauswahl
entwickelt, die ebenfalls der Idee von Ockhams
Rasiermesser folgen, dass ein Modell nicht unnötig komplex sein soll.
Konstruktion
Aus der allgemeinen Definition von
folgt, dass
.
Wir wissen jedoch, dass
und
verzerrte
Schätzer für die wahre Varianz der Störgrößen
und die der Messwerte
sind. Aus dieser Tatsache wird deutlich, dass es sich beim multiplen
Bestimmtheitsmaß
um eine Zufallsvariable handelt: Das multiple Bestimmtheitsmaß kann man als Schätzfunktion für
das unbekannte Bestimmtheitsmaß in der Grundgesamtheit
[A
10] (lies: rho Quadrat) betrachten. Dieses
ist gegeben durch
und ist der Anteil der Streuung in
in der Grundgesamtheit,
der durch die erklärenden Variablen „erklärt“ wird.
Dividiert man die jeweiligen Quadratsummen durch ihre Freiheitsgrade, so erhält
man jeweils das durchschnittliche
Abweichungsquadrat (Varianz):
und
.
Die Varianzen
und
sind erwartungstreue
Schätzer für die wahre Varianz der Störgrößen
und die der Messwerte
.
Setzt man nun bei
oben und unten die unverzerrten Schätzer ein, so erhält man das adjustierte
Bestimmtheitsmaß:
.
Durch algebraische Umformungen erhält man schließlich
.
Das adjustierte Bestimmtheitsmaß
entspricht also dem um die unverzerrten Komponenten adjustiertem
Bestimmtheitsmaß
.
Oft wird das adjustierte Bestimmtheitsmaß auch korrigiertes
Bestimmtheitsmaß genannt. Dies ist keine gute Bezeichnung, da sie impliziert
dass
in einer Weise „besser“ ist als
,
um das Bestimmtheitsmaß in der Grundgesamtheit
zu schätzen. Dies ist aber nicht der Fall, da das Verhältnis zweier unverzerrter
Schätzer kein unverzerrter Schätzer ist.
Auch die Bezeichnung „adjustiertes R-Quadrat“ kann irreführend sein, da
wie in obiger Formel nicht als das Quadrat irgendeiner Quantität berechnet
wird.
Matrixschreibweise
Das Bestimmtheitsmaß
In der multiplen linearen Regression, mit dem multiplen linearen Modell in Matrixschreibweise
beziehungsweise in Kurzform
,
ergibt sich das Bestimmtheitsmaß durch die korrigierte Quadratsummenzerlegung (um den Mittelwert bereinigte Quadratsummenzerlegung)
.
Die Bezeichnung „korrigiert“ hebt hervor, dass man die Summe über alle
Beobachtungen der quadrierten Werte nimmt, nachdem um den Mittelwert
„korrigiert“ wurde. Hierbei ist
ein Vektor mit
den Elementen
und
ist definiert durch
,
wobei
den -->Kleinste-Quadrate-Schätzvektor
darstellt.
Das Bestimmtheitsmaß ist dann gegeben durch:
Häufig findet sich auch die algebraisch äquivalente Darstellung
.
oder
.
Die letzte Gleichheit ergibt sich aus dem Umstand, dass sich
aus der linksseitigen Multiplikation von
mit der Prädiktionsmatrix
ergibt. Die Berechnung des Bestimmtheitsmaßes lässt sich in folgender Tafel
der Varianzanalyse
zusammenfassen:
| Variationsquelle | Abweichungsquadratsumme | Anzahl der Freiheitsgrade | Mittleres Abweichungsquadrat |
|---|---|---|---|
| Regression (erklärt) | |||
| Residuen (unerklärt) | |||
| Gesamt | |||
| Bestimmtheitsmaß |
Falls das lineare Modell das Absolutglied enthält, dann entspricht der empirische Mittelwert der Schätzwerte dem der beobachteten Messwerte, wegen
,
wobei
die, aus Einsen bestehende, erste Spalte der Datenmatrix
darstellt. Es wurde die Eigenschaft benutzt, dass der Vektor der KQ-Residuen und
der Vektor der erklärenden Variablen orthogonal und damit unkorreliert sind,
d.h es gilt
(siehe auch, algebraische
Eigenschaften der Kleinste-Quadrate-Schätzer).
Darstellung mittels Projektionsmatrix
Die Quadratsummenzerlegung und das Bestimmtheitsmaß lassen sich ebenfalls
mittels einer speziellen idempotenten
und symmetrischen
-Projektionsmatrix
darstellen,
die den Vektor
mit den Elementen
in den Vektor Abweichungen
mit Elementen
transformiert. Die linksseitige
Multiplikation von
mit
zentriert den Vektor
.
Daher wird diese Matrix auch als zentrierende
Matrix bezeichnet. Die totale Quadratsumme lässt sich also mittels der
zentrierenden Matrix auch darstellen als
.
Analog dazu lässt sich die Quadratsumme der Schätzwerte
schreiben als
und die Residuenquadratsumme als
.
Dadurch erhält man die Quadratsummenzerlegung als
wobei sich zeigen lässt, dass für die Streuung der Messwerte und die der
Schätzwerte folgender Zusammenhang gilt: .
Mithilfe dieses Zusammenhangs kann man zeigen, dass das multiple
Bestimmtheitsmaß dem Quadrat des Korrelationskoeffizienten zwischen
und
entspricht:
| Beweis |
|
|
Die Notation
für die Matrix
rührt daher, dass die residuenerzeugende
Matrix
– wobei
die Prädiktionsmatrix
darstellt – für den Fall, dass
der Matrix
entspricht. Die Matrix
ist also ein Spezialfall der residuenerzeugenden Matrix.
Das adjustierte Bestimmtheitsmaß
Man kann zeigen, dass die Veränderung des Bestimmtheitsmaßes, wenn eine
zusätzliche Variable
der Regression hinzugefügt wird
.
beträgt. Folglich kann das Bestimmtheitsmaß durch die Aufnahme zusätzlicher
erklärender Variablen nicht sinken. Hierbei stellt
das Bestimmtheitsmaß in der Regression von
auf
und einer zusätzlichen Variable
dar.
ist das Bestimmtheitsmaß für die Regression von
auf
alleine und
ist die partielle Korrelation zwischen
und
,
wenn man für
kontrolliert.
Wenn man immer weitere Variablen in das Model hinzufügt, wird der
R-Quadrat-Wert weiter ansteigen, bis hin zur oberen Grenze
.
Daher sollte das adjustierte Bestimmtheitsmaß herangezogen werden, das die
Aufnahme jeder neu hinzugenommenen erklärenden Variable „bestraft“.
In Matrixschreibweise ist das adjustierte Bestimmtheitsmaß gegeben durch den Quotienten aus dem „mittleren Residuenquadrat“ und dem „mittleren Quadrat der totalen Abweichungen“:
,
wobei
und
die unverzerrten Schätzer für die Varianzen von
und
darstellen.
Bestimmtheitsmaß bei Heteroskedastizität
Wenn die Anpassung durch die verallgemeinerte Kleinste-Quadrate-Schätzung erfolgt, können alternative Versionen des Bestimmtheitsmaßes entsprechend diesem statistischen Rahmenwerk berechnet werden, während das „einfache“ Bestimmtheitsmaß immer noch nützlich sein kann, da es einfacher zu interpretieren ist. Das Bestimmtheitsmaß bei vorliegen von Heteroskedastizität ist durch die gewichteten Summen der Abweichungsquadrate wie folgt definiert
,
wobei
die „gewichtete Residuenquadratsumme“ (englisch
weighted sum of squares residual, kurz: WSSR) und
die „gewichtete totale Quadratsumme“ (englisch
weighted sum of squares total, kurz: WSST) darstellt.
Im verallgemeinerten
linearen Regressionsmodell, also bei Vorliegen einer nichtskalaren Kovarianzmatrix der
Störgrößen
mit der Gewichtsmatrix
,
ist
gegeben durch:
,
wobei
den verallgemeinerten Kleinste-Quadrate-Schätzer darstellt.
Interpretation der Varianz der Regressionsparameter
Die Kovarianzmatrix
des Kleinste-Quadrate-Schätzvektors
ist gegeben durch
.[A
11] Die Diagonalelemente
dieser Kovarianzmatrix stellen die Varianzen
der jeweiligen Regressionsparameter dar. Es kann gezeigt werden, dass sich die
Varianzen auch darstellen lassen als
,
wobei
das Bestimmtheitsmaß einer Hilfsregression
ist, bei der die erklärende Variable
(hier als abhängige Variable) auf alle anderen erklärenden Variablen (inkl.
Absolutglied) regressiert wird. Je größer ceteris
paribus die lineare
Abhängigkeit einer erklärenden Variablen
mit anderen erklärenden Variablen ist (Multikollinearität,
gemessen durch
,
desto größer ist die Varianz. Im Extremfall
geht die Varianz gegen Unendlich.
Diese Varianzformel liefert mithilfe der Varianzinflationsfaktors
ebenfalls ein Diagnosewerkzeug, um den Grad der Multikollinearität zu messen.
Der Varianzinflationsfaktor quantifiziert einen Anstieg der Varianz von
aufgrund der linearen Abhängigkeit von
mit den restlichen erklärenden Variablen. Je größer die Korrelation zwischen
und den anderen erklärenden Variablen ist, desto größer ist
und damit der Varianzinflationsfaktor.
Mithilfe des Standardfehlers der Residuen, lassen sich Konfidenzintervalle
konstruieren. Ersetzt man bei der Standardabweichung des jeweiligen
Parameterschätzers
das unbekannte
durch das bekannte
ergibt sich der
Standardfehler
des Regressionskoeffizienten
durch
.
Die Größe der Standardfehler der geschätzten Regressionsparameter hängt also von der Residualvarianz, der Abhängigkeit der erklärenden Variablen untereinander und der Streuung der jeweiligen erklärenden Variablen ab.
R-Quadrat-Schreibweise der F-Statistik
Die allgemeine Form der F-Statistik ist definiert durch den relativen Zuwachs in der Residuenquadratsumme beim Übergang vom unrestringierten zum restringierten Modell
,
wobei
die Anzahl der zu testenden Restriktionen darstellt. Beim Testen von
Restriktionen ist es oft von Vorteil eine Darstellung der F-Statistik zu
haben, bei der die Bestimmtheitsmaße des restringierten Modells und des
unrestringierten Modells miteinbezogen werden. Ein Vorteil dieser Darstellung
ist, dass das die Residuenquadratsumme sehr groß und deren Berechnung damit
umständlich sein kann. Das Bestimmtheitsmaß dagegen liegt immer zwischen
und
.
Die R-Quadrat-Schreibweise der F-Statistik ist gegeben durch
,
wobei der Umstand genutzt wurde, dass für die Residuenquadratsumme des restringierten und des unrestringierten Modells gilt
und
.
Da das Bestimmtheitsmaß im Gegensatz zu Residuenquadratsumme in jedem Regressionsoutput ausgegeben wird, kann man leicht die Bestimmtheitsmaße des restringierten Modells und des unrestringierten Modells benutzen, um auf Variablenexklusion zu testen.
Test auf Gesamtsignifikanz eines Modells
Der globale F-Test prüft, ob mindestens eine Variable einen
Erklärungsgehalt für das Modell liefert. Falls diese Hypothese verworfen wird,
ist das Modell nutzlos. Dieser Test lässt sich so interpretieren, als würde man
die gesamte Anpassungsgüte der Regression, also das Bestimmtheitsmaß
der Regression, testen. Die Null-
und die Alternativhypothese
lauten:
gegen
und die Teststatistik dieses Tests ist gegeben durch
.
Das Modell unter der Nullhypothese
ist dann das sogenannte Nullmodell
(Modell, das nur aus einer Regressionskonstanten
besteht). Die Teststatistik
ist unter der Nullhypothese
F-verteilt mit
und
Freiheitsgraden.[A
12] Überschreitet der empirische F-Wert bei einem a priori
festgelegten Signifikanzniveau
den kritischen
F-Wert
(das
-Quantil
der F-Verteilung mit
und
Freiheitsgraden) so verwirft man die Nullhypothese, dass alle Steigungsparameter
des Modells gleich null sind. Das Bestimmtheitsmaß ist dann ausreichend groß und
mindestens eine erklärende Variable trägt vermutlich genügend Information zur
Erklärung der abhängigen Variablen bei. Es ist naheliegend, bei hohen
F-Werten die Nullhypothese zu verwerfen, da ein hohes Bestimmtheitsmaß zu
einem hohen F-Wert führt. Wenn der Wald-Test für eine oder mehrere
erklärende Variablen die Nullhypothese ablehnt, dann kann man davon ausgehen,
dass die zugehörigen Regressionsparameter ungleich Null sind, so dass die
Variablen in das Modell mit einbezogen werden sollten.
Es kann gezeigt werden, dass unter der obigen Nullhypothese sich für das Bestimmtheitsmaß im Mittel
ergibt.
Daraus folgt, dass wenn ,
dann ist
,
d.h. die bloße Größe des R-Quadrat-Wertes ist bei kleinen
Stichprobengrößen ein schlechter Indikator für die Anpassungsgüte.
Zusammenhang zwischen adjustiertem Bestimmtheitsmaß, F-Test und t-Test
Direkt aus der obigen Definition von
folgt
.
Wenn man diesen Ausdruck nun nach
auflöst ergibt sich
.
Analog dazu gilt für das adjustierte Bestimmtheitsmaß des Nullhypothesenmodells,
welches nur
erklärende Variablen besitzt
.
Bei einsetzen der beiden Größen in den F-Wert
.
ergibt sich durch algebraische Umformungen
.
Als Folge daraus ist der F-Wert genau dann größer als ,
wenn
.
Durch Umstellen erhält man
.
Diese Ungleichung ist genau dann erfüllt, wenn .
Anders ausgedrückt übersteigt das adjustierte Bestimmtheitsmaß des
unrestringiertes Modells das adjustierte Bestimmtheitsmaß des restringierten
Modells genau dann wenn der F-Wert des F-Tests größer als
ist. Der t-Test stellt einen Spezialfall des F-Tests dar. Er
ergibt sich im Fall einer Restriktion
.
Für die Teststatistik eines solchen Tests gilt, dass die quadrierte
t-Statistik der F-Statistik entspricht
.
Die obige Ungleichung ist für einen t-Test ebenso erfüllt, genau dann
wenn
.
Verallgemeinerung mittels Zielfunktion
Ein weiterer Ansatz stellt die Verallgemeinerung des Bestimmtheitsmaßes
mittels einer anderen Zielfunktionen
als die Residuenquadratsumme dar. Sei
die Zielfunktion, die es zu maximieren gilt,
stellt den Wert in einem Leermodell
dar,
bezeichnet den Wert im angepassten Modell, und
bezeichnet den größtmöglichen Wert von
.
Der maximale potentielle Zuwachs in der Zielfunktion, der durch die Hinzunahme
von erklärenden Variablen resultiert ist
.
Im Gegensatz dazu stellt der gegenwärtige Zuwachs
dar. Die Verallgemeinerung des Bestimmtheitsmaßes mittels Zielfunktionen ergibt
sich dann durch
.
Hier bei bedeutet das Subskript
„relativer Zuwachs“. Bei der Kleinste-Quadrate-Schätzung ist die maximierte
Verlustfunktion
.
Dann ist
,
und
,
und somit gilt für das Bestimmtheitsmaß bei der Kleinste-Quadrate-Schätzung
.
Die Vorteile dieser Verallgemeinerung mittels Zielfunktionen sind, dass das Maß
zwischen Null und Eins liegt und steigt, wenn weitere erklärende Variablen dem
Modell hinzugefügt werden. Wenn
(dies ist beispielsweise bei binären
diskreten Entscheidungsmodellen und multinomialen Modellen der Fall), dann
ergibt sich die verwandte Maßzahl
.
Pseudo-Bestimmtheitsmaß
Im Falle einer linearen
Regression mit einer abhängigen metrischen Variablen
wird die Varianz dieser Variablen benutzt um die Güte des Regressionsmodells zu
beschreiben. Bei einem nominalen
oder ordinalen Skalenniveau von
existiert jedoch kein Äquivalent, da man die Varianz und damit ein
Bestimmtheitsmaß nicht berechnen kann. Für diese wurden verschiedene
Pseudo-Bestimmtheitsmaße vorgeschlagen, beispielsweise Maße die auf der
logarithmischen
Plausibilitätsfunktion (log-Likelihood-Funktion) basieren, wie
z.B. das Pseudo-Bestimmtheitsmaß nach McFadden
(für eine Erläuterung der Notation siehe Maße die auf der logarithmischen Plausibilitätsfunktion basieren).
Bei nichtlinearen Modellen werden Pseudo-Bestimmtheitsmaße verwendet. Allerdings gibt es kein universelles Pseudo-Bestimmtheitsmaß. Je nach Kontext müssen andere Pseudo-Bestimmtheitsmaße herangezogen werden.
Prognose-Bestimmtheitsmaß
Während das Bestimmtheitsmaß, das adjustierte Bestimmtheitsmaß oder auch die Pseudo-Bestimmtheitsmaße eine Aussage über die Modellgüte machen, zielt das Prognose-Bestimmtheitsmaß auf die Vorhersagequalität des Modells. Im Allgemeinen wird das Prognose-Bestimmtheitsmaß kleiner als das Bestimmtheitsmaß sein.
Zunächst wird der Wert des PRESS-Kriteriums, also die prädiktive Residuenquadratsumme (engl.: predictive residual error sum of squares) berechnet
.
Hierbei ist
der beobachtete Wert und
der Wert, der sich als Schätzung von
ergibt, wenn alle Beobachtungen außer der
-ten
in das Regressionsmodell einfließen. Zur Berechnung des der prädiktiven
Residuenquadratsumme müssten daher
lineare Regressionsmodelle mit jeweils
Beobachtungen berechnet werden.
Es lässt sich jedoch zeigen, dass das Residuum
aus den „gewöhnlichen Residuen“
(bei Benutzung aller
Beobachtungen) berechnet werden kann. Das Prognose-Bestimmtheitsmaß ergibt sich
dann als
.
Mehrgleichungsmodelle
Für Mehrgleichungsmodelle lässt sich ein Bestimmtheitsmaß wie folgt definieren:
,
wobei
die Residuenquadratsumme der durchführbaren
verallgemeinerten KQ-Schätzung ist und
für
steht im Fall, dass
nur aus einem Absolutglied besteht.
Bestimmtheitsmaß in R
Als einfaches Beispiel zur Berechnung des Bestimmtheitsmaßes in R wird zunächst der Korrelationskoeffizient zweier Datenreihen berechnet:
# Groesse wird als numerischer Vektor
# durch den Zuweisungsoperator "<-" definiert:
Groesse <- c(176, 166, 172, 184, 179, 170, 176)
# Gewicht wird als numerischer Vektor definiert:
Gewicht <- c(65, 55, 67, 82, 75, 65, 75)
# Berechnung des Bravais-Pearson-Korrelationskoeffizient mit der Funktion "cor":
cor(Gewicht, Groesse, method = "pearson")
Anschließend wird, um das Bestimmtheitsmaß zu erhalten, der Bravais-Pearson-Korrelationskoeffizient quadriert:
# Das Bestimmtheitsmaß ist bei einer erklärenden Variablen das Quadrat des Korrelationskoeffizienten "cor":
cor(Gewicht, Groesse, method = "pearson")^2
# Bei Ausführung ergibt sich ein ''R''-Quadrat-Wert von 0,864, d. h. 86,40 % der Streuung im Körpergewicht kann durch die lineare Regression von Körpergewicht auf Körpergröße erklärt werden.
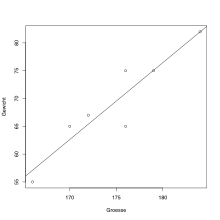
Mithilfe der Statistiksoftware R kann eine einfache lineare Regression durchgeführt werden. Dies kann in R durch die Funktion lm ausgeführt werden, wobei die abhängige Variable von den unabhängigen Variablen durch die Tilde getrennt wird. Die Funktion summary gibt die Koeffizienten der Regression und weitere Statistiken, wie z.B. das adjustierte Bestimmtheitsmaß, hierzu aus:
# Lineare Regression mit Gewicht als Zielvariable
# Ergebnis wird als reg gespeichert:
reg <- lm(Gewicht ~ Groesse)
# Ausgabe der Ergebnisse der obigen linearen Regression:
summary(reg)
Literatur
- Ludwig Fahrmeir, Thomas Kneib, Stefan Lang: Regression: Modelle, Methoden und Anwendungen.. Auflage. Springer Verlag, 2009, ISBN 978-3-642-01836-7.
- J. Neter, M. H. Kutner, C.J. Nachtsheim, W. Wasserman: Applied linear statistical models. 4. Auflage. McGraw-Hill 1996.
- M.-W. Stoetzer: Regressionsanalyse in der empirischen Wirtschafts- und Sozialforschung – Eine nichtmathematische Einführung mit SPSS und Stata. Berlin 2017, ISBN 978-3-662-53823-4.
Anmerkungen
- ↑
Die durch die Kleinste-Quadrate-Schätzung
gewonnenen Parameterschätzer
und
werden oft auch als
und
notiert.
- ↑
Es gibt in der Literatur keinen Konsens
hinsichtlich der Abkürzungen
,
und
. Die „totale Quadratsumme“ (sum of squares total) wird oft statt
auch als
abgekürzt. Unglücklicherweise wird die „durch die Regression erklärte Quadratsumme“ (sum of squares explained), hier abgekürzt als
, manchmal als „Quadratsumme der Regression“ (sum of squares regression) bezeichnet und damit als
abgekürzt. Wenn dieser Ausdruck jedoch mit seiner natürlichen Abkürzung
abgekürzt wird, kann er leicht mit der „Residuenquadratsumme“ (sum of squares residual) verwechselt werden, die ebenfalls mit
abgekürzt wird. Manche statistischen Programmpakete bezeichnen die „erklärte Quadratsumme“ (sum of squares explained) auch als „Modellquadratsumme“ (sum of squares model). Die Abkürzungsproblematik wird dadurch verschärft, dass die „Residuenquadratsumme“ oft auch als „Fehlerquadratsumme“ (sum of squares errors) bezeichnet wird (diese Bezeichnung ist besonders irreführend, da Störgrößen bzw. Fehler und Residuen unterschiedliche Größen sind).
- ↑ Der Begriff Bestimmtheitsmaß ist eine Komposition aus den beiden Grundbegriffen der philosophischen Logik: Bestimmtheit und Maß. Der Begriff der (inneren) Bestimmtheit bezeichnet in der philosophischen Logik die „Qualität“ bzw. „Güte“ eines Dings und das Maß eine „qualitative Quantität“.
- ↑ Zur Vereinfachung werden im Artikel bei allgemeinen Definitionen die Summationsgrenzen weggelassen.
- ↑ Die Bezeichnung Streuungszerlegung charakterisiert das Wesen, aber nicht den mathematischen Vorgang, indem nicht die Streuung, sondern die totale Quadratsumme zerlegt wird.
- ↑
Dies gilt, wegen
.
- ↑
Im Allgemeinen ist der Standardfehler der
Regression gegeben durch
.
- ↑
Bestimmung der Funktion auf Grundlage der
verwendeten Abbildung, Prof. Engelbert Niehaus (Uni Koblenz) – Koeffizienten und
Typ der Abbildung wurden aus dem Diagramm abgelesen, um Abbildung und
Funktionsterm konsistent zu halten. Bestimmung der Koeffizienten von dem
Funktionsterm
erfolgte, um die nebenstehende Abbildung nicht verändern zu müssen.
- ↑
Bestimmung der quadratischen Funktion auf
Grundlage der verwendeten Abbildung, Prof. Engelbert Niehaus (Uni Koblenz) –
Koeffizienten und Typ der Abbildung wurden aus dem Diagramm abgelesen, um
Abbildung und Funktionsterm konsistent zu halten. Bestimmung der Koeffizienten
von dem Funktionsterm
erfolgte, um die nebenstehende Abbildung nicht verändern zu müssen.
- ↑ Für Populationsgrößen werden konventionell griechische Buchstaben und für Stichprobengrößen lateinische Buchstaben verwendet.
- ↑
Die wahre Kovarianzmatrix kann in Anwendungen
nicht berechnet werden, da die Varianz der Störgrößen
unbekannt ist.
- ↑
Mit
ist die Verteilung der Teststatistik unter der Nullhypothese gemeint.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.09. 2025